基于分层强化学习的无人机空战多维决策

张建东,王鼎涵,杨啟明,史国庆,陆屹,张耀中

(1.西北工业大学 电子信息学院,陕西 西安 710072;2.沈阳飞机设计研究所,辽宁 沈阳 110035)

0 引言

现代空战以决策速度快、机动性能高、态势感知能力强、高鲁棒性等特点为核心,然而有人机受人类生理极限限制,无法发挥出战斗机的极限性能。无人机摆脱了人类生理极限,但机动控制由地面指挥,决策速度慢,若大幅延长观察、判断、决策、行动(OODA)环的时间则容易错失战机,因此智能化无人机空战自主决策成为当今的研究热点。

随着OODA 3.0概念的提出[1]以及人工智能技术的不断发展,无人机在机动决策等单一维度的决策方面已经实现了一定程度的自主化,并且在某些方面已经达到或者超越了人类飞行员的水平。然而,空战过程是一个复杂的多维决策过程,要完成空战的自主化决策,必须要实现多个维度的协同自主化决策。因此无人机多维空战决策一直是该领域亟需攻克的难关,其对实现完全无人化空战的终极目标至关重要。

当前对无人机自主决策的诸多研究都集中在机动决策方面,通过深度Q网络(DQN)[2]、深度确定性策略梯度(DDPG)[3-5]、Actor-Critic等深度强化学习算法来实现对无人机的机动控制。但这些方法有着超参数敏感、策略选择单一、无法解决多维决策问题[6]等缺点,无法很好地满足无人机空战对于快速收敛、高鲁棒性及多维决策的要求。事实上,空战决策除了机动决策外,还包括传感器决策、武器决策、干扰决策等各方面多维度的决策。相比而言,分层强化学习凭借着其能够进行空间分解和分层训练的优势,有望使无人机具备充足的策略,从而完成复杂的作战任务。

目前,已经有很多学者使用分层强化学习方法对无人机多维决策的相关问题进行了探索性研究。王俊敏等[7]在空战编队协同上应用了分层策略,但关键的观测数据并未给出,无法进行有效训练。付跃文等[8]应用了分层优化方法解决了无人机之间协作任务规划模块设计,证实了空战决策空间建模的可行性。文永明等[9]研究了一种无人机机群对抗多耦合任务智能决策方法,采用分层强化策略训练方法,提出混合式深度强化学习架构,完成了无人机突防侦察任务及目标的协同分配任务,证实了分层架构的有效性。程先峰等[10]采用一种基于MAXQ的Multi-agent分层强化学习的无人机协调方法,增强了无人机在混合运行复杂环境下适应环境和自协调的能力。吴宜珈等[11]提出基于选项的近端策略分层优化算法,用来解决近端策略优化算法在空战智能决策过程中面临的动作空间过大、难以收敛的问题。通过对相关文献的分析可以看出,目前在无人机多维决策方面的研究还不够完善,所研究问题的规模都比较小,决策维度与现实差距较大,导致其应用环境过于简单。

与此同时,以美国为代表的军事强国正在紧锣密鼓地开展将人工智能技术应用于无人机复杂作战任务的相关实验验证。2021年美国洛克希德·马丁公司于美国国防部高级研究计划局(DARPA)举办的Alpha狗斗(ADT)比赛中展示了其最新研发的分层强化学习算法适应性新颖策略生成的操作层级结构(PHANG-MAN[12]),成功地将分层强化学习方法应用到无人机空战决策中,实现了多维空战决策中的追击决策、规避决策、打击决策。该算法在ADT决赛中斩获第二,并击败了美国空军F-16武器教练课的毕业生。该算法充分体现了分层强化学习在解决多维空战决策问题中的策略模块化、智能化、去中心化的特点,这一实验结果表明美军在无人机多维决策方面已经达到了很高水平。此外,其他相关研究[13-21]均表明深度强化学习在空战中的理论可行性。因此,进行无人机多维自主决策的应用研究具有一定的理论意义和使用价值。

本文以无人机一对一(1v1)、集群四对四(4v4)的红蓝空战对抗任务为场景,基于分层强化学习的架构建立无人机智能空战的多维决策模型,采用Soft Actor-Critic算法训练底层单元策略,并结合专家经验建立元策略组,扩展了决策的维度。改进传统的Option-Critic算法,设计优化了策略终止函数,提高了策略切换的灵活性,实现了空战中多个维度决策的无缝切换。

为了较好地完成目标打击任务,设计雷达开关、主动干扰、队形转换、目标探测、目标追踪、干扰规避、武器选择与目标打击共7种元策略。以贪心算法作为顶层元策略选择策略,完成智能多维空战自主决策。仿真实验结果表明,训练完成后的无人机可以灵活地完成元策略的切换调用,能够以丰富的元策略组合完成更高层次的作战决策,体现了分层强化学习算法在提升无人机自主决策维度上的应用潜力。

1 空战决策维度分解

根据空战OODA环的概念,第1步需要确定目标方位。本文设定双方雷达探测能力一致,为实现先敌发现,需要构建高效的搜索方法。

贯穿整个空战过程的雷达探测至关重要,它有着确定目标精确方位、攻击引导的作用。在打击前,应确保目标不丢失,因此需要我机雷达能够持续照射目标,同时规避目标的电磁干扰。

在目标探测过程中,被动雷达能够在电磁静默情况下确定目标方位。然而单架飞机的被动探测仅能确定目标方向,无法精确确定目标的坐标。若要完成精确探测,则需要至少两架飞机协同探测。

为降低因雷达开机暴露位置的风险,需要对雷达资源做合理的分配。在编队内,对于距离较近、航向差较小的我机,仅需开启其中一个雷达,因此需要给出合理分配雷达资源的数学模型和规则模型。

在打击目标前,需要判断目标的距离以及自身剩余的导弹数量和种类以选择合适的导弹类型。打击目标时,应该确保我机安全,采用合理的干扰策略,避免暴露位置。

在多机作战过程中,编队往往能够最大化作战能力,最小化作战损耗。常用的编队模型为长机-僚机编队。作战伊始通过合理的编队布局增强战力,作战过程中遇到队形破坏可以采用队形转变策略重组编队,维持整个作战过程中的战力。

综上所述,整个空战流程涵盖了雷达开关、主动干扰、队形转换、目标探测、武器选择、目标打击、目标追踪、干扰规避策略,空战中的主要决策环节如图1所示。

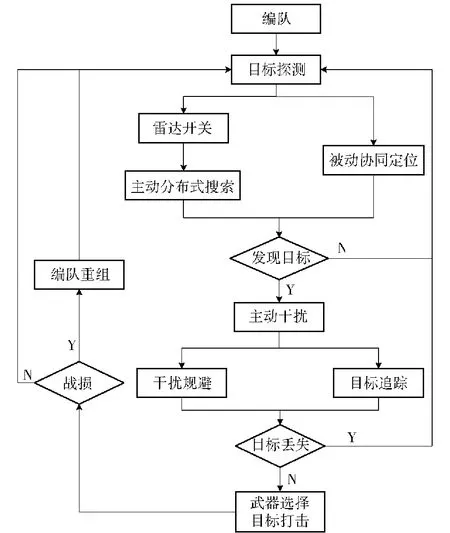
图1 空战全流程分析Fig.1 Analysis of the whole air combat process

1.1 雷达开关策略模型

为了降低因雷达开机暴露位置的风险,飞机往往会在非必要时刻关闭雷达,处于电磁静默状态。本文构建了雷达开关模型,分析探测重叠区域,给出了雷达开关判定规则。

为避免探测资源浪费,并降低暴露位置风险,分析了雷达探测重叠区域,如图2所示。图2中,θ表示雷达的探测半角,λ1和λ2分别表示两架飞机的航向角。

图2 雷达探测重叠区域分析Fig.2 Overlapping area analysis of radar detection

设d表示两机的间距,则无人机进入判决区域的条件如式(1)所示：

(1)

式中：r为雷达探测距离。

式(1)表述了两机间距及两机航向角度差值小于阈值时,两机处于判决区域,需要关闭其中一架飞机的雷达。

设定判决状态变量p,如果满足判决公式,则判决变量p置为1,否则置为0,具体的判定规则如下：

1)若p=1,则关联判决友机编号(id)为ip,本机id为im,根据全局判定列表[(p,ip,im)…],观察是否存在重复ip,若存在则不开启im=ip飞机的雷达,开启ip≠im飞机的雷达。否则开启长机雷达。

2)所有不在全局列表中的无人机全部开启雷达。

模型输入为我机的坐标、航向、雷达开关状态,输出为雷达的开机频点,0表示关机,非0表示开机相应频点。

1.2 主动干扰策略模型

为了实现瞄准式干扰,本文构建了主动干扰模型,分析了干扰区域,给出了干扰规则。

实施干扰前,我机需要确定被干扰目标的雷达频点,记为rt。若目标处于我机主动雷达的照射范围内且不受目标干扰时,则我机可以获取到目标雷达开机频点的观测信息。此时仅需将我机的干扰频点rj设置为目标的雷达频点即可完成瞄准式干扰,即满足：

rt=rj

(2)

模型的输入为目标的开机频点,未探测到时奖励记为0,探测到n个目标干扰频点,奖励记为n。输出为我机的开机频点。

1.3 队形转换策略模型

为了提高协同效能,构建队形转换模型,建立长机-僚机编队模型,考虑到作战过程中被破坏的情况给出了编队重组方案。

初始时刻我方编队为两两一组,以长机-僚机形式编队,长机执行搜索-攻击任务,僚机进行探测干扰任务,掩护长机。若长机被击毁,僚机将接替长机位置完成攻击与目标探测等任务。长机id记为idl,僚机id记为idf。构建编队列表与全局编队{[idl,idf]…},若作战过程中因战损导致编队结构被破坏,则可以通过判断编队列表进行编队重组。例如,编队1长机被击毁,记[-idl,idf]。若整队成员全部被击毁,则将该编队列表移出全局编队。

编队重组通过遍历所有编队,根据编队列表中是否存在负值筛选不完整编队,不完整编队数量记作N,重组编队数记作T,有

T=N%2

(3)

无法重组编队数记为L,有

L=N-2T

(4)

重组的编队根据遍历顺序赋予长机或僚机职能,无法重组的单机单独完成作战任务。

模型的输入为我机编队的位置坐标、航向及我机的存活状态,输出为我机的航向。

1.4 目标探测策略模型

为实现目标的快速定位,本文构建目标探测模型,提出基于人工势场的主动搜索方法,构建搜索圆域模型,设计被动搜索方案。

为确保主动搜索时编队的分布式搜索,采用人工势场维持我方无人机之间的距离,主要采用人工势场中的斥力场,我机编队在分布式搜索过程中应避免搜索区域的重复。通过定义势场函数,当友机间距离过近时,势场的斥力趋近无穷;当友机间距离超过指定值时,势场的斥力减少到0 N。定义ρ(q)为我机到其他友机自定义可调圆形边界QO的距离：

(5)

式中：q为我机当前位形;q′为边界位形;∂QO表示空间障碍区域的边界。定义ρ0为一个障碍物影响的距离,当我机q距离障碍(即友机)距离大于ρ0时,不会排斥q。符合上述标准的势函数描述为

(6)

式中：η为比例系数。排斥力为Urep(q)的负梯度,当ρ(q)≤ρ0时,排斥力为

(7)

如果QO为凸函数,b是QO边界上最接近q的点,则

ρ(q)=‖q-b‖

(8)

其梯度为

(9)

被动探测方面,被动雷达通过吸收敌方电磁波照射获取目标相对于自身的方位。被动探测的优点是能够在不发射电磁波的情况下对目标进行探测,缺点是精度较差,单架飞机仅能测得辐射来源的粗略方向,需要至少两架无人机协同被动探测目标才能实现目标位置的准确计算。

多机协同作战可利用被动雷达定位目标位置,当编队内有我机被动接收到目标信号时,友机配合支援,从不同方向进行同步雷达搜索,可以快速定位目标,并进行打击(干扰,打击协同一体化),但前提是目标不丢失。目标丢失分两种情况：

1)目标被其他友机摧毁;

2)目标雷达照射区域脱离被动探测区域(例如突然改变方向等)。

针对第1种情况,可以通过设计并检查全局摧毁列表来解决;针对第2种情况,放弃被动探测方法,直接开启主动雷达搜寻目标。

具体的搜索方法为：我机1被动探测到目标,主动雷达并没有探测到;我机1根据自身坐标位置及航向确定假想目标最远位置(被动探测能够确定目标方向,因此可以确定目标在该方位线上最远距离dmax到最近距离dmin之间),第1次记录的点记为pv(xv,yv),此时调动距离最近的友机前来支援,但是最近的友机也可能受到目标的干扰,此时应跟随我机1一同朝向目标行进,并调动其他距离最近的友机。如果在判断圆域外,直接向pv点航行(在中轴线友机侧),或者向我机1所在的位置航行(在中轴线友机另一侧)。如图3所示,友机在我机同侧时朝向pv航行,友机雷达探测区域将覆盖目标位置,进而探测到目标具体坐标及方位;友机在我机对侧时朝我机(我机1)方向航行,同样可以覆盖目标所有可能的位置。

图3 我机位于判断圆域外分析图Fig.3 Analysis of our UAVs located outside the judgment circle

如果在判断圆域内且位于我机1一侧,同样直接朝向pv航行,到达中线位置仍未探测到,则掉头朝向我机1航行。反之亦然,按照该策略一定能够快速探测到目标。图4中深蓝色扇形表明初始位置友机的探测区域,由于目标处于探测区域外,为了全覆盖对侧目标可能存在的区域,需要飞到中线,如果没有探测到,折返朝向我机1航行。

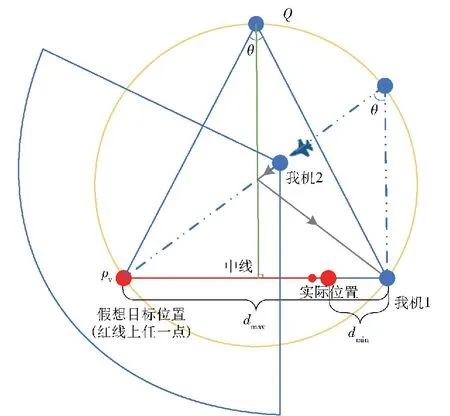
图4 我机位于判断圆域内分析图Fig.4 Analysis of our UAVs located in the judgment circle

已知θ=60°,我机2飞行到中线再折返的原因在于中线与判断圆域的交点Q距离pv恰好为最大探测距离dmax,此时朝向pv能够覆盖目标所在弦。若我机2在圆域内Q点与我机1构成的弦内接以pv为圆心、pvQ为半径的部分圆弧,在此圆弧外时距离pv大于最大探测距离dmax,需要飞到中线附近才能够全覆盖。这个极限在于Q点,越趋近于Q点,意味着越需要朝着中线行进,才能全覆盖。为了便于处理,我机2没有在弦的不同侧采取不同策略,而是统一按照先到达中线再折返这一思路。实际上,当我机2在圆域内由Q点与我机1构成的弦右侧圆弧内时,只需朝向pv进行瞬时探测,若没有发现目标即可折返。

模型输入为我机的位置坐标及航向,输出为我机的航向。

1.5 武器选择与目标打击策略模型

为实现先敌打击,构建武器选择与目标打击模型,建立打击目标分配策略,分析导弹攻击区,给出打击策略。导弹攻击区如图5所示。

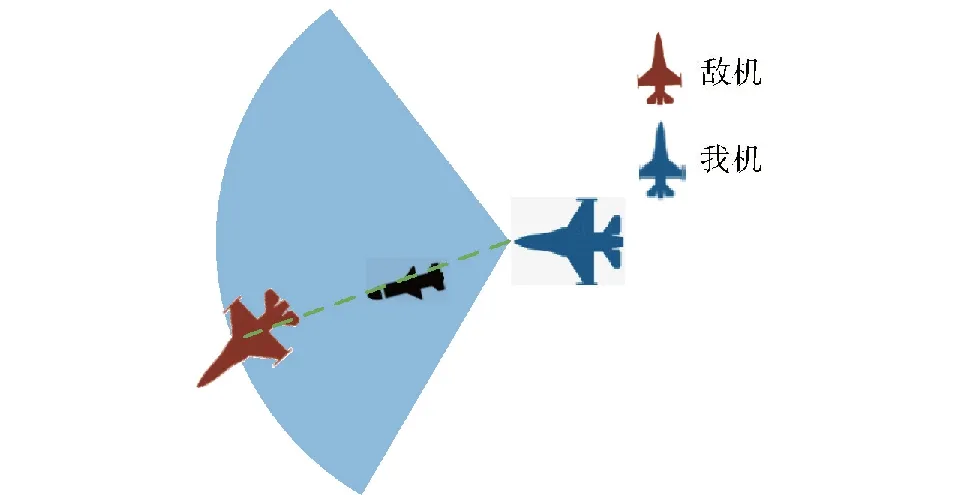
图5 导弹攻击区Fig.5 Missile attack zone

整个作战OODA环中先敌打击至关重要。显然,当目标位于武器极限攻击距离时立即开火即为最优打击策略。武器的种类需要根据距离进行选择,首选远程导弹,远距探测到即打击,无远距导弹可贴近用中距导弹,近距离则选中距导弹。

此外,当编队作战时,应考虑打击目标的分配问题。打击目标id放入全局打击列表中,每次迭代到相应无人机时查询本机打击列表是否在全局打击列表中,若存在,则具有相同打击目标的无人机不打击此目标。若打击无人机阵亡,则将目标id从全局打击列表中移除。打击目标按照我机与目标个体间距离大小进行分配,距离近的个体优先执行对应id的目标打击任务,如果目标在全局打击列表中,友机选择除此机之外探测到的目标进行打击。

模型输入为探测到的目标位置坐标及航向,输出为我机的航向。

1.6 目标追踪策略模型

为实现探测到目标后的目标追踪,本文构建目标追踪模型,构建其观测值与奖励函数,最后基于最大化熵软演员-评论家(SAC)算法训练模型。

模型输入为我机位置坐标、航向及探测到的目标位置坐标,输出为我机航向。

1.7 干扰规避策略模型

为了避免追踪过程中因目标干扰导致目标丢失,本文构建了干扰规避模型,构建其观测值与奖励函数,最后基于SAC算法训练模型。

模型输入为我机的位置坐标、探测到的目标位置坐标及我机航向,输出为我机的航向。

2 空战多维决策模型

为实现空战多维决策,需要构建空战多维决策模型。本文基于分层结构,将底层决策模型分为依靠专家知识的经验模型和基于SAC算法决策的训练模型。针对决策模型何时结束的问题,本文基于Option-Critic算法,摒弃策略训练,取而代之使用已有的策略模型,仅训练策略的终止函数,实现策略的灵活切换。顶层策略选择器基于贪心算法,选择期望回报最高的策略作为当前状态下的决策。

2.1 元策略模型训练算法

对于由雷达开关、主动干扰、队形转换、目标探测、武器选择与目标打击元策略构成的经验模型基于专家知识无需训练。对于由目标追踪和干扰规避策略构成的训练模型,训练采用SAC算法。其在传统的Actor-Critic方法引入最大化熵的思想,采用与PPO[19]类似的随机分布式策略函数,且是Off-Policy、Actor-Critic的算法。SAC算法区别于其他算法的明显之处在于SAC同时最大化了回报和策略的熵值。在实际应用中,SAC在各种常用的benchmark以及真实的机器人控制任务中表现稳定、性能优秀,具有极强的抗干扰能力。针对 DDPG算法选择确定性策略问题,SAC引入了最大化熵方法,能够让策略尽可能随机,智能体可以充分探索状态空间,避免策略过早陷入局部最优,并且可以探索到多个可行的方案来完成制定任务,提高了抗干扰能力。此外,为提高算法性能,采用DQN中的技巧,引入两个Q网络以及目标网络,为表述最大化熵值的重要程度,引入自适应温度系数α,针对不同问题温度系数的调节,将其构造成一个带约束的优化问题,即最大化期望收益的同时,保持策略的熵大于一个阈值。SAC训练模型算法的伪代码如图6所示。

图6 SAC训练模型算法伪代码Fig.6 Pseudocode of SAC training model algorithm

2.2 空战多维决策算法

2.2.1 决策结构分解

为构建整体作战策略,需要确定作战流程以及作战逻辑,整体作战的分层决策结构图如图7 所示。

图7 整体作战的分层决策结构Fig.7 Hierarchical decision-making structure for operations

决策选择层作为策略选择器负责在当前状态下进行元策略的挑选,初始编队及需要编队重组时选择队形转换策略;在雷达未发现目标阶段应选择目标探测策略进行目标搜索(分布式);搜索过程中要合理分配雷达资源选择雷达开关策略;发现目标选择目标追踪策略对目标展开追击,追踪目标过程中避免目标丢失与反击应该采取主动干扰策略对目标雷达干扰,并采取干扰规避策略;目标进入攻击区时采用武器选择与目标打击模型完成对敌打击。

整个作战策略由7部分元策略构成：训练和干扰规避2个训练策略;雷达开关、主动干扰、队形转换、目标探测及武器选择与目标打击5个固定策略。对于训练策略基于Actor-Critic框架分别构建执行和评估神经网络。记录状态空间、动作空间和奖励值,最终为这两个策略设计经验池。

2.2.2 改进Option-Critic方法

由于基于传统Option-Critic的分层强化学习方法很难引入专家的经验知识且只能输入元策略的个数,其余均由Option-Critic算法训练每个元策略的策略函数和终止函数。而选项方法虽能引入经验知识,但要求人为设计终止函数,无法实现元策略的灵活切换。为了更好解决复杂空战问题,引入现有效果较好的专家经验模型十分必要,且具有明显的策略含义。本文基于传统的Option-Critic算法并做出改进,为引入自定义模型,首先为Option-Critic指定现有元策略模型的个数,将每个自定义策略模型和Option-Critic框架下的模型一一对应起来,在执行Option-Critic框架训练时,对于选中的策略仅训练其终止函数,策略函数由自定义模型提供。

上层策略选择一个选项ω∈Ω,选项包含3部分：策略πω(a|s)表示选项中的策略,终止条件β表示状态s有βω(s)概率结束当前选项,初始集Iω表示选项的初始状态集合。

当终止函数返回0时,下一步还会由当前选项来控制;当终止函数返回1时,该选项的任务暂时完成,控制权交还给上层策略。把每个选项的终止函数都用神经网络进行函数近似来参数化表示,即βω,ϑ(s),ϑ表示网络参数,策略选取构建好的模型策略πω(a|s)。在这些选项之间做选择的上层策略,用πΩ(ω|s)表示,即在状态s时策略选择选项ω的概率。在此基础上,可以定义某状态下选择某个选项后产生的总收益。选择某个选项时,采取某行动之后产生的总收益和在使用某选项到达某状态之后产生的总收益。

选项内部仅更新为各选项的终止函数βω,ϑ(s)。根据总折扣回报相对其参数的导数,可以利用如policy gradient的方法更新其参数。改进的Option-Critic算法结构如图8所示,与原算法相比,本文将训练策略改成了自定义策略。图8中,AΩ为选项之间的优势函数,at为t时刻的动作,ωt为t时刻选择的选项,rt为t时刻的奖励,QU为最优选项-价值函数。

图8 改进Option-Critic算法结构图Fig.8 Diagram of improved Option-Critic algorithm structure

2.2.3 多维空战决策算法构建

(10)

式中：γ为折扣率;st为t时刻状态;ω、a为尚未观测到的随机变量。

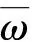
图9 Beta算法伪代码Fig.9 Pseudocode of Beta algorithm

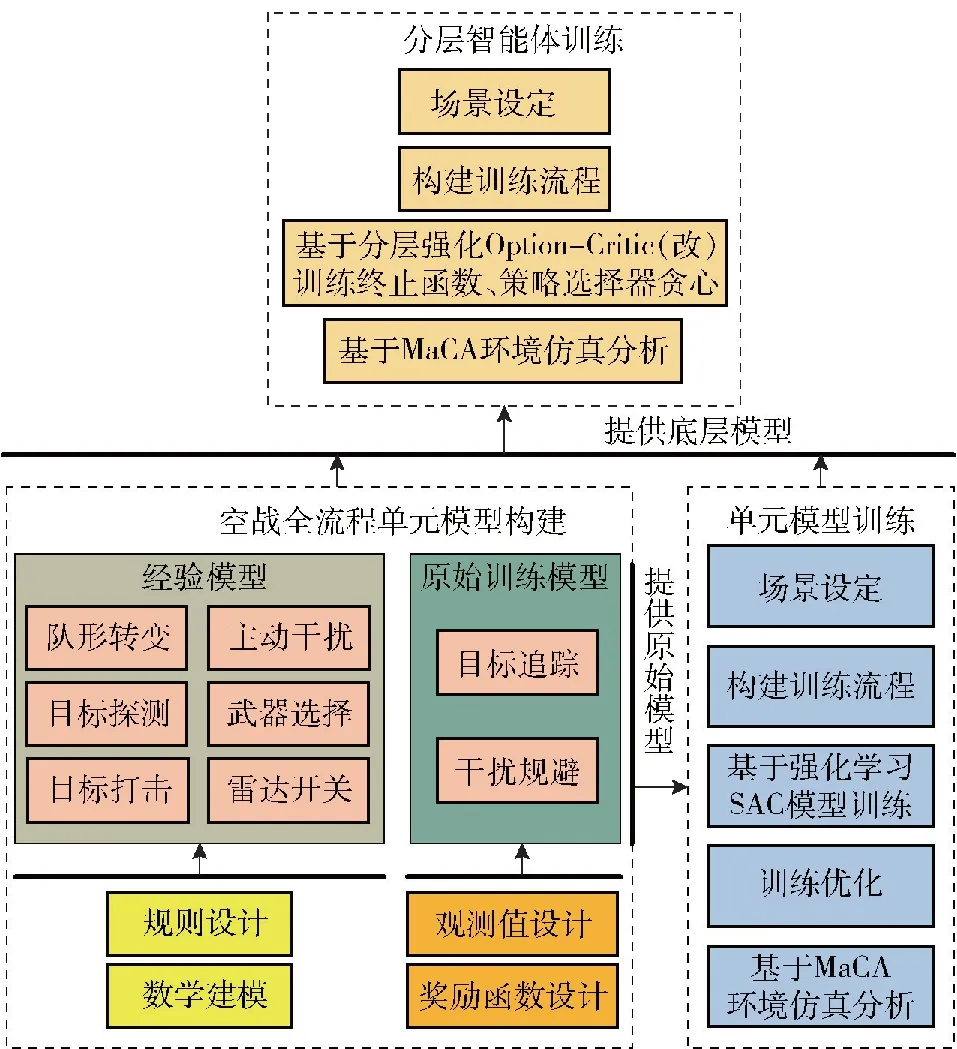
图10 多维空战的构建方法及流程Fig.10 Construction method and process of multi-dimensional air combat

3 仿真环境与仿真结果

3.1 实验环境设定

3.1.1 软件平台

选用文献[22]推出的MaCA环境对本文建立的模型进行仿真验证。MaCA环境支持作战场景和规模自定义,智能体数量和种类自定义,智能体特征和属性自定义,支持智能体行为回报规则和回报值自定义等。

MaCA环境中提供了一个电磁空间对抗的多智能体实验环境,环境中预设了探测单元和攻击单元两种智能体类型：探测单元可模拟L、S波段雷达进行全向探测,支持多频点切换;攻击单元具备侦察、探测、干扰、打击等功能,可模拟X波段雷达进行指向性探测,模拟L、S、X频段干扰设备进行阻塞式和瞄准式电子干扰,支持多频点切换,攻击单元还可对对方智能体进行导弹攻击,同时具有无源侦测能力,可模拟多站无源协同定位和辐射源特征识别。

MaCA环境为研究利用人工智能方法解决大规模多智能体分布式对抗问题提供了很好的支撑,专门面向多智能体深度强化学习开放了RL-API接口。环境支持使用Python语言进行算法实现,并可调用Tensorflow、Pytorch等常用深度学习框架。

3.1.2 硬件环境

CPU采用Intel i7-10700KF,GPU采用Nvidia RTX 3070加速深度神经网络训练过程,显存大小为8 GB,内存16 GB。

3.2 定义想定任务

假定红蓝双方功能完全一致。双方在指定地图大小的二维环境中完成整个探测-干扰-规避-协同-打击作战流程。蓝方为规则驱动,规则未知。双方任务为在规定作战步数内尽可能少地消耗导弹去歼灭更多的目标,取得数量优势。单机1v1对抗场景地图修改双方战机数量为1,远程导弹与近程导弹各4发,地图尺寸设置为500×500。目标开启阻塞干扰,算法采用MaCA环境中的fix_rule_no_att黑盒算法;我机采用多维决策算法。共执行20回合,每回合最大运行步数为5 000。

多机4v4对抗场景地图修改双方战机数量为4,远程导弹与近程导弹各4发,地图尺寸设置为500×500。目标开启阻塞干扰雷达,算法采用MaCA环境中的fix_rule_no_att黑盒算法;我机采用Beta算法。共执行10回合,每回合最大运行步数为5 000。

3.3 跟踪元策略训练

3.3.1 训练方法

我机当前状态下的航向角为α1,坐标为(x0,y0);目标当前状态下的方位角为α2,坐标为(x1,y1)。记下一个状态我机航向角为α1n,坐标为(x0n,y0n);下个状态目标方位角为α2n,坐标为(x1n,x2n),设偏航角为下个状态我机航向角与当前状态目标方位角的差值,记作Δ,有Δ=α1n-α2。目标追踪模型为纯追踪,问题模型为最小化Δ。Δ和α2作为神经网络的输入观测值。目标追踪问题模型最小化Δ,因此可以构造二次函数R=-Δ2作为问题的奖励函数,Δ越小,奖励值越大,越接近0。

随机初始状态,我机开启雷达对目标进行探测,目标干扰雷达关闭。训练环境采取1v1方式,首先固定我机进行跟踪训练。双方观测规则均采用MaCA环境中的raw规则,输入状态维度为2,动作维度为1,Actor-Critic网络中Actor策略网络学习率设置为3×10-4,Critic策略网络学习率设置为3×10-3,温度参数设置为3×10-4,神经网络隐含层单元数为512,共两层。回报折扣率设为0.99,软更新参数设置为0.005。经验池大小设置为100 000,最小存储数据量设为1 000条。一次喂入神经网络的batch大小为64,总回合数为100,每回合最大步数设置为500。将环境Render设置为可见。

为了加快训练并丰富样本,提出了训练优化方法。设置目标高速移动,我机固定,设置目标移动策略为每隔10步随机改变航向,缩小地图尺寸为50×50。频繁的方位改变能够让我机充分探索各个航向。

整体训练过程收敛迅速,通过观察可见我机成功锁定目标,如图11所示。

图11 目标运动、我机固定时的追踪训练示意图Fig.11 Schematic diagram of tracking training when the enemy UAVs are moving and our UAV is fixed

图12和图13展示了总训练轮数为100和1 000次的回报曲线,可见,使用SAC算法在目标运动,我机固定时的环境下训练效果显著,该目标追踪问题在每回合1 000步的迭代中能够在第10回合左右达到收敛,收敛效果很好。

图12 SAC跟踪训练的原始回报曲线(100轮)Fig.12 Original reward curve of SAC tracking training (100 rounds)

图13 SAC跟踪训练的原始回报曲线(1 000轮)Fig.13 Original reward curve of SAC tracking training (1 000 rounds)

在1 000次的训练中,为了避免过拟合问题,丰富训练样本,本文采用了动态改变环境的方法,通过动态改变地图的大小与无人机位置保证初识状态的不同。从图13中可见,算法收敛后仍有一些回合回报值较低,但很快便达到收敛状态。

我机固定训练完成,将经过大量回合训练好的模型保存,改变地图参数,让我机具有速度并扩大地图尺寸,目标速度降低为与我机速度一致,验证跟踪模型的有效性。在MaCA环境中,对目标速度的改变并不会影响整体的代码结构,仅需在map地图中设置speed参数即可。使用图14展示了总验证回合为10、目标移动时的验证回报曲线。

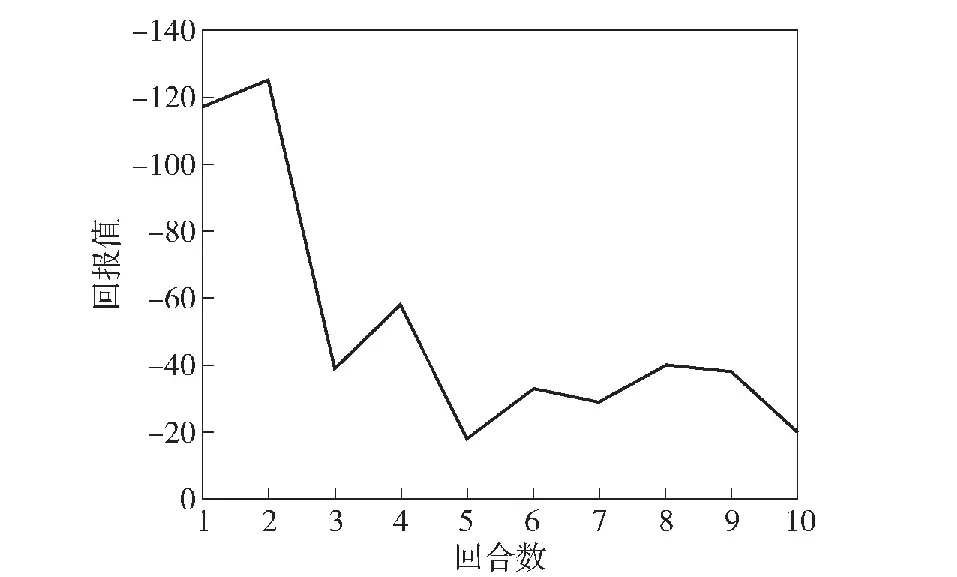
图14 我机移动时跟踪验证的回报曲线Fig.14 Reward curve for tracking verification when our UAV is moving

由图14可见,当我机运动时回报值依旧较小,通过10回合的验证(非训练),如图15所示,发现我机能在目标转向时完美同步追踪,跟踪效果显著,验证了训练模型的有效性。

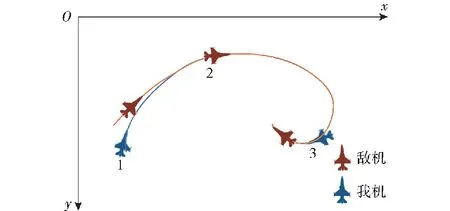
图15 验证演示过程示意图Fig.15 Schematic diagram of verification demonstration

3.3.2 对照实验

采用DDPG算法作为对照,环境设置相同,通过调整超参数得到我机运动的情况下最优跟踪训练的回报曲线如图16所示。

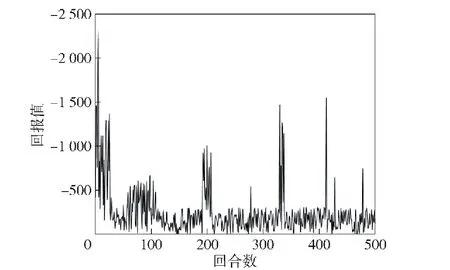
图16 基于DDPG的跟踪训练原始回报曲线Fig.16 Original reward curve of tracking training based on DDPG

DDPG算法处理该问题同样具有收敛趋势,但相较于SAC算法曲线波动大,回报值没有稳定在0附近。这是由于DDPG算法对超参数极其敏感,略微调整学习率就可能导致训练结果不收敛。此外,DDPG算法只选择一个最优策略,而不考虑等优策略,这影响了算法稳定性及迁移性。而SAC算法同时最大化策略熵与回报期望,能够学到等优策略,此外,SAC算法对于不同的随机数种子等超参数能够达到同样的收敛效果,稳定性能也更加出色。

3.4 干扰规避元策略训练

我机相对于目标的方位角为α1,目标的航向角为α2,我机的航向角为α3,目标航向角与方位角度差值为Δ1,方位角与我机的航向角差值为Δ2,两机间距记为d。可以根据目标航向角与方位角差值以及中值π来构造观测值和奖励函数。同样地,先对观测值进行预处理,取cos(|Δ1-π|)作为观测值,由于|Δ1-π|≤π,当Δ1距离中值π越近时,观测值越大且附近越平缓,表明状态很好。相反当距离中值越远时,观测值越小,且附近的观测值变化不大,表明状态很差。

奖励函数的构建需要记录当前状态下的目标航向α2,目标坐标(x2,y2),下一状态下的方位角α1s,我机坐标(x1s,y1s)。计算两个状态下的坐标距离衡量采取的动作是否减小了距离,记作

d=(x1s-x2)2+(y1s-y2)2

(11)

奖励函数第1部分构造为

R=-(α2s-α1)2·d

(12)

奖励值越大,表明我机航向角与目标方位角之间夹角越小,我机与目标之间的距离越近。

奖励函数第2部分构造为区域奖励,判断当前状态目标的航向角与下一状态方位角之间的差距是否在[175°,185°]和[-175°,-185°]内,如果在该范围内,则奖励函数为

R=-1 000·|cos(10(α2-α1s))|

(13)

该奖励值越小,表明距离干扰中线越近,并且在远离干扰中线的方向奖励值梯度很大,引导我机优先进行干扰区的规避。最终观测值构造为cos(|Δ1-π|)、Δ2、α2、α1、d。超参数设定同3.3节。

通过图17的回报曲线可见随着训练的进行,整体训练过程达到收敛状态。观察整个追踪加躲避干扰的演示过程,如图18所示,可以明显看到我机在初始位置受到目标干扰时,选择快速逃离干扰区,逃离成功后对目标进行追击。

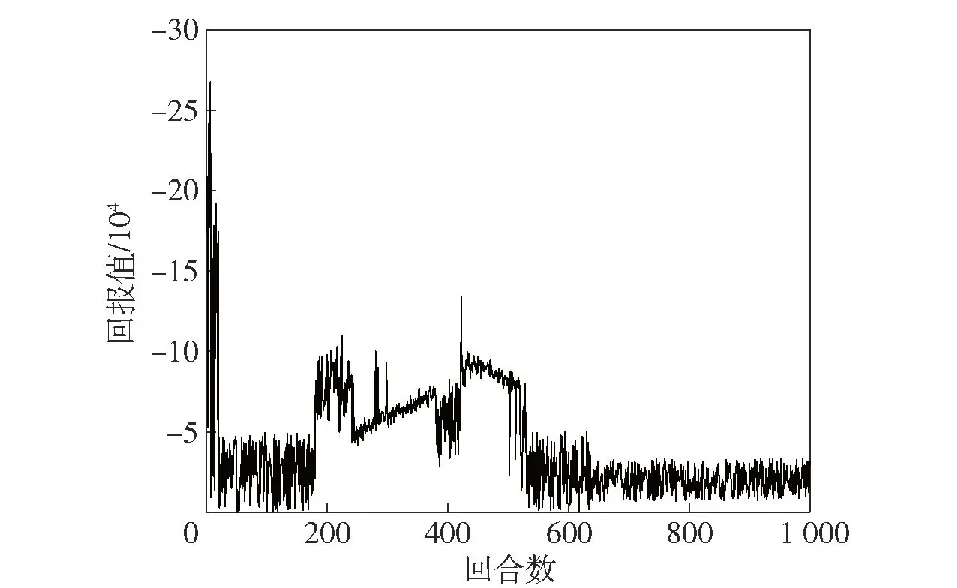
图17 跟踪加规避干扰的回报曲线Fig.17 Tracking plus distraction avoidance payoff curve

图18 干扰规避与追踪演示图Fig.18 Interference avoidance and tracking demo

3.5 分层框架构建

3.5.1 回报奖励设计

模型训练需要的回报奖励依据不同的元策略分别设置。7种元策略的具体奖励设置方案如下：

1)针对目标探测策略,设置固定时间步长τ1,发现目标则应该由β(s)控制结束该选项。发现目标给予奖励Ro=10。

2)针对武器选择与目标打击策略,成功打击一次目标记奖励为Rh=100,若打击列表仍存在打击目标,则应给予与终止函数概率呈反比的惩罚项：

(14)

3)针对队形转换策略,在对局开始阶段与我机战损时完成策略执行记一次集群奖励Rg=30。

4)针对雷达开关策略,成功完成开关切换动作记一次开关奖励Rs=20。

5)针对主动干扰策略,探测到目标频点并成功设定干扰频点记一次干扰奖励Rj=100。

6)对于目标追踪策略,发现目标时提供最大策略奖励,记作Rc=100。

7)对于干扰规避策略,我机位于目标干扰区域时提供给最大策略奖励,记为Rm=100。

3.5.2 决策模型构建

选项模型构建结构与一般Option-Critic结构不同,在训练时采取之前已经构建好的元策略模型,通过封装好的元策略模型,输入环境状态返还动作,即放弃Option-Critic自动训练策略,这是因为采取Option-Critic方法训练的元策略无法将动作序列具体化为符合人类逻辑与经验的策略,且容易过拟合到某个动作,而非序列动作。改进后的方法只通过Actor-Critic网络训练得到终止函数,给出元策略在不同状态下完成执行的时间。Critic网络根据状态及奖励更新选项价值函数Q值以及选项间的优势函数,梯度反向传递Actor网络完成参数更新给出终止函数。决策模型算法流程与示意图如图19与图20所示。

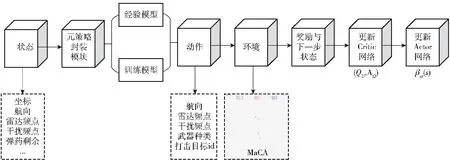
图19 决策模型算法流程Fig.19 Process of decision-making model algorithm

图20 多维决策算法执行示意图Fig.20 Schematic diagram of multi-dimensional decision-making algorithm execution

3.6 仿真实验结果分析

3.6.1 1v1对战结果

由于MaCA环境截图效果无法显示作战流程,这里通过记录实际数据绘制具有说明意义的局部作战轨迹,给出作战示意图。

图21展示了我机探测到目标之后选择目标追踪策略对目标展开追踪,能够精准锁定目标方位并进行追踪;在追踪过程中干扰开机且干扰频点发生转变,说明采取了主动干扰策略;与此同时,开启干扰规避策略规避目标干扰,从示意图中可见我机绕开了目标的干扰区域成功规避目标干扰。

图21 分层强化1v1的仿真验证示意图Fig.21 Schematic diagram of simulation verification of hierarchical reinforcement 1v1

与多机不同的是,在1v1中,由于没有友机提供目标的位置坐标信息,我机判断是否进入干扰区的条件是目标上一时刻所处探测区域的角度以及目标是否丢失,如果处于探测区域的边缘且目标丢失,则需要重新搜索,被干扰概率很低。如果处于探测区域中央且下一时刻目标丢失,则大概率由于目标干扰造成,从而判断出我机位于目标区,此时将假定目标在上一时刻的方位且朝向我机,我机需要躲避该固定干扰区域;将目标引导到攻击区,在适当的距离选择攻击动作并成功打击目标。

各个策略的执行动作均以合适的时机完成切换,且策略执行的终止函数能够正确地在不同状态终止正在执行的策略。通过20轮的算法演示验证,我机(红方)均取得胜利,以100%全胜的战绩战胜了目标算法,验证了该分层强化决策的有效性。

3.6.2 4v4对战结果

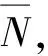
表1展示了10回合中雷达开关与否的被动发现次数统计,可见采用雷达开关策略能够大幅减少目标被动发现我机的频次,减少因目标被动探测暴露我机位置的概率。这点对于在执行异构的情况下我机执行的掩护任务尤为重要。

表1 10回合雷达开关与否的被动发现次数统计Table 1 Data of the number of passive discoveries with or without radar switch in 10 rounds

图22展示了10回合中雷达开关与否被动发现次数的平均统计柱形图,可以直观看出采用雷达开关策略目标被动探测到我机平均次数为13次,而禁用雷达开关策略被动探测次数上升到平均20次,证明了在分层决策下雷达开关策略的有效性。

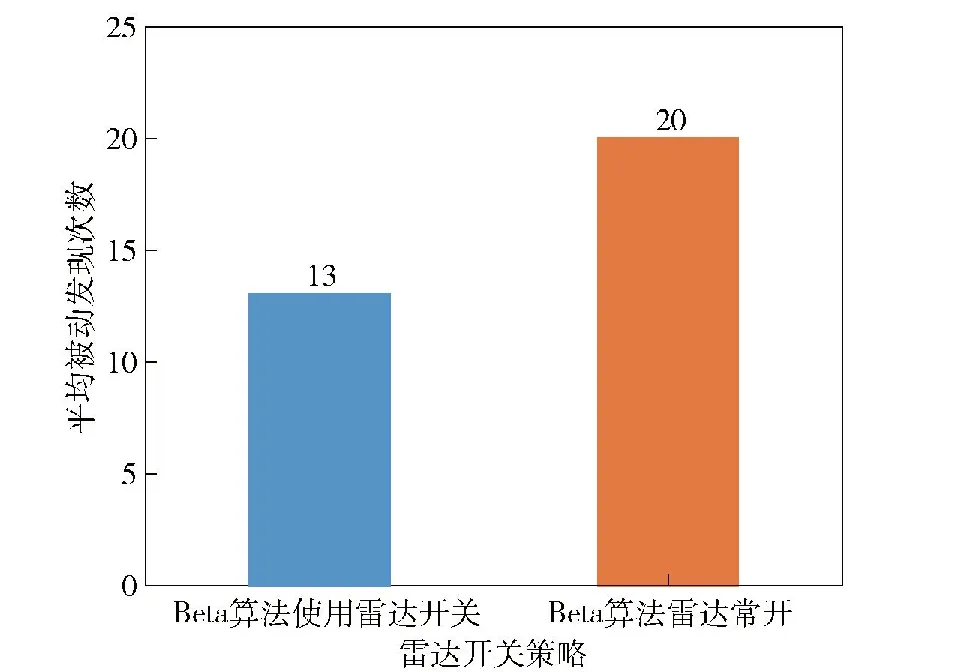
图22 使用雷达开关策略与否的平均被动发现次数对比Fig.22 Comparison of average passive discoveries with and without radar switch strategy

图23所示为Beta智能体可以在回合开始完成初始化编队,以长机-僚机编队进行目标的探测与干扰,这种初始编队能够优先取得信息优势,实现压制干扰,在我方无损毁的情况下歼灭两架目标,在开始便掌握数量优势。我机编队在歼灭了受压制干扰的目标之后终止函数停止编队决策,策略选择器根据当前状态选择其他元策略。队形转换策略在作战过程中能够在我机队形被破坏的情况下完成编队重组,重组后以编队形式对目标进行压制干扰,避免了因单独作战敌我同时发射导弹而互换的情况。

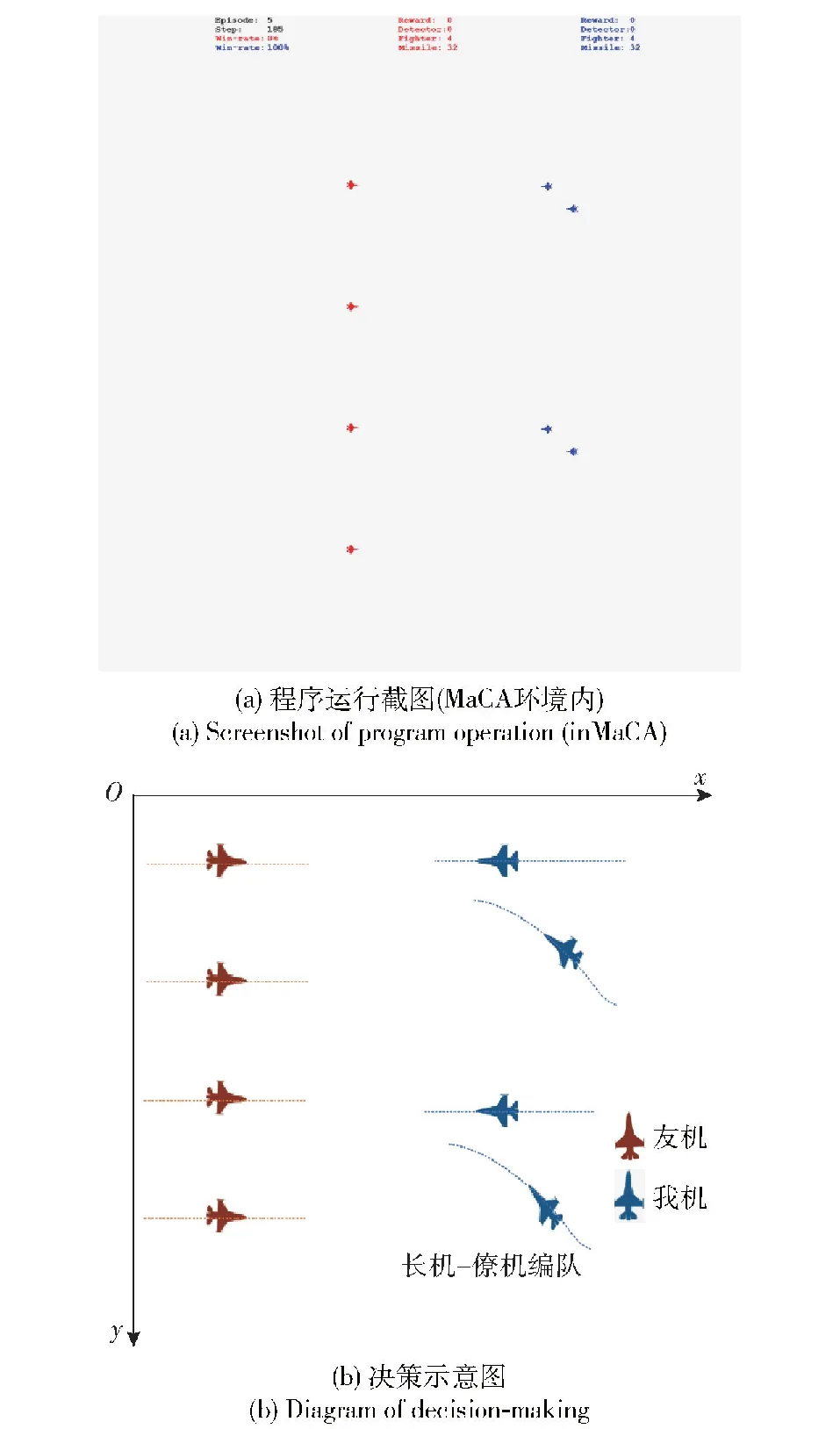
图23 初始编队Fig.23 Initial formation

为验证队形转换策略的有效性,统计了10回合内编队重组后该编队50步内的打击情况以及损失情况。记编队成功打击目标数量为S,编队成员损失数量为D,每局的数量统计如表2所示,其中,S与D均为0时代表本局编队结构未损坏。编队重组后协同打击仿真如图24所示。

表2 10回合队形转换50步内打击与损失统计Table 2 Data of strike and loss within 50 steps in 10 rounds of formation change

图24 编队重组后协同编队打击目标Fig.24 Cooperative formation striking the target after formation reorganization

从表2中的数据分析可知,除第2、5、6、8回合我机编队结构没有破坏外,其他回合重组的编队均完成了目标的压制打击任务,且仅有第7回合在编队执行搜索任务过程中损失1架战机,其他回合均无战机损失,验证了分层决策下队形转换策略的有效性。

图25展示了Beta算法能够在友机阵亡时指导我机向阵亡方位进行搜索,由于友机阵亡时代表目标在附近活动,前往该区域附近进行搜索能够大幅增加截获概率,充分展现了决策的智能性。

图25 友机阵亡我机搜索决策Fig.25 Our UAV’s search decision when friendly UAVs are killed

目标探测策略中的分布式搜索采用了人工势场中的斥力场,能够维持友机间距,避免探索重复区域。图26展示了我机分布式搜索策略,当友机相互靠近时会采取相互远离的动作。分层决策下,Beta成功在我机雷达未发现目标时选择目标探测策略完成分布式搜索,验证了目标探测模型的有效性。

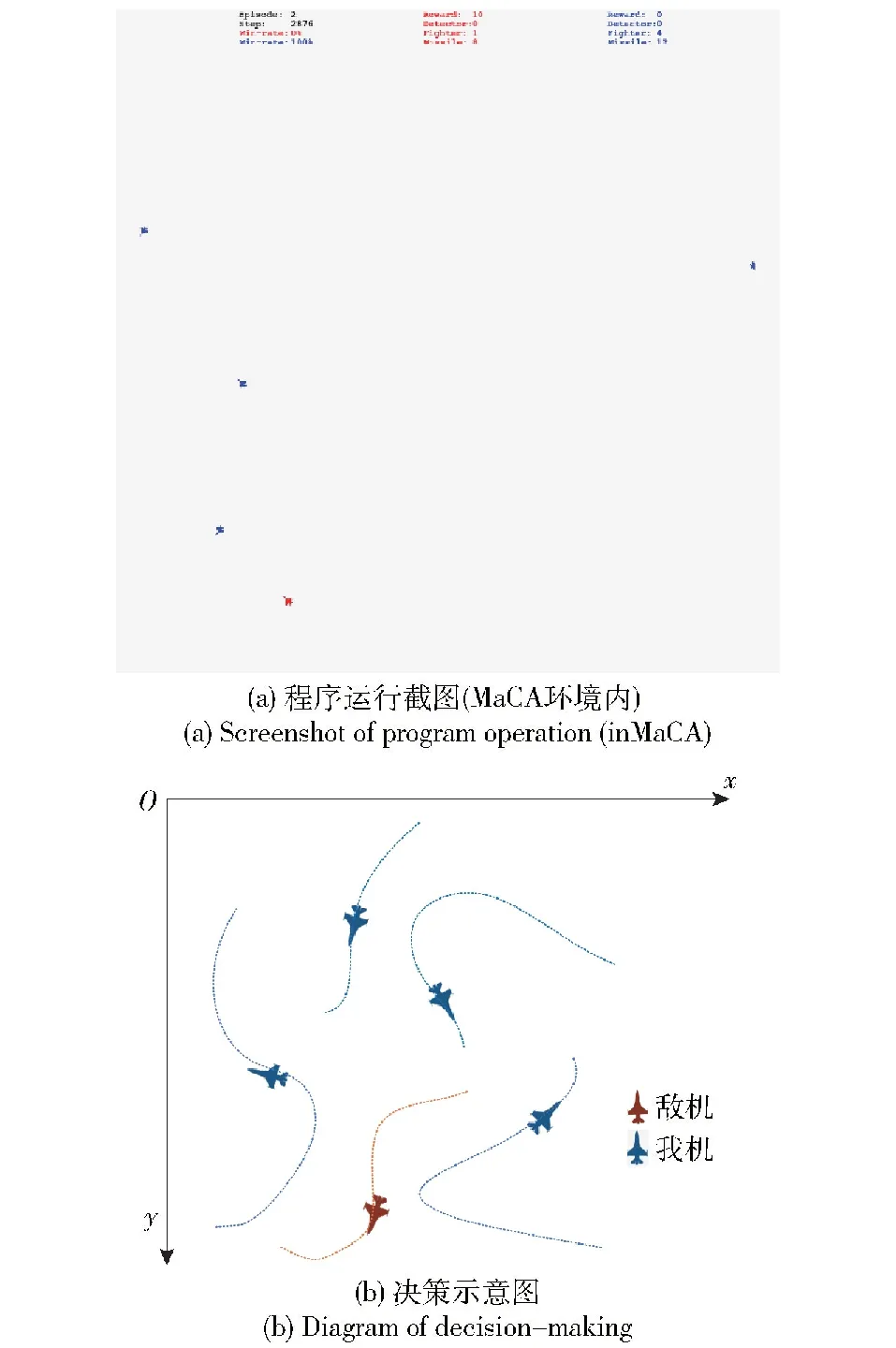
图26 分布式搜索Fig.26 Distributed search

图27蓝色实线表示导弹发射并命中,展示了我机武器选择和打击决策。为验证分层决策结构是否可以准确完成先敌打击,需要考量我机采取武器选择与目标打击策略时我机与目标的距离是否恰为导弹攻击区的边缘。为此,统计了10轮全流程作战过程中选择打击时我机与目标平均距离,记为D1,给出该距离与攻击区边缘距离的差距,记为Δ1,相关数据记录如表3所示。

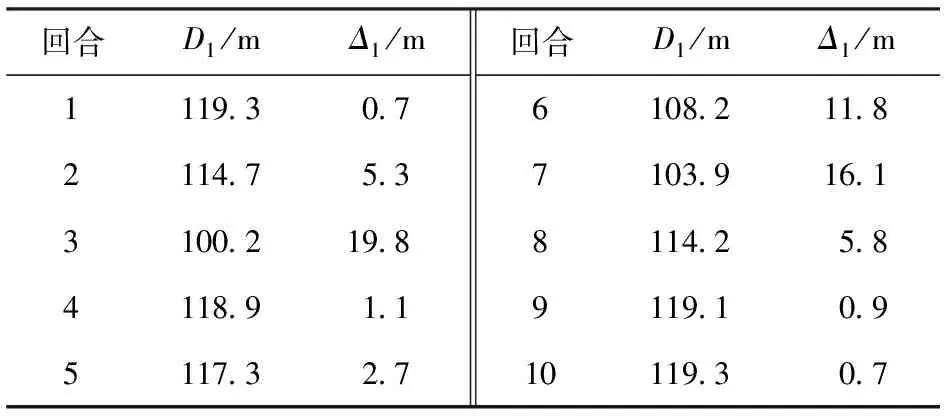
表3 10回合队形转换50步内打击与损失统计Table 3 The gap between the current distance and the edge of the attack zone in 10 rounds

图27 打击演示Fig.27 Strike demo

从表3中的数据可见,平均每局Beta采取打击决策时距离误差不超过20 m,充分展现了分层决策在武器选择与目标打击的及时性与有效性,同时说明了终止函数训练的有效性。

此外,该图还展示了我机编队对目标进行压制干扰,让目标探测系统瘫痪从而无法对我机做出打击动作,虽然目标的探测能力与武器与我机完全一致,但由于受到干扰无法第一时间向我方发射导弹,从而可以使我机编队完成优先打击,主动干扰策略的有效性也体现于此。

对于武器的使用情况,为避免我机对同一目标发射多发导弹从而导致武器弹药的浪费,采取了打击目标分配方法。为验证该方法的有效性,统计了每局作战结束导弹的使用情况。结果表明,每局导弹消耗量均为4,即一发导弹打击一个目标,利用效率为100%。

为分析全流程作战分层决策Beta模型的有效性,本文定义了平均战损,描述为平均每局对决的无人机损失数量,由表4与图28可见在10场对局中Beta算法平均每局损失1.4架战机,黑盒算法fix_rule_no_att平均损失3.8架,充分说明了结果表明Beta算法以全胜的战绩击败了黑盒算法。

表4 作战结果Table 4 Combat result

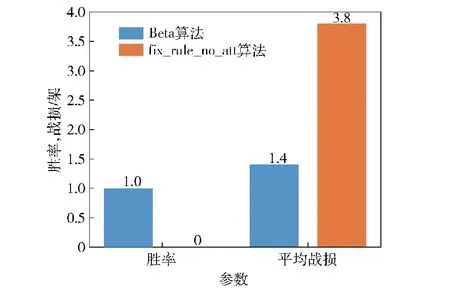
图28 算法对比Fig.28 Algorithm comparison

4 结论

本文对无人机多维空战自主决策展开研究,分析了现有研究成果以及不足。针对相关研究缺乏多维决策的问题,提出了采用分层强化学习完成无人机多维决策模型构建以及训练方法的构建。本文提出的多维空战自主决策分层算法通过改变传统Option-Critic框架,结合传统选项框架能够引入专家经验的优势,同时无需设计终止函数,通过训练完成元策略的灵活切换,算法扩展性强、层次分明、策略意义显著。在MaCA环境完成红蓝对抗仿真,对空战战术决策以及自主空战的多元化发展具有重要意义。得到主要结论如下：

1)元策略训练收敛,仿真验证能够很好地完成目标跟踪、干扰规避等任务。

2)该算法能够在不同状态下完成最优策略切换,并以全胜的战绩击败黑盒算法fix_rule_no_att。

下一步工作重点为：将训练环境迁移到三维,提升状态动作空间的复杂度,引入动力学模型,引入侦察机将同构问题转化为异构问题,将该算法应用到更贴近真实空战的环境中进行测试。此外,该算法部分元策略基于专家经验,后续将完全去经验化,建立全训练模型。