航空集群一发多收有源定位最优构型
2023-07-10王维佳王玉冰田瑾毛昭军杜琳琳
王维佳,王玉冰,田瑾,毛昭军,杜琳琳
(1.军事科学院 系统工程研究院,北京 100020;2.93236部队,北京 100085;3.武警工程大学,陕西 西安 710086)
0 引言
面对现代战场环境的高动态、深度不确定性特点,依托航空集群平台执行定位跟踪任务能够获得更广的观测范围、更高的定位精度以及鲁棒性,从而大幅提升战场态势感知能力[1]。因此,国内外学者均对集群定位做了大量研究,杜晶等[2]研究了基于时差频差的无人机集群协同定位模型;Dogancay等[3]基于Fisher信息矩阵(FIM)推导了基于到达角(AOA)定位、到达时间差(TDOA)定位对应的最优构型并应用在无人机集群无源定位中;杨俊岭等[4]在分析了无人机集群AOA定位后,引入演化深度神经网络进行无人机集群动态航迹规划;钟日进等[5]提出集群内测距和对目标测向的协同定位方法,即集群内进行测距提升平台之间相对测量精度,同时给出基于AOA协同定位求解算法。当前的研究多基于TDOA、AOA、到达信号强度等定位体制进行无源定位,其前提是目标辐射源向外辐射电磁信号,一旦目标进入电磁静默模式,集群平台无法获取目标信息,因而无法进行无源定位跟踪任务。
本文在借鉴双多基地组网雷达[6-7]以及外辐射源无源相干定位[8-9]技术的基础上,提出基于到达时间(TOA)椭圆定位的航空集群一发多收协同定位方法,在无源定位的基础上增加集群内的己方合作有源发射机,从而实现对电磁静默目标的定位跟踪。
航空集群一发多收有源协同定位跟踪方式如图1所示,集群内平台按角色分为发射机和接收机:发射机通常位于战场的后方,处于较安全范围,起到主动发射、数据处理与指挥控制中心的作用;多个接收机平台处于战场前方,与发射机保持一定距离,主要负责接收从目标反射的回波信息,接收机不主动发射电磁波,隐蔽性好,从而保证平台的安全性。航空集群有源协同探测在性能上优势互补、分工协作,充分发挥各自能力,进一步扩大空中的纵深探测范围,延伸作战半径。图1中xTr为发射机位置,xTr=[xTr,yTr]T,xi为接收机位置,xi=[xi,yi]T,i=1,2,…,M,M为接收机数量,xt为目标位置,xt=[xt,yt]。
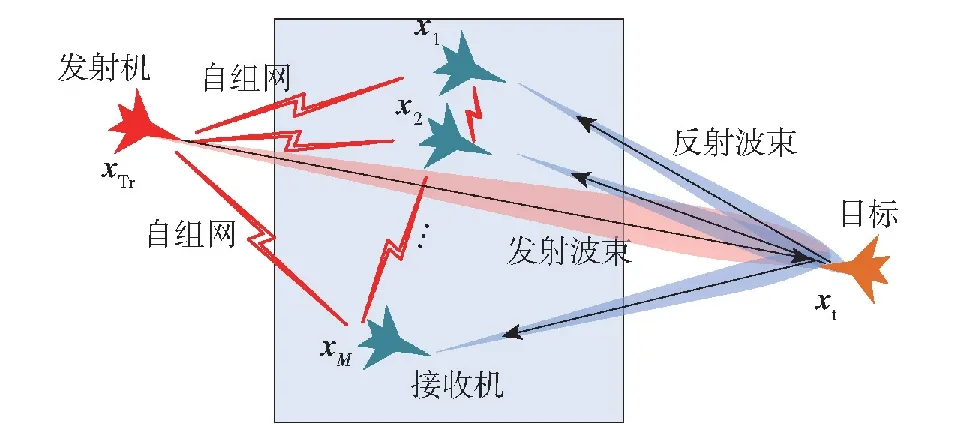
图1 航空集群一发多收有源协同定位跟踪示意图Fig.1 Active localization with one transmitter and multiple receivers in aircraft swarm
因此,采用一发多收的协同定位跟踪可以有效应对目标辐射源关机的情况,同时具备反隐身能力。对于一发多收的航空集群定位系统,各接收站为副站,主要完成对合作信号的侦收、时间信息提取;发射机为主站,需要对各个副站的测量值进行融合处理,解算目标状态信息,同时依据当前态势对集群的构型进行优化,并将决策控制指令分发给各个接收机。
与传统定位方式不同,集群定位性能除了受到定位体制、定位算法的影响外,还受到集群规模、集群构型的较大影响,因此本文从定位构型优化准则出发,主要分为两个方面开展研究:一是在有源TOA定位体制下,推导不同接收机数目对目标进行定位的最优几何构型,即得到最优构型的解析解;二是怎样将得到的最优构型运用到实际的航迹规划中,从而进一步提升定位跟踪精度。
1 一发多收TOA定位模型
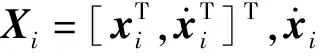

图2 一发多收定位跟踪示意图Fig.2 Active localization with one transmitter and multiple receivers
i(xt)=τi(xt)+ei
(1)
(2)
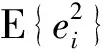
i=‖xt-xTr‖+‖xt-xi‖+ni
(3)

=[r1,…,rM]T+[n1,…,nM]T
(4)
假设n=[n1,…,nM],对应的误差协方差矩阵为
(5)
2 一发多收TOA定位最优构型分析
克拉美-罗界(CRLB)表征了估计参数的无偏估计方差的下限,体现出估计问题本身的属性,与具体的定位或跟踪算法无关,可以作为定位性能的好坏准则。因此,基于CRLB可以对TOA定位的最优构型进行分析,在具体分析过程中,由于CRLB为矩阵形式,通常采取两种准则[12]:
1) D优化准则,最大化Fisher矩阵J的行列式:arg max det (J);
2) A优化准则,最小化CRLB矩阵的迹:arg min det (J-1);
本节拟分别采用两种准则对TOA定位的最优构型进行分析。
2.1 基于D优化准则的一发多收最优构型分析
根据通用矩阵FIM矩阵求解方法,可以得到TOA椭圆定位的FIM矩阵[13]为
(6)
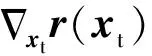
(7)
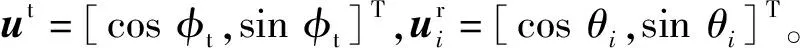
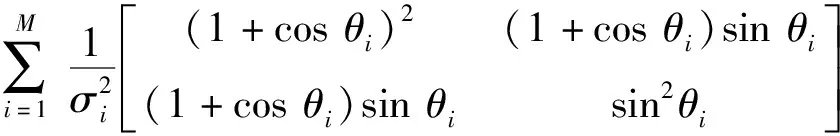
(8)
由D优化准则对该构型进行分析,此时的优化目标函数取值与方位角θ=[θ1,…,θM]有关,可以表示为
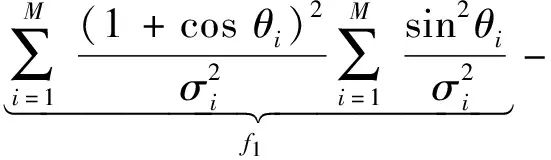
(9)
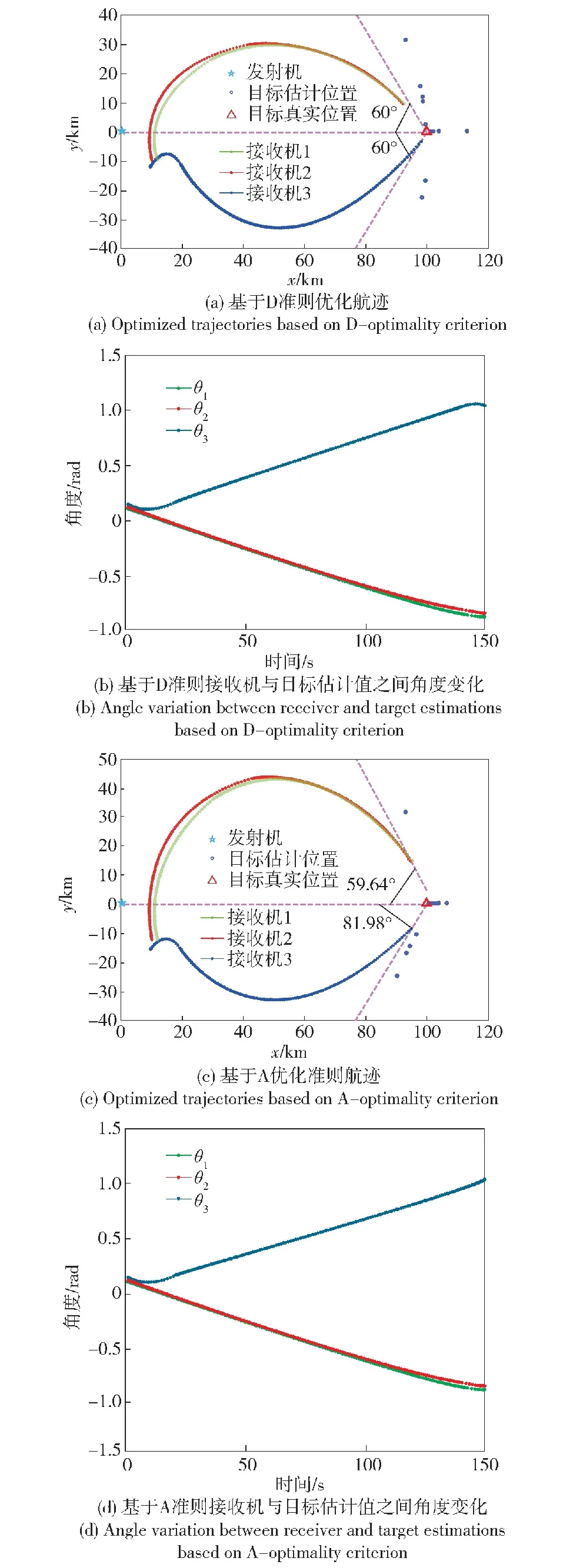
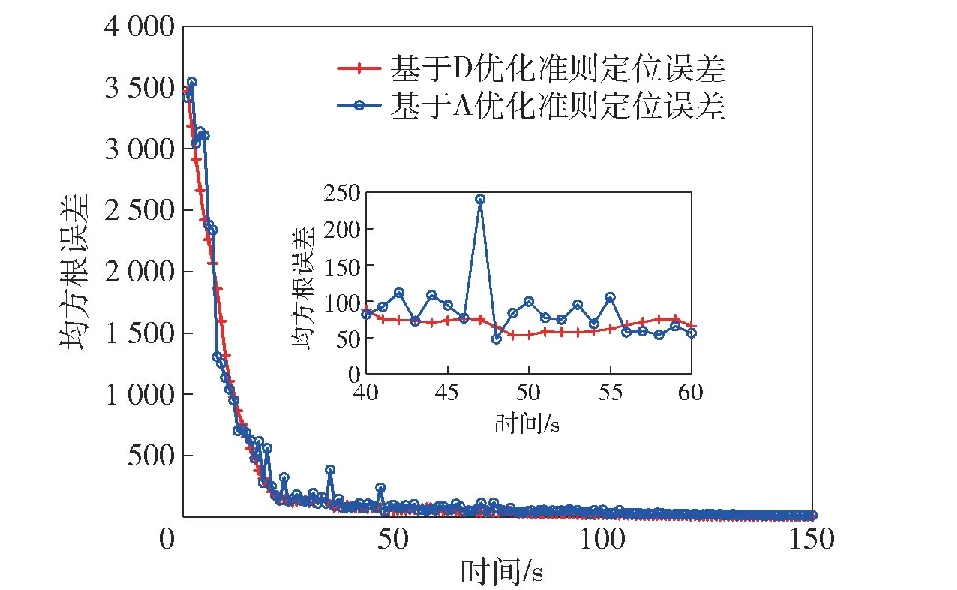
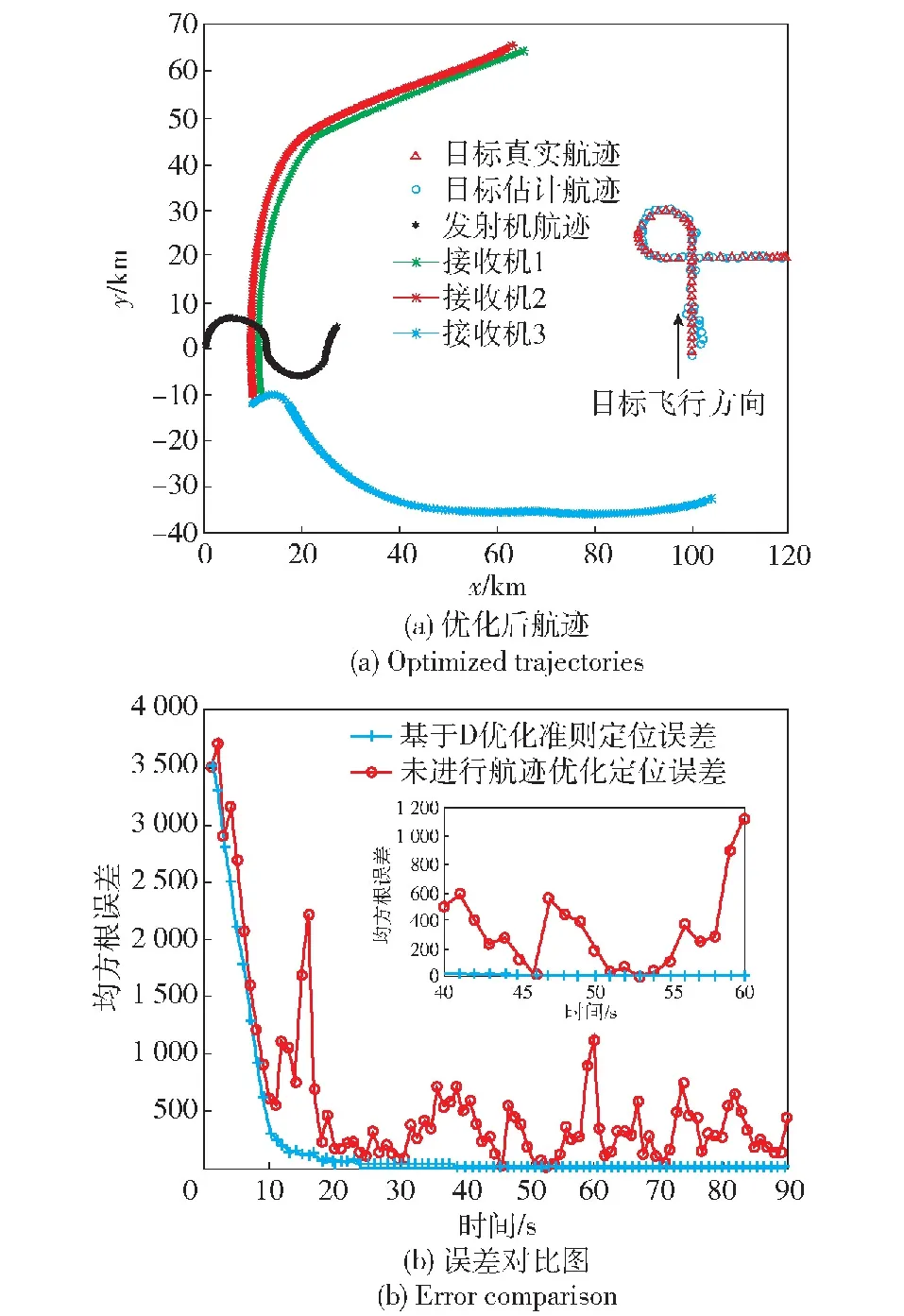
假设ai=(1+cosθi),可知ai的取值范围为0 (10) 式中:a=[a1,…,aM]。由幂均值不等式可得 (11) 仅且仅当a1=a2=…=aM时,式(11)的等式成立。对于ai>0,由基本不等式可得 (12) 将式(12)代入式(10),可得 (13) (14) a1=a2=…=aM=3/2,则各个接收机之间的最优角度为 |θi|=π/3 rad (15) 由于目标函数的第2项为f2≥0,因此整个目标函数f(θ)的最大值在f1(a)=f1,max(a)、f2=0处取得,可得: 1) 当M为偶数时,对应的最优定位构型为 (16) (17) 2) 当M为奇数时,无法同时满足式(16)中 2个条件,因而无法直接得到整个目标函数的最大值。此时,式(10)可以变形为 (18) 对式(18)求θi的偏导数,并使其等于0,可得 (19) 从而可得,取极值的条件为或者{θi,θj}={π/3 rad,-π/3 rad}。当时,显然f(θ)=0,此时发射机、接收机以及目标成一条直线,对应着最差的定位构型。而当{θi,θj}={π/3 rad,-π/3 rad}时,对于奇数个接收机,目标函数的最大值为 (20) (21) 图3 基于D优化准则的最优构型示意图Fig.3 Optimal configuration based on D-optimality criterion 2.1节采用D优化准则对一发多收情况下TOA椭圆定位的构型进行了分析,证明了无论接收机数目为奇数还是偶数,对应的最优构型都和发射机与目标之间连线的夹角为π/3 rad。 本节采用A优化准则进行分析,此时的优化目标函数变为 (22) 假设λ1、λ2分别为式(8)的两个特征值,其中λ1≥λ2,从而可得CRLB的特征值为 (23) (24) 同样,假设ai=(1+cosθi),此时式(22)可以化简为 (25) 对于不等式: (26) 等号成立的条件为 a1=a2=…=aM=a (27) 因此可得: (28) 进一步对式(28)化简可得,当a=4/3时,不等式右边取得最大值: (29) 为了满足式(24),对于偶数个接收机,最优的构型可以表示为 (30) 图4给出了一发四收情况下,采用TOA椭圆定位的最优构型示意图,偶数个接收机被分为两组,与目标连线之间的夹角为θi=±arccos(1/3)·180/π=±70.35°。 图4 基于A优化准则的一发四收最优构型示意图Fig.4 Optimal configuration with one transmitter and four receivers based on A-optimality criterion (31) |θi-θj|=2θ0 (32) 式中:θ0=arccos(1/3)。因此奇数个接收机对应的最优角度为 (33) 图5 M=3时的变化范围Fig.5 Variation of when M=3 图6 基于A优化准则的奇数个接收机最优构型Fig.6 Optimal configuration with odd number of receivers A-optimality criterion (34) A准则下3个接收机最优构型对应的FIM矩阵为 (35) 同理,4个接收机最优构型对应的FIM矩阵为 (36) (37) 通常情况下,采用D优化准则与采用A优化准则得到的最优构型相同,而通过本节分析,在TOA椭圆定位中,基于A优化准则得到的最优构型与D优化准则的最优构型不同,其最优构型与接收机数目的奇偶性有关。两种优化准则均可以作为优化目标函数作为定位性能好坏的标准。 第2节给出了不考虑接收机平台约束情况,TOA定位跟踪最优构型的解析解。但在实际应用中,集群接收平台受到自身运动约束的影响,无法在短时间内达到对目标定位最优构型的条件[16]。尤其是在没有目标先验信息的情况下,目标与航空集群之间的距离可能较远,受到平台速度、转弯角速度等影响,需要经过一定时间才能够达到最优的定位跟踪构型,才能够得到更好的定位效果。因此如何将理论推导的最优构型应用到集群航迹优化中,提升对目标的定位跟踪效果是本节需要解决的问题。 假定航空集群接收机系统的离散动态模型[17]为 Xk+1=f(Xk,uk) (38) 式中:Xk为k时刻系统的状态值,Xk=[x1(k),x2(k),…,xi(k),…,xM(k)]T,xi(k)为k时刻接收机i的位置;uk为每个时刻集群接收机平台飞行方位角的控制量,uk=[u1(k),u2(k),…,ui(k),…,uM(k)],ui(k)为k时刻接收机i的飞行方位角控制量。由此可得离散情况下航空集群的运动方程可以简化为 (39) 式中:v0为平台飞行速度;T为接收机采样时间间隔。如图7所示,在每一采样时间内,应用定位算法更新目标位置,计算目标位置更新后接收机相对发射机与目标连线的角度θ=[θ1,θ2,…,θM]T,同时分别以A、D优化准则为优化目标函数,得到下一时刻各个接收机的控制量uk+1,因此目标函数与平台约束可以表示为[18] 图7 航空集群寻找最优航迹示意图Fig.7 Schematic diagram of finding optimal trajectory for aircraft swarm (40) s.t.‖ui(k+1)-ui(k)‖≤umax (41) ‖xi(k+1)-xt(k)‖≤Rh (42) ‖xi(k+1)-xt(k)‖≥Rl (43) ‖xi(k+1)-xj(k+1)‖≤ch (44) ‖xi(k+1)-xj(k+1)‖≥cl (45) 式中:约束条件式(41)表示平台自身方位角约束,它限制了生成的航向最大偏角umax,该约束取决于集群平台的机动性能;条件式(42)、式(43)分别表示集群平台到目标之间的距离约束,距离上限Rh主要由接收机接收信号的信噪比决定,距离下限Rl为集群平台与目标之间的安全距离;条件式(44)、式(45)分别为平台之间通信约束以及集群内平台防相撞约束,ch、cl分别为平台之间距离的上限和下限。 由上面航迹优化问题可以转变为带约束的非线性优化问题,本文直接借鉴自适应惩罚函数的方法[19]进行求解。 综上可得,基于A、D优化准则(实际应用过程中A、D优化准则选择其中一个)的航空集群有源定位航迹优化方法的数据处理流程如图8所示,其步骤如下: 图8 基于A/D优化准则的航空集群航迹优化处理流程Fig.8 Trajectory optimization process of aircraft swarm based on A/D-optimality criteria 步骤1给定时刻航空集群接收机系统状态Xk=[x1(k),…,xM(k)]T,发射机发射波束,各接收机接收目标反射波束,得到接收机的TOA量测值,以及约束条件式(41)~式(45)。 步骤2利用3次最小二乘TOA定位算法[20]求解出当前时刻对目标的估计值t(k)。 步骤3以该时刻目标估计值当做该时刻目标真实值,在约束条件式(41)~式(45)情况下,利用智能优化算法产生各个接收机下一时刻可行的控制量,分别计算在不同控制量uk+1下,接收机相对发射机与目标连线的角度θ=[θ1,θ2,…,θM]T,分别计算以A、D优化准则为优化目标函数式(40)。 步骤4利用自适应罚函数法将该非线性约束转化为极小化辅助函数的无约束问题,先通过寻优找出遗传算法中具有较好质量的不可行解,然后再引导种群向可行域或者最优解逼近,记录该最优解对应的接收机控制量。 航空集群中接收机的初始运动状态为x1(1)=[-9 200 m,-5 000 m]T、x2(1)=[-10 000 m,-5 000 m]T、x3(1)=[-10 000 m,-5 800 m]T、x4(1)=[-9 200 m,-5 800 m]T。初始时刻各个接收机的机头指向均为π/2(朝向y轴),固定飞行速度为v0=200 m/s采样时间间隔T=1 s,仿真时间为150 s。集群平台的航向角约束为umax=15°,最大和最小探测距离分别为Rmax=20 km、Rmin=0.3 km。 图9给出了基于D优化准则与A优化准则的航迹对比。由图9(a)与图9(b)可知:当发射机与目标静止,3个接收机自动分为两个子群朝向目标飞行,同时两个子群与目标之间的夹角不断扩大并分别位于发射机与目标连线的两侧;大约经过140 s,两个子群与该连线之间的夹角均为60°,与理论分析相吻合。图9(c)与图9(d)给出了基于A优化准则的飞行航迹。与D准则形成的优化航迹的形状大致相同,不同之处在于,最终与目标形成的最优构型角度不同。 图9 基于D优化准则与A优化准则的航迹对比Fig.9 Trajectory comparison based on A and D-optimality criteria 图10给出了基于D优化准则与A优化准则的误差对比,整体上A准则对应的平均误差值相对较小,但对应的计算量较大对应的求解需要的时间较长,同时在某些时刻求解CRLB值的过程中有奇异值的出现,导致算法的稳定性弱于D优化准则。因此在实际应用中,可以优先采用D优化准则,能够在提升精度的同时确保算法的稳定性与实时性。 图10 基于D优化准则与A优化准则的误差对比Fig.10 Error comparison based on A and D-optimality criteria 4.1节对TOA椭圆定位的最优构型进行验证,因此本节主要针对实际运用过程中发射机、目标均运动情况下,进行验证。 假设集群平台之间的通信距离约束为ch=15 km,防相撞约束为cl=0.2 km。采用D优化准则得到的优化后定位结果如图11所示。 图11 航空集群有源定位优化Fig.11 Active localization optimization of aircraft swarm 由图11(a)可得,3个接收机依然按照图10类似的航迹飞行,同时由于发射机、目标的位置处于动态变化中,接收机每个时刻均按照新的位置进行构型优化,最终得到优化后飞行航迹。 在实时性方面,基于A/D优化准则的航空集群航迹优化方法中最大的计算量来源于优化算法对各个接收机最优控制量的计算。为了保证优化算法能够高动态的航迹规划任务。实际仿真中,一是充分考虑集群平台的航向角约束umax=15°,从而将每个步长中的寻优范围约束到[-15°,15°]之间,大大缩小了寻优空间;二是采用了自适应罚函数与遗传算法相结合,充分利用罚函数法的优点,进一步减小了算法计算量,保证了实时性。 为了对构型优化有效性进行验证,将经过构型优化后的定位结果与接收机随机产生航迹点的定位结果进行对比,结果如图11(b)所示。通过图11(b)对比可得,未经过构型优化的定位结果误差较大且具有较大的不稳定性,主要因为在某些时刻集群接收机平台与目标的相对构型非常不利于对目标的定位。采用D优化准则的优化航迹能够在尽可能短的时间内降低定位误差,且具备持续优化能力。 本文针对航空集群一发多收有源协同定位运用问题,研究了一发多收有源协同定位最优构型与航迹优化方法。得出以下主要结论: 1) 基于A优化准则与D优化准则推导了不同接收机数目对目标进行定位的最优几何构型,分析最优构型的解析解,进一步提升有源协同定位效果,为航空集群有源定位构型优化提供了理论支撑。 2) 将得到的最优构型运用到航空集群航迹优化中,提出基于A/D优化准则的航空集群有源定位航迹优化方法,并通过仿真验证了其有效性。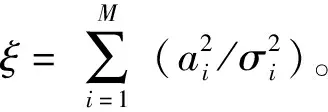
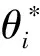
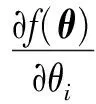


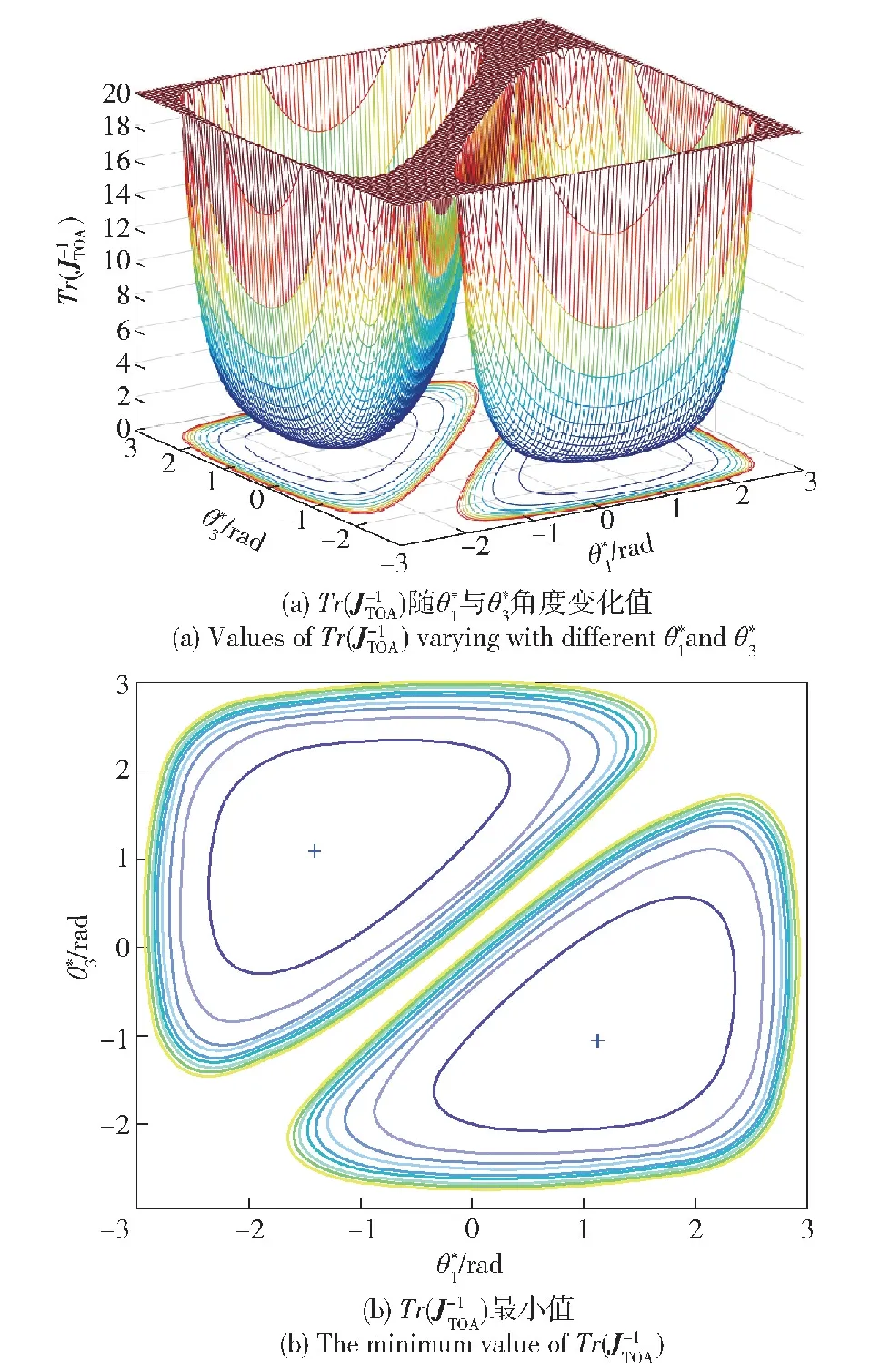
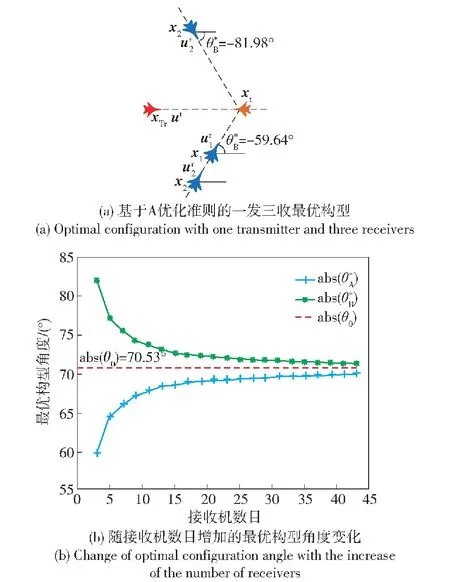
2.2 基于A优化准则的一发多收最优构型分析
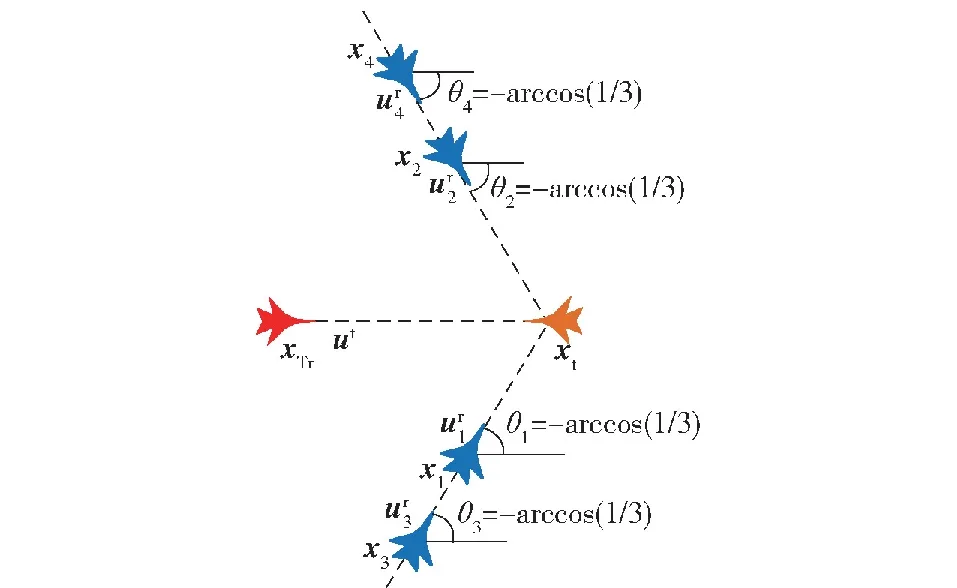
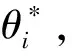
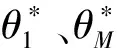

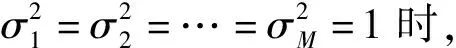
3 航空集群有源协同定位航迹优化


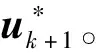
4 仿真验证
4.1 TOA椭圆定位最优构型验证
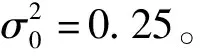
4.2 航迹优化
5 结论
