宽高比5∶1矩形断面涡激振动锁定区间内涡激力展向相关性分析
2023-07-10温青龙航华旭刚池俊豪孙洪鑫
温青 龙航 华旭刚 池俊豪 孙洪鑫

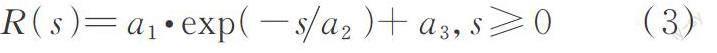
摘要 涡激力展向相关性是准确预测三维柔性结构涡激振动振幅的重要因素。以宽高比5∶1矩形断面为例,通过气动力展向相关函数理论建模和节段模型弹性悬挂测振、测压风洞试验,研究了涡激振动锁定区间内实测气动力展向相关性变化规律。研究结果表明:在涡激振动锁定区间内,实测气动力由完全相关的自激力和不完全相关的随机气动力组成,展向相关性可以用指数加常数型函数描述,指数项系数为随机气动力占实测气动力的能量比,指数项系数和常数之和等于1;实测气动升力均方根在涡振起振阶段最大,随着风速增大反而减小,随机气动力均方根基本保持不变,由此导致实测气动力展向相关性表现为起振阶段最强,随着风速增加而减弱。
关键词 涡激振动; 气动力; 展向相关性; 矩形断面
引 言
涡激振动是一种带有自激性质的限幅风致振动。目前,已有不少大跨桥梁主梁观测到在低风速下发生涡激振动事件,如虎门大桥[1]、鹦鹉洲大桥、西堠门大桥[2]等。涡激振动不会造成桥梁破坏,但是,长期的涡激振动会对桥梁的正常运营、行车安全性造成不利影响,缩短结构或者构件的使用寿命[1?7]。评价桥梁的涡振性能、预测涡振振幅是桥梁设计、运营管理普遍关注的问题。
大跨桥梁为典型的空间柔性结构,涡激力展向相关性是预测桥梁涡振振幅的重要参数。静止状态的圆柱、矩形柱、桥梁主梁等钝体断面刚性构件的气动力展向不完全相关,用指数函数能很好地描述气动力随展向间距的变化规律[8?10]。涡激振动状态的钝体断面实测气动力展向相关性增强,圆柱的涡激力展向相关性仍可用指数函数描述[8],而矩形断面、流线型箱型断面的气动力展向相关性呈现先减小后基本保持不变的特征[9?14],可采用指数加常数型函数描述[11]。在涡激振动锁定区间内,矩形断面和流线型箱型断面实测气动力展向相关性并非在涡振振幅最大处最强[9?14],而是展现出不同寻常的特征,值得探讨。
矩形断面是一种典型的钝体断面,其气动性能研究可为工程结构的气动性能评价提供参考。近年来,在国际风工程协会等组织倡议下,发起了宽高比5∶1矩形断面气动性能Benchmark研究[9?11,15?19],气动力展向相关性就是主要研究内容之一。这些研究均表明,在锁定区间内,起振阶段实测涡激力展向相关性最强,而在最大振幅时相关性反而弱。矩形断面涡激振动可以大致分为两类[20]:运动诱发涡激振动和卡门涡脱诱发涡激振动。Li等[19]通过强迫振动试验对宽高比5∶1矩形断面运动诱发气动升力和卡门涡脱诱发气动升力开展了精细研究,运动诱发气动升力展向相关系数约为小于1的常数,增大振幅,展向相关系数增大。宽高比5∶1矩形断面第二个锁定区间的涡激振动为运动诱发涡激振动,锁定区间内,实测气动力展向相关性随着风速和振幅增大反而减小,此现象有待进一步合理解释。
鉴于此,本文以宽高比5∶1矩形断面为例,通过气动力展向相关函数理论建模和节段模型弹性悬挂涡激振动风洞试验,研究了涡激振动锁定区间内实测气动力展向相关性变化规律,分析了实测气动力展向相关性随着振幅增大反而减小的原因。论文首先介绍了风洞试验概况,然后,详细给出了实测气动力及其展向相关特征,最后,通过展向相关函数理论建模分析了实测气动力展向相关规律。
1 风洞试验概况
风洞试验在湖南大学HD?2风洞的高速试验段进行,该试验段长17.0 m,宽3.0 m,高2.5 m,空风洞中来流风大于2 m/s时的湍流度小于0.5%。
节段模型宽度B为300 mm、高度D为60 mm,宽高比为B/D=5∶1,模型长度L为1540 mm。模型通过8根弹簧悬挂,如图1所示。悬挂系统的动力参数如表1所示,单位长度模型质量(me)为6.23 kg,频率(f)为7.04 Hz,阻尼比(ζ)为0.44%,Sc数(Sc=4πmeζ/(ρD2))为74.22。试验风速区间U为3.0~5.5 m/s。ρ为空氣密度。
沿模型展向变间距布置了13排测压孔,如图2(a)所示,每排测压截面布置32个测点,如图2(b)所示,共计416个测压点。风压采用电子压力扫描阀采集,采样频率为330 Hz,采样点数为10000。来流风速采用Cobra Probe测定,模型振动响应采用激光位移计测定,数据由DHDAS动态信号采集系统采集,采样频率为100 Hz。
节段模型的端部条件和长宽比综合影响节段模型的涡激振动特征以及模型上气动力的分布[21?22]。本试验长宽比为5.13,是大长宽比模型,涡激试验结果较为可靠,模型中间段存在均匀分布的气动力[21?22]。在进行气动力展向相关性分析时,仅取气动力均匀分布段进行计算,即S7~S11,最大展向距离为540 mm,Lmax/D等于9。
2 实测气动升力及其相关性
2.1 实测涡激振动振幅特征
宽高比5∶1矩形断面竖向模态存在两个涡激振动锁定区间,第一个锁定区间的起振风速约为第二个锁定区间起振风速的一半,振幅小于第二个锁定区间。因电子压力扫描阀测试精度限制,本文仅进行了第二个锁定区间的涡振风洞试验。试验风速从3 m/s逐级增加到5.5 m/s,涡振竖向和扭转振幅随风速的变化如图3所示。不同风速下对应的结构竖弯和扭转无量纲振幅如表2所示,表中,U为来流风速,Ur为折减风速,Ur=U/(fD),A为某风速下结构稳态振动幅值。由图3和表2可知:1)结构发生了明显的竖向涡激振动,未出现扭转振动;2)最大无量纲振幅达到0.043,对应的折减风速为11.41。
2.2 实测气动升力特征
通过对实测截面风压进行积分得到气动升力系数CL(t),计算公式如下:
式中 Np为截面测点个数,Np=32;pi为第i个测点风压;li为第i个测点对应的有效计算长度;αi为第i个测点表面切线方向与来流风速方向的夹角,上、下表面分别对应0°,180°。
风洞试验实测气动升力系数标准差随风速的变化特征如图4所示。在锁定区间内,气动升力系数标准差在起振阶段达到最大,此后,随着风速的增大,虽然结构振幅增大,但是气动升力系数标准差反而减小,最小值仅为静止状态的一半。起振阶段U5风速和最大振幅对应风速U11的实测气动升力时程及其功率谱如图5所示。
2.3 气动力展向相关性
将展向位置x处实测气动力时程表示为C(t,x),位置x1和x2处气动力的展向相关系数为:
式中 E[·]为对时间变量求均值计算符。
对于固定模型或者未发生频率锁定的气动力,采用指数型函数能较好地拟合实测气动力展向相关特征,对于锁定区间内气动力,Ricciardelli等[11]提出的指数加常数型函数能较好地拟合实测气动力展向相关特征,因此,实测气动力的展向相关函数可以表示为:
式中 s为展向间距;a为相关系数,对于固定模型或者未发生频率锁定的气动力,a1=1,a3=0。
与Ricciardelli等[11]提出的公式略有不同的是,本文对公式(3)常数项也进行了拟合,即对a1,a2和a3均进行了拟合,而Ricciardelli等[11]提出的公式中因设定a1+a3=1,只需要拟合两个系数。
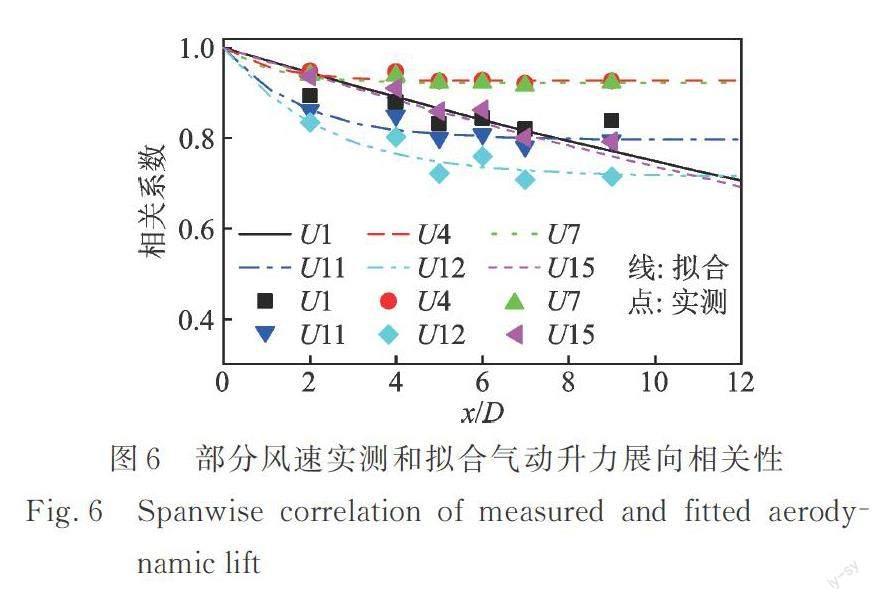
对实测气动力展向相关特征按照公式(3)进行了拟合,部分风速实测气动升力展向相关特征以及拟合函数曲线如图6所示。拟合气动升力展向相关函数的各系数如表3所示。在锁定区间外,即U1,U13~U15风速,展向相关函数的常数项a3=0,指数项系数a1=1,表征相关长度的a2处在35左右,与已有的固定模型气动力展向相关特征基本相符。而在锁定区间内,a2值在1.5左右,类似于随机噪声的相关性。
在锁定区间内,气动力展向相关强度变化规律与气动升力均方根变化规律相同,气动升力的展向相关强度并不随着涡振振幅增大而增大,振幅最大处,相关性反而最弱。
在锁定区间内,实测气动升力展向相关强度随着振幅增加而呈现减小的趋势,这与当前对展向相关性的认识不相符。该规律研究在多项研究成果中体现。本文接下来将对其进行分析。
3 气动力展向相关性分析
3.1 实测气动力展向相关函数建模
运动状态钝体断面上的气动力主要包括两部分:(1)运动诱发气动力,即自激力,因结构振动迫使流场规则变化而产生,与结构运动状态有关;(2)结构尾流区旋涡脱落产生的气动力,即涡脱气动力,该力频率一般满足斯特劳哈尔数规则。
根据Scanlan等[23]的气动自激力理论,自激力CO(t,x)是结构振动位移和速度的函数。卡门涡脱气动力的频率虽满足斯特劳哈尔数规则,但是,其幅值和相位具有随机性。实测气动力除了自激力和卡门涡脱气动力,还包括了测试噪声、来流风的湍流和模型外形不平顺等因素引起的气动噪声,这些噪声均具有随机的特征,将卡门涡脱气动力与噪声归类为随机气动力CS(t,x),则实测气动力CT(t,x)可以表示为:
节段模型振动是刚体振动,各截面的竖向振动位移相同,故自激力展向完全相关,即Ro=1。随机气动力的展向相关函数用指数函数描述。根据随机振动基本原理和展向相关性计算公式,且假设自激力与随机气动力相互独立,可得节段模型运动状态实测气动力的展向相关函数为:
且存在关系式:
式中 aS和aO分别定义为随机气动力和自激力占实测气动力的能量比。
公式(5)经适当变换,与Ricciardelli等[11]提出气动力展向相关函数完全相同。由公式(5)可知,运动状态节段模型上实测气动力的展向相关性由随机气动力和自激力各自的展向相关性特征、两者之间的相关性特征和各自的能量比决定。随机气动力能量比越小,自激力能量比越大,实测气动力展向趋向于完全相关。
3.2 实测涡激力展向相关性特征
矩形断面钝体结构的涡激振动可以分为两类[20]:运动诱发涡激振动和卡门涡脱诱发涡激振动。运动诱发竖向涡激振动的起振风速为:
式中 N为实数,N=1。
卡门涡脱诱发涡激振动的起振风速为:
式中 St为斯托罗哈数。
对于宽高比5∶1矩形断面,运动诱发和卡门涡脱诱发涡激振动的起振折减风速分别为8.4(N=1)和9.1(St=0.11)。因两类涡振的起振风速接近,当其发生涡激振动时,运动诱发气动力和卡门涡脱气动力具有相同的频率,无法分离,因此,实测气动力中可能同时包括这两类气动力,或者一类充分发展的同时抑制另一类的出现。不同类型诱发的涡激振动气动力特征不同,展向相关性也不同。
运动诱发气动力和卡门涡脱气动力均具有窄带特征。不考虑涡激力的倍频成分,采用带通的方法从实测气动力中分离了涡激力和随机气动力。本试验中,结构涡激振动频率约7 Hz,采用带通频率为[6,8] Hz的带通滤波方法从实测气动力中分离出渦激力和随机气动力。锁定区间内,部分风速分离出的涡激力展向相关性以及实测气动力展向相关性如图7所示。分离出的涡激力展向基本完全相关。因此,理论建模中,自激力(涡激力)展向完全相关的假设是正确的。
3.3 实测随机气动力展向相关性特征
随机气动力的能量比以及展向相关性也是影响实测气动力展向相关性的重要因素。
对比公式(3)和(5)可知,通过展向相关特征拟合获得的展向相关函数的系数a1与aS意义相同,即为随机气动力占实测气动力的能量比。通过对实测气动力进行带通滤波信号分解,分离出随机气动力,计算了随机气动力的能量比,通过信号分解得到的随机气动力能量比aS与通过展向相关函数拟合得到的随机气动力能量比a1的对比如图8所示。在锁定区间内,两者基本相符。
通过信号分解获得的随机气动力均方根以及根据拟合的a1和实测气动力均方根计算得到的随机气动力均方根如图9所示。在锁定区间内,两者也基本相符,实测随机气动力均方根基本保持不变。
3.4 讨论与分析
假设实测运动状态节段模型上实测气动力由完全相关的自激力和不完全相关的随机气动力组成。通过展向相关性理论分析,得出实测气动力展向相关性可以用指数加常数型函数描述。指数项系数表征随机气动力占实测气动力的能量比,常数项系数主要与涡激力的能量比相关,指数项系数与常数项系数之和为1。
通过对锁定区间内节段模型上实测气动力进行分解,分离出涡激力和随机气动力。在锁定区间内,实测涡激力在展向基本完全相关,实测随机气动力不完全相关,各风速实测随机气动力的均方根基本相同。
采用无约束的指数项和常数项系数拟合了实测气动力展向相关函数。拟合的指数项系数a1与实测随机气动力能量比aS基本相符,拟合的指数项系数与常数项系数之和等于或者极其接近于1。这些表明理论推导展向相关函数能正确表征实测气动力展向相关性,各系数物理意义解释正确。
在锁定区间内,随机气动力均方根基本不变,而实测气动力在起振阶段达到最大,此后,随着风速的增大而不断减小。因此,随机气动力的能量比在起振阶段最小,此后,随着风速的增大而不断增大,最终导致实测气动力展向相关性表现为:在锁定区间内,实测气动力在起振阶段相关性最强,随着风速的增大,结构振幅虽增大,但是相关性反而减弱。
本文试验在均匀流场中进行,湍流度小于0.5%。而实际工程结构处于湍流场中。当结构在湍流中发生涡激振动时,实测气动力中,与湍流相关的抖振力成分将增大,会导致实测气动力的展向相关性降低。湍流是否影响运动诱发涡激力的展向相关性有待进一步通过试验验证。
4 总 结
论文通过实测气动力展向相关函数理论建模和节段模型风洞试验,研究了宽高比5∶1矩形断面涡激振动锁定区间内的气动力展向相关特征,研究结果表明:
(1)在宽高比5∶1矩形断面节段模型涡激振动锁定区间内,实测气动力由完全相关的涡激力和不完全相关的随机气动力组成,展向相关性符合指数加常数型函数。指数项系数表征随机气动力占实测气动力的能量比。指数项系数与常数项系数之和为1。
(2)在锁定区间内,实测随机气动力均方根基本不变,实测气动力均方根在起振阶段最大、随着风速增加而减小,导致实测气动力展向相关性表现为起振阶段最强、随着风速增加而减弱。
参考文献
1赵林, 刘丛菊, 葛耀君. 桥梁结构涡激共振的敏感性[J]. 空气动力学学报, 2020, 38(4): 694-704.
ZHAO Lin, LIU Congju, GE Yaojun. Vortex-induced vibration sensitivity of bridge girder structures[J]. Acta Aerodynamica Sinica, 2020, 38(4): 694-704.
2Li Hui, Laima Shujin, Zhang Qiangqiang, et al. Field monitoring and validation of vortex-induced vibrations of a long-span suspension bridge[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2014, 124: 54-67.
3刘志文, 沈静思, 陈政清, 等. 斜拉索涡激振动气动控制措施试验研究[J]. 振动工程学报, 2021, 34(3): 441-451.
LIU Zhiwen, SHEN Jingsi, CHEN Zhengqing, et al. Experimental study on aerodynamic control measures for vortex-induced vibration of stay-cable[J]. Journal of Vibration Engineering, 2021, 34(3): 441-451.
4李加武, 党嘉敏, 吴拓, 等. 径向基神经网络用于钢-混Π型梁原始断面涡振性能的预测[J]. 振动工程学报, 2021, 34(1): 1-8.
LI Jiawu, DANG Jiamin, WU Tuo, et al. Radial basis function networks used in prediction of vortex-induced vibration of Π-shape bridge-decks[J]. Journal of Vibration Engineering, 2021, 34(1): 1-8.
5胡传新, 赵林, 周志勇, 等. 流线型闭口箱梁抑流板抑制涡振机理研究[J]. 振动工程学报, 2020, 33(1): 1-11.
HU Chuanxin, ZHAO Lin, ZHOU Zhiyong, et al. Suppressing mechanism of spoilers on vortex-induced vibration around a streamlined closed-box girder based on characteristics of aerodynamics forces and flow field[J]. Journal of Vibration Engineering, 2020, 33(1): 1-11.
6華旭刚, 黄智文, 陈政清. 大跨度悬索桥的多阶模态竖向涡振与控制[J]. 中国公路学报, 2019, 32(10): 115-124.
HUA Xugang, HUANG Zhiwen, CHEN Zhengqing. Multi-mode vertical vortex-induced vibration of suspension bridges and control strategy[J]. China Journal of Highway and Transport, 2019, 32(10): 115-124.
7祝志文, 陈魏, 李健朋, 等. 多塔斜拉桥加劲索涡激振动实测与时域解析模态分解[J]. 中国公路学报, 2019, 32(10): 247-256.
ZHU Zhiwen, CHEN Wei, LI Jianpeng, et al. Field observation of vortex-induced vibration of stiffening cables in a multi-tower cable-stayed bridge with application of analytical mode decomposition[J]. China Journal of Highway and Transport, 2019, 32(10): 247-256.
8West G S, Apelt C J. Fluctuation lift and drag forces on finite lengths of a circular cylinder in the subcritical Reynolds number range[J]. Journal of Fluids and Structures, 1997, 11(2): 135-158.
9刘志文, 黄来科, 陈政清. 矩形断面主梁涡激振动气动力展向相关性试验研究[J]. 振动工程学报, 2017, 30(3): 422-431.
LIU Zhiwen, HUANG Laike, CHEN Zhengqing. Experimental study on spanwise correlation of aerodynamic forces of VIV of the rectangular section girder[J]. Journal of Vibration Engineering, 2017, 30(3): 422-431.
10刘小兵, 张海东, 王彦彪. 宽高比为5的矩形断面梁气动力展向相关性研究[J]. 工程力学, 2015, 32(S1): 50-54.
LIU Xiaobing, ZHANG Haidong, WANG Yanbiao. Study on spanwise correlation of aerodynamic force of rectangular cylinder with aspect ratio 5[J]. Engineering Mechanics, 2015, 32(S1): 50-54.
11Ricciardelli Francesco. Effects of the vibration regime on the spanwise correlation of the aerodynamic forces on a 5∶1 rectangular cylinder[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2010, 98(4): 215-225.
12劉小兵, 张海东, 王彦彪. 扁平箱梁涡激力的展向相关特性研究[J]. 工程力学, 2016, 33(S1): 239-243.
LIU Xiaobing, ZHANG Haidong, WANG Yanbiao. Study on spanwise correlation of vortex-induced forces on a flat box girder[J]. Engineering Mechanics, 2016, 33(S1): 239-243.
13刘志文, 龚慧星, 陈政清. 流线型箱梁断面涡激力展向相关试验研究[J]. 湖南大学学报 (自然科学版), 2017, 44(5): 80-87.
Liu Zhiwen, Gong Huixing, Chen Zhengqing. Experimental study on spanwise correlation of vortex-excited forces of a streamlined box girder[J]. Journal of Hunan University (Natural Sciences), 2017, 44(5): 80-87.
14Sun Yanguo, Li Ming, Li Mingshui, et al. Spanwise correlation of vortex-induced forces on typical bluff bodies[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2019, 189: 186-197.
15Bruno L, Salvetti M V, Ricciardelli F. Benchmark on the aerodynamics of a rectangular 5∶1 cylinder: an overview after the first four years of activity[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2014, 126: 87-106.
16Wu Bo, Li Shaopeng, Cao Shuyang, et al. Numerical investigation of the separated and reattaching flow over a 5∶1 rectangular cylinder in streamwise sinusoidal flow[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2020, 198: 104120.
17Lin Siyuan, Wang Qi, Nikitas Nikolaos, et al . Effects of oscillation amplitude on motion-induced forces for 5∶1 rectangular cylinders[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2019, 186: 68-83.
18Nguyen D T, Hargreaves D M, Owen J S. Vortex-induced vibration of a 5∶1 rectangular cylinder: a comparison of wind tunnel sectional model tests and computational simulations[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2018, 175: 1-16.
19Li Mingshui, Li Shaopeng, Liao Haili, et al. Spanwise correlation of aerodynamic forces on oscillating rectangular cylinder[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2016, 154: 47-57.
20Matsumoto M, Yagi T, Tamaki H, et al. Vortex-induced vibration and its effect on torsional flutter instability in the case of B/D=4 rectangular cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6-7): 971-983.
21温青, 华旭刚, 池俊豪, 等. 端部条件和长宽比对矩形断面节段模型涡激振动的影响[J]. 振动工程学报, 2020, 33(4): 653-659.
WEN Qing, HUA Xugang, CHI Junhao, et al. Effect of end conditions and aspect ratios on vortex-induced vibration for a rectangular sectional model[J]. Journal of Vibration Engineering, 2020, 33(4): 653-659.
22温青, 池俊豪, 华旭刚, 等. 端部条件和展弦比对矩形断面节段模型气动力特征的影响[J]. 实验流体力学, 2020, 34(4): 36-43.
WEN Qing, CHI Junhao, HUA Xugang, et al. Effects of end condition and aspect ratio on aerodynamic properties of rectangular sectional model[J]. Journal of Experiments in Fluid Mechanics, 2020, 34(4): 36-43.
23Scanlan R H, Tomko J J. Airfoil and bridge deck flutter derivatives[J]. Journal of the Engineering Mechanics Division, 1971, 97(6): 1717-1733.
Spanwise correlation of aerodynamic forces in the lock-in region of VIV for 5∶1 rectangular cylinder
WEN Qing 1,2 ?LONG Hang 1HUA Xu-gang 2 ?CHI Jun-hao 1SUN Hong-xin 1
1. Hunan Provincial Key Laboratory of Structures for Wind Engineering and Vibrational Control, College of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China;
2. Key Laboratory for Wind and Bridge Engineering of Hunan Province, Hunan University, Changsha 410082, China
Abstract The spanwise correlation of vortex-induced forces (VIFs) is necessary to accurately predict vortex-induced vibration (VIV) amplitude of three-dimensional flexible structures. In this paper, the properties of aerodynamic spanwise correlation in the lock-in region are studied via theoretic modelling of aerodynamic spanwise correlation function and wind tunnel tests of VIV for the 5︰1 rectangular sectional model. The results show that in the vortex interval, the measured aerodynamic force consists of fully correlated self-excited force and incompletely correlated random aerodynamic force. The spanwise correlation can be described by exponential function and a constant, the exponential coefficient denotes the energy ratio of random aerodynamic force to measured aerodynamic force, and the sum of the exponential coefficient and the constant is equal to 1. The root mean square of measured aerodynamic lift is tend to be the stronger in the onset stage of VIV, but decreases with the increase of wind speed. The root mean square of random aerodynamic force seem to be identical. Therefore, the spanwise correlation of measured aerodynamic force in the onset stage is tend to the stronger than that in the following stage.
Keywords vortex-induced vibration; aerodynamic force; spanwise correlation; rectangular section
