对称的算式

◎马济敏

在学习“两位数乘两位数”时，我们除了要学会计算之外，还要去探讨乘法中一些有趣的规律，从而更好地掌握乘法的计算方法。比如，比较下面这些乘法算式的乘积，你有什么发现？

24×63= 42×36= 14×82= 41×28=

我们可以先算出乘积，再比较。

24×63=151242×36=151214×82=114841×28=1148

从结果可以看出：24×63=42×36，14×82=41×28。我们发现，24变成了42，63变成了36，14变成了41，82变成了28，即个位数字和十位数字交换，而乘积却不变。

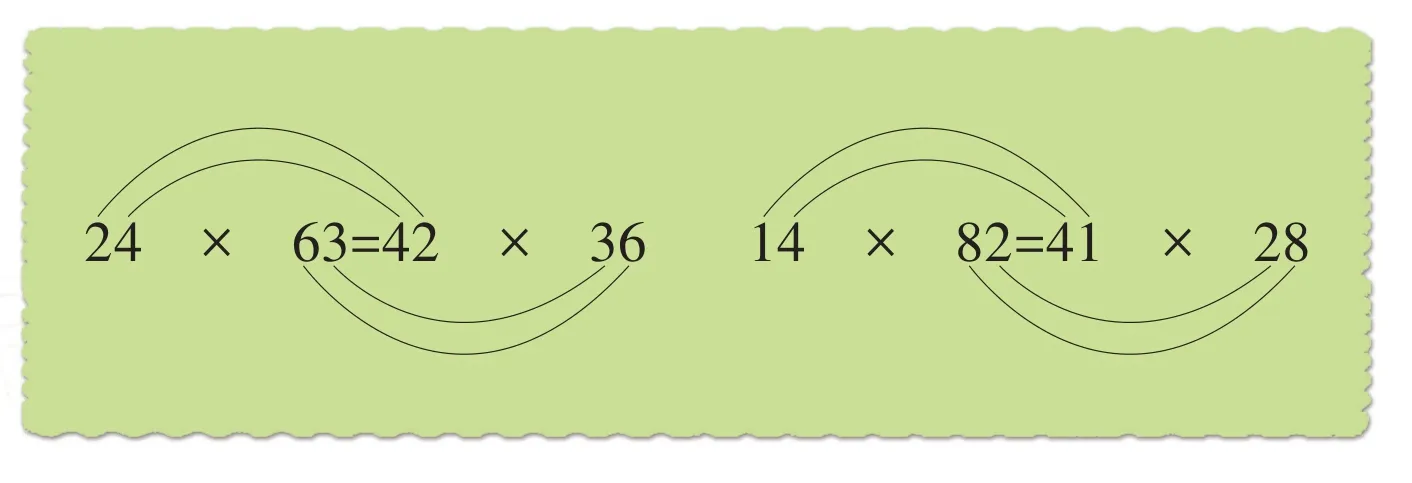
在两位数乘两位数的算式中，我们是否也能再“制造”出这样类似的算式呢？

我们先随便写一个试试，如：28×32=896，82×23=1886，结果不同；35×43=1505，53×34=1802……看起来，随便写是不行的。

我们再仔细观察，在算式24×63 中，2×6=12，4×3=12；在算式42×36中，4×3=12，2×6=12。也就是说，当两个数十位上数字的积等于个位上数字的积时，十位数字与个位数字调换，调换后两个数的乘积仍等于原来两个数的乘积。

例如：14×82=1148，1和4调换得到41，8和2调换得到28，41×28=1148，即14×82=41×28。

怎样来“制造”这样的算式呢？我们先写一组积相等的一位数算式，如2×9=18，3×6=18，那么是不是有23×96=32×69 呢？验算一下：23×96=2208，32×69=2208。耶！算式成立！

再来一组。3×8=24，6×4=24，组合成36×84，调换为63×48，连起来是36×84=63×48=3024。

类似的算式还有：1×4=2×2，1×6=2×3，4×4=2×8，6×6=4×9……利用这些关系，可以我们“制造”算式。

12×42=24×21=504，12×63=36×21=756，12×84=48×21=1008，13×62=26×31=806，13×93=39×31=1209，24×84=48×42=2016，26×93=39×62=2418

聪明的同学，你还能“制造”出更多类似的算式吗？如果是两位数乘三位数、四位数，有没有这样的规律呢？快拿起你的笔，写一写吧！