可动态校准的六维激励系统设计与实验研究

林星翰

（北京工商大学 人工智能学院，北京 100048）

0 引言

高精度航天器对微振动环境十分敏感[1]，因此需开展地面微振动试验，以测试航天器关键点对振动的响应特性，并检验隔振措施的有效性[2]。微振动试验一个至关重要的前提条件就是：在振源处精准施加激励。传统的激励实现途径是布置真实的活动部件，可以保证地面试验与在轨状态下的扰振特性一致，但是工程成本高昂，需要多个部门之间的协调，况且在航天器研制的早期阶段通常无法提供足够数量的真实活动部件。因此，有学者提出采用激振器输出等效的激励信号代替真实的活动部件，这就要求激振器的布局具有灵活性，能输出多维激励，并且激励信号的频谱与幅值能自由设置[3]。

国内外关于多维激励的研究以振动试验平台为主，平台的形式多采用Stewart 构型的并联机构，该技术已经发展得较为成熟，比如：美国MTS 公司[4]、Moog 公司[5]能够研制承载能力500 kg 以上、工作频率覆盖200 Hz 的振动设备；Zheng 等[6]结合主动控制算法使得Stewart 平台能够输出与预期一致的振动；徐振邦等[7]采用基于传递函数的控制方法将激励的实际值与目标值之间的误差控制在2%以内。振动试验平台还可以采用正交布置的结构形式[8]，将单轴作动器布置在水平和竖直两个方向上。然而，上述试验平台的结构尺寸非常大，运动机构复杂，并且主要用于在边界施加激励输入，难以在航天器的实际振源处施加激励。

通过缩小上述试验平台单轴作动器的结构尺寸可以提高激励点布置的灵活性。可以使用压电叠层[9]、音圈电机[10]或磁致伸缩器[11]进行作动器设计，其中音圈电机具有行程大、工作频带宽的优势，并且广泛应用于主动质量阻尼器，技术较为成熟。Park 等[12]采用3 个正交布置的带集中质量的音圈作动器代替动量轮，模拟其升速过程中产生的扰振力；林诺等[13]将6 个作动器安装到具有一定刚度的转接板上，输出200 Hz 以内的六维力/力矩。采用单体转接板转接全部作动器的形式仅能适应有限的应用场景，而多个作动器分布式布置的方式需要考虑传递环节柔性的影响，特别是在作动器与航天器本体之间存在隔振器的情况下。这就需要在使用前按照实际转接方式将作动器安装到测力台，并对作动器的输出特性进行标定。为了在实际应用过程中能够观测并校准输出的激励效果，需在作动器的活动质量上固定传感器，以测量其产生的惯性力，传感器的响应特性也需要进行标定。

本文设计可动态校准的六维激励系统，用于替代真实活动部件在航天器的任意位置施加准确的激励力/力矩。首先建立六维激励系统的单个作动器的理论模型，并给出多个作动器的分布条件；考虑到装置可能存在的安装误差以及被测试结构的柔性，还需要设计标定实验以确保整套模拟系统的准确性；继而详述激励系统的标定过程以及标定结果；最后根据标定结果分析作动器输出力的稳定性、不同作动器动力学特性的差异以及不同位置传递特性的差异。

1 六维激励系统工作原理

为产生六自由度的振动激励，须满足以下要求：1）可以在指定位置模拟扰振力，在没有星本体的情况下将模拟扰振信号直接施加到部件上；2）安装位置是可调节的，整个系统可根据使用对象的需要灵活调整，满足多种使用场景的需求；3）通过待激励结构提供的安装位置或工装固定到待激励体上，便于拆卸。

根据以上目标和要求，本文首先针对单台模拟源进行设计，得到能够符合要求的稳定的激励产生装置；然后组合成激励系统，使多台模拟源产生的激励能合成满足要求的六自由度扰振力/力矩。

1.1 单个作动器的理论模型

单个作动器的结构剖视图如图1(a)所示，包括音圈电机、传感器、膜簧、信号接口、芯轴组件以及壳体。其中音圈电机包括磁钢和线圈两部分。磁钢、传感器和芯轴组件共同构成作动器的惯性质量m，膜簧的法向刚度等效为k，作动器的阻尼记为c，则可以得到如图1(b)所示的作动器原理图。

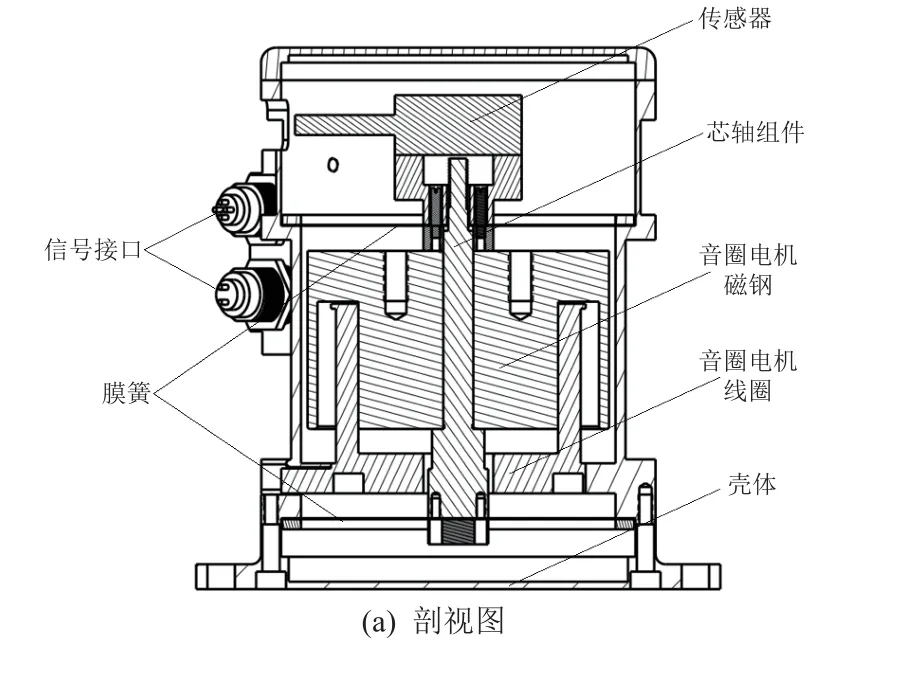
图1 单个作动器模型Fig.1 Model of an individual actuator

通过控制器对音圈电机施加模拟信号，音圈电机输出的安培力会驱动惯性质量做受迫运动。将安培力记为FA，惯性质量的位移记为X，通过壳体传递给安装基础的力记为F。FA与X之间的传递函数表达式为

因此，从输入力FA到激励力F的传递函数表达式为

传感器选用电容式加速度传感器。将惯性质量的加速度乘以质量系数之后，可以得到实际输出的激励力；将其与要求施加的激励力进行比较，以修正控制器施加的模拟信号，最终使实际输出的激励力等于目标值。作动器的关键参数及取值如表1所列。

表1 作动器的关键参数及取值Table 1 Key parameters and values of the actuator

1.2 多个作动器的分布条件

六维激励系统包含6 个单自由度作动器，分布如图2 所示，其中Ai表示第i个作动器的位置坐标，Fi表示第i个作动器的激励力。2 个作动器为1 组，激励力的方向互相平行；3 组作动器的激励力互相正交。为不失一般性，记F1和F2平行于x轴，F3和F4平行于y轴，F5和F6平行于z轴。

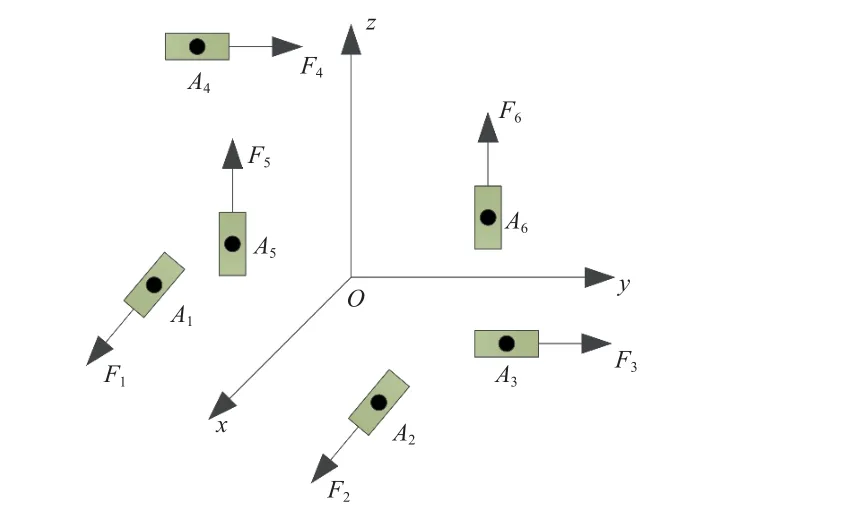
图2 6 个单自由度作动器的分布Fig.2 Distributions of six single degree of freedom actuators

作动器的系数矩阵B记为

六维力/力矩的目标值记为F，与每个作动器激励力之间的关系可以表示为

其中：F=[Fx,Fy,Fz,Mx,My,Mz]T；C=[F1,F2,F3,F4,F5,F6]T。

若要使得六维力/力矩可以取到任意值，则系数矩阵B应满秩，等价于

式(6)表示作动器的位置约束条件，物理含义为：每组作动器输出力矩的矢量方向由空间位置唯一确定，3 个力矩矢量不能共面，否则输出力矩会缺失沿共面法向方向的自由度。

上述公式均建立在作动器输出的激励力矢量方向与芯轴组件轴线重合的理想化前提下，而实际工程应用中，由于重力、加工误差和装配误差等因素的影响，总会产生垂直于芯轴组件轴线的力分量，这就需要修正系数矩阵的每一列，位置约束条件也会更加复杂。

此外，本研究中各作动器采用独立转接的方式，取代文献中采用的高刚度整体转接的方式，以便实现灵活布置。在这种情况下，每个作动器到星本体结构界面的传递特性会有差异，主要表现为幅值和相位特性的不同。

多个作动器组合布控时，为排除上述非理想输出特性和非一致传递特性的影响，有必要进行组合标定。

2 标定方法

标定分为单个作动器动力学特性的标定和多个作动器组合输出特性的标定两部分，其中：单个作动器动力学特性的标定主要是确定控制器施加的模拟信号到作动器输出的激励力之间的比例系数α，同时校准传感器的标称灵敏度；多个作动器组合输出特性的标定主要是标定每个作动器输出的激励力到测力台的传递函数的幅频特性和相频特性。

式中：V为作动器接收的模拟信号，本文选择电压信号控制作动器，通过改变电压的频率和幅值来改变激励力的频率和幅值特性；比例系数α为作动器对模拟信号的灵敏度系数，与作动器的电感特性、电阻特性以及放大电路的特性有关，因此不同作动器的α存在差异，即使是同一作动器，α也会随着激励频率的变化而变化。

对于单个作动器的标定，为了减小重力因素的影响，将作动器竖直安放于测力台进行标定，标定现场如图3 所示。对于多个作动器的组合标定，需要先将多个作动器按照实际转接方式与测力台连接，如图4 所示。

图3 单个作动器标定Fig.3 Calibration of an individual actuator

作动器标定的步骤如下：

1）将作动器1 安装至测力台，连接相关采集通道；

2）控制器生成单频正弦控制信号并发送给作动器，控制信号频率设置见表2，幅值设为0.02 V；

表2 标定过程中的控制信号频率设置Table 2 Control signal frequency setting during calibration

3）同时采集测力台和传感器的响应数据；

4）重复步骤2）、3），完成同一激励条件下的3 次采样；

5）改变控制信号频率，然后重复步骤2）～4），直至完成作动器1 全部频率设置下的标定；

6）更换为作动器2，重复步骤2）～5），完成作动器2 全部频率设置下的标定；（以此类推，完成全部6 个作动器的单独标定）

7）将6 个作动器按照图4 所示的方式转接至测力台；

8）选择一个单频正弦控制信号，6 个作动器依次单独工作在该控制信号下，获取测力台的响应；

9）令6 个作动器同时工作在该控制信号下，获取测力台的响应。

3 标定结果分析

3.1 同一作动器输出的稳定性

由于单个作动器在每个设置频率下都进行了3 次标定，统计作动器输出激励力（测力台测试结果）、传感器测试结果的均值和标准差，以评估同一作动器输出的稳定性。以作动器1 为例，如图5 所示，测力台测试结果的标准差不超过0.03 N，而传感器测试结果的标准差在0.05～0.40 N 范围内，观测结果可以作为动态校准的参考值。假设不同频率下的输入力一致，用式(3)描述的单自由度系统进行仿真，同时代入表1 所列的参数值，可以得到作动器输出激励力的仿真结果，如图5 中的绿色虚线所示，可以看出在某些频率条件下实际值与仿真值间存在一定的差异，这既与比例系数α的幅频特性有关，又与加工装配的非理想干扰（如膜簧存在局部变形）以及音圈电机的本底噪声等有关。

图5 单个作动器输出激励力标定结果Fig.5 Calibration results of individual actuator output excitation force

3.2 不同作动器输出特性的差异

对比6 个作动器在表2 中所列的激励频率（f1～f8）下分别计算得到的比例系数α，以评估不同作动器输出特性的差异，结果如图6 所示，可以看出α基本保持一致，差异不超过10%。

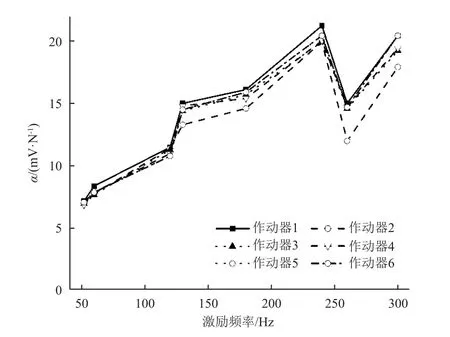
图6 不同作动器的输出比例系数Fig.6 Output ratio coefficient of different actuators

3.3 不同位置作动器传递特性的差异

激励频率为130 Hz 时，不同位置的作动器单独工作，由测力台测得的激励力/力矩幅值和相位特性如图7(a)和图7(b)所示。根据幅值和相位可以构造形如Aeiφ的复数矩阵，维数为6×6，即控制信号到六维力/力矩的传递矩阵。

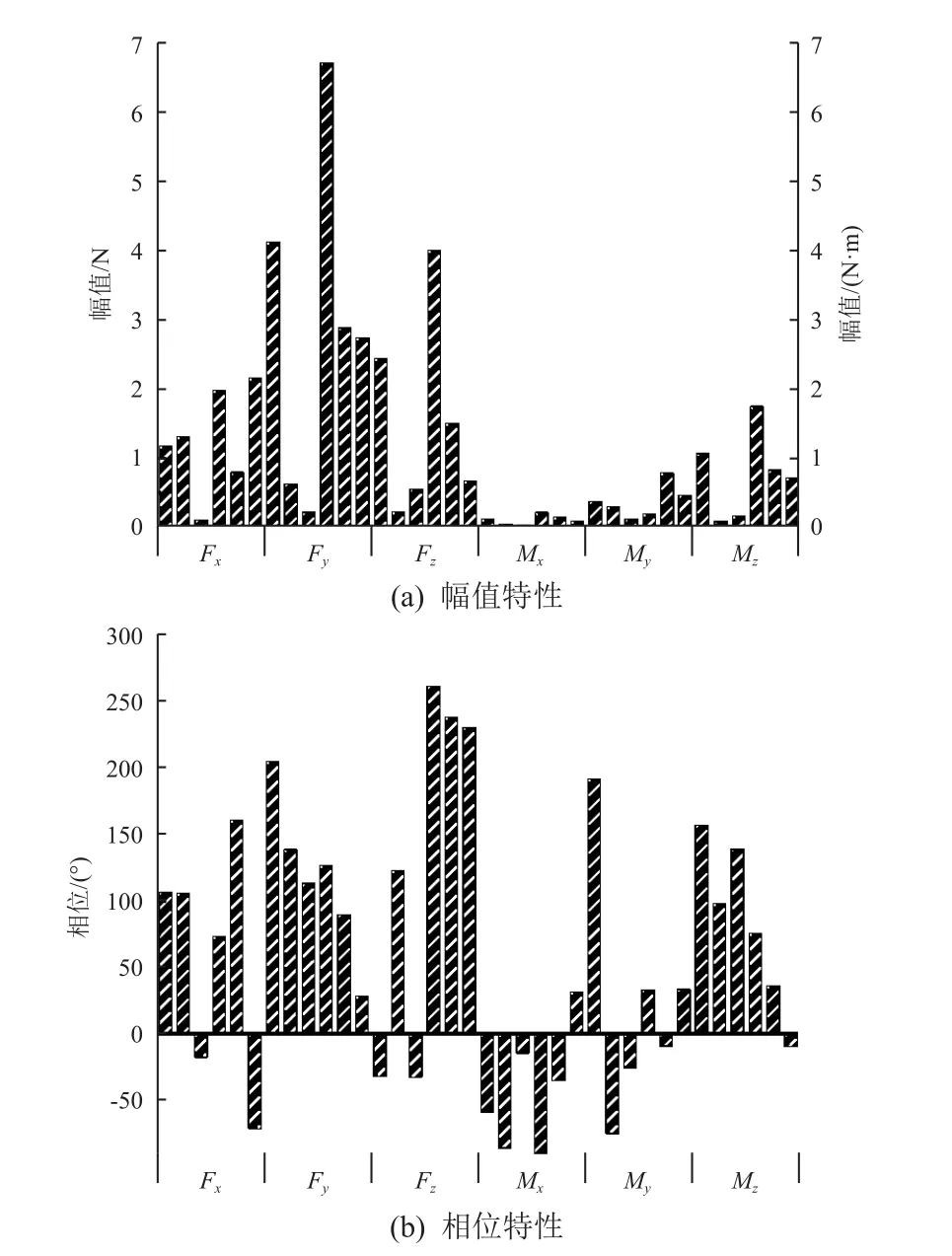
图7 不同位置作动器的传递特性Fig.7 Transfer characteristics of actuators at different positions

根据不同作动器之间的差异低于10%，可以认为不同位置的激励测得的幅值和相位差异由作动器与星本体之间的传递环节决定。由于控制信号的相位仅能设置为0°或180°，当已知目标力/力矩，求解每个作动器需要施加的控制信号时，需要先设置相位约束条件，然后采用试凑法，检验每种作动器控制信号的组合所产生的实际激励效果，最后从中挑选出最接近目标值的1 种组合。

4 结束语

本文设计了可动态校准的六维激励系统，可替代真实活动部件，在航天器地面微振动试验中模拟真实振源在航天器的任意位置施加准确的激励力/力矩：建立了六维激励系统的单个作动器理论模型以及多个作动器的分布条件；详述了激励系统的标定过程以及标定结果。结果表明：本文所设计的作动器的自校准偏差在0.4 N 以内；不同作动器之间输出特性的差异小于10%。

通过本文研究已初步实现设计目标，并委托第三方开展了力学环境试验和热真空试验，经验证满足空间环境使用要求，拟应用于我国新一代静止轨道成像卫星，目前卫星已进入工程研制阶段。