基于BP神经网络法的科创板企业价值评估

2023-07-06骆正清李梦可

会计之友 2023年13期

骆正清李梦可

【摘要】科创板上市企业具有高投入、缓收益、信息披露不完善等特点，运用现有价值评估方法对其进行评估存在数据缺乏和评估准确性不高的缺点，并且难以衡量科创板企业的成长能力。为了更加科学准确地评估科创板企业价值，通過分析影响其价值的因素，构建包含市场占有度、治理能力、资产结构、创新投入和EVA的价值评估指标体系，之后利用Spearman相关性分析和MIV值分析对指标体系进行约简，最后使用BP神经网络构建价值评估模型。结果表明：通过191条数据的训练仿真，基于BP神经网络的科创板企业价值评估模型预测准确度为82.93%，模型具有较好的适用性和可靠性。其中，EVA的相对影响度为23.69%，能有效反映科创板企业真实的价值创造能力。

【关键词】科创板企业；价值评估； EVA； BP神经网络

【中图分类号】 F234.3；F270 【文献标识码】 A 【文章编号】 1004-5937（2023）13-0019-08

一、引言

自2019年7月首批25家科创板公司挂牌交易以来，我国资本市场迎来了改革的新浪潮。目前，科创板上市公司数量已超500家，总市值超5万亿元。科创板主要服务于科技创新企业，向高精尖产业提供融资新渠道、注入发展新动能，这是我国不断探索实现科创企业快速发展和科技产出资本化的成果。相比于已有板块，科创板实行注册制，上市条件增加了对市值的要求，定价方法采用市场化询价的IPO定价法，但是多数上市企业对市值的估算方法披露不完善，定价的主观性也较强。因此，科创板上市企业的价值评估成为经营者和投资者等利益相关方关注的焦点，科学合理地评估科创板企业价值对促进我国高科技产业持续发展和证券市场有序运行具有重要作用。

然而，科创板企业高研发、缓收益和深潜力的特点使得传统估值方法难以准确衡量其未来盈利能力；信息披露不完善和价值评估适用的操作指引不明确，增加了新估值方法评估的主观性；市场数据缺乏和公司价值波动幅度大，价值评估结果的准确性难以提高[1]。目前，人工智能技术应用越来越广泛，不断有机器学习的方法应用到企业价值评估中[2]，价值评估结果的准确性得以提高，其中BP神经网络法具有三类优点：对数据要求不高，即分析的样本数据都是企业已披露并可获取的数据；自学习，即通过信息正传播和逆反馈不断调整参数，降低模型输出值和真实值的误差；拟合效果好，即输出误差达到目标范围，模型才会迭代终止，其应用较为广泛[3]。因此，BP神经网络法可以解决现有方法面临的评估数据不足和评估结果准确性不高的问题，结合对初选指标的约简分析，该方法在精简指标体系的同时又能够提高价值评估的准确度。

二、文献回顾

（一）科创板企业价值评估指标

准确评估科创板企业价值，需要选择科学适用的评估指标，选取指标的结果要避免两种极端：一是使用传统方法重视财务指标作为一切的基础，二是无端夸大企业未来发展空间，价值评估要能准确体现其科技创新形成的经济成果[4]。国内已有对科创板企业价值评估的研究多是分析企业的特点和价值影响因素，进而建议针对性地增加新指标。在行业市场方面，科创板上市的判断条件之一就是企业对所处行业的影响度，所以估值方法中要加入行业市场因素[1]；在资产结构方面，相比于传统企业，科创板企业的流动资产占比大、固定资产占比小[5]；在企业治理方面，科创板企业普遍“小而精”的特点要求其具有更高的治理能力，治理结构要能避免可能出现的投资者控制权弱的问题[6]；在科创属性方面，研发创新是科创板企业创造价值的源动力，关于对其科创属性的评价指标，由原来的“3+5”变成现在的“4+5”，即在研发投入、发明专利和收入增长的基础上新增了研发人员比例指标，学者们也一致认为研发投入强度和研发团队规模可以较好地解释科创板企业的创新发展能力[7]。

关于科创板企业价值评估指标的已有文献表明，相关学者从行业市场、企业资产结构、治理能力和科创属性角度提出了不同的建议，以实现更科学全面地衡量科创板企业价值。但也存在有待研究之处：一是现有文献大多从理论角度提出建议，指标是否切实可行还没有得到实践检验；二是现有研究多是对科创板某一具体公司的价值评估，评估指标有较强的针对性；三是对于反映科创板企业真实价值和未来盈利能力的指标还不够准确全面。

（二）科创板企业价值评估方法

为了探索适用于科创板企业的价值评估方法，本文总结了国内外选择和应用评估高新技术企业价值方法的研究。左庆乐等[8]提出高新技术企业价值评估的真正对象是未来获利能力，是企业可持续发展的能力。成本法注重企业中各单项资产的价值加总，市场法依据可比公司的数据，收益法取决于未来每期现金流和合理的折现率，这三种传统价值评估方法难以准确衡量高新技术企业的潜在收益能力，不适用于评估科创板企业价值。

期权定价模型解释了高新技术企业前期微利但高股价的状态，期权能体现企业未来的发展机遇、测度企业的机会价值[9]，所以期权定价法成为高新技术企业价值评估的全新技术。依赖于期权的假设，期权定价法更强调未来价值的折现，加上参数的选择具有主观性，所以其对企业现有基础上的获利能力评估不足。汤姆等[10]提出，高新技术企业价值评估最好的方法是折现现金流量法。与期权定价法相比，该方法是在企业现有价值的基础上评估未来现金流并折现，所以其评估企业现有经营业务价值的结果更准确。期权定价法强调企业未来的价值，折现现金流量法可以准确评估企业现有基础上的获利能力，而且后者所需参数适用于前者，所以早期的高新技术企业价值评估多是采用了两者结合的方法，评估结果的准确性也更高[11]。随着期权定价法应用增多，有学者为了提高其适用性和准确性，提出了改进评估指标或改善模型的方法[9]，还有学者提出EVA估值法[12]、级数突变法[13]等用于评估高新技术企业价值的新方法。

但是，现有企业价值评估方法应用于科创板企业存在一定的局限性，一是科创板企业历史数据少，用于价值评估的参考数据不完善，使得已有方法在计算中存在评估参数选择不准确或者获取困难的问题；二是影响科创板企业潜在盈利能力的因素较多，但是考虑过多因素会增加计算复杂度，从而降低评估准确度。

随着信息技术的发展应用，部分学者开始运用深度学习算法中的神经网络法评估高新技术企业价值，该方法可以减少评估数据的处理时间，提高评估结果的精确度[14]。神经网络方法评估企业价值的基本思路是：首先分析影响企业价值的因素，构建评估指标体系；然后获取样本数据，确定网络的输入层和输出层；最后通过神经网络对样本数据训练仿真，构建价值评估的神经网络模型。在实际应用中，合理完善的指标体系对构建准确可靠的神经网络模型具有重要影响，模型训练过程还需要不断调整参数以提升学习速度、降低输出误差值、提高模型拟合度。其中，BP神经网络是应用最多和最成功的神经网络[15]，它模拟人工神经系统，利用自学习过程来拟合变量间的非线性关系，理论上适用于评估高新技术企业的价值。

综上所述，本文认为能够科学有效地衡量科创板企业的成长性、不依赖历史数据且适用于科创板整体企业的价值评估方法是：以企业现有披露指标为基础，构建价值评估指标体系，之后约简指标以消除信息冗余，最后利用BP神经网络法构建价值评估模型。

三、科创板企业价值评估指标体系构建

（一）评估指标初选

科创板企业的科创属性凸出，对其价值评估要能准确体现其科技创新形成的经济成果[4]。参考科创板上市标准并结合已有文献，尽可能做到选取全面且精简的指标，最终本文在选择偿债能力、经营能力、盈利能力、发展能力4个基本指标和企业规模的基础上，增加了市场占有度、治理能力、资产结构、创新投入和经济增加值5个指标，构建了包含10个基本指标，25个具体指标的初选指标体系，如表1。

其中，市场占有度用市场占有率来衡量，主要因为市场占有率会影响企业的竞争性，而竞争优势有助于提升技术密集型上市公司的盈利能力，进而影响企业价值[16]。治理能力选择企业的独立董事比例，因为合适的独立董事比例有利于公司绩效的提高[17]。资产结构选择固定资产比例和无形资产比例，主要因为固定资产是企业用于生产材料的重要体现，无形资产是科技创新发展的内在驱动力，两种资产通过影响企业的资金流、资源占用和生產销售等影响企业的整体发展情况[5]。创新投入选择研发投入强度和研发人员比重，因为高研发企业通常能通过吸引投资者关注和改善企业经营业绩来提升企业的资本市场表现[18]。

本文创新性地增加了EVA指标以更准确地反映科创板企业的潜在盈利能力。首先，科创板允许未盈利或微利状态企业上市，EVA指标通过会计项目调整能反映真实经营业绩[19]，可以警惕企业出现资产泡沫和“脱实向虚”的风险；其次，EVA是企业的经济增加值，可以衡量企业的成长性，弥补传统财务指标体系的不足[20]；最后，EVA指标在一定程度上激励管理者关注长期价值创造，提升企业核心竞争力，衡量企业可持续发展潜力[21]。所以，引入EVA对于评估科创板企业的真实业绩和发展能力具有关键作用。

（二）初选指标数据计算

本文研究的样本数据来自于国泰安数据库和上市公司年报，样本企业是截至2020年底科创板的232家上市公司，指标数据是232家公司的年度数据，在具体计算中有部分调整。输入指标是表1中的25个具体指标，输出指标是样本企业在2020年12月31日公布的市值。其中，市场占有率是该企业与科创板232家上市企业的营业收入比，独立董事比例是企业独立董事人数和股东总比值，EVA指标的计算公式如下：

EVA=税后营业净利润-本期资本占用额×加权平均资本成本

其中，

税后营业净利润=营业利润-所得税费用+（1-所得税税率）×（财务费用-营业外收入+营业外支出+研发费用-非经常性损益）+递延所得税负债增加-递延所得税资产增加+各项准备金本期资本占用额=平均{短期借款+交易性金融负债+一年内到期的非流动负债+长期借款+应付债券+长期应付款-无息流动负债-视同无息流动负债-在建工程+递延所得税负债-递延所得税资产+所有者权益+各项准备金+（营业外收入-营业外支出）}×（1-所得税税率）

加权平均资本成本选用资本资产定价模型：

WACC=KSS/（S+D）+KDD/（S+D）（1-T）

其中，KS=Rf+β（Rm-Rf）

计算EVA的上述公式中有调整的数据包括：部分企业期初资本占用额是其上市后首次披露的数据，这是因为这些企业对2020年的期初数据披露不完善；加权平均资本成本中的无风险利率Rf采用人民银行一年期定期存款利率1.50%；β是232家企业中67家已公布β数据剔除最大和最小值后的平均值1.55；市场风险溢价（Rm-Rf）是2020年我国GDP增长率2.30%；债务资本成本KD是一年期短期贷款利率4.35%。剔除数据缺失值，最终得到191家样本企业和191条样本企业的数据。

（三）指标约简

考虑到科创板企业价值评估的初选指标存在一定的信息冗余，这里运用Matlab软件通过Spearman相关性分析和MIV值分析对构建的初选指标体系进行约简处理，约简依据是输入指标对输出指标相关度和影响度的大小。Spearman相关性分析得到输入指标和输出指标间的相关系数，根据系数值范围剔除弱相关因素，对输入指标做出初步筛选[22]，在此基础上，MIV值法分析初步筛选指标对输出指标的平均影响值，然后根据相对贡献率选取影响度高的指标[23]，构建最终指标体系。相关性分析和MIV值分析结合使用，提高了指标的精简性，保证了输入层指标的可靠性。为了消除数据大小和单位对筛选过程的影响，本文运用Matlab软件中的mapmaxmin函数先将191条数据归一化到[-1，1]，然后对归一化后的数据进行分析，归一化的公式如下。

1.Spearman相关性分析

Spearman相关系数是一种根据数据间相关系数大小测度相关度的统计量，在经济数据分析中的应用越来越广泛。该方法对数据要求不高，只要两个变量是成对的或者是连续观察得到的即可，而且相较于Pearson相关性和Kendall相关性，Spearman相关性更适用于分析具有非线性关系的数据。Spearman的运算思想是：把数列x={x1，x2，…，xn}按升序或降序排列得到顺序数列a={a1，a2，…，an}，x内每个元素在a中的位置为xi的秩次为Ri，得到x对应的秩次数列R，同样数列y={y1，y2，…，yn}得到对应的秩次数列S。将其代入Spearman等级相关系数公式：

两列数据呈正相关时θ是正数，呈负相关时θ是负数，θ的绝对值越大，变量的相关性越强。

借鉴文献应用Spearman相关性分析结果来评价和筛选财务指标的做法[22]，本文运用Matlab软件计算归一化后的各输入指标和输出指标间的相关系数，之后根据相关系数值剔除小于20%的弱相关指标，初步得到如表2中的13个指标。这13个指标和科创板企业价值均呈正相关关系，相关系数在40%以上即紧密相关的指标有6个。其中，资产规模的相关系数为74.86%，营运资金为66.82%，归属于上市公司股东的扣除非经常性损益的净利润为57.48%，营业收入为55.85%，市场占有率为55.85%，EVA为55.62%。

科创板开板时间短，多数企业处于初创期或者成长期，拥有一定规模的资产才能保证其日常运营，而且从技术研发到成果应用，每个阶段都需要大量资金支持，所以资产规模和营运资金为企业实现盈利提供支撑；归属于上市公司股东的扣除非经常性损益的净利润是控股股东的收益，反映了投资科创板企业的业绩，营业收入直观反映了企业的经营业绩，这两个指标评估了企业的盈利成果；市场占有率是企业的市场份额，市场份额越大，竞争性越强，发展前景越广阔，而EVA是企业价值创造值，这两个指标均解释了企业的潜在盈利能力。相关性分析的结果体现了盈利实力、经营业绩和潜在盈利能力对科创板企业价值评估的影响，其中EVA的相关系数为55.62%，初步验证了EVA对评估科创板企业价值的可行性。

2.MIV值分析

MIV值是平均影响度，具体运算过程是：首先，神经网络利用训练集构建模型；其次，將训练集每个指标数据增加10%和减少10%作为新的样本数据；再次，运用构建的模型预测新样本得到预测值；最后，对预测结果的差值按样本数量计算平均值，得出每个指标的平均影响值。

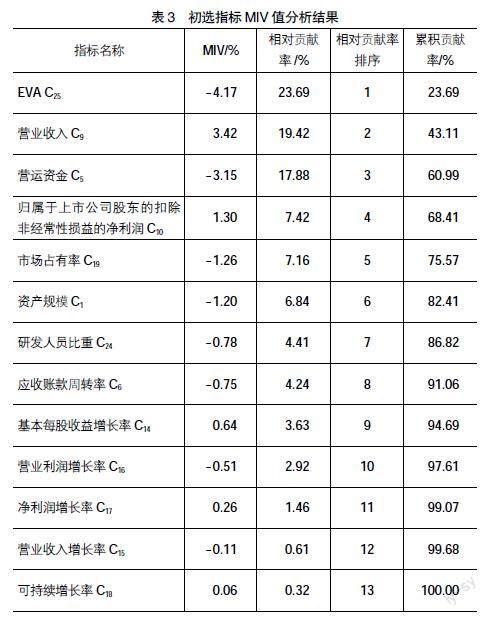
本文的分析过程是：（1）将191条归一化后的数据随机打乱顺序，运用BP神经网络对前8/10共150条数据构建模型；（2）利用构建的模型对表2中的13个指标进行MIV值分析，得到指标的平均影响度；（3）计算指标的相对贡献率，结果如表3。

相比于Spearman相关性分析，MIV值分析更深入，因为将样本数据增加10%和减少10%相当于扩大了样本规模，而且分析的依据是输入数据本身的变化对输出数据的影响。由表3可知，MIV值分析的最终结果是：13个指标中，净利润增长率、营业收入增长率和可持续增长率3个指标被剔除，排序最前的三个指标其相对贡献率均超过了10%。相对贡献率的具体结果是：EVA为23.69%、营业收入为19.42%、营运资金为17.88%。MIV值分析的结果也体现了盈利实力、盈利表现和潜在盈利能力对科创板企业价值评估的意义。其中，EVA的相对贡献率最大，进一步验证了EVA评估科创板企业价值的适用性。

从表3中选取相对贡献率大于2%即影响度较高的指标，最终构建包含10个输入指标的科创板企业价值评估指标体系如表4。总体上，科创板企业价值评估的指标包括了企业规模、偿债能力、经营能力、盈利能力、发展能力、市场占有度、创新投入和经济增加值8个基本指标；具体来看，8个基本指标又分别从企业自身经营、市场定位和未来发展能力反映企业价值；细分的10个具体指标既包含了一般企业价值评估的要素，又有反映科创板企业特点的要素如市场占有率、研发人员比重和EVA。最终表明，本文构建的指标体系对评估科创板企业价值具有可靠性。

四、科创板企业价值评估模型构建

（一）BP神经网络的基本原理

BP神经网络是一种通过反向传播进行深度学习的网络算法，模拟人脑神经系统，具有自学习的特点，模型的结构包含输入层、中间层和输出层，每一层有若干个神经元，其中中间层神经元的个数需要在模型训练中确定。自学习过程就是正传播和逆反馈的过程。正传播是上层神经网络的信息传播到下一层，直至最终输出层；逆反馈是输出层将误差结果反馈到第一层。自学习的目标是不断降低模型输出值和真实输出值之间的误差，BP神经网络会对输入指标随机设定初始权重，每一层之间会有激活函数通过不断调整拟合指标的非线性关系来局部调整误差。

（二）BP神经网络模型构建

1.数据归一化

本文最终的样本数据规模是191个企业、每个企业10个输入指标的191×10的矩阵。数据的大小和单位一定程度上会影响神经网络的学习效率，归一化后的数据可以提升学习速度和学习准确度，同时考虑到本文输入指标有负值，所以利用mapmaxmin函数将数据归一化到[-1，1]。

2.BP神经网络结构确定

三层结构的BP神经网络就可以拟合变量间的任何关系，且操作简便，所以本文的BP神经网络是三层拓扑结构。各层神经元个数是：输入层神经元10个，输出层神经元1个，隐含层神经元个数运用公式（ +a）（m是输入层神经元个数，n是输出层神经元个数，a是[1，10]的整数）确定范围在[5，14]，通过试错法得到隐含层神经元为12个时，模型的误差值最小、回归系数最高。所以，本文的神经网络是图1所示的10-12-1的拓扑结构，其中10个输入层指标对输出层神经元的相对贡献度如图2所示。

3.激活函数和训练函数确定

较常用的BP神经网络激活函数是Sigmoid函数，该函数又具体分为Log-Sigmoid函数和Tan-Sigmoid函数，其中Tansig函数能将数据映射到[-1，1]范围，所以本文选用此函数作为输入层到中间层、中间层到输出层的激活函数。BP神经网络的训练函数主要包括traingd、traingda、traingdx和trainlm函数，trainlm函数对于中等规模的BP神经网络有较快的收敛速度，是系统默认算法，所以本文选用此函数作为训练函数。

4.目标误差确定

设定不同的误差目标值，神经网络模型的拟合效果不同。对于相关度较高的指标，误差目标值会定义得较小，通常是10-6～10-4，相关度较低的指标，误差目标值一般是10-2。上述已对指标进行了Spearman相关性分析和MIV值分析的约简处理，所以本文设定的误差目标值是10-4。

5.迭代次数和学习率确定

本文样本数据规模小，迭代次数设置为1 000次。神经网络学习率的范围一般是0.0～0.9，较大或较小可能造成模型拟合不足或过拟合，所以本文通过试错法选取输出误差最小、学习时间最短和回归系数最高的学习率0.01。

（三）BP神经网络模型训练和仿真

本文运用Matlab软件对191×10的样本数据训练仿真。首先，运用randperm函数将191条数据随机打乱顺序，按照约8■2的比例选取前150条数据作为训练集，余下41条数据作为测试集。其次，运用BP神经网络对训练集训练，以构建模型。最后，利用构建的模型对测试集仿真预测，导出预测结果并和真实结果比对，计算相对误差。

训练的结果是，模型迭代终止时，误差值为0.0005，即构建的模型对测试集再预测的值和真实值之间的误差值为0.0005，并且在设定误差10-4范围内。模型的回归系数为0.8969，即10个输入指标对输出指标的相关度为0.8969，表明模型解释度较好。仿真结果如图3，本文计算的误差结果是，41条仿真数据中，相对误差值在15%（神经网络模型预测结果公认可以接受的误差范围是15%）以下的有34条数据，占比82.93%，所以模型预测结果的准确率为82.93%。有2条数据（第10、19条）预测结果偏差较大，和训练数据对比后归结为指标异常数据，余下39条数据（数据是归一化后的结果）的相对误差值如表5，其中，相对误差小于10%的数据有32条，占比82.05%，相对误差小于5%的数据有26条，占比66.67%。

五、研究结论与展望

本文在综合分析科创板企业价值影响因素的基础上，确定价值评估初选指标体系，对191家企业数据采用Spearman相关性分析和MIV值法进行指标约简，进而构建最终的输入层指标体系，最后运用三层BP神经网络对样本数据训练仿真构建模型，得出如下结论：

盈利实力、经营业绩和潜在盈利能力是影响科创板企业价值的三个关键要素。这三个要素均通过Spearman相关性和MIV值分析的指标约简结果以及构建的BP神经网络价值评估模型得到验证。

BP神经网络法适合科创板企业价值评估。本文样本数据是191×10，用于BP神经网络的学习建模属于小规模数据，最终，模型的回归系数是0.897、仿真准确度达到了82.93%，说明BP神经网络适用于科创板企业价值评估，不仅操作简便，评估结果也较为可靠。

EVA指标体现了科创板企业的价值创造能力。以往EVA多作为衡量企业績效的因变量，本文将其用作输入指标是为了体现科创板企业的真实价值和价值创造能力在其价值评估中的重要性。指标约简过程中EVA的Spearman相关系数是55.62%、相对贡献率是23.69%，这说明EVA可以作为科创板企业价值评估的指标。

本文探索性地应用BP神经网络评估科创板企业价值，但是该模型也存在以下不足：一是指标问题：由于科创板企业信息披露不完善，所以很多因素没有考虑，如风险因素等。二是样本问题：本文样本数据有191条，数据规模较小，且这191家公司经营范围不同，这都会影响模型学习的效果。

【参考文献】

［1］林妍.我国科创板上市公司市场价值评估分析［J］.会计之友，2020（23）：140-143.

［2］宋丽平，李萌，于书洋.基于GRNN神经网络的科技型企业价值评估方法研究［J］.科技与管理，2020，22（2）：91-97.

［3］ LI XIMEI.Research on value assessment of scientific and technological enterprises based on BP neural network［J］.IOP Conference Series：Materials Science and Engine-ering，2020，750.

［4］张陆洋，钱瑞梅.关于科创企业估值难点的思考［J］.安徽师范大学学报（人文社会科学版），2019，47（4）：104-110.

［5］胡沛.企业财务指标对科创板上市公司成长性影响的实证分析［D］.哈尔滨：哈尔滨工业大学硕士学位论文，2020.

［6］贾玉辉，宁金辉.IPO热潮下科创板拟上市企业绩效评价研究［J］.经济体制改革，2021（2）：102-108.

［7］林新奇，赵国龙.基于DEA方法的我国科创板企业创新绩效研究［J］.科技管理研究，2021，41（1）：54-61.

［8］左庆乐，刘杰.高新技术企业价值评估的基本问题探析［J］.中国资产评估，2001（6）：20-23，4-5.

［9］郭建峰，王丹，樊云，等.互联网企业价值评估体系研究——基于实物期权模型的分析［J］.价格理论与实践，2017（7）：153-156.

［10］汤姆·科普兰，蒂姆·科勒，杰克·默林.价值评估：公司价值的衡量与管理［M］.3版，北京：电子工业出版社，2002.

［11］郭蓬元，韩秀艳.基于实物期权的高科技创业公司价值测度研究［J］.科学管理研究，2021，39（1）：116-122.

［12］谢喻江.基于EVA的成长期高新技术企业价值评估［J］.财会通讯，2017（5）：7-11.

［13］李素英，王贝贝.基于级数突变法的科技型中小企业价值评估研究［J］.经济研究参考，2017（34）：101-108.

［14］付扬扬，仇晓洁.基于BP神经网络的创业板上市公司价值评估［J］.中国资产评估，2019（2）：35-40.

［15］朱敏.基于BP神经网络技术的智能财务研究［J］.会计之友，2021（18）：38-42.