基于车桥耦合等截面连续梁桥单损伤识别研究

张智越, 李雪峰, 王成玉

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.合肥工业大学设计院(集团)有限公司,安徽 合肥 230051)

国内研究者对桥梁结构损伤识别早期存在的问题给予了大量关注,并对结构的损伤检测进行了诸多的初步试验,以Los Alamos国家实验室和ASCE健康监测委员会更具有代表意义[1]。文献[2-3]列出了假设损伤的结构整体刚度会微妙地发生改变,运用车辆通过桥梁时对桥梁结构振动产生的影响,来识别结构损伤的方法,但对于桥梁在局部存在的损伤,又一时不能识别变化的系统随时间的损伤。因此,随着损伤识别方法的进一步发展,有研究者提出了一种时域损伤识别方法,文献[4]基于研究的智能结构,借助时域动力响应成功实现了损伤识别;文献[5]以时域动力响应为基础,针对结构各单元动力特性参数的变化规律进行了理论分析,发现可以识别结构的单元损伤范围,较大程度发展了结构损伤识别方法,但在实际生活中较难应用。研究者考虑车辆参数发生改变在结构损伤识别中的影响,也进行了诸多的研究工作。文献[6]以简支梁桥为研究对象,在考虑到路面不平整因素对简支梁桥振动响应影响的基础上,对车辆参数的变化在桥梁的振动响应中存在的影响展开了理论研究;文献[7]基于车辆行驶过桥梁时,车辆引起桥梁产生的振动响应,利用灵敏度分析的方法,实现对桥梁的损伤识别;文献[8]将车辆简化为车辆模型,求解结构单元刚度的偏导,以建立灵敏度矩阵,结构单元刚度的计算以及对结构损伤的识别都是采用迭代方法;文献[9]以移动荷载作用下简支梁桥结构为研究对象,利用小波多变率的方法识别结构的单处或多处裂纹损伤存在的位置;文献[10]以简支梁桥为研究对象,在车桥耦合动力响应的基础上,利用经验模态分解(empirical mode decomposition,EMD)以及Hilbert谱分析的方法,实现对桥梁结构的损伤识别。

随着研究的不断深入,基于车桥耦合振动的桥梁损伤识别方法,有灵敏度分析方法和基于耦合振动信号后处理的识别方法,包括小波分析法、Hilbert-Huang变换法等。还有基于人工智能的损伤识别方法,包括神经网络分析法、遗传算法等。上述大多数的损伤识别研究都是针对简支梁桥或都需要将桥梁或车辆的振动响应信号进行处理,连续梁桥由于其支座处的负弯矩可以抵抗跨中正弯矩,大大提高了结构的跨度,成为众多桥梁采用的结构形式。

目前关于不需要进行信号处理的连续梁桥损伤识别的研究较少,针对多跨等截面连续梁桥的特点,本文展开了损伤识别研究。

1 车桥耦合振动方程建立

1.1 车辆振动方程

建立1/4车辆模型时,本文作如下假设[11]:

(1) 车辆分为车体及悬架系统2个部分,假设它们之间的连接为弹簧与阻尼器。

(2) 在不计算车辆自身形变的情况下,把车辆假设为一个绝对刚体结构。

(3) 弹簧处于理想状态下,不会出现弹簧故障。

(4) 保证车辆以匀速行驶通过桥梁,并始终与桥面紧密接触。

1/4车辆模型如图1所示。

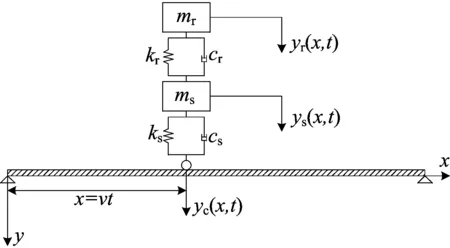
图1 1/4车辆模型

图1中:mr为车体的质量;yr(x,t)为车体本身的竖向位移;kr、cr分别为连接车体与悬架系统之间的弹簧刚度、阻尼系数;ms为车辆悬架和车轮的总质量;ys(x,t)为车辆悬架以及车轮系统的竖向位移;ks、cs分别为车辆悬架与车轮系统的弹簧刚度、阻尼系数;yc(x,t)为桥梁与车辆轮胎接触点处的竖向位移。

根据达朗贝尔原理,通过对车体及悬架系统的深入分析,分别得到了两者的振动响应微分平衡方程。

对于车体,有

(1)

对于悬架与轮胎系统,有

(2)

两者转换为矩阵形式后的方程为:

(3)

其中

1.2 桥梁模型的建立

连续梁桥的受力相对复杂,为了简化计算,本文将待计算的桥梁截面简化为等面积的矩形截面,把钢筋等效为混凝土,再以欧拉伯努利梁的基本理论为基础,推导车桥的振动平衡方程。考虑梁体承受均布竖向外力f(x,t)和轴向力p,受力示意图如图2所示。

图2 等截面连续梁受力示意图

基于文献[12]对连续梁单元体进行受力分析的理论,取dx位于桥轴线x位置的单元视为对象,该单元体的受力如图3所示。

图3 梁单元体的计算模型

通过图3中的单元体竖直力平衡和o点力矩平衡Mo=0得到:

(4)

(5)

假设荷载沿x、y方向的位移为u(x,t)、v(x,t),建立欧拉伯努利梁理论[13-14]方程,即

(6)

v(x,z,t)=v0(x,t)

(7)

其中:u0(x,t)、v0(x,t)分别为中性轴上任意一点的轴向位移和横向位移;z为梁上任意一点与中性轴间的距离;t为时间。

根据Von-Karman的基于大横向位移、中等转动、小应变假设的非线性应变-位移的关系[15],并忽略轴向位移u0(x,t)对梁截面的影响,可以得到梁的应变与位移间的几何关系,即

(8)

(9)

根据Kelvin-Voigt模型[15]应力-应变本构关系可以得到:

(10)

其中:σx为应力;η为桥梁材料的阻尼。

根据弯矩与应力、轴力与应力之间的关系可以得到:

(11)

(12)

其中,b、h分别为梁截面的宽度、高度。

将(10)式分别带入(11)式、(12)式可得:

(13)

(14)

其中,p为预应力效应引起的轴向力。

将(13)式、(14)式分别带入(4)式、(5)式,可得:

(15)

在建立振动平衡方程时,考虑到桥面不平整因素对桥梁振动响应的影响,对桥面不平整函数r(x)进行模拟,可以得到车辆驶过桥梁时对桥梁结构的作用力Q(t)为:

Q(t)=(mr+ms)g-ks[ys-yc-r(x)]-

(16)

f(x,t)=-δ(x-vt)Q(t)

(17)

其中,δ为Dirac函数。

根据振型分解法可用于求解非线性振动方程(15)式,设φ(x)i、λ(t)i分别为连续梁的第i阶模态函数与模态坐标[16],假设取定桥梁设计总长度为L,将yc分解式代入(15)式,同时在方程两边乘以φ(x)n,然后将方程在整个连续梁桥进行积分,并运用伽辽金法[12]对其进行简化,可以得到:

(mr+ms)gφ(x)n

(18)

对于等截面连续梁,相应的线性第n阶振型为:

φn(x)=ansin(αnx)+bncos(αnx)+

cnsinh(αnx)+dncosh(αnx)

(19)

为了简化计算,记

(20)

(21)

(22)

(23)

则(18)式可简化为:

(mr+ms)gφ(x)n

(24)

(24)式为计算得到的连续梁桥自身相应频率每阶振型的非线性振动方程。

1.3 车桥耦合方程的建立及求解

根据建立的移动车辆模型与桥梁非线性模型,并结合车辆与桥梁的振动,能够推导出相应的车桥耦合方程。

车桥耦合方程为:

(25)

其中:M(t)为广义质量矩阵;C(t)、K(t)分别为广义阻尼矩阵及广义刚度矩阵;S(t)、D(t)分别为非线性因素影响的相关矩阵;F(t)为外力矢量;X为广义位移矢量。

(26)

(27)

(28)

(29)

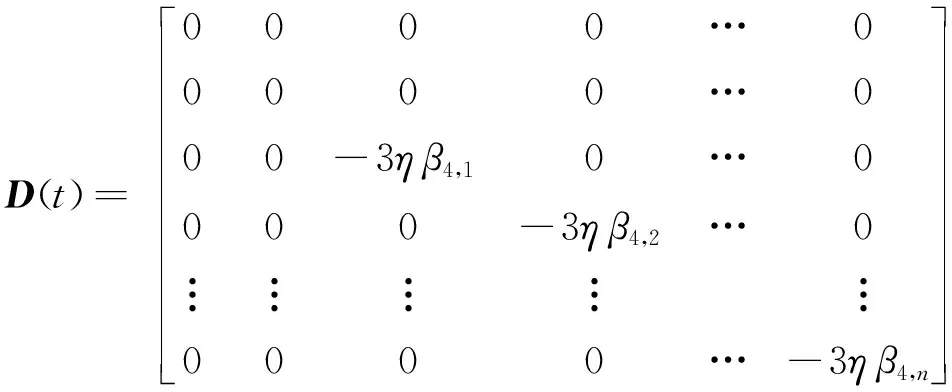
(30)

(31)

(32)

假设车辆在桥梁上以匀速行驶,则x=vt,联立方程φmn=φ(vt)mφ(vt)n,本文选用适用于计算的Newmark-β法对车桥耦合方程进行数值求解,成功得出车桥耦合系统的振动响应。

损伤识别流程及优点如下:① 首先通过比较损伤前后每跨跨中竖向位移曲线判断出损伤跨,与无损状态相比出现增大现象的为损伤跨;② 然后根据损伤跨的跨中响应与无损时的曲线差值判断出损伤位置,偏差最大处出现的位置即可作为损伤识别指标,进行等截面连续梁桥单损伤识别研究。

本文以车桥耦合振动系统为研究对象,根据连续梁桥每一跨直观的跨中竖向位移响应变化,以识别桥梁结构的损伤,是对车桥耦合振动原始信号的研究,无须再进行信号处理,提高了实际应用中的可操作性。

2 连续梁桥损伤识别研究

本文主要识别连续梁桥发生裂缝损伤时的位置,当桥梁存在裂缝时,损伤位置的质量几乎没有变化,但是,损伤位置的刚度将下降。假设连续梁桥存在裂缝损伤时,损伤位置的质量没有变化,通过降低单元刚度的方法模拟桥梁的损伤。分别计算出损伤跨桥梁的跨中竖向位移,并与相应桥梁设计无损伤状态时进行比较,以识别连续梁桥的损伤情况。

以(20+25+20) m的等截面连续梁桥为例,对其进行研究,桥梁上部结构采用C50混凝土,混凝土密度ρ=2.5×103kg/m3,弹性模量E=3.45×1010Pa,惯性矩I=1.280 1 m4,阻尼比δ=0.02。

车辆模型参数为:mr=3.85×104kg,kr=5.07×106N/m,cr=3.82×105kg/s,ms=8.66×103kg,ks=8.56×106N/m,cs=1.96×105kg/s。

2.1 跨中损伤

本文分别假定裂缝损伤发生在连续梁桥每跨跨中位置处,刚度折减30%、50%,车辆以36 km/h匀速通过桥梁,分别计算连续梁桥第1跨、第2跨与第3跨跨中竖向位移,并与相应桥梁设计无损伤状态时的位移响应进行比较,结果如图4～图6所示。

图4 第1跨跨中损伤时各跨跨中竖向位移响应对比

由图4可知,当连续梁桥第1跨跨中存在损伤时,其跨中竖向位移大于无损伤时位移响应,当车辆驶至第2跨和第3跨跨中时,桥梁损伤大小由无损逐渐增大,相应的跨中竖向位移响应逐渐减小,且比相应桥梁无损伤状态时要小得多。当车辆行驶至桥梁的8.7 m位置时,损伤位置的位移响应增加值最大,桥梁损伤大小由无损逐渐增大,第1跨跨中竖向位移响应增加值为0.029、0.035 mm。因此,当车辆行驶至损伤位置附近时,跨中竖向位移响应将增加,能够判别出损伤处的位置区间;车辆行驶至每跨跨中时,相应跨中的位移与无损伤状态时之间的偏差大小能够判别出该跨的相对损伤程度。

从图5可以看出,连续梁桥第2跨跨中存在损伤时,第1跨和第3跨跨中位移响应曲线基本上与无损伤状态时一致,且偏差非常小。当第2跨跨中损伤大小为30%、50%时,车辆分别行驶至桥梁的33.2、33.7 m位置处,第2跨跨中竖向位移逐渐增加,且比相应无损伤状态时增加值要大得多,分别为0.064、0.132 mm。因此能够判别出连续梁桥第2跨跨中的损伤大小和相对损伤程度。

图5 第2跨跨中损伤时各跨跨中竖向位移响应对比

由图6可知,当车辆行驶至连续梁桥第3跨跨中时,损伤大小由无损逐渐增大,第3跨跨中的竖向位移响应增大,且逐渐大于无损伤状态时的竖向位移响应。当车辆行驶至桥梁55.8 m位置时,第3跨跨中损伤大小分别为30%、50%时,竖向位移响应增加值最大,分别为0.058、0.103 mm。因此能够判别出第3跨跨中的损伤大小和相对损伤程度。

图6 第3跨跨中损伤时各跨跨中竖向位移响应对比

2.2 非跨中处损伤

假设连续梁桥损伤发生在第1跨的3/5位置、第2跨的1/5位置、第2跨的2/3位置及第3跨的4/5位置处,刚度折减依次为30%、50%,车辆以36 km/h匀速通过桥梁,计算出每跨的跨中竖向位移,并与相应的桥梁设计无损伤状态时竖向位移响应进行比较,如图7～图10所示。

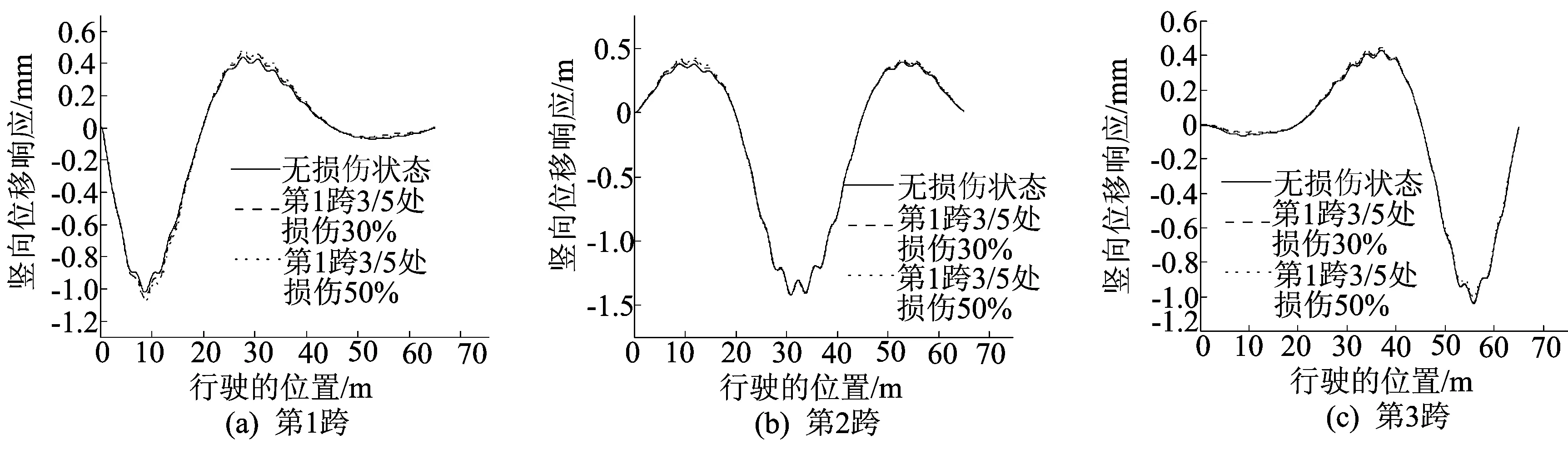
图7 第1跨3/5处损伤时各跨跨中竖向位移响应对比

由图7可知,第1跨的3/5位置处发生损伤时,在连续梁桥的第1跨,损伤大小由无损逐渐增大,在第1跨跨中的竖向位移响应与无损伤状态之间存在较大的偏差范围;当车辆行驶到第2跨跨中时,桥梁无损伤状态时的竖向位移与损伤桥梁的第2跨跨中竖向位移响应基本一致,偏差非常小;车辆行驶至第3跨跨中时,损伤大小由无损逐渐增大,桥梁无损伤状态时的位移响应比第3跨跨中的位移大。

当车辆行驶至桥梁11.6 m位置时,损伤大小由无损逐渐增大,无损伤状态时的竖向位移比第1跨跨中增加值最小,分别为0.040、0.068 mm,且在桥梁第1跨3/5位置发生损伤时,偏差最大,因此,能够判别桥梁损伤的位置区间,还可以根据偏差大小判别出相对损伤程度。

由图8可知,第2跨1/5位置处发生损伤时,车辆行驶至第1跨、第3跨时,随着损伤大小由无损逐渐增大到30%、50%时,第1跨跨中峰值位移分别为1.020、-0.999、0.950 mm,第2跨跨中峰值位移分别为0.380、0.374、0.362 mm,研究结果表明,桥梁无损伤状态时竖向位移比第2跨跨中位移大。在车辆行驶至第2跨时,单元处于临界位置,此位置之前,无损伤状态时的竖向位移与第1跨以及第2跨跨中竖向位移基本一致,偏差非常小;此位置之后,损伤大小由无损逐渐增大,桥梁无损伤状态时竖向位移比第1跨以及第2跨跨中竖向位移大,由无损增加到损伤程度为30%、50%时,第1跨跨中峰值位移分别为0.439、0.444、0.439 mm,第2跨跨中峰值位移分别为-1.22、-1.20、-1.181 mm,偏差较明显。因此,能够根据临界位置处前、后的变化规律,判别出桥梁的损伤位置在第2跨临界处,通过偏差大小能够判别出该跨的相对损伤大小。与以往的损伤识别规律对比,上述现象具有特殊性。然后假设除了桥梁第2跨跨中位置之外,其他位置都发生损伤,并且在第2跨2/3处发生损伤,由图9可知,该规律与第2跨1/5位置发生损伤时的规律基本一致。

图8 第2跨1/5处损伤时各跨跨中竖向位移响应对比

图9 第2跨2/3处损伤时各跨跨中竖向位移响应对比

由图10可知:第3跨的4/5位置处发生损伤时,当车辆行驶至第1跨跨中时,桥梁无损伤状态时的竖向位移比第1跨跨中位移大,但偏差较小;当车辆行驶至第2跨时,桥梁无损伤状态时的位移与第2跨跨中位移基本一致,偏差非常小;车辆行驶至第3跨时,桥梁无损伤状态时的位移与第3跨跨中竖向位移之间的偏差程度大,但偏差较小;当车辆分别行驶至桥梁61.5、61.4 m处,第3跨4/5位置处损伤大小分别为30%、50%时,第3跨跨中竖向位移增大值最大,分别为0.015、0.040 mm,此时车辆正好行驶至第3跨4/5处。由此也能够判别损伤的位置区间,还可以根据偏差程度判别相对损伤程度。

图10 第3跨4/5处损伤时各跨跨中竖向位移响应对比

2.3 信噪比对连续梁桥损伤识别的影响

在桥梁实际运营中,噪声不可避免,车桥耦合振动得到的跨中位移响应应考虑存在噪声的影响,对图5b的第2跨跨中位移响应添加不同信噪比下的高斯白噪声,以分析噪声对连续梁桥损伤识别的影响。信噪比计算公式为:

(33)

其中:y(n)为纯信号序列;z(n)为高斯白噪声序列;N为项数;RSNR为信噪比。

信噪比取40、50 dB,刚度折减30%,计算得到桥梁无损伤和第2跨跨中损伤30%的跨中竖向位移响应,如图11所示。

图11 信噪比为40、50 dB时桥梁无损伤与受损伤跨中竖向位移对比

由图11可知,第2跨跨中位置发生30%损伤时,当信噪比为40 dB时,曲线存在细节波动性,桥梁无损状态和受损伤跨中位移出现差异,当车辆行驶到连续梁桥跨中时偏差最为明显,两者峰值相差0.069 mm,比无噪声时大0.180 0 mm,说明在一定情况下噪声可以对位移响应产生影响。当信噪比进一步提高为50 dB时,曲线逐渐逼近图5b,细节波动性明显降低,无损伤和受损伤桥梁跨中位移差异更加明显,两者峰值相差0.05 mm,损伤识别效果比无噪声时低0.000 9 mm,可完全可以忽略。因此,一定条件下噪声的存在不会影响本文损伤识别的效果,并随着信噪比的增大,位移响应曲线逐渐逼近于无噪声曲线,损伤识别效果较好。

3 结 论

本文以车桥耦合系统为基础,选取1/4车辆模型,以三跨等截面连续梁桥为例,求解车桥耦合振动方程,得到桥梁特殊关键位置的振动响应,对桥梁单处裂缝进行损伤识别,得到如下结论:

(1) 通过刚度折减能够模拟桥梁的裂缝损伤,当车辆在桥梁上匀速行驶,通过求解桥梁关键位置的振动响应,并与桥梁无损伤状态时的振动响应进行对比,能够进行桥梁的裂缝损伤识别。

(2) 当裂缝出现在每跨跨中位置时,车辆行驶至损伤位置时,会造成该跨跨中竖向位移响应增加,能够判别出损伤桥梁的位置范围,且随损伤大小的增加,竖向振动位移响应偏差越大,能够采用位移响应的偏差大小判别相对损伤程度。

(3) 当裂缝出现在第1跨及第3跨非跨中位置时,车辆行驶至损伤位置处,造成该跨跨中响应增大,且偏差程度的范围也较大,其中靠近损伤单元位置的偏差较大;当裂缝出现在第2跨非跨中处时,其识别的现象具有特殊性,损伤单元处于临界位置,此位置之前与之后,第2跨跨中位移响应表现出非一致的规律。但均能够判别出桥梁损伤的位置区间范围和相对损伤程度。

综上所述,基于车桥耦合振动得到的位移响应信噪比较大,将桥梁的车致振动响应与无损伤状态时桥梁的车桥耦合振动响应比较进行裂缝损伤识别,在理论上是行之有效的。