在初中数学解题中有效应用数形结合

李明超

数形结合是一种常见的解题方式，它的应用不仅可以打开学生的思维，还能提升学生的解题效率。本文以初中数学为研究对象，简述了数形结合思想，分析了采用数形结合思想开展教学的优势，并以案例的方式对其在解题中的应用进行深入的研究。

新课程理念指导下的数学教学不单注重学生知识学习，更加强培养学生的数学思维。针对这一现实情况，教师必须改变陈旧的教学模式，在开展基础教学的同时，加强对学生数学思维的培养，让学生在主动参与中获取知识、提升能力。教师应用数形结合这一教学方法，可以帮助学生建立起系统思维模型，提升学习效率。因此加强数形结合思想在数学解题中应用的研究非常重要。

一、数形结合思想概述

数形结合即数与形的对应，教学中教师通过数与形间的转化可以让学生轻松地解答问题。随着教学改革的发展，教师的教学理念也在发生转变，从知识教学转向学习思想的培育。数形结合模式在解题中的应用，降低了学生的数学学习难度，深化了学生对知识的理解。教师将数形结合思想应用于数学解题中，不仅解决了解题的难点，而且提升了学生的解题效率。教学改革的持续发展，使各个阶段的教育获得了发展，在为国家培养创新人才方面发挥着重要的作用。但人才的培养是一个长期的过程，特别是要打好基础。数学作为初中阶段的一门基础学科，因抽象性、逻辑性强的特点加大了学生的学习难度。数学教学不仅要注重学生的知识掌握度，更要关注学生数学思维能力的发展，由此数形结合的思想就进入了大家的视野，并在课堂教学中得到了广泛的应用。

二、初中数学教学中应用数形结合法的优势

（一）应用范围广，适用于不同类型的数学知识

以往的初中数学教学形式单一，教师往往采取“灌输”的方式，力图通过详细地向学生分析数学知识来达到让学生理解的目的。在这一过程中，学生机械地学习，让数学学习失去原本的魅力。长此下去，学生在数学课上就会消极，采用单一的学习方法，固化了数学思维。而数形结合是数学思想方法的一种，主要通过数和形的相互转换来解决实际问题，因此这一方法得到了广泛应用，而且根据不同的知识点可以展现出不同的效果，以此优化数学课堂。

（二）涉及思想方法，拓宽学生的数学思维

数形结合是数学思想的一种，它强调灵活解读和应用，是数学知识内化的一种表现。加强数形结合思想在初中数学中的应用，可以帮助学生把握知识的内在关联，通过长期的训练可以促进学生数学思维的发展。将数形结合思想应用于不同问题的解答中，可以让学生认识到思想方法的重要性，通过汲取数学思想和方法完善自己的学习体系。

（三）锻炼解题技巧，提升学生的解题效率

数形结合不单是解决问题的有效方法，更是一种思维的体现。学生通过数形结合思想的学习可以解决数学难点，可以达到举一反三的效果，用它来解决更多的问题，也可以促使学生形成一种思维模式，在长期的坚持和锻炼中掌握解题技巧，这对学生日后的成长与发展有着现实意义。

三、初中数学教学现状

刚进入初中的学生，因其思维、学习方法还停留在小学阶段，所以在学习中会出现各种问题。升入初中后学习的难度会逐渐加大，这不仅影响着学生的学习效果，而且会导致学生降低学习兴趣，从而让学生无法全身心地进入数学课堂中。教师在教学中应用数形结合思想，帮助学生更轻松地掌握知识，提高课堂质量。但受到传统教学形式的影响，当下的课堂教学中还存在诸多问题。

（一）教师教学方法单一

在以往的数学课堂中，教师会采取“灌输”的模式开展，并试图通过“题海”战术让学生掌握某个知识点，这不仅加大了学生的压力，而且限制了学生的发展。针对这一现实情况，教师只有加强创新和优化教学方法，才能为数学课堂注入更多的趣味元素，才能在这种思想方法的引导下习得知识、解决问题，并促使学生更好地学习。

（二）数学难度大，降低了学生的学习热情

从小学到初中，数学学习的难度明显加大，这就导致部分学生在课堂的收获甚微，从而打击了学生的信心，降低了学习热情。教师应用数形结合思想则可以轻松地解决这一问题，通过数和形的转变可引发学生深入思考，以此来降低学习难度，让学生有效理解知识，为其数学综合思维能力的发展打下坚实的基础。

（三）教师忽视数形结合思想

数形结合思想在学生数学学习中发挥着重要的作用，特别是在初中阶段，贯穿着整个过程，对其的应用影响着学生解答问题的速度与能力。但在以往的教学中很多教师都忽视了对其的应用，忽视了在解题中渗透数形结合思想，认为教学的重点在于解决实际问题。其实不然，应用数形结合思想是学生必备的一项能力，特别是初中生正处在形象思维向抽象思维过渡的阶段，加强数形结合思想的学习非常重要。

四、数形结合在初中数学解题中的有效应用分析

在数学问题的解决中学生只有灵活应用知识，并通过有效的训练才能获得更多的答题技巧，也才能进一步提升自身解决实际问题的能力。而在这一问题的解决过程中，加强数形结合思想方法的应用可以将题目中的条件直观地展现出来，便于学生理解其中的含义，并最终提升学生解决问题的能力。

（一）巧用数形结合思想解决正数和负数问题

刚进入七年级的学生，思维还处在形象阶段，面对难度更大、抽象性更强的数学知识点，只有在教师的引导下才能完成，才能进一步提升其数学思维能力。例如，在正数和负数的概念的教学中，教师便可以采用数轴的方法对学生进行引导，首先在黑板上画出一个数轴，中点表示为0，左边为负数，右边为正数，然后再创设“气温低于0度和气溫高于0度”的生活情境，让学生将-5度、-10度和+5度、+10度刻画在数轴上，以帮助学生把握正数和负数的概念。这一简单应用，给了学生启发，而且在接下来的重点学习中，学生也可以举一反三，结合这一思想方法解答问题。

（二）巧用数形结合思想解决函数问题

函数是中学阶段的学习重点，但由于函数的抽象性和逻辑性，学生在函数学习中出现了各种问题。所以在学习中，教师可以指导学生采取数形结合的方法对一元一次方程、一元二次方程以及二元一次方程进行归纳，将其特点展现出来，方便学生理解和接受，进而在解答方程问题时能够游刃有余。为了深化学生的学习，教师可以设置问题“一次函数与二次函数存在哪些异同点”，此时学生就会想到利用数形结合思想进行解答，首先在纸上画出一次函数y=kx+b和二次函数y=ax2+bx+c（且a≠0）的图象，学生便可以清晰看到两者的区别。然后再根据对不同函数图象的分析，让学生认识到了一次函数和二次函数各元素的作用，为学生后续根据各元素的作用解答问题提供了特定的条件。

（三）巧用数形结合思想解答几何问题

初中数学几何知识的范围很广，有三角形、平行四边形、圆形和圆柱体知识等，为了帮助学生探究其中的本质，教师可以应用数形结合思想。比如，在“勾股定理”这节知识的教学中，教师可以为学生展示生活类的问题，让学生根据所学的知识和以往的经验进行解答，然后利用数形结合思想将题目中的条件转化为直角三角形，再利用勾股定理知识解答现实问题。

例如，“老师要求同学们测量学校旗杆的高度，小明发现旗杆顶端的绳子垂到地面后还多出1 m，当他把绳子的下端拉开5 m后，发现绳子下端刚好接触地面，你能帮助小明求出旗杆的高度吗？”根据题目的条件，学生可以画出相应的图形，而后会发现旗杆和地面两者的结合正好是直角三角形的两条直角边，然后会联想到所学的勾股定理知识，再根据勾股定理的概念和公式，自然可以列出勾股定理的方程。求解：设绳子的长度AB为x m，则旗杆的高度AC为（x-1） m，在直角三角形ABC中，得出AC2+BC2=AB2，也就是（x-1）2+52=x2，由此可以得到x=13，则x-1=12，所以旗杆的高度为12 m。

又如，在圆的有关知识的学习中，为了提升学生对圆的认识，教师可以指导学生利用数形结合的思想，分析圆和圆的位置关系，而后加深学生的印象。最后教师再设计相应的习题，鼓励学生解答，不但丰富了学生的知识储备，而且提升了学生解答数学问题的效率。

（四）巧用数形结合思想解决数学不等式问题

学生若采取传统的方法解答不等式，需要求出每一个不等式的解集，在数轴上画出来，然后找到不等式的公共部分便可以得到不等式组的解集。因此，在这部分知识点的教学中，教师可以从简单的题目入手，在学生熟悉数形结合思想方法后，再加大学习难度，为学生多设计几个题目，最后邀请学生将自己解题的方法和过程展现出来。有的学生采取了直接计算的方法，有的学生用数轴表示，这是学生数学思维和数学能力的充分体现。为了开阔学生的思维，教师可以将班内学生划分为不同的小组，指导学生以小组的方式求出如下的二元一次方程组：x+2y=2m-5x-2y=3-4m，若x为正数，y为负数，求m的取值范围。本道题目和以往的二元一次方程求解不同，因为题目中有未知数m，但教师可以指导学生结合数形结合的方法进行思考。在小组讨论中，深得数形结合思想方法的学生会提出采取数轴的方法解答，然后根据题目中给出的条件，得到m的取值范围。经过长期的训练，学生不仅掌握了不等式的解答方法，而且为日后利用这一数学思想方法解答更高难度的问题奠定了基础。

（五）巧用数形结合思想解决线性规划问题

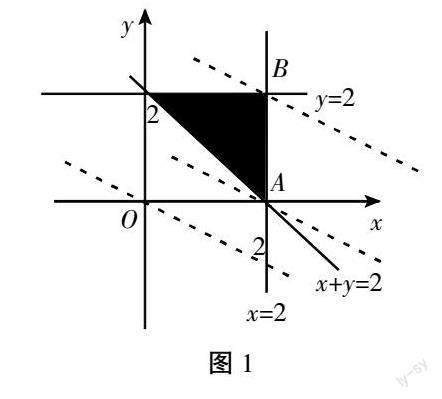
数形结合方法是解决线性规划问题的有效方法，在此类问题的解答中，根据题目给出的条件作图，然后通过分析找出正确的区域，最后进行作答。例如，在解决如下线性规划问题“若x、y、z满足约束条件x≤2，y≤2，x+y≥2，则z=x+2y的取值范围是多少？”时，就可以引导学生采用画图的方式画出x与y的数轴（如图1），然后根据题目中给出的条件进行绘制，再通过观察与分析就可以轻松得到问题的答案。

由上可见，在线性规划问题的解答中，利用数形结合法解答问题非常重要，但需要学生画出正确的区域，才能根据题目条件得到正确的答案。因此在此类问题的解答中，学生必须牢记数形结合方法，如此才能提升学生答题的速度和准确率。

综上所述，初中生只有灵活应用知识，在问题的解答中才能更加游刃有余。同样，教师引导学生利用数形结合思想解决问题，可以使复杂问题简单化，可以将抽象的数学语言以直观的图形展示出来，可以帮助学生把握住数学问题的本质。而且大量的教學实践研究显示：数形结合思想的应用，可以促进学生的全面提升与发展，在当下的数学教学中发挥着重要的作用。数形结合是一种先进的数学思想，教师对其的应用创新了教学模式，因此在日后的教育教学中，教师要将数形结合的思想融入数学问题的解答中，通过创新模式、细化目标，吸引学生主动参与，同时激活学生的数学思维，将学生的内在潜力挖掘到位，为学生数学核心素养的形成奠定坚实的基础。

参考文献：

[1]金明.映“数”“形”花别样红：数形结合思想在初中数学解题中的应用[J].新课程（中学版），2014（1）：218-219.

[2]马威.数形结合思想在初中数学解题中的应用[J].中学生数理化（教与学），2021（35）：71-73.

[3]胡丽琴.数形结合思想在中学数学解题中的应用[J].中华少年（研究青少年教育），2012（7）：315-316.

[4]王静.浅析数形结合思想在初中数学解题中的应用[J].世纪之星（初中版），2022（11）：172-174.

（作者单位：贵州省兴仁市波阳镇田湾中学）

编辑：张俐丽