集值优化问题E-Henig有效解的稳定性
2023-07-04胡瑞婷彭家玉丁若文
曾 静,胡瑞婷,彭家玉,丁若文
重庆工商大学 数学与统计学院,重庆 400067
1 引 言
集值优化问题包含了向量优化、数值优化等多种优化问题,具有丰富的实际背景,是优化领域的研究热点之一。有关这一问题的研究涉及变分分析、数理经济、博弈论等多个学科分支,它与学科间的密切联系极大程度上拓宽了集值优化问题理论研究和实际应用的范围。近年来,学者们已取得了一系列的研究成果[1-6]。2012年,Gutiérrez等[7]基于改善集给出了E-有效解的定义,不仅对数值优化问题的解进行了进一步推广,还把向量优化问题的几个解(有效解、近似有效解、弱有效解、近似弱有效解)进行了统一;2015年,赵克全和杨新民[8]首次定义了E-Benson真有效解,它是经典真有效解和近似真有效解概念的合理推广; 2017年,林佩静[3]在研究中给出E-Henig真有效点的定义、等价刻画、解的特征等。目前关于Henig有效解的最优性条件[9]、连通性[10-11]、对偶性[12-13]等方面的研究已经比较成熟,但鲜有文献研究集值优化问题改善集下Henig有效解的稳定性。由上述文献可以看出:以往学者聚焦于集值优化问题Henig有效解的存在性、最优性、对偶性等方面的研究,大大丰富了集值优化问题有效解性质的研究,进一步推动了优化问题的发展。而改善集下的Henig有效解统一了Henig有效解和近似Henig有效解,其稳定性分析是数值计算中必不可少的环节,因此研究集值优化问题E-Henig有效解的稳定性具有重要的理论意义和实用价值。但基于改善集下的集值优化问题E-Henig有效解的研究还少之又少,文献[3]虽然对其进行了研究,但其主要研究改善集下集值优化问题E-Henig有效解的存在性、鞍点、对偶性。本文致力于改善集下集值优化问题E-Henig有效解的稳定性研究。值得一提的是,2004年,Lucchetti和Miglierina[14]在目标映射和约束条件均扰动的情形下研究了凸向量优化问题有效点集和解集的稳定性;2014年,李小兵等[15]在扰动问题序列Painlevé-Kuratowski收敛到目标优化问题时,建立了严格真拟C-凸向量优化问题Henig有效点集和解集的稳定性。随后几年,李小兵等[16]讨论了当近似问题的数据Painlevé-Kuratowski收敛到原问题的数据时,拟凸集值优化问题3种解(有效解、弱有效解、Henig有效解)的点集和解集的稳定性。文献[14,15]为向量优化问题有效解的稳定性研究做出了贡献,本文拟借助文献[16]的研究方法,将文献[14,15]的结果进一步推广至集值优化问题中。因此,本文拟在目标映射和约束条件都扰动的情况下,获得严格真拟C-凸集值优化问题E-Henig有效点集和解集的稳定性结果,推广文献[14-16]中的相关结果,为集值优化问题E-Henig有效解的实际数值计算分析提供重要的稳定性理论分析依据。
2 预备知识
本节主要介绍集值映射的一些相关概念和性质。
设C为Rl中非空的集合,若x∈C,λ≥0能推出λx∈C,则称集合C为锥;若C≠{0}且C≠Rl,则称C为真锥;若C∩(-C)={0},则称C为尖锥;若cl(C)是尖锥,则称C为锐锥;若C既是尖锥,又是锐锥,则称C为尖锐锥。设有非空集合S⊂Rm,称集合{λs|λ≥0,s∈S}是由集合S生成的锥,记为cone(S);定义∂S是非空集合S的边界;设C为Rl中内部非空的尖闭凸锥,Rl中C诱导的偏序如下:y≤Cx⟺x-y∈C,y 设F:S→2Rl是从S到Rl的集值映射,考虑如下集值优化问题: (S,F):minx∈SF(x) 首先回顾集值优化问题(S,F)的几种解的定义、改善集的定义、改善集下解的定义以及相关性质。从现在起,总假设非空集合S⊂Rm,F(S)=∪x∈SF(x),C为Rl中内部非空的尖闭凸锥。 定义1[11,15]设y∈F(S),ε∈intC,若存在满足C{0}⊂intC1的内部非空尖闭凸锥C1,使得(F(S)-{y}+ε)∩(-C1{0})=∅,则称点y为集合F(S)的ε-近似Henig有效点; 记集合F(S)中所有ε-近似Henig有效点构成的集合为ε-HMinF(S);若x0∈S,存在y0∈F(x0),使得y0∈ε-HMinF(S),则称点x0为集值优化问题(S,F)的近似Henig有效解;记集值优化问题(S,F)所有近似Henig有效解构成的集合为ε-HEff(S,F)。 定义2[15]设y∈F(S),若存在满足C{0} ⊂intC1的内部非空尖闭凸锥C1,使得(F(S)-{y})∩(-C1{0})=∅,则称点y为集合F(S)的Henig有效点;记集合F(S)所有Henig有效点构成的集合为HMinF(S);若x0∈S,存在y0∈F(x0),使得y0∈HMinF(S),则称点x0为集值优化问题(S,F)的Henig有效解;记集值优化问题(S,F)所有Henig有效解构成的集合为HEff(S,F)。 定义3[8]设E为Rl中的一个非空子集,C为Rl中内部非空尖闭凸锥,若满足0∉E且E+C=E,则称E为关于C的一个改善集,记Rl中关于C的改善集全体为ξY。 定义4[8]设E∈ξY,y∈F(S),若点y满足(F(S)-{y})∩(-intE)=∅,则称点y为集合F(S)的E-弱有效点;记F(S)所有E-弱有效点构成的集合为EWMinF(S);若x0∈S,存在y0∈F(x0),使得y0∈EWMinF(x0),则称点x0为集值优化问题(S,F)的E-弱有效解;记集值优化问题(S,F)所有E-弱有效解构成的集合为EWEff(S,F)。 定义5[8]设E∈ξY,y∈F(S),若点y满足(F(S)-{y})∩(-E-C{0})=∅,则称点y为集合F(S)的E-有效点;记F(S)所有E-有效点构成的集合为EMin (S); 若x0∈S,存在y0∈F(x0),使得y0∈EMinF(x0),则称点x0为集值优化问题(S,F)的E-有效解;记集值优化问题(S,F)所有E-有效解构成的集合为EEff(S,F)。 定义6 设E∈ξY,y∈F(S),若存在满足C{0}⊂intC1的内部非空的尖闭凸锥C1,使得(F(S)+E-{y})∩(-C1{0})=∅,则称点y为集合F(S)的E-Henig有效点;记F(S)所有E-Henig有效点构成的集合为EHMinF(S);若x0∈S,存在y0∈F(x0),使得y0∈EHMinF(S),则称点x0为集值优化问题(S,F)的E-Henig有效解;记集值优化问题(S,F)所有E-Henig有效解构成的集合为EHEff(S,F)。 注1 若取E=ε+C{0},其中ε∈C{0},此时E-Henig有效点退化为ε-近似Henig有效点;若取E=C{0},此时E-Henig有效点退化为Henig有效点。因此E-Henig有效点统一了Henig有效点及ε-近似Henig有效点概念。 命题1[7,17]若E∈ξY,intE≠∅,A⊂Rl为非空子集,则以下性质成立: (1) intE∈ξY,intE=E+intC,intE=cl(E)+intC。 (2) 若E⊂C,则E+E⊂E,E+intE⊂E,且coneE为凸的。 (3) 若intC⊂E⊂C{0},则有clcone(A+C) =clcone(A+E)。 (4)clcone(A+E)=clcone(A+intE),clcone(A+E)+C=clcone(A+E)。 注2 结合命题1中(1)易得,EWMinF(S)⊃ EMinF(S)⊃EHMinF(S)。 下面介绍紧集值映射、集值映射凸性、集合Painlevé-Kuratowski(简记P.K.)收敛,以及集值映射序列Painlevé-Kuratowski收敛的概念及相关性质。 定义7[16]设F:S→2Rl为集值映射,若对任意x1,x2∈S,λ∈[0,1],有 λF(x1)+(1-λ)F(x2)⊂F(λx1+(1-λ)x2)+C 则称集值映射F为C-凸集值映射。 定义8[16]设F:S→2Rl为集值映射,若对任意x1,x2∈S,x1≠x2和任意λ∈(0,1),有 λF(x1)+(1-λ)F(x2)⊂F(λx1+(1-λ)x2)+intC 则称集值映射F为严格C-凸集值映射。 定义9[18]设F:S→2Rl为集值映射,若对任意x1,x2∈S,λ∈[0,1],有下式之一一定成立: F(x1)⊂F(λx1+(1-λ)x2)+C F(x2)⊂F(λx1+(1-λ)x2)+C 则称集值映射F为真拟C-凸集值映射。 定义10[18]设F:S→2Rl为集值映射,若对任意x1,x2∈S,x1≠x2和任意λ∈(0,1),有下式之一一定成立: F(x1)⊂F(λx1+(1-λ)x2)+intC F(x2)⊂F(λx1+(1-λ)x2)+intC 则称集值映射F为严格真拟C-凸集值映射。 定义11[18]设F:S→2Rl为集值映射,若对任意x1,x2∈S,y1∈F(x1),y2∈F(x2)和任意λ∈[0,1],存在η∈[0,1],使得ηy1+(1-η)y2∈F(xλ)+C,则称F为自然拟凸集值映射。 定义12[18]设F:S→2Rl为集值映射,若对任意x1,x2∈S,x1≠x2,y1∈F(x1),y2∈F(x2)和任意λ∈(0,1),存在η∈[0,1],使得ηy1+(1-η)y2∈F(xλ)+intC,则称F为严格自然拟凸集值映射。 注3[18]若F是严格真拟C-凸集值映射,则F也是真拟C-凸集值映射;若F是真拟C-凸集值映射,则F也是自然拟凸集值映射。然而真拟C-凸性与C-凸性没有必然联系。 定义13[16]设α∈Rl,F:S→2Rl为集值映射;F在高度α下的水平集Fα定义为Fα={x∈S:α∈F(x)+C}。 注4[16]1) 对任意α∈Rl,当F是自然拟凸集值映射时,Fα是凸集; 2) 结合注3可知,当F是严格真拟C-凸集值映射或真拟C-凸集值映射时,Fα也是凸集。 定义14[14]设S⊂Rm是闭凸集合,S的回收锥集合定义为0+(S)={d∈X:x+td∈S,∀x∈S,∀t≥0}。 注5 显然,对于闭凸集合S⊂Rm,0+(S)= {0},当且仅当S为有界集。 定义15[19]设F:S→2Rl为集值映射,若对任意x∈S,F(x)是Rl上的紧子集,则称集值映射F在S上是紧值的。 定义16[20]若Rm中非空凸集S的边界(简记为∂S)不包含线段,则称S是rotund的,即对任意x,x′∈S,x≠x′,有]x,x′[∩(∂S)c≠∅,其中,]x,x′[={λx+(1-λ)x′:λ∈[0,1]}。 定义17[16]设F:S→2Rl为凸值映射,若对任意x∈S,F(x)是rotund子集,则称F在S上是rotund值的。 注6[16]若F是单值映射,则F在S上既是rotund值,又是紧值。 引理1[19]设F:S→2Rl是集值映射,x0∈S,若F在S上是紧值的,F在x0处上半连续(简记u.s.c),则对任意S中的序列{xn}有xn→x0,且对任意yn∈F(xn),存在y0∈F(x0)和{yn}中的子序列{ynk},使得ynk→y0。 本节在集值优化问题可行域和目标映射均扰动的情况下,建立了集值优化问题E-Henig有效解点集和解集的稳定性结果。从下面开始,总假设E∈ξY。 引理2 设S⊂Rm是非空闭凸子集,F在S上是上半连续的真拟C-凸紧值集值映射,若α∈Rl,Fα≠∅,则有Fα是闭凸集。 证 明结合注4可知,对α∈Rl,若Fα≠∅,则显然有Fα是凸集。下证Fα是闭集:令xn∈Fα且xn→x,因为xn∈S,S为闭集,所以x∈S;由xn∈Fα可知,存在yn∈F(xn),使得α∈yn+C;又由引理1可知,{yn}中存在子序列{ynk},使得ynk→y且y∈F(x),从而有α∈F(x)+C。因此x∈Fα,即Fα为闭集。 d(xnk,Fα)>r (1) 当{xnk}无界时,不妨设(如果有必要可选择合适的子序列) ‖xnk‖→∞ (2) 设对任意t≥0,有 (3) (4) 因为γnk→α,所以对任意ε∈intC,存在kε∈N,使得 α+ε∈γnk+C,∀k≥kε (5) 由Fnk的真拟C-凸性可知,对任意λ∈[0,1],下式之一一定成立 Fnk(xnk)⊂Fnk(znk)+C (6) (7) 综上,式(1)不成立,求证成立。 命题3 设S⊂Rm为非空闭凸子集,F:S→2Rl为S上的上半连续真拟C-凸集值紧值映射,epiF为闭集,则以下命题等价: 1)α∈Rl,当Fα≠∅时,0+(Fα)={0}。 2)α∈Rl,当Fα≠∅时,Fα有界。 证 明2)⟹1)。用反证法:若存在x∈0+(Fα)且x≠0,则有 a+tx∈Fα,∀a∈Fα,∀t≥0 (8) 因为Fα≠∅,取l∈Fα,由式(8)可知,l+tx∈Fα,∀t≥0,这意味着Fα无界。 α∈y+C (9) α∈yn+C (10) 由F的真拟C-凸性可知,y∈F(zn)+C或yn∈F(zn)+C一定成立。当y∈F(zn)+C时,由式(9)可知,α∈F(zn)+C,即zn∈Fα;当yn∈F(zn)+C时,由式(10)可知,α∈F(zn)+C,即zn∈Fα;因此存在F(zn)中的序列{wn},使得α-wn∈C。由引理1可知,存在{wn}中的子序列{wnk},使得wnk→w且w∈F(z),从而有α-w∈C,这意味着α∈F(z)+C,即z∈Fα。因此x0≠0且x0∈0+(Fα),这与0+(Fα)={0}相矛盾。 xk∈Snk,γk∈Fnk(xk)+C (11) (xk,γk)→(x,γ) (12) 由式(12)可知,γk→γ,所以对任意ε∈intC,存在kε∈N,使得 γ+ε∈γk+C,∀k≥kε (13) 结合式(11)和式(13)可知,γ+ε∈Fnk(xk)+C,∀k≥kε。这意味着,当k充分大时,有 (14) 接下来,在集值优化问题的可行域和目标映射均扰动的情况下,建立集值优化问题E-弱有效点集和E-Henig有效点集的稳定性结果。 命题5 设E=C1{0},(F(S)-{y})∩(-C1 {0})=∅,则(F(S)-{y}+E)∩(-C1{0})=∅。 证 明任取x∈F(S)-{y},由(F(S)-{y})∩ (-C1{0})=∅,可知x∉-C1{0},即x∈Rl (-C1{0}),从而 F(S)-{y}+C1{0}⊂Rl(-C1{0})+C1{0}⊂ Rl(-C1{0}) 即(F(S)-{y}+C1{0})∩(-C1{0})=∅。因为E=C1{0},所以(F(S)+E-{y})∩(-C1{0}) =∅。 注7 由命题5可知,当E=C1{0}时,Henig有效解一定是E-Henig有效解。 定理2 设F:S→2Rl和Fn:Sn→2Rl为上半连续严格真拟C-凸的紧值集值映射,且满足命题2中其余的条件,若C是满足C{0}⊂intC1的尖闭凸锥,epiF为闭集,intC⊂intE,E=C1{0},F在S上为rotund值映射,则有limnsupEHMinFn(Sn)⊂EHMinF(S)。 证 明任取y∈limnsupEHMinFn(Sn),下证y∈EHMinF(S)。因为 limnsupEHMinFn(Sn)⊂limnsupEWMinFn(Sn)⊂ EWMinF(S)⊂F(S) -C1{0}-C1{0}⊂ -C1{0}-C1⊂ -C1{0} (15) (16) (17) 若xnk≠unk,由Fnk的严格真拟C-凸性可知,有Fnk(xnk)⊂Fnk(sk)+intC或Fnk(unk)⊂Fnk(sk)+intC之一成立。因为ynk∈Fnk(xnk)且ynk∈EHMinFnk(Snk),所以 (Fnk(Snk)+E-{ynk})∩(-C1{0})=∅ (18) 又因为C{0}⊂intC1,所以由式(18),可知(Fnk(Snk)+E-{ynk})∩(-intC)=∅;进一步,有 ynk∉Fnk(Snk)+E+intC (19) 由命题1中(1)可知,E+intC=intE,结合intC⊂intE和式(19),可知 ynk∉Fnk(Snk)+intC (20) (21) (22) 由命题1中(1) 可知,E+intC=intE,从而有y′-ε∈y-intE;又由y′-ε∈F(x)可知,有y′-ε∈F(x)∩(y-intE),这与y∈EWMinF(S)相矛盾。 综上由(1)和(2)可知,y∈EHMinF(S),limnsupEHMinFn(Sn)⊂EHMinF(S)。 其次,建立扰动真拟C-凸集值优化问题E-Henig有效解集的稳定性结果。 (23) (24) (25) 由式(24)和式(25)可得,当k充分大时,有 (26) Fnk(xk)⊂Fnk(vk)+intC (27) Fnk(uk)⊂Fnk(vk)+intC (28) (29) 由命题1中(1)可知,E+intC=intE,从而有y′-ε∈y-intE;又由y′-ε∈F(x)可知,有y′-ε∈F(x)∩(y-intE),因为EHMinF(S)⊂EWMinF(S),所以y∈EWMinF(S),这与y′-ε∈F(x)∩(y-intE)相矛盾。因此x∈EHEff(S,F)。 有关集值优化问题“解”的研究一直是最优化理论与方法的研究热点之一,关于集值优化问题E-Henig有效解的性质和稳定性研究较少。本文利用Painlevé-Kuratowski收敛性,建立集值映射水平集的闭凸性、有界性及回收锥的相关性质,然后借助所获得的集值映射水平集的闭凸性、有界性及回收锥的性质,在集值优化问题目标映射和约束条件均扰动的情况下,分别建立严格真拟C-凸集值优化问题E-弱有效点集、E-Henig有效点集和E-Henig有效解的稳定性结果。该结论大大完善了集值优化问题Henig有效解理论,并为数值计算的稳定性分析提供了方法和技巧。
3 稳定性结果



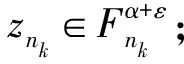
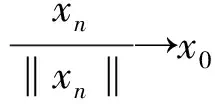

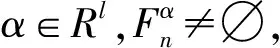

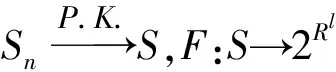
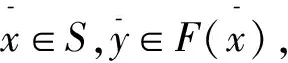
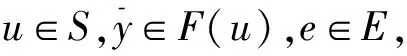

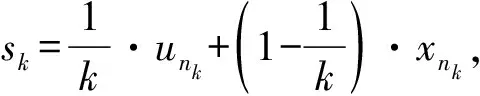
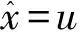
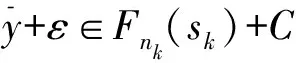
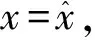
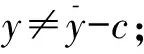
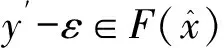

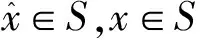


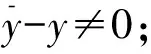

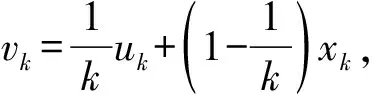
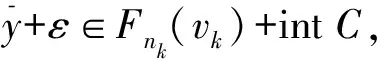
4 结 论
