求解非线性方程组的HHHO算法及工程应用
2023-07-03洪丽啦莫愿斌鲍冬雪
洪丽啦,莫愿斌*,2,鲍冬雪
(1. 广西民族大学人工智能学院,广西 南宁530006;2. 广西民族大学广西混杂计算与集成电路设计分析重点实验室,广西 南宁530006)
1 引言
现实生活中很多问题的求解,最终都可以归结为求解复杂非线性方程组,由于非线性方程组的求解具有一定的复杂性,如何有效的获得方程组的精确解及全部解成为了一个研究目标,在群智能优化算法未被广泛地应用于求解优化问题前,线性方程组的求解大多依赖于传统的求解方法,例如,牛顿法、迭代法、最速下降法、单纯型法等,但是这些方法对目标函数的初始值具有很强的依赖性和敏感性。与传统的求解方法相比,群智能优化算法能够在全局范围内对最优值进行自适应、自动地向个体最优值学习追踪目标解,不依赖于初始值,且对目标函数是否可导不做限制。因此,用群智能优化算法求解非线性方程组成为了一个研究方向,目前已经有很多学者把智能优化算法应用于非线性方程组的求解,如文献[1]的和声搜索算法,文献[2]的蝴蝶优化算法、文献[3]的混合布谷鸟算法、文献[4]的差分进化算法,文献[5]的BFGS差分进化算法等,虽然智能优化算法计算速度快,但是存在求解精度低,求解根的个数不完全,收敛速度慢等问题,针对以上存在的问题,本文提出一种改进的混合哈里斯鹰优化算法用于求解非线性方程组,首先,在全局阶段,采用二次插值这种二次拟合的方式,增强了算法的全局寻优能力,加快了搜索速度,其次,当算法迭代到后期时容易陷入局部最优,根据差分进化算法具有良好的全局探索能力,将差分进化中的变异、选择操作引入到局部搜索阶段,使算法增强摆脱陷入局部最优的能力,最后,通过把HHHO算法用于解决几何约束问题,结果说明HHHO算法在求解精度具有一定的优势。
2 非线性方程组
非线性方程组的数学模型如下
其中,m代表变量的个数,n代表求解方程的个数,可以将方程组的求解转换成目标函数,形式如下:
求解A(X)的根等价于求解非线性方程组的各个解。
3 哈里斯鹰优化算法
哈里斯鹰优化算法[6](Harris hawks optimization,HHO)是于2019年Heidari 等人通过模拟哈里斯鹰的捕食行为而提出的一种启发式智能优化算法,哈里斯鹰围攻猎物可分为两个阶段,勘探阶段和开发阶段,勘探阶段主要是对猎物进行等待和监视,开发阶段对猎物进行抓捕,在开发阶段根据不同策略对猎物进行围攻,每个阶段详细的过程如下。
3.1 勘探阶段
在勘探阶段,哈里斯鹰主要通过两种概率相等的策略对猎物进行监视。

(1)
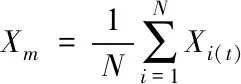
(2)
其中,Xrand(t)代表当前种群中的一个随机位置,Xrabbit(t)代表猎物的位置,即当前最优解,Xm(t)代表当前种群位置的平均值,r1,r2,r3,r4,q均为0到1的随机数,UB和LB分别为种群的上下界,N为种群数量。
3.2 勘探阶段向开发阶段的转换
勘探阶段转成开发阶段是通过猎物的逃跑能E来控制,当能量的绝对值大于等于1,则进行全局搜索,当能量的绝对值小于等于1,则进行局部搜索。

(3)
其中,E0为猎物的初始状态,E0∈(-1,1),t为当前迭代次数,T为最大迭代次数。
3.3 开发阶段
1)软围困
当r≥0.5且|E|≥0.5时,此时猎物有足够的能量并且想通过随机的跳跃逃跑,哈里斯鹰将其轻轻包围,进行突袭,其数学公式如下
X(t+1)=ΔX(t)-E|JXrabbit(t)-X(t)|
(4)
ΔX(t)=Xrabbit(t)-X(t)
(5)
J=2(1-r5)
(6)
其中,ΔX(t)是猎物的位置向量与当前迭代t中的个体向量的差值,J表示猎物在逃离哈里斯鹰围困的过程中的跳跃程度,r5∈(0,1)。
2)硬围困
当r≥0.5且|E|<0.5时,此时猎物已经非常疲惫,没有足够的能量逃跑,哈里斯鹰将其进行硬围困,其数学公式如下
X(t+1)=Xrabbit(t)-E|ΔX(t)|
(7)
3)软性包围和渐进式快速俯冲
当r<0.5且|E|≥0.5时,猎物有足够的能量逃脱包围圈,此时哈里斯鹰根据猎物(尤其是兔子)的欺骗性动作变换抓捕的位置和方向,对猎物形成一个包围圈并进行快速俯冲围困,其数学公式如下
Y=Xrabbit(t)-E|JXrabbit(t)-X(t)|
(8)
Z=Y+S×LF(D)
(9)

(10)

(11)

(12)
其中,D为种群的维度,S为1×D的随机向量,LF为莱维飞行函数,μ和v是0到1的随机数,β取值为1.5。
4)使用渐进的快速俯冲进行猛烈的围攻
当r<0.5且|E|<0.5时,猎物没有足够的能量逃跑,此时老鹰通过缩小与猎物的平均位置距离,形成一个很小的包围圈来抓捕猎物,其数学公式如下
Y=Xrabbit(t)-E|JXrabbit(t)-Xm(t)|
(13)
Z=Y+S×LF(D)
(14)

(15)
4 混合哈里斯鹰优化算法
4.1 引入二次插值
在勘探阶段,由于哈里斯鹰的初始位置是在解空间中随机产生的,且哈里斯鹰寻找猎物是通过从解空间中随机的同伴来获取信息,对目标的信息量获取较少,因此不容易找到目标,导致寻优能力降低,为此在勘探阶段引入二次插值算子[7]式(16),二次插值是一种曲线拟合方法,通过在解空间中构造低次多项式的解来不断的替换逼近原目标函数,以此来更快的求得目标函数的解。
在每一次迭代的勘探阶段,在种群中随机的选择两个哈里斯鹰的位置作为二次插值的区间,根据式(16)求出二次曲面的极小值作为当前最优值,把得到的最优值和种群的最优值进行比较,选择较好的作为当前迭代的最优个体,通过这种策略,可以使种群更快的向最优个体靠拢,以此来提高算法的全局搜索能力。
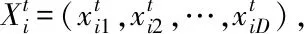

(16)


(17)
4.2 结合差分变异机制
经过追逐奔跑,猎物的逃跑能量渐渐衰弱,处于被围困状态,此时哈里斯鹰聚集在猎物(最优个体)周围,但如果当前猎物的位置为局部极值,那么哈里斯鹰就容易陷入局部最优,即出现“早熟”现象,不利于种群向更优的个体进化,导致算法在解空间的求解精度降低。因此需要采取策略来改变哈里斯鹰的过度聚集,即需要增强种群的多样性,使部分哈里斯鹰朝着解空间其它地方搜索,以此来增强哈里斯鹰挣脱陷入局部最优的能力,从而提高算法的求解精度。
根据早熟机制[8],当种群满足早熟条件,说明种群多样性变差,此时需要采取一定的手段来改善种群的多样性。差分进化[9]是一种具有较强的全局搜索能力的智能优化算法,其主要是依靠种群之间的竞争与合作行为来完成信息的共享与交流,首先,对父代种群进行变异、交叉操作得到子代,其次,根据贪婪选择机制,选择较优的个体作为当代的新一代群体。差分进化有五种变异策略,采用了DE/best/1,具体的形式如下
DE/best/1:Vi(t)=Xbest(t)+F(Xr1(t)-Xr2(t))
(18)
其中,Xbest(t)为本次迭代的最优个体,Xr1(t) 和Xr2(t) 是当前迭代种群中的不同的个体,F是变异系数,其值设为0.4,通过该变异式子加强种群间的信息共享,通过个体之间的交叉组合,可以增强哈里斯鹰种群的多样性,使陷入早熟的哈里斯鹰有机会朝着其它解空间继续搜索其它潜在解,然后在再根据选择操作保留下优质个体,选择操作如下

(19)
4.3 HHHO算法步骤
1)初始化相应的参数并给种群赋初值;
2)根据式(3)计算出猎物的逃跑能量E;
3)计算种群的适应度函数、均值,找出种群的最优个体;
4)若|E|≥1,则采用式(1)-(2)对种群进行全局搜索。
5)若|E|<1,根据以下条件对种群进行局部开发,并用式(16)-式(17)进行二次插值。
a)若r≥0.5且|E|>0.5时,采用式(4)-(6)对种群进行局部开发;
b)若r≥0.5且|E|<0.5时,采用式(7)对种群进行局部开发;
c)若r<0.5且|E|≥0.5时,采用式(8)-(12)对种群进行局部开发;
d)若r<0.5且|E|<0.5时,采用式(13)-(15)对种群进行局部开发;
6)根据早熟机制,若算法陷入局部最优,则采用式(18)-式(19)对进行变异、选择操作。
7)判断是否达到最大迭代次数,若没有达到最大迭代次数,则反复执行3)-6),直到满足最大迭代条件为止。
4.4 算法伪码
Begin
Initialize algorithm parameters and generate initialization population
X={Xij,i=1,2…N,j=1,2…N}
Calculate escape energyE
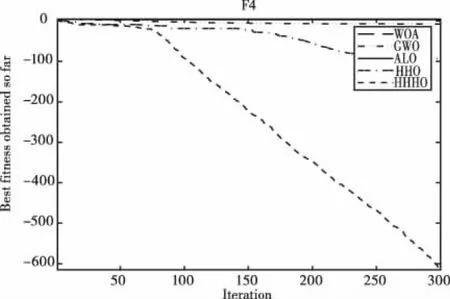
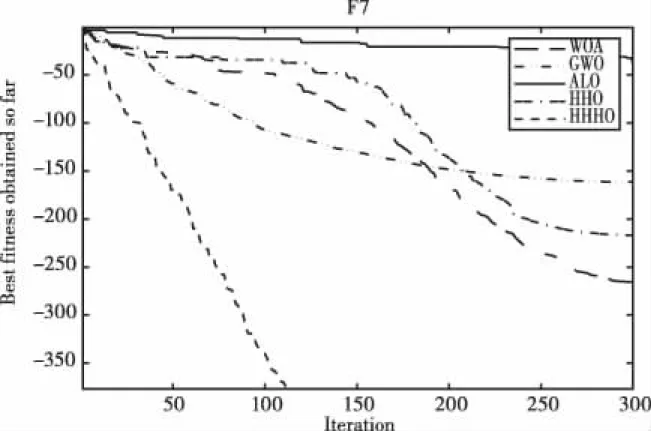
While t for i=1 to N do The fitness value of population is calculated to find out the optimal individual if(|E|>1)do Update the position according to equations (1)and (2) else if (|E|<1)do if(r≥0.5&&|E|>0.5)do Update the position according to equation (4) if(r≥0.5&&|E|<0.5)do Update the position according to equation (7) if (r≥0.5&&|E|≥0.5)do Update the position according to equations (8)-(12) if(r<0.5&&|E|<0.5)do Update the position according to equations (13)-(15) end if end for t=t+1; end while end 为了测试HHHO算法的性能,本文选取了10个基本测试函数对算法进行测试,测试函数如表1所示。 表1 标准函数测试 为了验证混合哈里斯鹰优化算法性能的有效性和可行性,本文将HHHO算法和HHO,WOA,GWO,ALO四种算法同时对同一个测试函数进行测试分析,种群规模设置为30,最大迭代次数为300,为了验证算法的稳定性和鲁棒性,将算法独立运行30次,计算出每种算法测试的最优值、最差值、平均值,实验数据如表2-表3所示,为了更直观的观察算法的收敛效果,画出了效果收敛图如图1-图10所示。 图1 函数f1的收敛图 图2 函数f2的收敛图 图4 函数f4的收敛图 图5 函数f5的收敛图 图6 函数f6的收敛图 图7 函数f7的收敛图 图8 函数f8的收敛图 图9 函数f1的收敛图 图10 函数f10的收敛图 表2 实验数据(1) 表3 实验数据(2) 本文将HHHO算法和WOA、GWO、ALO、HHO四种算法进行比较,首先,由表2-表3可知,HHHO算法对f1,f3,f4,f7,f8,f10能搜索到理论最优值0,且平均值和标准差都是0,可以看出HHHO具有较高的稳定性,而对于函数f5,f6,f9虽然在300次迭代中不能搜寻到最优值,但是和其它四个算法相比而言,求解精度是最高的,而对f2函数HHHO和HHO具有相同的求解精度。其次,从图1、图2、图7、图8的收敛曲线可以直观的看出HHHO在前期的收敛速度较快,证明了二次插值提高了HHO在高维空间的搜索能力。 采用5个非线性方程组进行测试,种群规模设置为30,迭代次数设置为800次,每个方程组独立运行10次取平均值,实验结果如表4-表8所示。 表4 方程组1结果比较 表5 方程组2结果比较 表6 方程组3结果比较 其中,-1≤x1,x2≤1,理论值x*=(1,1,1),x*=(-1,-1,-1) 其中,-1≤x1,x2≤1,理论值x*=(0,1) 其中,-1.732≤x1,x2,x3≤1.732,理论值x*=(1,1,1) -100≤x1,x2≤100,理论值为x*=(10,1)和x*=(-7.5,1) 其中,-2≤x1,x2≤2,该方程有10个解,分别是:(-1.81089,-0.34909),(-1.81089,0.34909),(-1.50222,-0.40908),(-1.50222,0.40908),(-1.79130,0.30193),(-1.791330,-0.30193),(-0.94724,0.78502),(-0.94724,-0.78502),(-0.21306,-1.25685). 由表4-6可知,HHHO算法相比于文献[10]在种群规模为100时具有更高的求解精度,且能够搜索到理论最优值,由表4可以看出,文献[11]只能搜索到一个解,而HHHO能够求到两个精确解,由表7可知,HHHO算法能够获得方程组的理论解,但是方程组的值比文献[11]略差了点,由表8可知,HHHO算法能够求得方程的10个根,并且与理论值接近,虽然文献[11]也能求到这个值,但是种群规模却比HHHO的种群规模大得多。综上,HHHO算法在求解精度及求解速度方面都具有一定的优势。 表7 方程组4结果比较 表8 方程组5结果 图11 几何约束模型 x-y-100=0 (20) (21) 通过仿真,求得方程组(21)的解如表9所示。 表9 仿真求得方程组(21)的解 表10 文献[14]和HHHO两算法求解比较 三角函数超越方程[14]的零点求解对许多机械问题具有重要的求解意义,由于其庞大的数值解成为了研究的一个热门和难点,本文采用HHHO算法来求解三角函数超越方程,其表达式如式(22)所示,其中,x1∈[-3π/2,3π/2],x2∈[-π,2π]。 (22) 通过把HHHO算法应用在几何约束问题和三角函数超越方程中,从实验数据可以看出,相比于文献[13],HHHO算法求解出来的值更接近于理论值,相比于文献[14]采用的同伦法求解三角函数超越方程,HHHO算法求出了18个近似的解,并且解能精确到10位数,相对于文献[14],HHHO算法的求解精度更高,因此可以看出HHHO算法具有较高的求解性能,对工程应用具有一定的实际意义。 针对HHO算法在前期搜索速度慢,且由于在进化后期随着种群多样性减少,导致算法容易陷入局部最优等缺陷,提出一种基于二次插值和差分进化优化算法的HHHO算法,通过10个测试函数和5个非线性方程组的测试结果比较分析,验证了HHHO算法在求解精度、避免算法陷于局部最优、收敛速度快等方面都具有良好的表现,证明了算法的全局探索能力和局部开发能力得到了改进。最后,将HHHO算法应用于求解几何约束问题和三角函数超越方程,并且得到了满意的求解结果。5 仿真与结果分析
5.1 测试函数

5.2 测试结果









5.3 测试结果分析
6 算法用于求解非线性方程组



6.1 非线性方程组




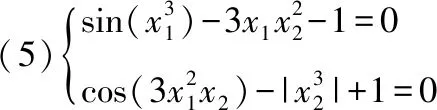
6.2 测试结果
6.3 测试结果分析

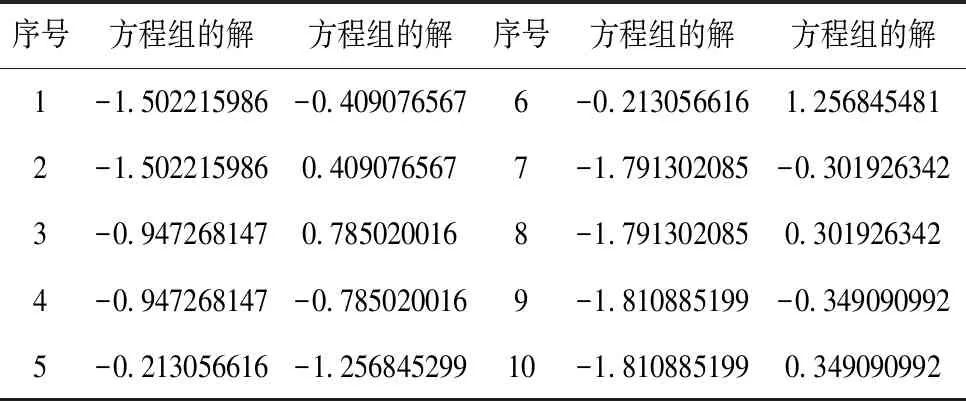
7 算法在工程上的应用
7.1 几何约束问题





7.2 三角函数超越方程

8 结语
