基于改进鱼群算法的双向式立体库货位优化研究
2023-07-03范贤光吴俊涛尹艺玲许英杰
范贤光,吴俊涛,尹艺玲,许英杰
(厦门大学航空航天学院,福建 厦门 361100)
1 引言
据统计,企业产品制造过程中,有90%时间消耗在物流仓储过程中,其成本占用总生产制造成本的10%,因此,对物流仓储过程的优化是提高企业效益[1]的重要途径,而物流仓储的重要环节之一便是货位分配。传统的货位分配[2][3]模式往往是简单的人工进行就近放置,对于大信息量或者动态变化的订单数据时将耗费大量人工,增加企业生产成本。基于数字化背景下[4]的货位优化,能动态的根据货物的相关属性、立体库内资源占用情况、运行效率和人工成本等因素实现最佳的分配,极大降低生产成本提高运行效率,进而为企业带来直接的经济效益。随着企业的规模扩大和对立体库灵活性要求的提高,多巷道双向式结构更优于传统的单出入口模式,既能够灵活配置货物的出入口又提高了运行效率,极具研究意义。
基于数字化平台下的货物仓位分配问题,国内外学者已经进行了大量的研究,并取得了一定的科研成果。Li[5]和焦玉玲[6]以提高货物出入库率、货架稳定性以及关联性货物就近存储作为研究目标,分别采用遗传模拟退火算法以及层次分析配合遗传算法进行优化,Yang[7]考虑以提高出入库效率以及货架稳定性作为研究目标,采用蚁群算法进行寻优计算,张磊[8]以仓库利用率最大化和仓库稳定性最优化为数学模型,采用多种群遗传算法进行计算,虽然他们的算法取得了较好的结果,但是在实际立体仓库中,会有多排货架的配置,文章内容未提及平衡各巷道工作量的要素,可能会造成系统资源利用率不高的问题;唐文献[9]和吴炳[10]以提高出库效率,降低货架中心以及平衡各巷道工作量作为目标函数,分别采用细菌觅食算法和模拟退火遗传算法进行优化,取得了良好效果;马永杰[11]以库区分配、货位分配以及行使时间作为优化目标,采用遗传算法进行求解,取得一定成效,肖建[12]以物料相关性及需求频率为优化目标,采用遗传算法进行寻优,实验结果也符合预期,上述研究都是基于单出入口的立体仓库模型,而蔡安江[13]等基于双向式立体仓库模型,建立以出入库效率、货品相关性以及货架稳定性为目标函数,采用混合蛙跳算法进行计算,取得了良好效果,但对于常见的多巷道系统无法很好适用。
因此,本文将多巷道双向式的立体仓库作为研究对象,以提高出入库效率和平衡各巷道工作量为目标函数,采用基于平均距离视野的自适应人工鱼群算法(Adaptive Artificial Fish-swarm Algorithm1,AAFSA1)进行寻优,优化了货物在立体仓库内的位置分配,解决巷道的工作量不均衡问题,从而提高整套系统的工作效率。
2 立体库系统描述
多巷道双向式的立体库模型配置多排货架和巷道,巷道架设在货架中间,巷道上运行着一台码垛机,其作用主要用于货物的出入库操作,每条巷道两端设置有一个货物的出入库台。企业可以根据需求增减货架和巷道数量。系统结构俯视图如图1所示。

图1 系统结构俯视图
为了方便算法研究,做出如下说明:
1)每个仓位放置一个仓盒,码垛机在出入库台和货架之间来回运输仓盒。
2)订单信息与仓盒绑定,当订单信息内货物数越多,该仓盒就需要频繁出入库接收新的货物。
3)定义系统结构俯视图货架右下角底部为位置原点,每条订单在货架的位置信息可以表示为(x,y,z),其中x表示在货架第x排,y表示第y列,z表示第z层。
4)货架有a排,b层,c列,仓位深度为d,宽度为w,高度为h。
5)码垛机总是处于匀速运行状态,水平、垂直货叉速度分别为Vx,Vy,Vz。
在实际的生产中,出现订单集中存放、出入库率高的订单没有靠近出入库台、个别巷道的工作量繁重,其它巷道的工作量极低甚至没有工作量的现象。
为了解决上述问题,实现立体库运行效率最大化,让各巷道工作量均衡的目的,本文提出如下订单仓位优化和分配原则:
1)提高货物出入库效率。在仓位分配时,要考虑出入库率高的订单靠近出入库台,这样极大减少码垛机的运行时间,以提高货物出入库率继而提高整套系统工作效率。
2)均衡各巷道的工作量。大型仓储系统普遍拥有多条巷道,在仓位分配时,需要充分考虑各巷道的工作情况,合理的将工作量分配到各巷道上,实现资源利用最大化。
3 仓位分配数学模型
每条订单信息有如下参数信息:(x,y,z,pxyz,pos),其中:(x,y,z)表示该订单分配到立体仓库货架的位置信息,pxyz表示该订单在系统内的出入库次数,pos表示该订单的出入库口,pos有两个值:pos=0或者pos=b+1;当pos=0时,表示该订单的出入库口为巷道的右边,当pos=b+1时,表示订单的出入库口为巷道的左边。
1)提高货物出入库效率
将每条订单尽量安排在靠近出入库口侧,且考虑订单的出入库次数,让出入库次数高的更靠近出入库口,以此减少码垛机的运行时间,提高工作效率。建立的目标函数是码垛机完成一次入库或者出库时间与该订单的出入库次数的乘积。码垛机在完成入库或者出库动作时,水平y与垂直z方向的运动是同时的,将仓盒送入货架内是独立运动,因此,所设计目标函数为
F1(x,y,z)=
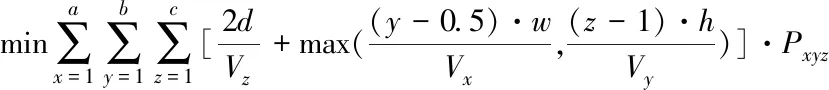
(1)
2)平衡各巷道工作量
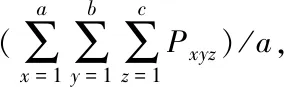

(2)
x,y,z均为正整数。
3)评价函数
所建立的系统模型是一个多目标函数,且各自目标函数量纲不同,但又相互影响,所以采用最优值法对上述两个目标函数进行处理。首先,对各目标单独运算,求出其收敛后的最优值F′(x,y,z),然后根据实际值与最优值之间的平方差构造评价函数Fi=[F(x,y,z)-F′(x,y,z)]2。引入比例系数∂i,可将多目标函数转换为评价函数:

(3)
4 基于平均距离视野的自适应人工鱼群算法设计
基于平均距离视野的自适应人工鱼群算法是一种新的群智能优化算法,该算法最早由李晓磊[14]博士于2002年提出,主要模拟鱼在水中的追尾、聚群、觅食以及随机行为来实现寻优目的,具有并行性、简单性、能很快跳出局部极值、寻优快的特点。传统人工鱼群(Artificial Fish-swarm Algorithm,AFSA)在追尾、聚群以及觅食[15]的过程中,需要在其感知距离Visual内(视野)选择伙伴,并且通过移动步长Step、拥挤度因子δ来判断是否向伙伴方向移动。
基于平均距离视野的自适应人工鱼群算法,减少了Visual、Step以及δ的初始化设定,通过计算每条人工鱼到其它人工鱼的平均距离,作为自身的感知距离Visual;确定视步系数StepA,将StepA·Visual作为人工鱼的最大移动步长Step。
在算法初期,拥有较大的感知距离Visual和移动步长Step,加强全局寻优能力,有效克服局部极值,在后期,由于人工鱼越来越聚集,使得感知距离Visual和移动步长Step减少,寻优精度会越来越高。
本文中,AAFSA1算法参数定义如下:人工鱼群个体数:FishNum;最大迭代次数:Max_Gen;觅食行为尝试的最大次数:TryNumber;视步系数:StepA;当前迭代次数:NC;当前人工鱼信息:Xi,i为当前代数。算法具体步骤如下:
步骤1:参数初始化,设定FishNum、Max_Gen、TryNumber、StepA。
步骤2:随机生成指定数量的人工鱼,如果待优化的订单数量为30个,则每条人工鱼表示为{x1,x2…x30},x为每条订单的信息,设定i=1。
步骤3:对当前人工鱼Xi执行追尾操作,首先计算当前人工鱼Xi到其它人工鱼的距离平均值,设定为感知距离Visual,以Visual查找身边伙伴,并从找到的伙伴中确定最优鱼Xj,通过适应度函数得到两条鱼的函数值Yi,Yj;如果Yi>Yj,则以Step=StepA·Visual为步长向其方向移动,否则执行觅食行为,最后得到寻优后的信息(Xnext1,Ynext1)。
步骤4:对当前人工鱼Xi执行追尾操作,首先计算当前人工鱼Xi到其它人工鱼的距离平均值,设定为感知距离Visual,以Visual查找身边伙伴,并从找到的伙伴中确定中心位置的鱼Xc,通过适应度函数得到两条鱼的函数值Yi,Yc;如果Yi>Yc,则以Step=StepA·Visual为步长向其方向移动,否则执行觅食行为,最后得到寻优后的信息(Xnext2,Ynext2)。
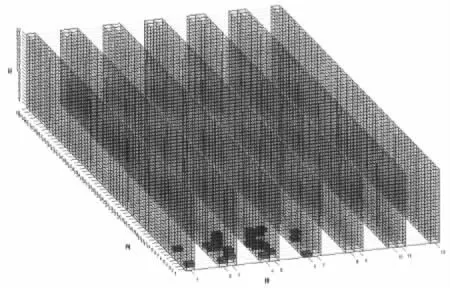
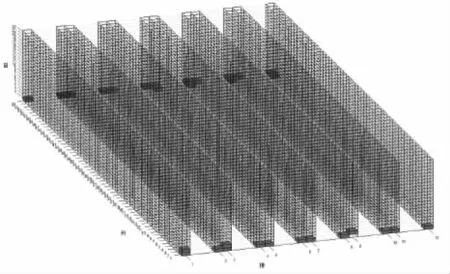
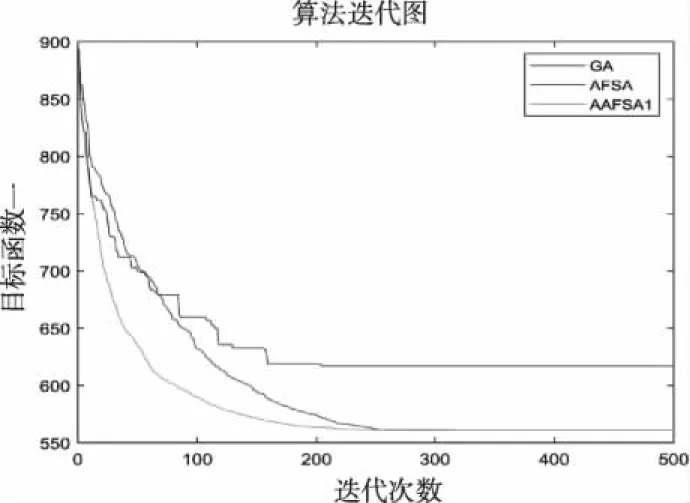
步骤5:比较Ynext1,Ynext2,若Ynext1 步骤6:判断i>FishNum,如果满足,执行步骤7,否则i=i+1,执行步骤4。 步骤7:NC=NC+1,判断NC>Max_Gen,如果满足,执行步骤8,否则执行步骤3。 步骤8:确定最优值,并输出结果。 基于平均距离视野的自适应人工鱼群算法的流程图如图2所示。 图2 基于平均距离视野的自适应人工鱼群算法流程图 以某配件厂为例进行订单仓位分配,立体库各项数据指标如表1所示,订单在立体库的初始信息如表2所示,该信息主要包含订单出入库次数,在立体仓库的位置信息以及对应的出入库台。图3为订单在立体仓库内的初始位置状态,红色块代表每条订单,可以看到,订单在立体仓库内杂乱无章,没有靠近出入库台,且出现了某些巷道无工作量的情况。 表1 立体仓库各项指标 表2 订单初始信息表 图3 优化前各订单在立体仓库内的位置图 本次仿真过程,采用标准遗传算法GA、AFSA以及AAFSA1分别进行优化,以此验证AAFSA1的优势和应用价值。各算法的参数设置说明如表3所示。 当只考虑提高出入库效率为目标函数时,仿真结果如图4、图5所示。当只考虑平衡各巷道工作量为目标函数时,结果如图6、图7所示。可以明显看出,相比图3,图4中订单都被尽量安排到靠近对应的出入库台侧。这样,可以极大减少码垛机的运行时间,达到提高出入库效率的目的。图5中,AAFSA1算法在第220次实现收敛,函数值下降到560.975,GA算法在210次实现收敛,函数值下降到617.1583,AFSA 算法在第 256 次实现收敛,函数值下降到 561.3667。图6中,每条巷道的工作量基本保持一致,充分利用现有巷道资源,达到了各巷道负载均衡的目的。图7中,AAFSA1算法在第8次实现收敛,函数值下降到1.6667,GA算法在235次实现收敛,函数值下降到1.6667,AFSA 算法在第 22 次实现收敛,函数值下降到 1.6667。从图5、图7中的算法迭代图可以明显看出,AAFSA1算法较GA、AFSA算法具有更强的寻优能力,不易陷入局部最优值,且收敛速度更快收敛精度更高。 图4 提高出入库效率的订单位置结果 图5 提高出入库效率的算法迭代过程 图6 平衡各巷道工作量的订单位置结果 图7 平衡各巷道工作量的算法迭代过程 将上述两个单目标函数的最优值以及比例系数∂1=0.85,∂2=0.15带入式子中,建立评价函数如下所示: F(x,y,z)= (4) 建立的评价函数已经消除了各自量纲不同的影响。仿真结果如图8、图9所示。从图8中,可以明显看出订单都被尽量安排到靠近对应的出入库台侧,且每条巷道的工作量基本保持一致。这样,既减少了码垛机运行时间,提高了效率,又充分利用现有巷道资源,达到了各巷道负载均衡的目的。从图9中,AAFSA1在第400代实现了收敛,评价函数值由最先的633.2129下降到1.6749,下降了99.7355%,而GA以及AFSA算法在500代内还未实现收敛。 图8 双目标的订单位置结果 图9 双目标的算法迭代过程 本文基于多巷道双向式的大型立体库货位优化为背景,提出建立提高出入库效率和平衡各巷道工作量为目标函数的数学模型,运用最优值法将多目标函数转换为评价函数。提出AAFSA1算法,减弱了人工设定参数对寻优过程的影响,并通过GA、AFSA以及改进的AAFSA1算法对各自单目标函数和评价函数进行仿真求解,在自寻优过程中可以发现AAFSA1算法具有更快的收敛速度、更强的寻优能力以及更高的精度。优化后的值满足了实际生产需求,大幅提高了企业的生产效率。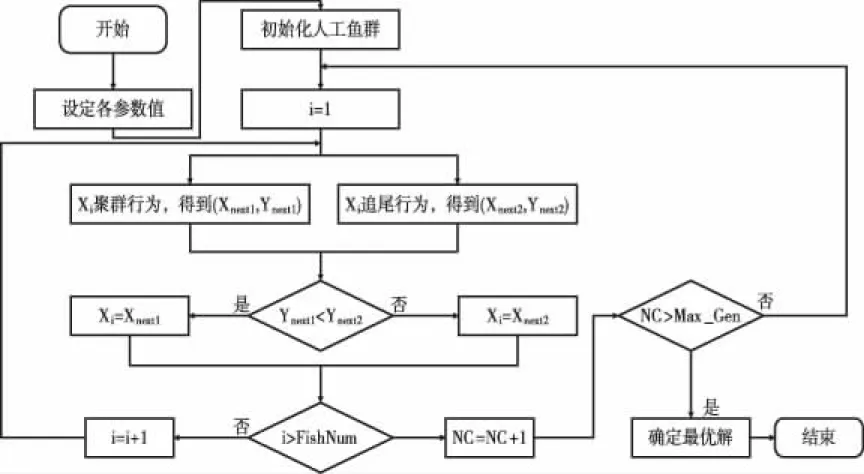
5 算法分析
5.1 数据信息

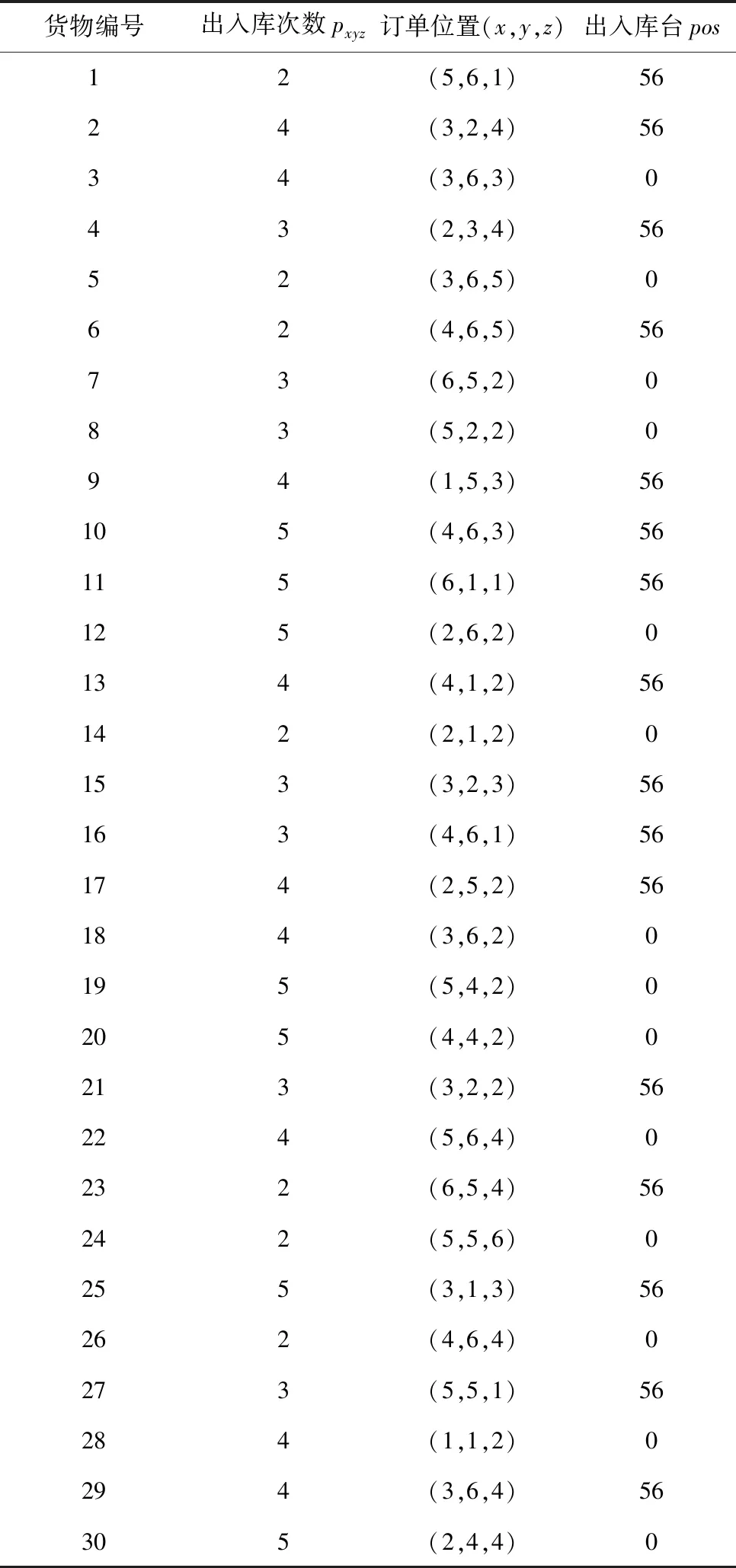
5.2 仿真结果及分析


5.3 双目标的仿真结果及分析
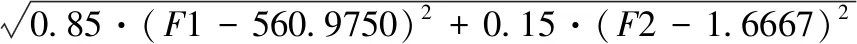


6 结束语
