基于区域中心温度场预测的回流焊接优化仿真

隋 远,卜凡洋,邵子龙,闫 伟

(山东师范大学信息科学与工程学院,山东 济南 250014)

1 引言

元件焊接技术是集成电路板等电子产品生产过程中的一项重要工艺,通过加热元器件达到锡膏熔点后,在液态锡表面张力及助焊剂的作用下锡液回流到元器件引脚上形成焊点,进而完成将线路板焊盘和元件焊接成整体的任务。

实际焊接过程中,工业界往往采用回流焊接工艺,即使用回流焊炉设备,将待焊接元器件传送经过多个不同温区,使锡粉完成由固态到液态再到固态的转换,此过程中锡膏在助焊剂等材料的催化下,融化(锡膏熔点:217℃)形成一层薄薄的锡珠,在其表面张力的作用下,聚集在元器件焊点表面,经冷却区制冷凝固,实现焊接。回流焊接作为集成电路板生产中的关键工序,合理的温度曲线设置是保证回流焊接质量的关键[1]。回流焊接的控制实质上是对温度工艺参数的控制[2],不恰当的温度工艺参数设置会使PCB板出现焊接不全、虚焊、元件翘立、焊锡球过多等焊接缺陷,影响产品质量[14]。

目前,关于温度场工艺参数设定大多通过多次重复实验测试进行控制和调整,测试人员使用传感器等设备获取温区温控曲线,凭借操作人员经验观察得出这条曲线反映的能量作用量以及能量作用点,并依次调整温度场工艺参数。产品质量的好坏直接受到操作员经验的影响。现有的仅通过实验获得符合工艺要求的最佳温度的方法不仅低效,而且在每次实验仅只能获得一组炉温曲线的数据,样本量小,测试结果缺乏普适性,极大的浪费了人力财力物力。

为优化回流焊接工艺参数的调控方法,国内外学者进行了相关研究。目前回流焊温度曲线仿真与预测系统主要以F.Sarvar[6]为代表,提出了部分以机理模型为主要切入点的优化方法[9],[10],徐宗煌[8]提出了一套基于牛顿冷却定律的微分方程的炉温曲线优化模型;席晨曦[11]在微分方程的基础上引入模拟退火算法辅助炉温曲线优化设计;国内的龚雨兵通过数值建模与仿真提出了一种优化的回流焊温度曲线控制;饶庶民[7]在回焊炉温度控制模块的基础上,分析了实际温度场变化规律,使用有限元分析软件对回焊炉内的温度进行仿真分析,可以很好的对温度场进行拟合预测并开发了一套适合回焊炉曲线分析的软件;对于实际回流焊接温度曲线设置,姜海峡[15]论述了回流焊接温度曲线的设置与测试方法,通过对比分析,可调整参数至更加理想的回流焊接温度曲线冯志刚[3]量化了回流焊接工艺参数对温控曲线的影响;张辉华[5]提出了一套面向混装氮气回焊炉的温度曲线控制方案。

为解决传统实验测试方法的弊端,本文采用机理模型进行分析研究,提出一种回流焊接区域中心温度场预测模型,实现区域中心温度场工艺参数的预测优化,并针对特定工业生产场景下的实际需求设计了一套回流焊接优化策略:温度参数已知情况的速度区间预测策略,锡膏融化回流面积最小参数区间预测策略,锡膏融化回流面积左右最对称参数区间预测,能够极大的优化生产过程、节省设备调试时间、优化生产产品焊点质量。

2 基于常微分方程的回流焊接区域中心温度曲线预测模型

2.1 模型定义

通常情况下,回流焊炉内部设置若干个小温区,它们从功能上可分成4个大温区:预热区、恒温区、回流区、冷却区(如图1所示)。某回焊炉内有11个小温区及炉前区域和炉后区域(如图1所示),每个小温区长度为30.5 cm,相邻小温区之间有5 cm的间隙。其中小温区是指具有加热功能的某一连续加热区间,间隙是指没有加热源的某一连续区间,大温区是指由小温区和间隙组合而成的某一连续区间。实验条件下的回焊炉实际尺寸如表1所示。

表1 某回焊炉内含有11个小温区及炉前区域和炉后区域的具体尺寸

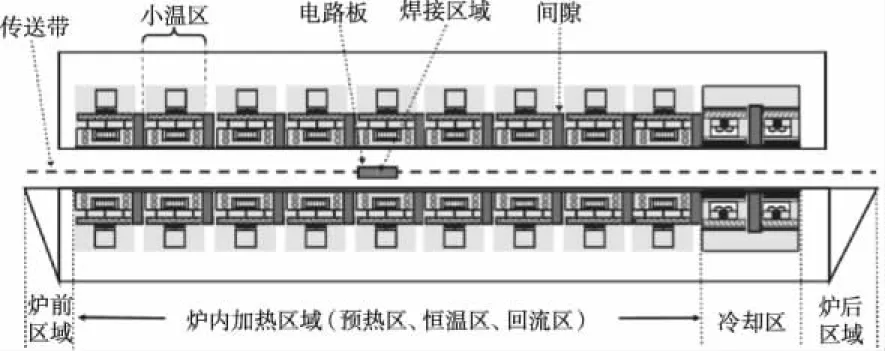
图1 回焊炉截面示意图

参数可调节范围如表2某回焊炉的可调节参数范围所示。

表2 某回焊炉的可调节参数范围

在设定各温区的温度和传送带的过炉速度后,可以通过温度传感器测试某些位置上焊接区域中心的温度,称之为炉温曲线(即焊接区域中心温度曲线)。实际生产时可以通过调节各温区的设定温度和传送带的过炉速度来控制产品质量。在上述实验设定温度的基础上,各小温区设定温度可以进行±10℃范围内的调整。调整时要求小温区1～5中的温度保持一致,小温区8～9中的温度保持一致,小温区10～11中的温度保持25℃。传送带的过炉速度调节范围为65～100 cm/min。

在回焊炉电路板焊接生产中,各温区中心温度场变化应满足一定要求,即制程界限(见表3)。

表3 区域中心温度场变化制程界限

2.2 模型建立

假设焊接区域中心看作质点、焊接系数受温度的影响忽略不计、各加热区设定温度即是对应区域炉内温度、焊接过程不考虑热对流。根据热传导规律(1)以及比热容式(2)对比得出,小温区焊炉内环境温度与焊接中心区域温度的一阶常微分方程(3)

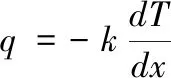
(1)

(2)

(3)

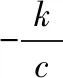
(4)

2.2.1 回流焊炉炉内温度场分布函数T(x)

由于回焊炉相邻小温区之间炉内环境温度场分布符合Sigmoid函数(5),利用此规律,得到平滑的温度过渡曲线如图2所示,曲线两端是恒温区,中间是无加热源的炉内环境温度区,此时Sigmoid函数经过平移变换、伸缩变换后得到T(x)解析式(6)

图2 两端是恒温区,中间是无加热源的炉内环境温度区间过渡曲线

(5)

(6)

针对小温区与小温区之间温差过大的特殊间隙,利用式(4)所述一阶常微分方程推理可知,焊炉内环境温度T(x)与焊接中心区域温度f(x)温差越小,其焊炉内环境温度T(x)的一阶导数越小,因此在TT4=255℃,TT5=25℃且环境温度也为25℃的条件下,凹函数存在下降趋势,由于温差的不断缩小,T(x)的一阶导数也不断减小,此时焊炉内环境温度T(x)必然为凹函数。利用位移与焊炉内环境温度T(x)的直角坐标系易知坐标[x前,TT4],[x后,TT5],代入一阶线性函数可得(7),代入指数函数可得(8),由式(7)(8)可以得到炉内环境温度的线性表达式(9)。

(7)

(8)

T(x)=p·T1(x)+(1-p)·T2(x)

(9)

通过遍历参数p,可以确定当p=0.8时方差最小,不同参数p下炉温曲线与拟合曲线方差见表4。

表4 炉温曲线与拟合数据在不同p下方差

因此,得到炉内环境温度场分布函数如下表5。

表5 炉内环境温度场分布函数

2.2.2 最优焊接系数Q预测

利用传感器等工具,测得得焊接区域中心温度曲线f(x)。将f(x)与炉内环境温度分布T(x)代入式(4)中,设置各个小温区的温度参数以及传送带过炉速度,并将前一区间预测的f(x)的温度末值赋值给后一区间预测的温度初始值,使用四阶龙格库塔法,显式迭代非线性常微分方程,求解出各个位置的解常微分方程的函数值。

通过遍历焊接系数Q,利用作方差等方法挑选出与实验中测得焊接区域中心温度曲线f(x)最为相近的一组温度曲线,确定并评价最优焊接系数并绘制预测曲线。实验显示得出Q=-0.021时方差最小,不同参数Q下炉温曲线与拟合曲线方差见表6。

表6 炉温曲线与拟合数据在不同Q下方差

3 回流焊接方法优化策略

根据2提出的基于常微分方程的回流焊接区域中心温度场预测模型,针对特定工业生产场景下的实际需求设计了一套回流焊接优化策略如下:①预测设定温度参数下的速度区间;②预测锡膏融化时回流面积最小参数区间;③预测锡膏融化时回流面积左右最对称参数区间;

3.1 预测设定温度参数下的速度区间

各温区温度设定条件下,利用建立的焊接区域中心温度场预测模型,对速度从小到大每隔0.1cm/min进行遍历,在所有温区温度确定、焊接中心温度曲线唯一的条件下可以找出符合表3制程界限的最大传送带过炉速度,加快工业生产速度。制程界限如下:

对于界限条件(1)、(2),要求升降温速度不超过3 ℃/s,判断是否满足

(10)

对于界限条件(3),找到150℃和190℃对应的t1和t2,判断是否满足

60≤t2-t1≤120

(11)

对于界限条件(4),找到焊锡熔点温度对应的t1和t2,判断是否满足

40≤|t2-t1|≤90

(12)

对于界限条件(5),找到f(x)的最大值Tmax,判断是否满足

240≤Tmax≤250

(13)

通过枚举速度,将焊接区域中心温度曲线T(x)离散化抽样保存到数组中,判断是否满足制程界限(10)～(13),记录速度区间并输出。

3.2 预测锡膏融化时回流面积最小参数区间

3.3 预测锡膏融化时回流面积左右最对称参数区间

各温区温度设定条件下,利用建立的焊接区域中心温度场预测模型,对速度v、各温区温度设定值TT1,TT2,TT3,TT4进行枚举,计算对应的焊接区域中心温度场变化f(x)。

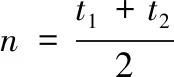
4 仿真与分析

为了证明基于区域中心温度场预测的回流焊接模型的有效性,在Matlab环境下进行仿真测试。炉内环境温度变化T(x)和某次实验中测得的焊接区域中心温度场变化f(x),如图3所示,传送带的过炉速度为70cm/min,炉温各温区温度设定如下:175℃(小温区1～5)、195℃(小温区6)、235℃(小温区7)、255℃(小温区8～9)及25℃(小温区10～11)。

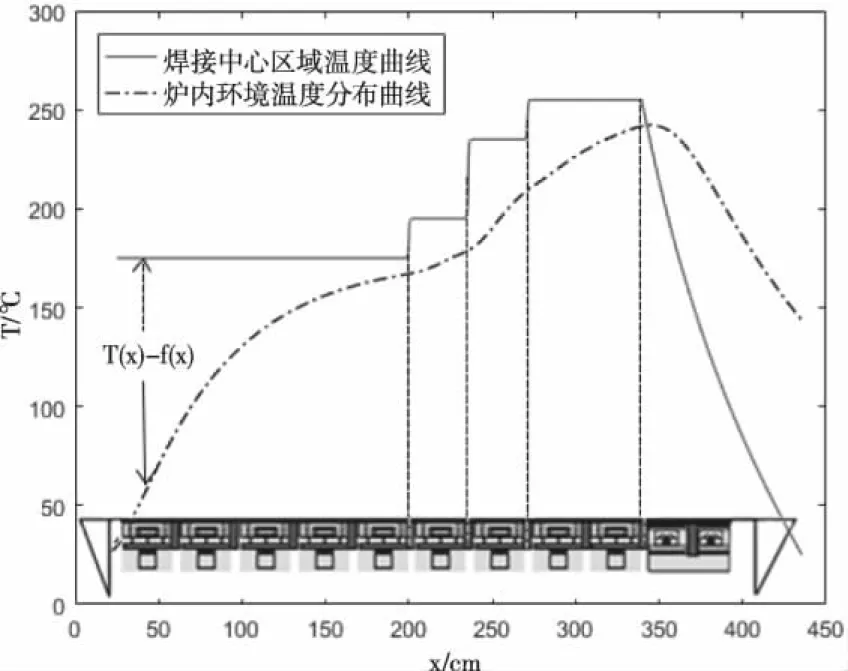
图3 炉内环境温度变化和某次实验中测得的焊接区域中心温度场变化示意图

图4为随机实验中,焊接区域中心温度曲线与不同焊接系数Q预测的对比图,发现当Q=0.021时,预测效果最佳。当最佳焊接系数Q值确定后,任意条件下的焊接区域中心的温度变化情况都可以确定。

为进一步说明本方法的可靠性,使用皮尔逊系数,由表7可知当Q=0.021时,拟合数据与真实炉温曲线高度吻合,皮尔逊系数高达99%,表现出极强的相关性,预测结果如图5所示。

表7 实际的炉温曲线与拟合出的炉温曲线在不同Q下的方差与皮尔逊相关系数

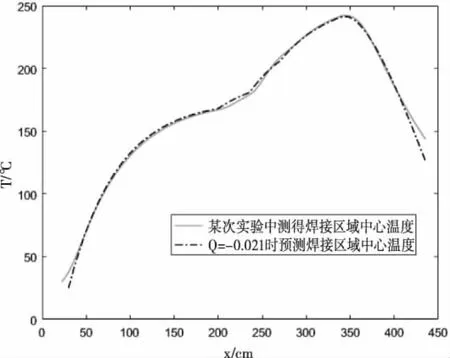
图5 某次实验焊接区域中心温度曲线与最优焊接系数Q=-0.021温度预测的对比图

5 结论

传统回流焊接工艺参数设定时多采用实验测试的方法,存在着低效、耗时、设定结果强依赖经验等问题,因此,本研究采用一种机理模型对该问题进行分析研究,提出一种回流焊接区域中心温度场预测模型,实现焊接区域中心温度场工艺参数的预测优化:根据热传导规律以及比热容公式,得到焊接区域中心温度曲线关于炉内温度分布函数在传送带位移上的一阶常微分方程,对于温差较小的间隙,使用Sigmoid函数,得到平滑的区间温度过渡曲线;对于温差较大的间隙,利用指数函数和一次函数进行线性组合,迫近实际凹函数,从而得到完整的炉内温度分布函数。通过求解常微分方程得到焊接参数,并通过计算预测温度场与真实温度分布数间的均方误差优化模型参数,得到一组符合制程界限的最优工艺参数。

同时,根据上述建立的基于区域中心温度场预测方法,针对特定工业生产场景下的实际需求设计了一套回流焊接优化策略:给定温度参数下速度区间预测策略,锡膏融化回流面积最小参数区间预测策略,锡膏融化回流面积左右最对称参数区间预测。

仿真结果表明本方法得到的区域中心温度场预测结果与实际传感器数据高度吻合,具有很强的相关性。因此,本方法可以极大的优化回流焊接生产过程,节省设备调试实践,优化生产产品焊点质量。