带场景信息的新结构Seq2Seq模型研究
2023-07-03陈其远刘源东
陈其远,刘源东,万 岩
(北京邮电大学,北京100876)
1 引言
为了解某种事物随时间变化的规律,人们通常会按照一定的频率对该事物进行观测,观测得到的结果被称为时间序列数据,对该序列的分析和处理被称作时间序列分析。时间序列分析不仅在学术上被广泛研究,同时在日常生活中有着广阔的应用领域,领域涉及气候变化[1]、生物科学[2]、制药[3]、商业市场决策[4]、金融[5]等。传统的时间序列分析模型有AR模型、MR模型、ARMR模型、ARIMA模型、支持向量机、随机森林等,但是这些模型的应用高度依赖熟悉领域知识的专家,且这些模型难以建模复杂的时间序列结构。此外,传统的模型主要适用单变量时间序列分析,比如建模某产品的销量变化。如果要建模多变量时间序列,如某连锁店的不同店铺的销量变化,则每家连锁店铺要单独建模,这不仅额外增加了计算量,还没有利用不同店铺的销量之间的关系,有可能不同店铺都存在一致的季度销量变化趋势,也可能存在两家店铺销量有跨数量级的差异。
近年来,深度学习模型在计算机视觉、自然语言处理、推荐系统等都有着广泛的应用。与传统建模方法相比,深度学习模型能从大量数据样本中自动学习到复杂的数据特征,而不需要熟悉领域知识专家的人工辅助构建特征,因此在多个领域都取得了不错的结果。现阶段有很多用经典结构的深度学习模型建模时间序列的研究,如全连接神经网络、卷积神经网络(CNN)[7,8]、长短时记忆网络(LSTM)[9,10]等,有关于如何将时间序列的领域知识结合到深度学习模型的研究[11,12]。和传统方法相比,这些方法不仅能只训练1个模型来建模多变量时间序列,还能根据近期获取的新数据微调模型,而不需要重新训练。
序列到序列(Seq2Seq)模型[13]是其中一种深度学习模型,是由编码器(Encoder)模块和解码器(Decoder)模块组成。目前已有许多研究是将经典的Seq2Seq模型直接用于时间序列分析[6,16-20]。
为进一步提升Seq2Seq模型拟合复杂时间序列的效果,本文在经典的Seq2Seq模型结构上提出了三项改进:
1)一种将外部知识引入Seq2Seq模型的方法;
2)一种由两个LSTM组成Decoder的Seq2Seq模型,该模型和经典的Seq2Seq模型比有更强的学习能力;
3)一种利用多任务学习来提升Seq2Seq模型拟合精度的方法,该方法适合拟合存在较大数量级变化的时间序列。
在某企业对企业服务(B2B服务)的成交总额(GMV)数据集(下文简称"GMV数据集")上,这三项改进的有效性通过实验得到验证。该数据集是多变量时间序列,不同企业对该B2B服务的GMV存在跨量级的差别,且GMV受包括重大节假日、所在周期的工作日天数、季节等因素的影响很大,因此该数据集对于复杂的时间序列分析任务有代表性。实验结果表明,这三项改进都能提升模型拟合的效果,且同时使用三项改进的效果比只用其中一项更好。
和之前许多直接使用经典深度学习模型结构的工作相比,本文提出了三项针对经典Seq2Seq模型结构上的改进,且这三项改进可以应用在之前采用经典Seq2Seq模型的方案上,有可能能进一步提升这些方案的效果。
2 相关理论介绍
2.1 LSTM模型
文献[15]提出了LSTM模型,LSTM模型是经典的Seq2Seq模型的构成单元。该模型能避免长期依赖问题,可以建模较长的时间序列。LSTM的结构如图1所示。由图1可知,LSTM模型是链式结构,由一系列相同的单元组成。每个单元包括Input Gate(it)、Forget Gate(ft)、Output Gate(ot)和Memory Cell(Ct)组成,其中Input Gate、Output Gate和Forget Gate能控制Memory Cell的读、写和丢失,3个控制门Input Gate、Output Gate和Forget Gate的输出分别连接到一个乘法单元上,从而实现控制功能。利用形式化语言,LSTM可以表述为

图1 LSTM单元的结构图
ft=σ(Wf[ht-1,xt]+bf)
(1)
it=σ(Wi[ht-1,xt]+bi)
(2)
ot=σ(Wo[ht-1,xt]+bo)
(3)
Ct=ft⊙Ct-1+it⊙tanh(WC[ht-1,xt]+bC)
(4)
ht=ot⊙tanh(ft*Ct-1+it⊙tanh(WC[ht-1,xt]+bC))
(5)
其中σ是激活函数sigmoid,⊙是点乘运算,W*是系数矩阵,b*是偏置向量,it、ft、ot分别表示t时刻Input Gate、Forget Gate和Output Gate的值,Ct表示t时刻Memory Cell的值,ht表示t时刻LSTM的单元的输出。
在本文,一个LSTM单元可以用图2表示,其中X表示单元的输入,Y表示单元的输出,W*表示该单元的内部参数,使用不同的W*表示不同的LSTM单元。

图2 简化表示LSTM单元
2.2 同构Seq2Seq模型
文献[8]提出了经典的Seq2Seq模型,该模型在机器翻译数据集WMT-14上取得了比只用LSTM模型更好的结果。Seq2Seq模型由Encoder和Decoder组成,Encoder和Decoder是2个独立的LSTM模型。Encoder的输入是原序列,输出了整个序列的表征向量(LSTM的最后一个单元的输出和Memory Cell的值);该表征向量是Decoder的输入,输出是目标序列。为与本文第3.2节提出的新结构Seq2Seq模型区分,经典的Seq2Seq模型在下文简称为“同构Seq2Seq模型”。
图3展示的是同构Seq2Seq模型的训练阶段。在该阶段,原序列“A、B、C”被输入到Encoder中进行编码,编码结果被输入到Decoder;Decoder在接收到编码结果后首先被输入特殊标签“

图3 同构Seq2Seq模型的训练阶段
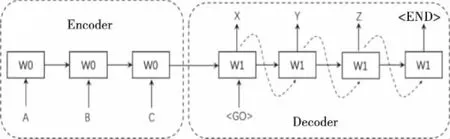
图4 同构Seq2Seq模型的预测阶段
在直接用同构Seq2Seq模型解决时间序列分析问题的方案[6,16-20]中,Encoder输入的是在一个时间点前的一段时间的序列的值,Decoder输出的是预测未来一段时间的序列的值。模型按照经典的Seq2Seq模型的方式训练和预测。其中,文献[6]在天津港进出口集装箱数据集上通过实验验证了同构Seq2Seq模型解决时间序列分析问题的效果优于传统的时间序列分析模型及其它现有的深度学习模型。
3 同构Seq2Seq模型的改进
3.1 引入外部知识
本文提出可以在同构Seq2Seq模型上添加场景信息和其它特征信息,并且把离散值输入输出序列换成连续值输入输出序列,训练、预测的方法和其它结构保持不变,新模型可用于拟合连续值时间序列并预测未来的序列的值。考虑到在有些场景任务(如给B2B服务的成交额做时间序列分析)中,节假日、所在地、季节特征等场景信息,和公司所属行业、公司规模、使用习惯等其它特征信息是可获取的,引入可知道的外部知识可能可以提升模型效果。
图5是引入外部知识的Seq2Seq模型的训练阶段,图6是引入外部知识的Seq2Seq模型的预测阶段。由图5可知,在训练阶段,Encoder的每个输入向量都是由序列的值、向量化的场景信息,和向量化的其它特征信息拼接成的;而除了在第1次解码时Decoder的输入向量是由默认值和向量化的场景信息拼接成,之后的每次输入都是由真实的序列的值和向量化的场景信息拼接而成。由图6可知,在预测阶段,Encoder的每个输入向量都是由序列的值、向量化的场景信息,和向量化的其它特征信息拼接成的;而除了在第1次解码时Decoder的输入向量是由默认值和向量化的场景信息拼接成,之后的每次输入都是由前一步的输出值和向量化的场景信息拼接而成。序列的值、向量化的场景信息和其它特征信息的描述和取值见表1。

表1 数据集的字段

图5 引入外部知识的同构Seq2Seq模型的学习阶段

图6 引入外部知识的同构Seq2Seq模型的预测阶段
3.2 异构Seq2Seq模型
在同构Seq2Seq模型中,当Encoder的编码结果(LSTM的最后一个单元的输出和Memory Cell的值)被输入到Decoder中时,Decoder在第1次解码时没有序列的值作为输入,所以将特殊标签“
图7是异构Seq2Seq模型的训练阶段,图8是异构Seq2Seq模型的预测阶段。其中,Encoder和Decoder的每一步的输入向量和同构Seq2Seq模型一致。由图7可知,在训练阶段,原序列“A、B、C”被输入到Encoder中进行编码,编码结果被输入到Decoder;Decoder在接收到编码结果后,首先将特殊标签“
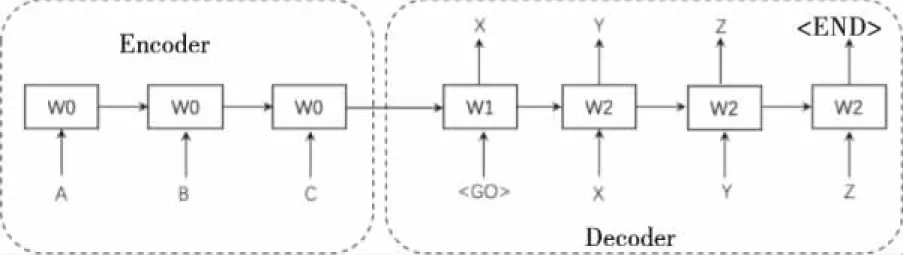
图7 异构Seq2Seq模型的学习阶段
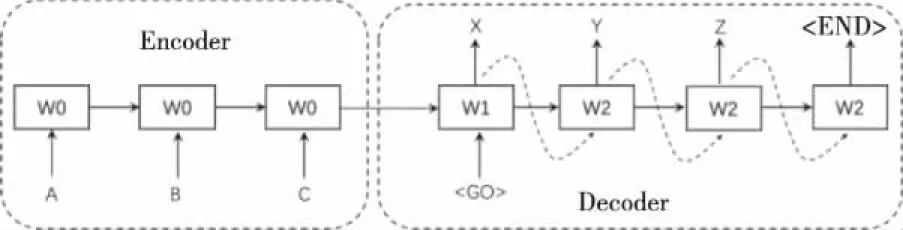
图8 异构Seq2Seq模型的预测阶段
3.3 利用多任务学习来提升同构Seq2Seq模型拟合存在较大数量级变化的时间序列的精度
预测时间序列的值中,有可能出现少数序列的值的预测结果和真实值有不少于2个数量级的误差的情况。为解决该问题,本论文提出的方法是将Decoder的输出分成量级部分和除数部分。例如,待预测值是349.3,可以被拆成100×3.493,级数用3位One-Hot编码表示成“100”(称作“量级向量”),有效数除以10成0.34903(称作“除数向量”,除以10以确保除数部分在[0,1)之间)。
新方法的Decoder单元结构如图11所示。和图1所示的结构相比,该单元的输入由量级向量nt-1和除数向量at-1拼接而成,输出向量ht分别接2个全连接网络,一个输出量级向量nt,另一个输出除数向量at。量级向量是One-Hot向量,除数向量是维度是1×1的向量。损失函数的公式如下

(6)

图9是在同构Seq2Seq模型上采用新方法后的学习阶段,图10是在同构Seq2Seq模型上采用新方法后的预测阶段,其中W、X、Y、Z是预测结果的除数部分。由图可知,学习阶段和预测阶段的Encoder和同构Seq2Seq模型一致,而学习阶段和预测阶段的Decoder单元的结构如图11所示。在训练阶段,Decoder的输入是由真实的序列的值计算得到的量级向量和除数向量;在预测阶段,除第1次解码输入的是特殊标签“

图9 利用多任务学习提升拟合精度的同构Seq2Seq模型的学习阶段

图10 利用多任务学习提升拟合精度的同构Seq2Seq模型的预测阶段

图11 利用多任务学习提升拟合精度的同构Seq2Seq模型的Decoder单元
4 模型评估
4.1 实验数据集
为了验证所提出方法的有效性,本文选取了某B2B服务的每日成交总额作为原始数据,并以每28日为滑动窗口求和制作每28日成交总额数据集。数据集的字段如表1所示。数据集的起始日期是2018年1月1日,结束日期是2021年3月30日,共有8000家企业。
4.2 数据预处理
数据预处理的流程是首先过滤无效数据,然后用滑动窗口划分数据集,最后对数据进行归一化。
1)过滤无效数据
在2020年3月30日之前没有使用过该B2B服务超过252天(9个28天)的企业,即在2020年9月12日前的成交总额都是0的企业,需要在预处理阶段被过滤掉,因为开始使用该B2B服务到截止的日数的天数小于滑动窗口的长度。这样的企业有51家。
2)通过滑动窗口划分数据集
实验采取滑动窗口的形式来制作训练集、验证集和测试集,将每252天(6个28天作为输入,3个28天的最后1天作为输出)作为一个时间窗口,并按天滑动。
3)归一化
不同信息,如公司规模、统计周期工作日天数、成交额、订单量等,取值可能相差很大。为保证模型能稳定收敛,在预处理阶段要对这些信息作归一化。这里采用等频分箱归一化[14]。等频分箱归一化能很好地保留数值之间的区分度,并且增强了模型对异常值的容错能力。在对数据归一化后,模型的输出结果也是归一化后的预测结果,因此归一化阶段的映射关系要保留,并将归一化后的预测结果还原成真实的值。
4.3 评价指标
本文比较了不同改进方法对Seq2Seq模型效果的提升,评价指标是平均绝对误差(Mean Absolute Eror,MAE)和绝对百分比误差(Mean Absolute Percentage Error,MAPE),评价指标的具体公式如下

(7)
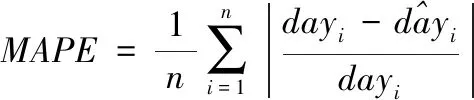
(8)
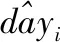
4.4 实验平台
实验的模型是在Tensorflow 1.14上搭建的,CPU型号是Intel(R)Xeon(R)CPU E5-2630 v4 @ 2.20GHz,内存有251.671875GB,GPU型号是NVIDIA Tesla P40。
4.5 模型的超参数
模型采用批量梯度下降(BGD),epoch是8,batch_size是1024,优化器是自适应矩估计(Adam)[15],优化器参数参数是0.0005。模型每次输入6个连续的28天的每28天B2B服务的成交总额,模型的Memory Cell的维度是96。
4.6 实验结果
实验比较了同构Seq2Seq模型、引入外部知识的同构Seq2Seq模型、异构Seq2Seq模型、通过多任务学习提升精度的同构Seq2Seq模型、同时有3项改进的Seq2Seq模型,实验结果如表2所示。

表2 实验结果
从表2可以看出,本文提出的3项改进都可以有效提高预测精度,且同时使用3项改进的效果最好。和同构Seq2Seq模型相比,单独使用1种方式能将MAE降低12.83%~39.54%,MAPE降低4.76%~15.87%;同时使用所有方法能将MAE降低47.55%,MAPE降低25.40%。
5 结束语
本文提出了3项对经典的Seq2Seq模型结构的改进,经实验验证,上述改进可提升Seq2Seq模型拟合复杂时间序列的效果,改进后MAE最多可降低47.55%,MAPE最多可降低25.40%。
在未来的研究中,将考虑引入注意力机制,并将这三项改进应用在已有的直接用经典Seq2Seq模型解决时间序列分析问题的方案上,从而测试这三项改进的效果。
