计算机视觉技术的位姿估计处理方法

2023-07-03孟建军陈晓彤李德仓祁文哲

计算机仿真 2023年5期

孟建军,陈晓彤,李德仓,祁文哲

(1. 兰州交通大学机电技术研究所,甘肃兰州,730070;2. 甘肃省物流及运输装备信息化工程技术研究中心,甘肃兰州,730070;3. 甘肃省物流与运输装备行业技术中心,甘肃兰州,730070)

1 引言

智能化和信息化技术的应用在很大程度上解放了人们的双手,减少劳动力的投入,节省了企业的人工成本且保障了人身安全。因此,工程领域智能化与信息化的发展有助于自动化模式的形成,加快社会经济发展进程[1]。

采用视觉技术从周围环境图像中提取有用的信息,并恢复场景的三维图像,从而确定目标、识别路径、判断沿途是否存在障碍物,最终得到可行驶范围和障碍规避[2.3]。在陌生环境或者是GPS(Global Positioning System)定位无法发挥功效的情况下,便需要实现自身的实时准确定位和当下环境的建图。目前,较为热门的同步定位与建图(Simultaneous Localization and Mapping,SLAM)主要依赖激光雷达传感器和视觉传感器来帮助其完成一系列动作指令。SLAM算法是一种实现定位并进行地图构建的系统。而ROS机器人系统(Robot Operating System)则可以提供环境感知、运动控制、路径规划等研究领域经典并且前沿的算法代码库,可以加强机器人代码的复用率的模块化[4]。

为了实现机器人自主导航作业,许多智能算法被大量应用。为提高作业的准确性,这就要求准确掌握环境中的物体姿态,从场景图像中确定目标图像位姿的问题核心就是位姿估计。近年来,位姿估计逐步成为计算机视觉研究的研究热点。Sarlin[5]等人提出了层次定位方法,上述方法利用卷积神经网络在场景图像中找到候选帧,候选帧聚类后与查询图像进行特征点匹配,建立特征点的2D-3D对应关系,使用PnP算法估计相机位姿;Chen等[6]使用热力图表示方法回归目标稀疏关键点,使用模拟退火算法筛选外点,并设计非线性优化方法求解PnP问题,上述方法均利用PnP算法处理位姿问题,但存在一缺陷,若噪声影响3D点或2D点,易发生错误匹配问题。EPEL＿cvlab[7]将图像均匀分割成若干网格,借助图像分割的方式预测卫星的8个三维包围框角点,使用EPnP求解位姿,EPnP算法在深度范围变化大的环境下求解位姿精度明显降低。这些算法虽然在性能上取得了一定的优越性,但仍然存在不足,例如存在归纳偏置问题,从而导致训练所得到的模型泛化能力不足;存在缺少绝对位置信息、建模能力不足等;其中传统ICP算法(Iterative Closest Point迭代最近点),首先要将边界点以及深度过大的点剔除,然后进行点云之间的匹配,并未包含局部坐标信息,最后通过多次迭代搜索最近点,这会造成高额的计算代价,且对深度未知的点无法计算;而EPnP(Efficient Perspective-n-Point)算法精度较高、能很好地解决图像深度和抗干扰能力差的问题,但是存在模型泛化能力不足等缺陷,分析ICP算法和EPnP算法缺点,结合二者的优点。因此,提出一种将ICP和EPnP结合的算法,用于计算机视觉图像处理的位姿估计,在实时性和准确性上有较大提高。

2 算法框架设计

对环境物体定位,主要是通过设定一个形状特别又易辨识的标杆,利用相机对环境中的物体进行获取,提取特征点,并对图像中的特征点坐标处理,之后再提取其像素坐标,进行比对筛选剔除;接着求解相机的位姿状态,提高定位精度;最后对图像中物体姿态进行位姿估计,算法框架如图1所示。

图1 算法框架

3 位姿估计算法

3.1 ICP算法

ICP配准法主要用于解决基于自由形态曲面的匹配问题,其特点在于在进行算法匹配的过程中不需要进行环境特征的提取,并且收敛速度和匹配精度完全依赖于相匹配的两个点云数据中最邻近点对的搜索结果。目前,最邻近点对的搜索方式主要有:点到点最邻近搜索、点到平面最邻近搜索算法、点到投影、收缩投影点最邻近搜索[8]。

传统的ICP算法是一种点集之间的配准方法。通过相机坐标系获得图像特征点的坐标值,然后利用奇异值分解或最小二乘法进行位姿的求解,最终得到旋转矩阵和平移矩阵,如式(1)和式(2)所示。

(1)

(2)

(3)

3.2 EPnP算法

PnP(Perspective-n-Point)是在世界坐标系下给定一组由n个3D点组成的点集,将点集在图像中投影出相应的2D图像,以此解决相机的位姿问题。通过6个自由度组成的相机位姿包括旋转和相机对于世界的平移,其中旋转包括滚动、俯仰以及偏航。位姿估计问题的关键在于相机校准,而且广泛应用于计算机视觉和其他领域中,如机器人等[9]。

(4)

(5)

(6)

(7)

当四个控制点和图像点对应时,将n个参考点带入式(7),就会产生一个线性方程组,即为:Mx=0,式中x是待求的12个未知数,M为2n*12的矩阵,如式(8)所示。

(8)

根据欧氏变换,将已知的四个控制点间距转换为四个点在相机坐标系下的坐标,从而将图像从三维变换为二维进行求解。

3.3 ICP和EPnP混合算法

EPnP算法将参考点的坐标表示为控制点坐标的加权和,如式(9)所示。

(9)

根据ICP的代数求解方法,找出第i个点的误差项,表示如式(10)所示。

(10)

然后建立最小二乘问题,利用奇异值分解(SVD)的方法求解最小的误差平方和。鉴于深度图像有噪声影响,可能存在数据丢失的问题,因此采用混合使用ICP和EPnP的算法,对于已知特征点,采用ICP算法的运动恢复方法,对于未知特征点使用EPnP算法的运动恢复方法。并利用三维线性空间内4个控制点组成的基来重新表示三维空间,然后求解将n个空间点转化为相机坐标系下的坐标问题,最终得到一个线性方程。上述方程的解位于矩阵M的零空间,则有式(11)所示。

(11)

式中:vi(i=1,2,…,N)表示矩阵MTM所得特征值对应的特征向量,βi是第i项化简后的系数。由此得到,在相机坐标系下的4个世界坐标系控制点坐标,进而得到n个世界坐标系下参考点在相机坐标系下的坐标。最后,将转化为已知世界坐标系下的3D点到相机坐标系下3D点的对应关系来求解相机位姿的问题,同样由SVD来进行求解[11]。

4 结果与分析

4.1 实验平台搭建

所有算法的实现均采用的是MATLAB 软件进行仿真实验。其中所涉及的数据为随机数据,避免了仿真数据结果的偶然性。

4.2 ICP算法结果

对插入的数据模拟一个三维图像,分别从x、y、z三个方向拆分图像,如图2所示,其中图2(a)是x轴方向图像,图2(b)是y轴方向图像,图2(c)是z轴方向图像。可发现拆分图像中存在或多或少的噪音且为未知特征点。

图2 原始数据三个方向拆分图像

图3是ICP算法处理结果图比对图,其中图3(a)是原始图像,图3(b)是处理结果。图3(a)与图3(b)对比发现存在一定的误差,且在配准精度和效率上存在差异,在处理过程中就近搜索相应的就近点,计算点集的重心位置,然后生成新的点集,提供正定矩阵及其特征值和最大特征向量,在旋转矩阵的确定下发生平移。在原始数据深度过大或者噪声影响过大的情况下会产生误差,从图3(b)中可以清楚看出数据点发生的偏移。

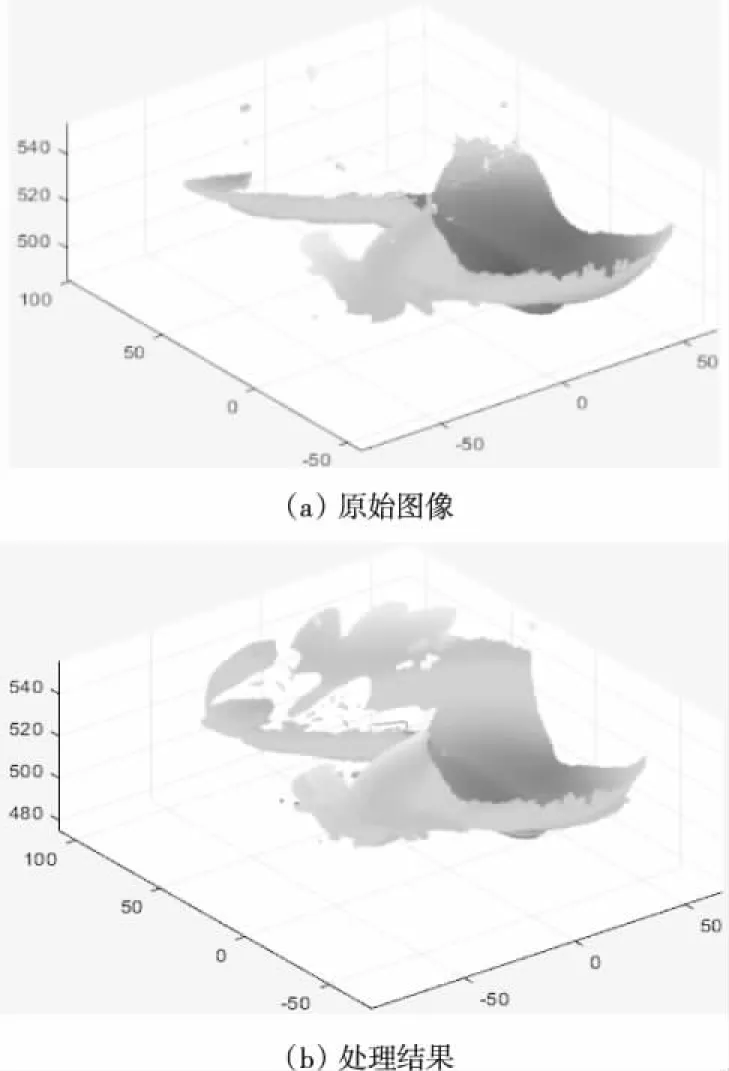
图3 ICP算法处理结果比对图

4.3 EPnP算法结果

EPnP算法主要是处理空间中点对于深度的影响的拟合关系,因此,本节利用随机产生100个数据点和噪声设置为20,进行图像仿真,图4是原始数据与噪音图,采用MATLAB进行仿真实验,图中的圈代表了噪音,点代表数据点位置。

图4 原始数据与噪音图

图5是EPnP算法处理结果图,通过图像中的红点和蓝圈的位置关系和图4中的红点和绿圈的位置关系比对,可以发现在很大程度上二者发生重合。由此可见,EPnP算法可以有效地减少噪音对位置点的影响。

图5 EPnP算法处理结果图

4.4 ICP和EPnP混合算法结果

基于EPnP算法处理后的效果和ICP算法处理后存在的问题,结合二者优点,采用 ICP和EPnP混合算法。因此,在融入EPnP算法后,选择4个控制点,同时对这4个控制点进行优化,所以加快了运算速度;在式(8)中,只需考虑4个奇异向量,提高了识别精度。

对于已知特征点,采用ICP算法的运动恢复方法,对于未知特征点使用EPnP算法的运动恢复方法。利用三维线性空间中的基底来重新标定三维空间的点,然后求解图像中n个特征点在相机坐标系下的坐标,最后求解相机位姿问题。通过融合EPnP算法便弥补了ICP算法处理过程由于深度和噪声而产生的误差影响。理论上所处理的效果图为如图6。相对比下会发现,改进后的算法所受到的深度影响较小,与原图的相似度更高。

图6 ICP和EPnP混合算法处理结果图

4.5 结果对比及分析

ICP算法是传统的位姿估计算法,通过对比图3中a、b两图,可以直观地发现图像在上方存在一定的误差,而其余部分图像相似度很高,由此可知在特征点已知的情况下,ICP算法可以很好地进行仿真估计,但在点云特征点未知的情况下,就存在数据的偏移而引起图像的失真问题。EPnP算法侧重点在于点云特征点未知的问题上有很好的解决方法,针对图4和图5中的噪音和特征点重合程度的对比,可看出EPnP算法有效地解决了噪声影响问题,更好地进行点云与点云之间的拟合。因此,ICP和EPnP混合算法是综合了二者各自的优点,通过图6与图3(b)对比,可以发现图像上侧在图3(b)中的失真问题在图6中有所减少,有效解决了ICP算法中存在的较为严重的噪音问题,可以提高图像位姿的准确度。