极化码在水声通信系统中的应用研究

侯卫民,魏泽强,胡金霞,苏 佳

(河北科技大学信息科学与工程学院,河北 石家庄050018)

1 引言

随着海洋开发的日益增加,水声通信技术的发展备受关注。水声通信的传输媒介为水声信道,水声信道的时变效应、多径效应以及来自多方面的噪声和有限带宽等特点大大制约了水声通信技术的发展[1]。为了改善水声信道对信号传输的影响,很多技术手段例如信道编码和OFDM技术等常应用在水声通信系统中。传统的信道编码方案例如里德-所罗门(Reed-Solomon, RS)码、卷积码常应用在早期水声通信系统中[2],信道编码技术的引进如卷积码等方案很大程度提升了水声通信系统的可靠性。随着水声通信技术的发展,Turbo码[3]与低密度校验(Low Density Parity Check, LDPC)码[4]在水声信道中被证明有良好的纠错性能,也逐渐应用到了水声通信系统中。Turbo码与LDPC码两种编码虽能够有效提高水声通信系统可靠性,但两者在理论上都并未达到香农限。当前先进的信道编码技术与水声通信相结合成为一个新的发展趋势。极化码在2009年被提出后,首次证明在二进制对称信道下可以达到香农限[5],其编解码也有较低的复杂度。目前极化码作为信道编码方案已经成为5G技术标准之一,成为相关领域研究热点。而水声通信系统中另一个常应用的OFDM技术能够有效的对抗多径效应带来的频率选择性衰落,OFDM技术还因频带利用率高等原因应用场景广泛,因此将极化码作为信道编码方案并结合OFDM技术应用到水声通信系统中,整体水声通信系统框图如图1。

图1 水声通信系统框图

在发射端,由信息源产生的随机0、1序列先通过极化码编码来提高可靠性后,接着对编码后比特进行调制,之后将信号转化为并行信号并加入导频,对信号进行IFFT运算并加入循环前缀,循环前缀可以消除符号间干扰,最后将信号转换成串行信号发送到水声信道中。在接收端处,进行相应逆操作,进行FFT运算后,根据之前加入的导频进行信道估计与信道均衡操作,最后相应解调、解码,最终接收到原始二进制信息序列。

整体水声通信系统中侧重研究极化码在系统中的性能表现,极化码是线性分组码,其编解码是基于信道极化原理,信道极化包括信道合并与信道分裂。信道极化后,子信道的信道容量呈两极分化,如何挑选信道容量大的子信道传输信息称之为极化码的构造问题,不同的信道类型往往有着不同的构造方法。Arikan教授提出在二元删除信道(Binary Erasure Channel,BEC)下,可以通过巴氏参数法来计算每个信道的巴氏参数。在二元对称信道(Binary Symmetrical Channel,BSC)下,Mori等学者提出了密度进化法(Density Evolution,DE)[6]。针对高斯信道的构造方法还有高斯近似法(Gaussian Approximation, GA)[7]。

全文安排如下:在第二节研究极化码的基础理论,在第三节主要对水声信道进行分析,最后在第四节研究极化码在水声信道中的性能表现。

2 极化码原理基础

2.1 信道的可靠性度量

信道W的特性常用信道互信息I(W)和巴氏参数Z(W)来表示。在对称信道下,互信息I(W)等于信道容量。Z(W)表示子信道的可靠程度。一般地,I(W)与Z(W)呈反比关系,Z(W)越小,则代表该信道传输可靠性越好,信道容量就越高,反之则可靠性越差,越不利于传输信息[9],其中

(1)

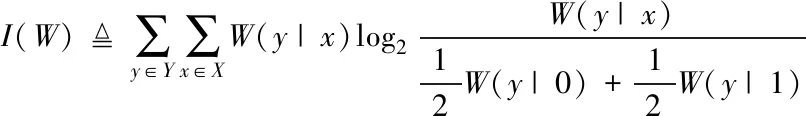
(2)

2.2 信道极化原理

信道极化由信道组合和信道分裂组成。信道组合是将N条信道特性相同的子信道以递归的方式合并成一个信道,而信道分裂则是将组合好的一条信道分裂成N条子信道。信道极化后,总信道容量不变,其中一部分子信道信道容量趋于1,称为无噪信道,用来传输信息比特,另一部分的子信道的信道容量则趋近于0,称为纯噪声信道,用来传输通信双方已知的冻结比特,称为信道极化现象。N越大,信道容量趋于1的比例就越大,信道极化现象越明显。以BEC信道为例,图2为N=1024的信道极化图。

图2 信道极化图

2.3 极化码编码

极化码的编解码是基于信道极化现象的,在编码前需要对每个子信道进行可靠性估计,信道类型不同,构造方法不同。以针对BEC信道的巴氏参数法为例,直接计算每个子信道的巴氏参数,将巴氏参数按照由低到高进行排序,巴氏参数低的传输信息比特,高的传输冻结比特。子信道的巴氏参数计算如下

(3)

(4)

其中式(3)当信道为BEC信道时取等号。

信道可靠性度量完成后,进行极化码编码,用式(5)来表示

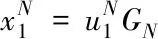
(5)

其中N为码长,u1为信源比特,x1为编码后的比特,GN为生成矩阵

GN=BNF⊗n

(6)

BN也称为比特置换操作

BN=RN(I2⊗BN/2)

(7)

F为核心矩阵,⊗称为克罗内克积。

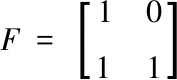
(8)

2.4 极化码解码

极化码解码算法通常有串行抵消(Successive Cancellation, SC)解码算法、置信传播(Belief Propagation, BP)算法以及串行抵消列表(Successive-Cancellation List, SCL)算法[10,11]和软输出连续删除(Soft Cancellation, SCAN)算法。

由于SC解码为串行解码,采用逐个比特译码的方式,各个解码判决结果相互关联,一个比特错误判决可能影响后面的判决。一般SCL解码性能在极化码解码算法中为较好的,但SCL解码随着搜索宽度的增加,复杂度也会相应的增加。BP解码为并行解码,相较于SC解码具有延时低、吞吐量大等优势,所以选择BP解码算法为主要研究对象。BP解码原理为:

BP解码算法是通过对因子图进行左右迭代来完成的,因子图一共由N(n+1)个节点组成,图3描述了n=3,N=8时的极化码解码因子图。

图3 整体BP解码图

由图3可以看出当码长为8时,BP解码算法分为三个阶段,其因子图中的基础运算单元如图4。

图4 基础运算单元

在因子图中,信息先从最右端开始更新,更新到最左端后,再更新到最右端完成一次迭代。在每轮迭代中,信息都是以对数似然比(Log-Likelihood Ratio,LLR)形式在因子图中传递。整体解码流程为:

1)信息的初始化;

因子图中最左端信源比特的LLR信息

(9)

再计算来自接收端的LLR信息

(10)

2)根据下列迭代公式更新因子图中节点的LLR信息;

(11)

(12)

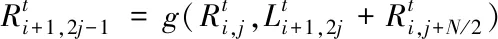
(13)

(14)

迭代公式中g(x)为

(15)

3)判决

当BP解码达到最大迭代次数时,进行判决,判决方式如下

(16)

3 水声信道与极化码

本节主要对水声信道进行分析,并研究极化码在水声信道中的编码机制。

3.1 时变信道模型

信号在水声信道传播时,若发射机与接收机存在相对运动,则会出现多普勒效应,信号传播路径发生改变,多径信号到达接收端的时间和入射角也随之改变。水声信道的时变特性主要是基于多普勒频移产生的。

水声时变信道模型可以表示为

(17)

其中,L为信号传播的总路径数,fl为多普勒频移。信道h(t,τ)共有L条路径,第l条路径的幅度为hl(n),时延为τl。

本文中水声信道模型各径的具体时延、幅度数据是通过BELLHOP模型获得,BELLHOP模型为射线声学模型,可以通过配置相应水体环境来输出水声信道信息[12],一般时变信道模型适合浅海复杂的通信环境,水体环境配置见表1。

表1 环境配置参数

设置相应水体环境后,BELLHOP会输出与水体环境所匹配的文件,根据输出文件可以得到水声信道的一些基本特征,由仿真中得到水声信道某一时刻的声线传播图、水声信道的归一化冲激响应,分别如图5、6。

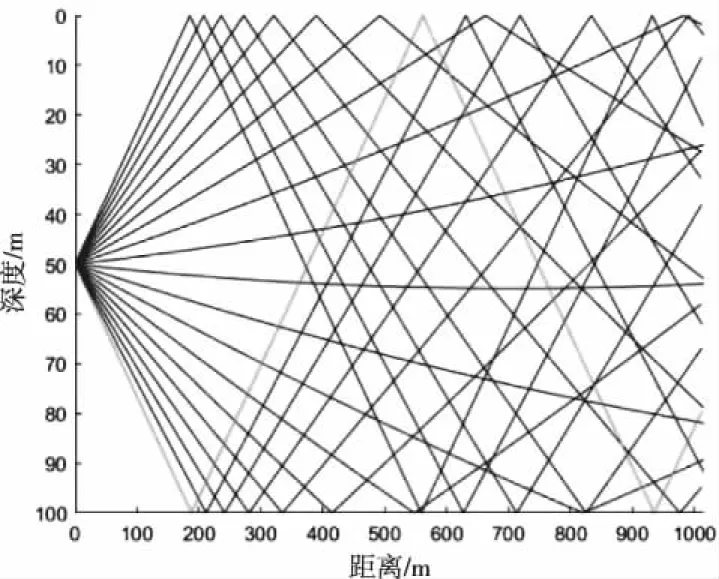
图5 浅海声线传播图

由图5分析总体水深100m,发射机与接收机都位于水深50m处,信号传播路径总共为20条,经过海面和海底的反射和折射达到接受端,通信距离为1000m。

由图6可以看出20条路径的相对时延以及相对幅度,相对时延主要分布在0ms到15ms之间。

图6 水声信道归一化冲激响应

通过BELLHOP模型仿真水声时变信道模型给出时变信道仿真参数见表2。

表2 时变信道仿真参数

给出各径的相对时延和相对幅度后,在时变水声信道模型中引入一个变量,归一化最大多普勒频偏(Normalized Maximum Doppler Frequency Shift,NMDFS)ε。它表示为最大多普勒频偏fdmax与载波间隔Δf之比,即ε=fdmax/Δf。然后给出表3时变信道下fdmax和归一化频偏ε的值。

表3 仿真参数

3.2 时不变水声信道模型

时不变信道模型,指的是各径衰落系数以及时延不随时间变化而变化,也被称为确定性水声信道。一般适合于较为稳定的水下环境。该模型的冲激响应可以表示为

(18)

其中L为总的路径数,hl为第l径的加权系数,τ为时延。

相同地,通过BELLHOP模型配置深海较为稳定的水体通信环境来仿真水声时不变信道模型[13],仿真参数见表4。

表4 时不变信道仿真参数

3.3 极化码在水声信道中的构造

极化码在水声信道中的构造采用巴氏参数边界法。由2.2节式(3)和式(4)知巴氏参数的计算,在水声信道中用式(19)来代替式(3)来更新巴氏参数。

(19)

由式(1)可知巴氏参数需要计算信道转移概率,水声通信模型在频域中一般表示为

Yi(k)=Hi(k)X(k)+Wi(k)

(20)

其中,Yi(k)为接收端接收信号,Hi(k)为水声信道频率响应,X(k)为信号输入,Wi(k)为均值为0,方差为σ2的高斯白噪声。Hi(k)可以通过信道估计获得,例如LS信道估计算法等方法。Wi(k)可以通过不用信号传输来进行测量[14]。

信号经过BPSK调制后,水声信道的转移概率为

(21)

(22)

4 极化码在水声OFDM系统的仿真

4.1 OFDM仿真参数设置

OFDM水声通信系统仿真参数见表5。

表5 OFDM系统参数

4.2 极化码在时不变信道下的仿真

时不变信道仿真数据如表4。极化码的构造选择巴氏参数界法,解码算法为BP解码算法。主要从码长、多径数量、BP解码迭代次数等方面去仿真分析。

4.2.1 不同码长在水声时不变信道下的仿真

设置极化码的码长N=128,256,512,码率R=0.5,如图7。

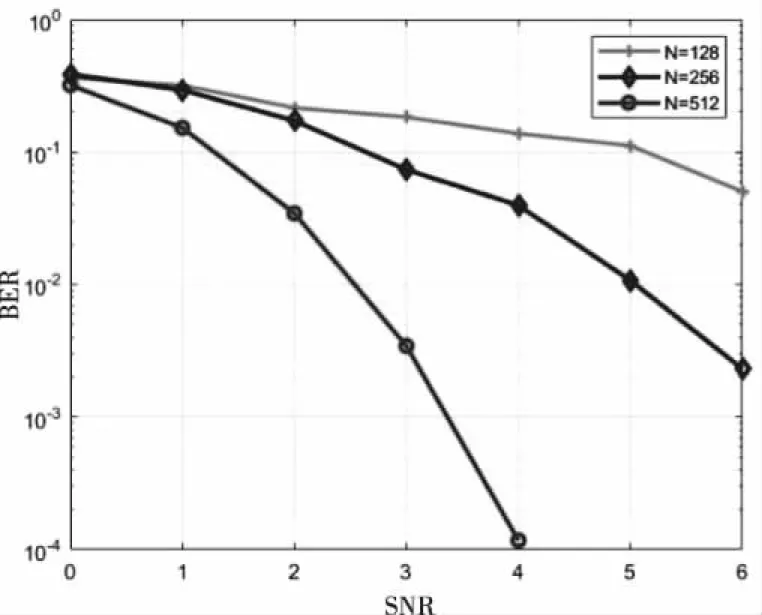
图7 不同码长的性能表现

从图7中整体看误码率会随着信噪比的增大而逐步减小,码长越长,其误码率性能越佳。极化码码长越长,其信道极化比例越大,可靠性就越高。当码长为512时,在信噪比为4dB时,误码率可以达到10-4,可以满足基本水声通信要求。

4.2.2 多径数目不同在时不变信道下的仿真

固定N=512,R=0.5,仿真信号传播的多径为1、3、5径。仿真效果如图8。

图8 不同多径数目的误码率表现

由图8分析得多径的数量越少,整体误码率性能越佳,固定误码率为10-3数量级,1径相对3径增益约1.5dB左右,相对5径约2db左右。

4.2.3 不同解码算法在时不变信道中的仿真

设置N=512,R=0.5,主要研究极化码SC、BP、SCL、SCAN四种解码算法在水声时不变信道下的性能表现。其中BP迭代次数为40,SCL解码算法搜索宽度为8,SCAN算法迭代次数为1,仿真如图9。

图9 极化码的不同解码算法仿真

由图9可以看出在极化码的解码算法中SCL算法性能好于其它解码算法,BP解码算法相较于其它解码算法性能略低,但在总体上与SC、SCAN等解码算法差距不大,且性能会随着BP迭代次数的增加逐渐增加。

4.2.4 BP解码不同迭代次数在时不变水声信道模型下的仿真

设置N=512,R=0.5,迭代次数分别为15、40、65在水声信道下仿真如图10。

图10 BP解码不同迭代次数仿真

由图10分析得极化码BP解码迭代次数越大,其误码率越低。在误码率为10-3数量级上,迭代次数65相较于迭代次数40有着0.25dB的提升。

4.3 极化码在时变信道下的仿真

时变信道仿真数据如表2。主要从码长、码率、以多普勒频移等不同参数对性能的影响,最后在时变信道下分别进行卷积码编码与极化码编码并对比。

4.3.1 不同码长在时变信道下的仿真

固定N=512,R=0.5,BP解码迭代次数为40,fdmax为0.002Hz。N=128,256,512,仿真如图11。

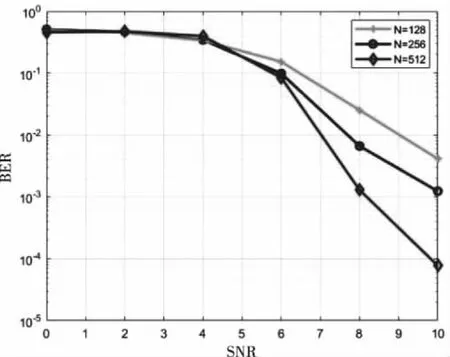
图11 时变信道不同码长仿真

由图11得出N越大,误码率越低,在信噪比较低时,不同码长误码率性能接近一致,在信噪比5dB以后,误码率随着信噪比增大开始逐步降低,直到信噪比为10dB时码长512的误码率达到10-4至10-5。

4.3.2 不同码率在时变信道下的仿真

N=512,fdmax为0.002Hz,BP解码迭代次数为40。R=0.25,0.5,0.75,仿真如图12。

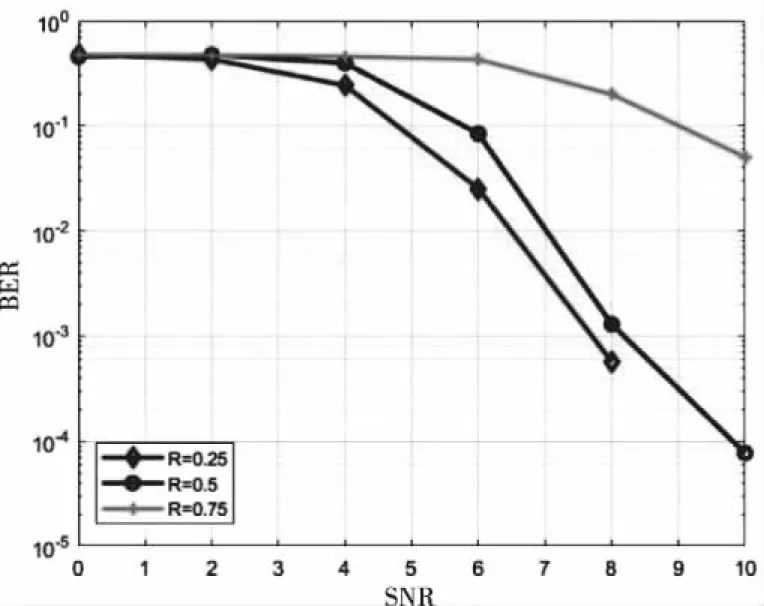
图12 不同码率仿真

由图12得出码率越小,其误码率越低,当R=0.75时,误码率基本维持在一个高的水平,原因为信息位过多,信道极化后,一部分信息位占用了信道可靠性低的子信道导致。码率0.25的误码率虽然要比码率为0.5的要略低,但通信效率太低,一般选择码率0.5进行通信。

4.3.3 不同多普勒频移在时变信道下的仿真

固定N=512,R=0.5,BP迭代次数40,fdmax为0.002,0.02,0.2,仿真如图13。

图13 不同最大多普勒频移仿真

由图13分析,当fdmax固定时,信噪比越大,其误码率越低。当信噪比固定时,fdmax越大,其误码率越高。当归一化频偏大于0.01时,极化码的性能开始降低,已经不能满足水声通信的基本要求,所以一般通信中归一化频偏要低于0.01。

4.3.4 卷积码与极化码在时变信道中的仿真对比

卷积码的约束长度为7,极化码与卷积码码长都为512,码率为0.5。仿真如图14。

图14 极化码与卷积码对比仿真

由图14可以看出随着信噪比的增加,误码率在逐步降低,极化码的BP解码算法性能最佳,固定误码率为10-3,极化码编码相对卷积码有着2dB左右的提升。

5 结论

本文首次用BELLHOP模型仿真水声信道与先进信道编码技术极化码结合,且在极化码原理基础上,验证了构造方法为巴氏参数边界法在水声信道的可行性,尤其在时不变水声信道下性能良好。另外针对水声信道,用BELLHOP模型仿真不同水声信道模型,得到传播声线图、各径的相对时延以及相对幅度等数据。在极化码解码方面,通过仿真对比各解码算法优缺点最终选择BP解码算法。最后分析了BP解码算法在不同水声信道模型、不同信道参数下的性能。仿真表明,极化码的BP解码算法可以满足基本水声通信要求,能够有效提高水声通信可靠性,且性能优于卷积码。