基于相位差异法的多帧遥感降质图像复原仿真

展金梅,祁 冰

(1. 琼台师范学院信息科学技术学院,海南 海口 571127;2. 海南大学网络空间安全学院,海南 海口 570228)

1 引言

遥感技术能够实现长距离、非接触性的探测工作,常规情况下,为使探测结果更加精准,会用无人机对同一目标进行多次采集成帧,全方面、多层次、多角度获取被测主体特征[1,2]。但是在遥感图像采集中,大气作为一种成分随机的极不稳定物质,光波可能遭受到湍流、散射以及随机分子吸收率等多个干扰[3],这会极大程度降低遥感图像质量,如:大气分子吸收能量和色散过程中都会衰减光波能量,引发细节消光或磁波偏振现象[4];受温度影响,介质分子随机运动,此时新的湍流结构又会导致折射率发生不可预测的变化,令光波振幅和相位随之起伏,出现难以有效剥离的随机噪声,这都导致遥感图像出现虚焦或图像畸变等问题[5]。另外遥感技术使用的光学成像仪器,它本身的零部件也会受到大气温度、风速、光照强度等应力变化的影响,难以使图像呈现出理想的分辨率,也会导致前相位误差[6]产生,令图像像素峰值、质量降低,像素出现漂移,阻碍人类向未知领域的探索。

为此,本文针对大气实时性变化特点以及遥感仪器零部件缺陷,提出一种遥感图像复原方法,重点凭借相位差异法来修正波前畸变。相位差异法能够反演经两次傅里叶变换后的遥感成像流程,并通过正则化约束目标函数和代价函数,避免复原结果陷入病态化问题中,最后得出正则化因子为非负数且无限趋近于0时,能够输出最优复原结果。本文方法能够在遥感成像中独立使用,既不受限于遥感仪器分辨率、零部件等硬件条件,也不约束自然环境,具有较好的适应性,能够修正大气湍流和光学系统的双重误差。

2 多帧遥感图像成像及预处理

遥感技术一般会通过多通道同时拍摄单帧或多帧的短曝光图像,在此过程中,所有像素形成均处于线性或者空间不变状态[7],大气湍流和光学系统的噪声也多为加性干扰[8],噪声和遥感目标间相互独立。多帧遥感图像模型可以表示为

Gi[δi(x,y)]=I(x,y)·Hi(x,y)+Ni(x,y)

(1)

式中,Ni(x,y)表示加性干扰噪声,Gi(x,y)表示采集的波前畸变遥感图像,δi表示第i帧遥感图像和真实观测场景的空间维度转换值,(x,y)表示图像像素,I(x,y)表示理想图像,Hi(x,y)表示图像点扩展函数。

相位差异法作为一种波前畸变修正法,虽可以处理较为隐蔽的随机噪声和加性噪声,若图像内存在明显干扰,该方法的收敛性就会降低,为此,本文先通过自适应滤波进行调整,首先剔除明显的高频干扰,令后续迭代速度加快。

本文使用的是Butter worth低通滤波器,其优势在于通带与阻带之间没有明显的起伏变化,二者间的平稳过渡带能降低多帧图像处理后目标间的不连续性,且经过滤波后,遥感对象的边缘特征不会过度平滑[9],还能避免振铃现象发生[10],在去除突出干扰的同时,最大程度降低图像模糊化程度,方便后续对图像的恢复工作。

将理想环境下的遥感成像系统传递函数,代入到Butter worth低通滤波器中设置合理参数,滤波器滤波可表示为

(2)

式中,ω表示传递函数OTF的截止频率,且ω∈[0,1]区间,c表示多帧光学成像的梯度方向,n表示滤波器阶数。

考虑实际遥感成像过程,进一步进行归一化处理

(3)

式中,MTF表示遥感成像系统的整体截止频率,满足

MTF=MTFoptic·MTFccd

(4)

式中,MTFoptic表示遥感成像系统理论上的截止频率,MTFccd表示拍摄CCD相机的截止频率,MTF、MTFoptic、MTFccd均处于[0,1]区间。

在进行低通滤波时,只需要将遥感成像仪器的MTF、MTFoptic、MTFccd输入,便能够获得最优Butter worth滤波器,完成图像的预处理工作。

3 多帧遥感图像复原实现

3.1 遥感光学系统成像反演

遥感图像实际上是经过两次傅里叶变换后的光学影像,图像受大气湍流和成像仪器影响程度更高,而相位差异法能充分利用遥感图像的多帧通道,同时获取一对存在已知相位差的短曝光图像,联合求解波前相位分布。基于相位差异法的图像复原实质上是一种成像过程的反演描述[11],并且凭借多帧多通道避免出现单一样本反描述的病态问题[12],使复原结果噪声剔除干净且不会影响目标本身特征,增强整体信噪比。

根据相位差异法的反演特性,本文对遥感成像进行系统性分析,成像流程如图1所示。

图1 多帧遥感成像流程

根据图1能够看到成像中有2个通道即焦面和离焦面,根据实际需要还可以增添通道,光波拼接分束器同时在2台CCD相机上成像,需要一对CCD处于离焦面和焦面位置进行短曝光连续采集[13],得到目标瞬时波前的相位数据。

3.2 相位差异法代价函数

经Butter worth低通滤波器处理后,可以令式(1)内Ni(x,y)处于均值为0的状态,这时Gi(x,y)可视作是服从均值为I(x,y)·Hi(x,y)的高斯变量,将高斯概率分布σ2[14]带入到式(1)中,可转换表示为

P[Gi(x,y);I(x,y),Hi(x,y)]

(5)

再使用最大似然估计进行对应变换,并省略常数项,将式(5)改写为

L[Gi(x,y);I(x,y),Hi(x,y)]

=|Gi(x,y)-I(x,y)·Hi(x,y)|2

(6)

凭借帕斯瓦尔定理进行傅里叶变换,得出

L[I(x,y),Hi(x,y)]=

|P(fx,fy)-Q(fx,fy)·OTF(fx,fy)|2

(7)

式中,P、Q表示多通道频域中的图像、输入的光场分布,f表示离焦,传递函数OTF属于点扩散的傅里叶变换表达函数。

(8)

式中,j表示光瞳处畸变波前的相位系数,F表示傅里叶变换,l表示图1中已知离焦距离,φl表示离焦相位,θ表示成像系统的光学畸变相位。使用极坐标下的泽尼克对φl进行多项式表示

φl=αt(2ζ2-1)

(9)

式中,αt表示离焦项的泽尼克系数,t表示总帧数,ζ表示多项式所处范围极径。设光学成像的光瞳孔的直径为D,λ表示光瞳范围,αt的表达式为

(10)

综合上述公式能够推导出,多帧遥感图像泽尼克系数和光场最大似然函数表示为

L[αt(x,y),αt]=

|P(fx,fy)-Q(fx,fy)·OTF(fx,fy)|2

+|Pl(fx,fy)-Q(fx,fy)·OTFl(fx,fy)|2

(11)

式中,P(fx,fy)与Pl(fx,fy)、OTF(fx,fy)与OTFl(fx,fy)分别表示焦面和离焦面的光学传递函数、光场分布。输入光场的分布维度Q(fx,fy)跨度越大,求解最大似然函数的难度越高,因此,将式(11)转换为

(12)

式中,*表示复共轭操作。再求解仅关于αt的最大似然解值:

“slight”意指“to treat sb.rudely,without respect;or as of unimportant”，译成“侮慢，轻视；冷落”。作为全书的中心人物，伊丽莎白虽然比不上姐姐吉英漂亮，但她资质聪明，思想活泼，开朗幽默，即使舞会上男宾少，也不至于受到舞伴们的侮慢轻视，此处译成“冷眼看待[4]”是不合适的，“are slighted”取其第二条释义，译为“受到别人冷落”更为恰当。

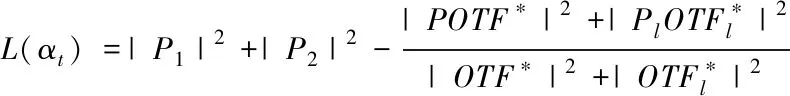
(13)

3.3 正则化约束

为此将最大似然估计转换为最小二乘问题(CLS),进行约束

(14)

(15)

(16)

式中,C2表示先验信息的约束条件,通过实际遥感图像和理想图像间的差值求出。联立式(14)-(16)得出统一的无约束表达式为:

(17)

将正则化因子代入式(12)、(13)进行正则化约束:

(18)

(19)

根据约束处理后复原目标函数和差异法代价函数,得出似然函数的最小可行解,即可恢复遥感降质图像分辨率,展现更多有效特征。

4 实验分析

本文通过评价复原后遥感图像质量,来判断所提复原方法的优劣,这对于后续的深入研究有指导性的作用。

4.1 实验数据集与评价指标

实验所用遥感图像来自UCMerced LandUse数据集,图像尺寸为256×256,空间分辨率为0.3m。本文在开源遥感图像数据集中随机挑选2组图像,第一组遥感目标为城市建筑,第二组为城市边缘乡村道路。实验分为定性和定量两部分,定性实质上就是以人眼对复原结果进行主观评价;定量则是使用能够描述图像特征的参数和物理量,来对比复原前后的图像质量变化。

4.2 复原后图像定性评价

原始降质图像和复原后图像如图2、3所示。

图2 城市多帧遥感图像复原效果

图3 乡村多帧遥感图像复原效果

通过对比能够看出,复原后图像的目标边缘更加清晰,且包含的细节丰富,不同个体的特征突出,能够很容易分清建筑物的边缘轮廓和道路走向。这主要是因为本文方法采用相位差异法修正遥感图像的波前畸变,并通过正则化约束目标函数和代价函数,避免图像陷入病态化问题中,以此提升了图像复原质量。

4.3 复原后图像定性评价

定性评价虽然是可靠的,但是所得出的评价结果并不稳定,不同观察者或处于不同观察环境所得出的定性评价都会产生细微差别。为此,进一步使用定量评价方法分析图像复原效果。

1)灰度平均梯度(GMG),表示对目标图像水平长度U和垂直长度V上的邻域像素灰度作差,通过计算平方和再求得均方根值。表达式为

(20)

式中,g(x,y)表示像素灰度。

2)拉普拉斯梯度模(LS),表示选定一个像素,划分邻域3*3范围,使用Laplacian算子进行微分计算,获得目标像素的8个邻域微分,再求和获得。表达式为

(21)

3)Fisher信息量(FI),描述遥感图像灰度概率的梯度平方和,表达式为

(22)

式中,k表示迭代次数,B(ik)用于描述图像内灰度值是ik像素出现的概率值,可表示为

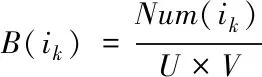
(23)

式中,Num(ik)表示整幅图像内ik出现的像素数量。

由于遥感图像内包含细节信息量多,所以图像任意像素与邻近像素的灰度值差异大,或不同灰度的像素值出现概率波动越剧烈,都表示图像清晰度高及图像复原质量好,可得出若LS、FI、GMG值越大,就能够证明复原后图像相比初始图像质量高,噪声少。表1为复原图像的定量评价结果。

表1 复原前后定量评价

通过表1中的复原前后LS、FI、GMG值对比能够看出,复原后的指标都有所提升,且第一组的复原指标值最大,这是因为第一组主要为城市建筑和街道,包含的细节信息比第二组农田山林要更多。深入分析本文方法复原效果较好的原因在于,相位差异法能够在遥感成像中独立使用,既不受限于遥感仪器分辨率、零部件等硬件条件,也不约束自然环境,具有较好的适应性,能够修正大气湍流和光学系统的双重误差,因此,有效提升了图像复原效果。

5 结论

本文提出了基于相位差异法的多帧遥感图像复原方法,不仅弥补了部分画质低问题,还有效剔除了图像内高频位置的随机干扰,增强了目标特征。实验从定性和定量两个角度出发,证明所提方法不仅主观评价质量高且客观图像像素灰度特征、清晰度都有大幅度提高。该方法可以复原遥感降质图像,提高图像分辨率,增强细节特征边缘强度,丰富画面内容,为用户提供更多的信息量。