建筑地基深基坑开挖底面下沉监测模型仿真

余晓雅,张海清

(河北大学建筑工程学院,河北 保定 071002)

1 引言

建筑施工过程中,地基深基坑的开挖势必引起地基内应力场变化,土体和周边建筑物产生形变,影响工程质量[1,2],严重则会产生楼体坍塌事故,带来重大经济损失,威胁人民群众生命安全。所以对基坑开挖底面下沉风险监测是十分必要的,这也是当前建筑领域研究的核心问题[3]。

针对建筑深基坑的风险监测问题,现阶段学者们给出了如下典型处理方案:李宏钊等人[4]提出一种基于空间遥地耦合探测技术的建筑地基监测方法。使用遥感信息探测得到建筑参数,融合遥感探测、工程分析参数与建筑空间测算,构成用来计算地基形变的探测技术。王晓磊等人[5]提出基于GA-BP神经网络的地基纠偏沉降预测方法。在遗传算法-反向传播(Genetic Algorithm-Back Propagation,GA-BP)神经网络基础上,将掏土量和掏土方位拟作控制参数,分析建筑底板沉降情况,完成地基纠偏过程评估。但以上两种方法计算复杂度高,且输出风险监测结果时间较长。

由此,提出一种基于改进极限学习机的基坑底面下沉风险监测方法。剖析现阶段基坑底面下沉真实状况,从不同层面划分基坑底面下沉风险评估指标,利用改进极限学习机方法实现基坑底面下沉风险监测,在实验中进一步验证了所提方法有效性,能为高效率建筑施工发挥重要作用。

2 基坑开挖底面下沉模态

为进一步明确基坑开挖底面下沉情况,分析基坑开挖地面形变过程。在形变特点剖析中,地基会受到静水压力的作用,且不考虑重度梯度影响[6]。融合构件滞回特点,利用松弛参数分析底面应力与屈服响应。使用最大累计下沉控制策略研究建筑地基深基坑开挖下沉模式与形态。

设定深基坑开挖的单元应力矢量是a,应变矢量是β,基坑底面中产生网状缝隙的解析式为

(1)

其中,am、βm依次表示总测量点的缝隙开展度与钢筋屈服,i表示其中任意测量点。

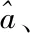
(2)

其中,

(3)

(4)

式中,bmn表示弹性因子,C表示压力数据弹性模量,Gi为第i组形变方位节点的板角约束力,Ei为基坑底面竖向挠度。

按照以上内容,即可实现建筑地基深基坑开挖底面形变参数模拟,得到现阶段基坑底面下沉的真实情况,为后续下沉风险监测提供理论支持。

3 风险评估体系构建

基坑开挖底面下沉存在很多风险元素,如果不精准辨别隐含风险源,会延误建筑施工进度[9]。建筑地基基坑开挖时,具备如下风险元素:

1)自然状态:地质、水文、气候等;

2)所处环境:周边建筑物、地下管线(涵盖管道埋深、材质、竣工时间)、周边道路状况等;

3)结构特点:基坑开挖深度、宽度、基坑围护结构等;

4)施工元素:排水措施、场地布置、施工模式、机械选择、工程顺序等。

建筑深基坑施工是一项内容丰富、颇具风险的工程,尤其是在雨季,由于地质条件、地下水状况、天气变化、施工次序及周边环境,极大影响了深基坑施工进度[10]。在此基础上,采用层次分析法来评价基坑工程底面下沉危险性。层次分析法将定性与定量相结合,将一个复杂的系统划分为多个子系统[11],构成了一个有序、多层的层级结构。基坑底面下沉风险评价包括目标层、准则层与指标层,将其表示成图1。

图1 基坑底面下沉风险评估体系示意图

4 风险监测方法

根据基坑地面下沉风险评估体系,利用改进极限学习机监测基坑地面下沉风险。为有效提升基坑底面下沉风险监测精度与速率,提出一种基于改进极限学习机的基坑底面下沉风险监测方法。极限学习机网络训练模型使用复杂度最小的单隐层架构[12],如果输入层、隐含层、输出层的节点依次是c、H、1,那么将极限学习机的网络架构表示成图2。

图2 极限学习机网络架构

针对固定数据集K={(x1,y1),L,(x1,y1)},将极限学习机数据训练模型描述成

(5)

其中,αi、oi依次表示输出层神经元、输入层神经元和第i个隐含层节点的连接权重,pi是第i个隐含层节点的偏置,xi为训练数量,l(x)表示隐含层输出矩阵。

训练开始前,预先选择原始输入权重oi与偏置pi。同时在训练中oi的值固定不变[13],输出权重αi可利用式(6)获取

(6)

其中,yi代表第i个隐含层节点总数。

极限学习机方法将训练偏差最低作为输出结果的衡量准则,导致在训练时极易产生过拟合现象[14],减少了基坑底面下沉风险检测结果的准确性。面向此类问题,设计一种融合经验风险最小与结构风险最小的改进极限学习机方法。把式(6)的方程变换为

(7)

在式(7)内引入拉格朗日算子,得到

(8)

其中,φi代表拉格朗日算子。

利用最优化定理,设置Q对α、φi的偏导均为0,即可获得以下线性方程

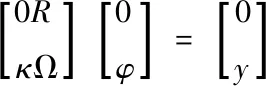
(9)

其中,R表示偏导因子,κ为非零常数,Ω代表方阵。将方阵内的元素值记作

Ωij=[(o1,p1,xi)·(o1,p1,xj)]

(10)

在式(8)、(9)中可知,在建模改进极限学习机法时无需计算隐含层偏置pi,增强训练计算效率,并全方面考虑了经验风险与结构风险两种要素,在一定程度上减少过拟合现象。

建筑地基深基坑开挖底面下沉风险监测的具体步骤如下:

步骤1,归一化处理。训练数据前,要对数据预处理。归一化条件属性是训练样本的输入数据,决策属性是输出数据,使用离散化处理全部数据属性,得到基坑开挖底面下沉数据的决策表。将r类样本的能量均值描述成

(11)

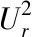
归一化处理的本质就是把数据依照比例投射至某个区间,通常使用极值法完成归一化过程,这里将其定义为

(12)

其中,xmin为数据序列内的最小值,xmax为数据序列内的最大值。

步骤2,计算延迟步数。为明确最优的网络输入架构,要获得其具体的延迟步数[15]。针对时间序列z而言,推算其延迟步数的自相关指数u(q)即可得到延迟步数的值,将其运算过程表述成

(13)

若自相关指数u(q)符合式(14)的约束条件,那么该时间序列延迟步数的相关性较为明显,反之相关性较差。

(14)

其中,M代表训练迭代次数,u是延迟步数平均值。

步骤3,确立风险监测临界值。建筑基坑下沉值d≤10mm,证明其处于低风险,10≤d≤30mm表明处于中风险,30≤d≤50mm证明处于高风险。

步骤3,构建训练模型。确立了延迟步数后,就能获得各层网络结构节点数量并创建基坑底面下沉风险监测训练模型,记作

(15)

5 实验分析

为证明研究方法的应用可行性,设计对比实验分析不同方法的性能差异,将文献[4]提出的基于空间遥地耦合探测技术的建筑地基监测方法(遥地耦合探测方法)和文献[5]提出的基于GA-BP神经网络的地基沉降预测方法(GA-BP神经网络方法)作为对照组,实验平台为MATLAB 7.0,实验地点为某市正在施工的建筑,在该软件平台上构建建筑地基模型,如图3所示。

图3 实验建筑深地基模型

该建筑围护结构使用900m厚地下连续墙,主体架构基坑开挖深度是16～19m,设定该基坑包含1道砼支撑与6道钢支撑。建筑周边具备较多建筑物,其中距离最近的是1栋6层砖混架构民房,距离基坑只有5m左右。待施工建筑使用条形基础,基础埋深约为2.5m,条形基础下方是15m深度的深层搅拌桩地基加固,加固体和基坑之间的距离为0.8～4.5m。将实验划分为三个阶段,分别为降水阶段、注浆阶段和开挖失水阶段,监测日期为2021年8月5日～10月15日,挑选较有代表性下沉数据的日期为分析目标,对比真实基坑底面沉降值与三种方法下得到的沉降值,实验结果如图4～6所示。

图4 降水阶段地基下沉累计变化值

图5 注浆阶段地基下沉累计变化值

根据图4～图6所得数据可知,降水阶段得到的最高下沉值为-8mm,注浆阶段在地表有部分隆起,最高隆起约为6mm,降水仅能把水位下降到岩土分界面,深基坑开挖失水期部分裂隙有水溢出,又一次引发基坑底面下沉,得到最终的基坑开挖下沉真实值为-15.5mm,所提方法下沉值为-16mm,遥地耦合探测方法、GA-BP神经网络方法得到的下沉值依次为-20mm和-18mm。可以看到,当前基坑底面下沉处于中等风险,应采取对应措施避免底面下沉情况继续恶化,这也与实际施工情况基本相符。

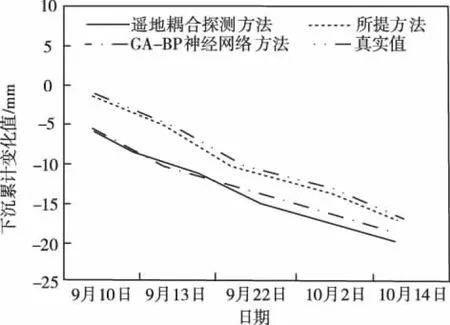
图6 开挖失水阶段地基下沉累计变化值

为证明所提方法可靠性,使用三种方法评估建筑地基深基坑开挖底面下沉中存在的风险,比较不同方法的误判率,实验结果如图7所示。

图7 三种方法基坑底面下沉风险监测误判率对比

根据图7实验结果可知,所提方法在下沉风险评估方面具备较低误判率,四种风险元素的误判率均保持在5%以下,遥地耦合探测方法、GA-BP神经网络方法的风险监测误判率分别处在10%、7.5%左右。这是因为所提方法风险评估前首先采取分析基坑形变特点,得到较为真实的计算数据,大大提升了后续下沉风险监测的准确性。

设定基坑底面下沉风险监测实验的迭代次数为800次,以耗时指标为测试指标,对比三种方法在风险监测时效性方面的优劣,结果如图8所示。

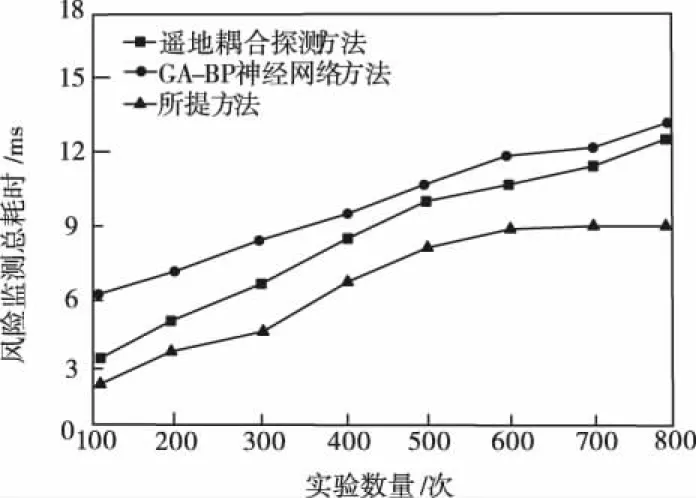
图8 三种方法时对比

从图8可知,伴随实验数量的增多,三种方法的监测总耗时呈上升趋势,但所提方法耗时增长速率较为缓慢,且在第600次实验后基本保持在8ms～9ms,说明该方法具备更强的适用性。

6 结论

建筑地基深基坑底面下沉风险监测受到较多因素影响,属于一种复杂不确定性问题,为更好地分析底面下沉风险情况,提出基于改进极限学习机的基坑底面下沉风险监测方法。推算基坑底面网状缝隙,分析载荷-平面移动分布弹性模量与裂缝开展度、钢筋屈服间的内在关联,获得底面下沉实时状态,创建基坑底面下沉风险评估体系,在极限学习机方法中代入经验风险最小与结构风险最小条件,获得高精度基坑下沉风险监测输出结果。所提方法计算简便、实用性强,可为建筑工程施工风险评估提供新的计算思路。