基于遗忘PI自适应滤波在车载导航中的应用
2023-07-03郭秀灵孙立功
郭秀灵,孙立功
(河南科技大学电气工程学院,河南 洛阳 471023)
1 引言
随着导航技术的不断发展,车辆导航定位技术受到越来越多学者的关注。由于高精度的惯导产品价格高,难以大量应用于民用车辆,因此,该领域的学者们也在不影响导航精度的情况下,通过提出新的导航算法来减少车载导航的成本,为民用车辆使用惯导设备创造了条件[1]。常规的卡尔曼滤波算法应用于导航系统时,需要精确的数学模型以及确切的系统噪声和量测噪声,但在实际的应用中,量测噪声和系统噪声准确的特征值很难获得[2]。针对上述问题,可采用自适应的卡尔曼滤波算法(Adaptive Kalman Filter, AKF)的非线性滤波来进行估计出定位信息[3]。
自适应卡尔曼滤波算法通过用测量数据来实现滤波推算,同时,判断系统的动态是否发生变化。若动态发生变化将其看成随机干扰归算到模型及噪声中去,对模型参数和噪声进行估计和及时修正来适应系统动态的变化。自适应卡尔曼滤波方法有多种,包括Sage-Husa自适应滤波、自适应扩展卡尔曼滤波算法、渐消因子滤波[4-6]。其中Sage-Husa自适应滤波运用自适应噪声协方差矩阵可以修正一定的噪声统计特性,但对于较高阶次的系统时滤波输出的结果易发散;自适应扩展卡尔曼滤波算法通过对新息协方差的测量与计算,对卡尔曼滤波器的增益矩阵进行自适应修正,但运算过程中存在计算量大的问题,解算结果出现发散的情况;而渐消因子滤波能在一定程度上修正模型误差引起的系统噪声。
针对上述问题,本文提出了一种基于遗忘因子PI自适应滤波算法在车载导航中的应用。该算法将PI控制器与卡尔曼滤波器结合,可实现对观测噪声协方差矩阵进行在线修正,来提高导航的精度。自适应卡尔曼滤波是通过新息序列的协方差估计值和理论值构造函数来选取遗忘因子,以此来限制卡尔曼滤波器的记忆长度,调整新息的权重,充分利用现时的观测数据,随着时间的推进,滤波器逐渐消除建模不准确或量测噪声的多变的影响,达到滤波抑制滤波发散的目的[7-9]。
2 常规自适应滤波模型建立
自适应卡尔曼滤波能对观测噪声协方差矩阵进行实时估计并修正,从而抑制发散,实现快速收敛,并减小误差。自适应滤波在进行状态估计时,同时通过量测输出在线实时地估计系统的噪声参数,但是对于车载导航系统来说,由于加速度计易受振动以及运动加速度干扰,观测噪声协方差矩阵是时变的,实现所有的噪声参数进行估计是不可能的,因此,假设量测噪声方差阵未知的。
2.1 常规自适应系统模型
导航系统随机系统状态空间模型,如下
Xk=Φk/k-1Xk-1+Γk/k-1Wk-1
Zk=HkXk+Vk
(1)
其中Xk是n×1维的状态向量,Zk是m×1维的量测向量;Φk/k-1,Γk/k-1,Hk是已知的系统结构参数,分别称为n×n维的状态一步转移矩阵、n×l维的系统噪声分配矩阵、m×n维的量测矩阵,Wk-1是l×1维的系统噪声向量,Vk是m×1维的量测噪声向量,两者都是零均值的高斯白噪声向量序列,服从正态分布,且它们之间互不相关,即满足

(2)

2.2 量测噪声方差阵的求解
在自适应滤波算法中,量测噪声方差阵Rk是未知的。下面关于Rk的自适应估计的方法计算[10-14]。
由自适应卡尔曼滤波状态估计计算方程得,k时刻的实测滤波残差即新息为
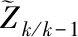

(3)
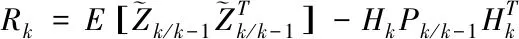
(4)


(5)
2.3 常规自适应的卡尔曼滤波的计算步骤
由上述分析,可得自适应的卡尔曼滤波的公式如下

(6)
3 PI自适应卡尔曼滤波算法
该算法对观测噪声协方差矩阵进行调整,通过残差方差的实际值和理论值的误差值,利用PI调节器来进行实时调节和控制。PI自适应卡尔曼滤波算法,通过修改滤波算法公式实现,将时变观测噪声协方差矩阵rk来代替Rk[15]。
定义残差方差的理论值为

(7)
定义残差方差的实际值为
Ck=(Zk-Hkk/k-1)
(8)
残差方差理论值与实际值之间的差值可以用两个矩阵的迹之差来表示,即
Ek=trace(Dk)-trace(Ck)
(9)
自适应卡尔曼滤波算法的关键在于求解调整系数αk。残差方差的理论值Dk是随观测噪声协方差矩阵Rk逐渐递增的,因此,通过调节Rk来改变残差方差的理论值,使Ek的值在0附近。
在实际应用中,通过引入PI控制器来更好地控制Ek的值。控制器的调整系数αk的求解公式如下

(10)
式(10)中,Kp为比例系数,可快速消除误差,Ki为积分系数,可用于消除静态误差。该PI控制算法,为防止积分饱和,可通过引入积分分离来实现。积分开关系数β的设置如下

(11)
式(11)中,ε为开关阈值,可根据实际情况选定。当残差方差误差Ek大于阈值时,不使用积分环节,防止饱和;反之,积分环节介入,来消除余差。
自适应卡尔曼滤波增益计算公式如下

(12)
其中,rk=(1+αk)rk-1为第k次迭代时观测噪声协方差矩阵的估计值,αk为观测噪声协方差矩阵的调整系数。由此,可得PI自适应的卡尔曼滤波的公式如下

(13)
4 遗忘因子的选取
为减轻滤波过渡收敛的情况,使得状态估计能较好地适应新的量测值变化,引入了遗忘滤波的算法,在滤波过程中修改系统噪声Qk和量测噪声Rk的权重,来逐渐减小历史信息的权重,提高了新信息的权重,达到减小滤波器惯性的目的。遗忘滤波在自适应系统建模的情况下能进一步改善了滤波精度[6-8,12]。
该系统的状态空间模型如式(1)所示。对于一个有限时间序列N,噪声的方差阵变为
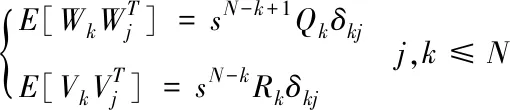
(14)
通过整理可得,带由遗忘因子的自适应卡尔曼滤波的公式如下

(15)
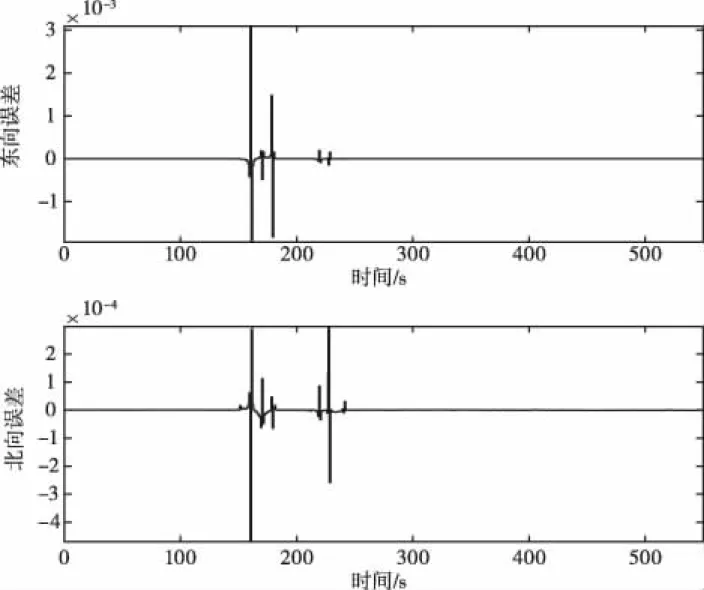
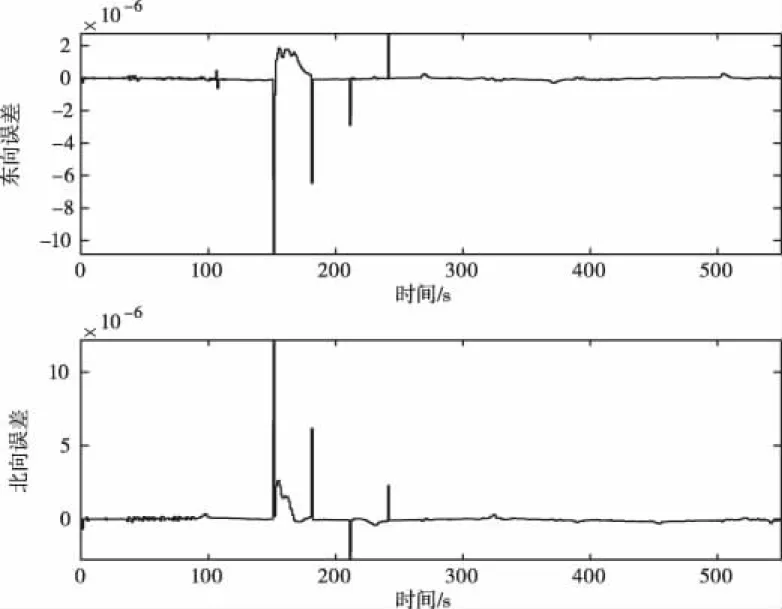
式(15)中,s为遗忘因子,取值范围为0 由上述可知,本文采用自适应遗忘滤波方法,随着滤波的进行,利用遗忘因子给旧的历史数据越小的加权系数,降低旧数据在滤波中的作用,增大新数据的加权系数,以抑制滤波发散,提高新数据的利用率,从而来改善滤波器的动态性能。 为验证具有遗忘PI自适应卡尔曼滤波算法的有效性和精确性,通过500秒左右的跑车实验来进行收集数据。通过加载该数据并通过matlab进行验算,分别用常规的自适应滤波算法、PI自适应卡尔曼滤波算法、遗忘PI自适应滤波算法来进行解算,得到的行车轨迹与实际的行车轨迹(GPS高斯—克吕格投影)对比,如图1、2、3所示。 图1 常规的自适应滤波算法解算轨迹 从图1中,可以看出常规的自适应滤波算法,在解算的过程中,受到环境的影响和其它因素的干扰的,解算出的轨迹与实际的轨迹进行对比,部分误差较大。为改善上述轨迹发生的误差波动,通过采用PI自适应滤波算法来实现,结果有较好的修正,如图2所示,但解算出的轨迹与实际轨迹相比还有误差,如果继续用这些波动作为白噪声,还会引起大的误差。因此,PI自适应滤波算法通过加入遗忘因子来加权系数,抑制滤波的发散,从而有效克服波动,该算法解算出的轨迹如图3所示,可以看出解算出的轨迹与实际轨迹相比,误差极其小。 图2 PI自适应卡尔曼滤波算法解算轨迹 图3 遗忘PI自适应卡尔曼滤波算法解算轨迹 如图4~6分别为常规自适应滤波算法、PI自适应卡尔曼滤波算法、遗忘PI自适应滤波算法在东向、北向上解算出的位置误差图。从上面的误差图及轨迹图可以看出,行车150~250秒时间,位置误差波动较剧烈。通过常规自适应滤波算法解算时,位置误差波动较为频繁而且幅值较大。PI自适应滤波算法解算时,波动没有减少,但误差的幅值减小了。而遗忘PI自适应滤波算法,波动减少了,同时误差幅值也减小了。由此可得,具有遗忘因子PI自适应滤波算法自适应卡尔曼滤波算法的解算精度最高,其次是自适应卡尔曼滤波算法,最后是常规自适应滤波算法。在实际应用中,随机动态系统的结构参数和噪声统计特性参数的获取都会或多或少存在一些误差,致使卡尔曼滤波的精度降低,严重时还很可能会引起滤波发散,而自适应滤波算法能改善部分参数的影响,但是自适应滤波并不是万能的,在滤波计算回路不再是简单线性的,是一个较复杂的非线性系统,实现起来较复杂,而遗忘PI自适应滤波算法是在自适应滤波算法的基础上,通过PI控制实现在线修正,通过引入遗忘因子减轻过渡收敛症状,同时也减小历史信息的权重,相对而言提高了新信息的权重,从而减少旧量测数据的影响,对噪声矩阵的调整更加连续,因此该算法滤波效果相对稳定。 图4 常规自适应滤波解算位置误差 图5 PI自适应滤波解算位置误差 图6 遗忘PI自适应滤波解算位置误差 本文在自适应卡尔尔曼滤波的基础上提出了一种基于具有遗忘PI自适应的卡尔曼滤波算法。通过对量测噪声协方差矩阵进行遗忘因子实时估计以及通过PI控制的在线调整,保证了该算法的精度,增强了其在工程上的应用价值。实验结果表明,改进后的算法能有效的抑制滤波发散,比常规的自适应滤波的效果更好,导航的精度有极大提高,同时系统的稳定性也有所提高。车载试验的结果也验证了该算法的正确性以及实用性,这也为车载导航的进一步提高导航精度的研究提供有利的保证。5 试验结果与分析




6 结论
