自适应RBF神经网络在燃气流量调节中的应用
2023-07-03齐胜举薛海峰魏岩淞
齐胜举,陈 雄,薛海峰,魏岩淞
(南京理工大学机械工程学院,江苏 南京 210094)
1 引言
固体火箭冲压发动机(以下简称固冲发动机)是一种吸气式固体火箭发动机,是一种新型动力装置[1,2],结合了冲压技术和固体火箭技术,携带贫氧推进剂,利用空气中的氧作为推进剂燃烧过程的氧化剂,具有比冲大、可靠性高等优点[3]。
固冲发动机工作过程中,空燃比是衡量其工作性能的一项重要的指标。进入补燃室中的空气流量会受到飞行高度、攻角以及飞行速度等因素影响。燃气流量调节技术的应用,不仅大大能够防止发动机因补燃室中进气量过大或过小造成不良影响[4,5],同时能够能够实现推力可控可调,对提升武器系统的可靠性、机动性和精确打击能力都有着重大的意义,因此燃气流量可调固冲发动机一直是现在研究的热点问题[6-9]。
在众多燃气流量调节的方案中,变喉面式燃气流量调节方法具有可控性强、抗干扰能力强、控制精度高等众多优点,国内外诸多科研人员对其进行了很多研究[10-12]。欧洲对于改技术的研究较为先进,其装备部队的“流星”超视距空空导弹的燃气流量调节比最大可达达到了12:1[13-17];俄罗斯的R-77M导弹的固冲发动机采用针阀方案,使得燃气流量调节比可达9:1[18];我国哈尔滨工业大学的鲍文、牛文玉等人对燃气发生器的动态特性进行研究,发现燃气流量调节系统的非线性和变参性的特点对系统有较大影响[19-22];刘源翔、周景亮等人均利用了自抗扰控制算法,对燃气流量调节系统进行研究,大大提高了系统的控制精度,并使系统具有了一定的抗扰能力[23,24];周俊、余业辉利用神经网络智能算法结合PID,改善了PID算法对非线性系统控制的适应性[25,26]。
以上算法均使用了小扰动线性化模型对系统特性进行分析,并依据线性化模型进行算法设计,这使得算法能够在某压强处有良好的控制精度,但并为做全局状态下扩展,很可能出现较大的控制误差。另外从以上控制算法的仿真结果看这些算法的使用均能够使燃气发生器内部的压强达到一定的控制精度,但同时能够明显发现无论是自抗扰还是神经网络算法,系统的稳定时间均有明显的增加,这直接影响了长时间工作时固冲发动机的性能。所以针对以上两点不足,本文采用了反馈线性化的线性化方法,对模型进行了全局线性化;另外通过对燃气流量调节系统的分析可知,燃气发生器自由容积的变化影响了控制算法的稳定时间,而且由于自由容积无法直接测量,所以在实际控制系统中无法通过直接反馈的方式进行补偿,因此本文应用了一个非线性滑模观测器对此参量进行实时观测,并补偿到控制量中,从而抑制其对控制精度的影响;另外,在控制算法中结合了滑模算法,使整个系统具有一定的鲁棒性,降低了数学模型误差和参数误差对实际系统中控制效果的影响。
2 燃气流量控制原理以及系统模型
2.1 燃气流量控制原理
本文的研究对象采用的是壅塞式燃气流量调节方式,即燃气发生器喉部始终处于壅塞状态,通过改变喉部面积,能够改变器内部压强,进而改变燃气的质量流率。由于燃气的质量流率无法直接测量,所以选择燃气发生器内部压强作为控制系统的被控量。燃气流量调节控制原理如图1,图中Pd为目标参考信号,Pg为燃气发生器内部压强,Ps为压力传感器所测得的系统压强。燃气发生器工作时,通过压力传感器实时测量Pg,并将其反馈至控制器,控制器根据Pd和Ps通过合适的算法产生控制信号u,执行机构根据控制信号作动,改变燃气发生器的有效喉部面积,使得Pg能够快速、准确的跟踪Pd。

图1 燃气流量调节系统控制流程
2.2 系统数学模型及分析
由于燃气发生器喉部一直处于壅塞状态,所以燃气发生器被可以看作一个小型的固体火箭发动机。为了方便对燃气发生器展开数学模型分析对燃气发生器模型做出如下假设:
1)假设推进剂在燃气发生器内完全燃烧,并且燃烧过程中燃烧温度和特征速度均不变;
2)假设燃烧产生的气体为组分不变的理想气体;
3)假设药柱燃面大小不变,并且燃速处处相等,而且满足指数燃速定律;
4)假设燃气发生器内各处的压强完全一致,只是与时间相关的平均压强。
根据以上假设,结合质量守恒定律,计算燃气发生器内部的压强满足如下方程
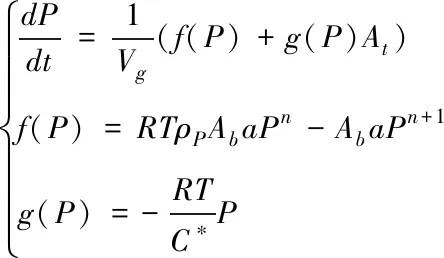
(1)
式中Vg为燃气发生器自由容积,随着推进剂燃烧逐渐变大的有界参量;Ab为推进剂燃烧面积;a和n分别为推进剂的燃速系数和燃速压强指数;P为燃气发生器内部压强;ρp为推进剂密度;C*为推进剂特征速度;At为燃气发生器喉部面积,并且Atmin≤At≤Atmax。
任意取一个平衡点(P0,At0),在此平衡点处将(1)式进行一阶泰勒展开。令ΔP=P-P0,ΔAt=At-At0,计算得在此平衡点处的小扰动线性化模型如下

(2)
对(2)式进行Laplace变换,得到在此平衡点处得燃气流量系统的传递方程如下:
(3)
由于平衡点选择具有任意性,并且推进剂得燃速压强指数n小于1,所以根据燃气发生器的传递函数模型可知,燃气流量调节系统的极点始终位于复平面左侧。因此燃气流量调节系统是一个输入有界,并且具有全局一致稳定性的非线性系统。进一步分析可知,此系统的稳定时间和燃气发生器工作状态有关,具体表现为燃气发生器内压强越小、自由容积越大,系统稳定时间越长。所以固冲发动机在不同的工作状态会导致被控系统表现不同的特性,即此系统存在变参性的特点,而参数的变化主要影响系统的响应速度,并不会对系统的稳定性造成影响。
固冲发动机只有在超音速的条件才能正常工作,所以控制系统的主要设计目的为:设计一种控制算法,使系统输入u∈[Atmin,Atmax],同时保证燃气发生器压强能够快速响应,并有效的跟踪目标参考压强。
3 自适应RBF神经网络控制器设计
由式(1)的燃气发生器数学模型可知,该控制系统具有强非线性、强时变性的特点。而小扰动线性化方法只能够保证在所选取的平衡点附近对原系统的近似精度,无法满足在固冲发动机工作全域内对原系统的近似。而PID控制算法虽然具有很强的鲁棒性,但其控制参数必须相对于某一特定参数进行整定,并且参数的整定需要大量的经验,所以整定后的参数只能保证对于某一特定的工况控制效果。所以对于燃气流量调节系统来说,无法保证在其工作范围的全域内对压强的精确控制。
因此本文针对此模型设计了一个基于自适应RBF神经网络的变结构控制器。由于系统的非线性主要来自于模型中的f(P)部分,而g(P)部分的相关参数由推进剂厂商根据实验结果给出,具有一定的精度,所以本文利用RBF神经网络对任意函数的逼近能力,只对系统非线性部分f(P)进行辨识[27-29],并采用反馈线性化方法对系统进行补偿,抑制非线性部分对被控系统的影响[30,31];另外结合自适应算法和变结构控制使模型能够在具有良好得跟踪效果的同时,具有一定的抗扰动能力。
3.1 理想控制律设计
为了实现燃气发生器压强的精确控制,定义系统的跟踪误差
e=P-Pd
(4)
考虑有界扰动Δ,对被控系统得数学模型进一步整理为:

(5)
对(5)式分析可知燃气发生器是一个相对阶P=1的一阶非线性系统,并且满足可反馈线性化的标准形式。基于(5)式,设计控制器理想控制律如下:

(6)
3.2 RBF神经网络原理
RBF神经网络理论上能在一个紧凑集和任意精度下,对任意函数都具有很强逼近能力。相较于多层前馈网络,RBF神经网络结构简单,避免了不必要的和冗长的计算。一个RBF神经网络由输入层、隐含层和输出层组成,其原理结构如图2所示。

图2 RBF神经网络原理图
输入层为输入神经网络的状态参量,由系统和研究人员决定,合适得输入状态对神经网络得逼近精度和调整难度有直接影响。

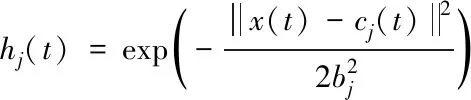
(7)
参数cj和bj的选取对神经网络能否进行有效映射有着直接的影响。在网络的设计中,要注意根据输入变量的映射范围对其进行初步设计。
输出层由式(7)所示的加权和组成,ωij为各个神经元的权重,i示输出节点的个数,yj为神经网络的输出,其形式如下

(8)
通过一定的学习规则,不断调节cj,bj,ωij能够实现神经网络对任意函数的映射。
3.3 自适应RBF神经网络控制器设计
由于燃气发生器的数学模型不可避免存在模型误差,并且在燃气发生器工作过程中存在各种扰动因素,所以本文结合自适应算法,设计了一个自适应RBF神经网络对燃气流量调节模型中f(P)进行趋近。同时利用变结构项,减小未知扰动和神经网络逼近误差对控制效果的影响,其控制原理如图3所示。

图3 自适应RBF神经网络控制系统
通过设计适当的自适应律,利用自适应RBF神经网络设计最终的控制律如下:

(9)
3.3 系统稳定性分析
设自适应RBF神经网络趋近的最优权值为

(10)
定义模型的逼近误差为
ω=(P,Pd|W*)-f(P)
(11)
取Lyapunov方程如下

(12)

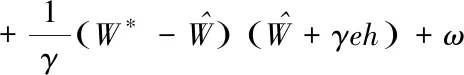
(13)
由于燃气发生器自由容积Vg恒正并且有界,另外根据RBF神经网络逼近理论,可以保证模型逼近误差ω在一定的误差范围之内,所以取适当参数K、D,就能够保证控制系统是渐近稳定的,即实现燃气发生器压强对参考信号的跟踪。同时,还能保证控制系统有良好的响应速度和抗扰动能力,满足控制系统的设计目的。
4 仿真及结果分析
为了验证本文所设计的自适应RBF神经网络控制器对燃气发生器压强的控制效果。根据图3,利用Matlab/Simulink搭建了如图4所示的燃气发生器压强闭环控制模型。通过全压强范围捏的在线控制,检验控制器在低压和高压下对燃气发生器的控制效果;选取某一特定压强,并在某时刻添加扰动信号,检验控制系统的抗扰动能力。

图4 自适应RBF神将网络控制系统
4.1 跟踪性能仿真
因为本文研究的燃气发生器具有强时变性,当燃气发生器工作时,被控对象的特性时刻发生变化,所以需要验证在较长时间下控制器的控制效果。取贫氧推进剂相关参数如表1,并输入变化范围为3MPa~9MP的参考信号,取仿真时间为30s,主要对其控制精度和响应时间进行验证。得到仿真效果如图5所示。从图中可以看出,控制系统相应很快,在0.3s内就能到达稳态,并且跟踪误差较小,稳态时得跟踪误差在1%以内,所以即使当固体火箭冲压发动机在高速运行时,也能保证良好得控制效果。
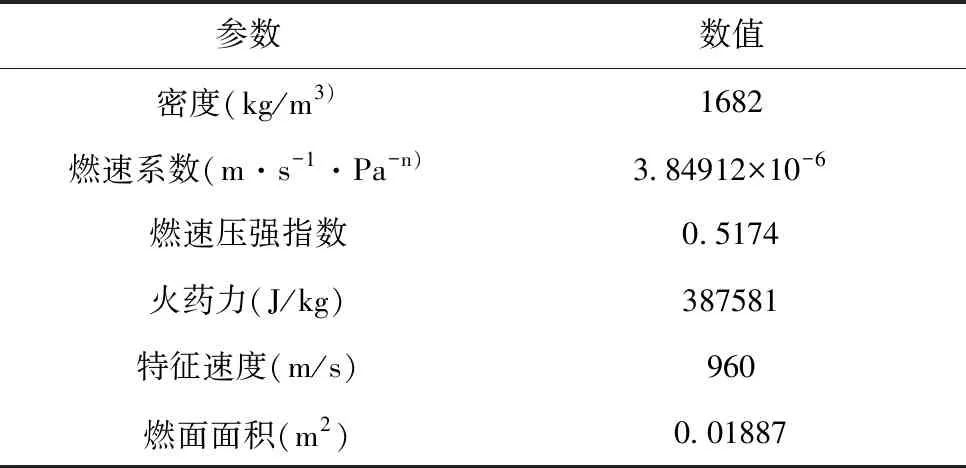
表1 某贫氧推进剂参数
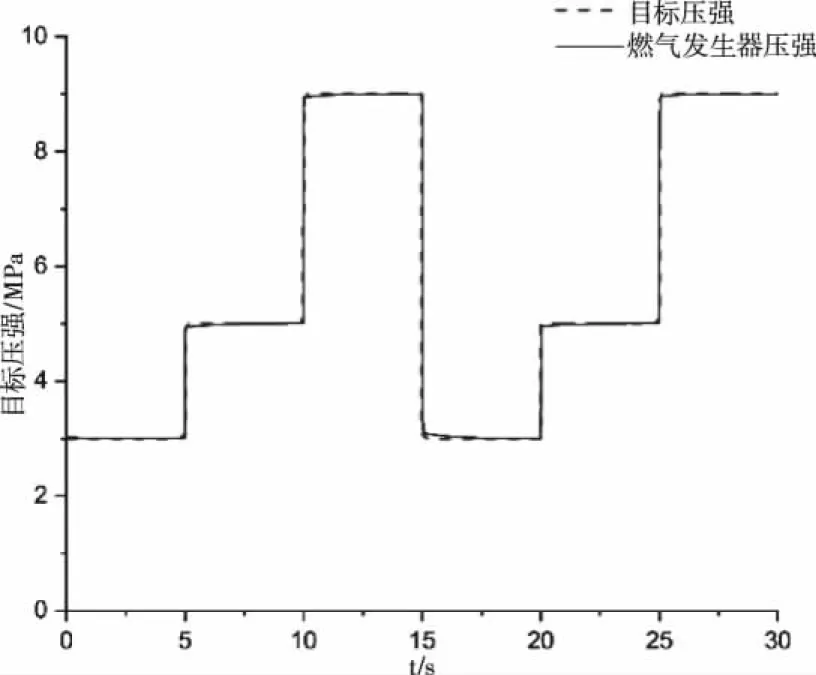
图5 自适应RB神经网络控制器控制效果图
4.2 抗扰动能力分析
取贫氧推进剂相关参数如表1,并输入变化5MPa的参考信号,在20s左右添加值为1MPa的扰动信号,得到仿真效果如图6所示。从图中可以看出,在较大的干扰情况下,燃气发生器压强依然能够快速收敛到5MPa。因此可以证明该控制器具有较强的抗干扰能力。
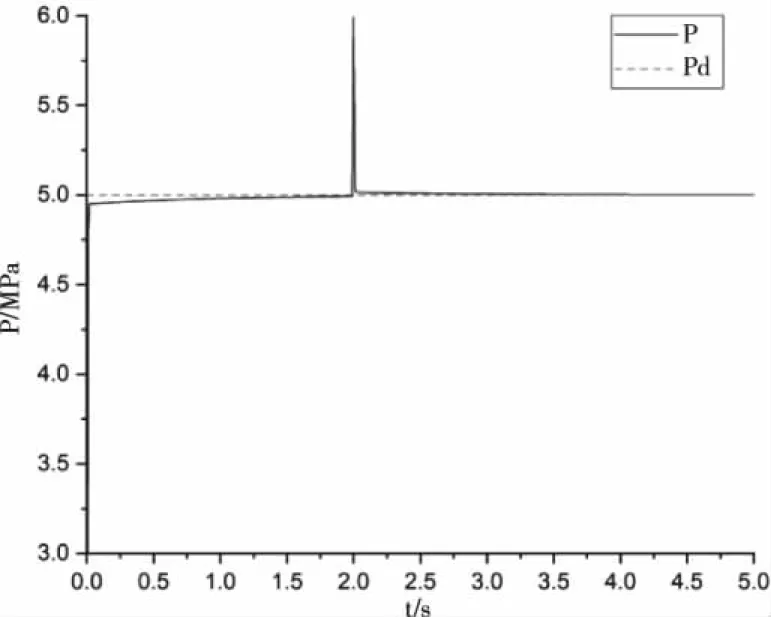
图6 系统扰动下跟踪结果
5 结论
本文通过对燃气发生器燃气流量调节系统特性及控制算法的研究,得出以下结论:
1)燃气流量调节系统是一个具有一致稳定性的、参数变化的非线性系统,系统的控制效果会受到燃气发生器的工作状态影响,具体表现为燃气发生器内部压强越高,燃气发生器内自由容积越大,系统的响应越慢。
2)针对燃气流量调节系统的特性,为了保证控制系统具有较高的控制精度、快速的响应时间和良好的抗扰性能,本文设计了自适应RBF神经网络控制器,并对系统进行了仿真,结果显示控制器能够保证很好的控制精度,同时响应时间均在0.3 s以内,并且具有很好的抗扰动能力,满足了固冲发动机在高速工作状态下对控制效果的基本要求。反馈线性化原理的应用,克服了小扰动线性化只能保证某平衡点的控制效果的弊端,保证了自适应RBF神经网络控制器在全局内的控制效果。
