基于GM-ARIMA模型的遥测数据中长期预测

2023-07-03李志强张香燕李鸿飞田华东

计算机仿真 2023年5期

李志强,张香燕,李鸿飞,田华东

(北京空间飞行器总体设计部,北京 100094)

1 引言

卫星遥测数据是地面监视和评估卫星在轨运行状态的主要依据,它包含了各器件在轨运行的丰富信息。如果卫星器件在轨运行期间发生故障,相应的遥测数据的趋势也会发生改变。开展遥测数据长期和短期预测研究,对遥测数据的变化规律进行建模,预测未来时段的遥测数据变化趋势,就可以提前预警卫星潜在的故障,增强诊断预警系统的故障早期发现能力,为地面人员进行提前干预和处置故障提供决策依据,对保障卫星长期安全稳定运行、开展卫星长期性能研究等方面具有重要意义[1,2]。

卫星面临复杂的空间环境,影响遥测数据变化的因素具有不确定性,造成遥测数据表现出复杂的波动规律,对遥测数据的预测面临种种困难。一般地,常用的遥测数据预测方法有如曲线拟合法、小波分析法、灰色系统预测法、神经网络等方法[3-5],这些方法多适用于单调趋势的短期预报,未能充分考虑数据的季节性和随机性变化特点,对于中长期预报往往因为精度不够或者预测发散而存在缺陷。借助于时间序列分析原理,遥测数据可以分解成相应时间序列的趋势成分、波动成分,对不同成分的分别预测可能成为提高预测精度的关键。HP滤波(Hodrick-Prescott Filter)作为一种常用的时间序列数据分析工具[6,7],可以将序列分解成趋势项和波动项,已在能源、经济周期预测等多个领域广泛应用,取得了较好的应用效果。基于此,本文尝试将HP滤波应用在卫星遥测数据中长期预测中。

本文提出了一种基于HP滤波进行时间序列分解的遥测数据预测方法,即应用HP滤波法将数据分解成趋势项和波动项,分开建模、组合预测,通过叠加二者得到数据的最终预测值。该方法有别于以往把数据作为整体进行一次预测的方法,具有如下技术改进优势:1)创新性地引入HP滤波分解出趋势项和波动项,弱化了趋势、波动间的相互影响,分别进行趋势和波动的预测;2)趋势项预测采用灰色GM(1,1)模型,对单调趋势性预测效果良好,规避了灰色预测对波动性预测的不足;3)波动项采用季节型ARIMA模型,充分考虑了季节性和随机性特点,对波动性进行较好的刻画和预测。因此,该方法综合了各建模方式的优点,具有较高的预测精度,可用于数据中长期预测,为遥测参数的分析和预测、故障诊断和预警提供了一种全新的技术方法。

2 理论基础

2.1 HP滤波

HP滤波是由Hodrick和Prescot提出的一种将时间序列进行分解的方法[6]。它的基本原理是将原序列Y={y1,y2,…,yn}分为两组:趋势序列X={x1,x2,…,xn}和波动序列C={c1,c2,…,cn},其与原序列的关系如式(1)[6,7]

yt=xt+ct,t=1,2,…n

(1)

HP滤波的目的是将平滑的时间序列即趋势成分从不平滑的时间序列中分解出来,分离过程必须满足损失函数最小原则

(2)

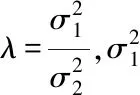
2.2 灰色预测GM(1,1)模型

GM(1,1)模型是邓聚龙教授在1982年提出的一种应用最广泛的灰色预测模型[8]。它是一种研究少数据、贫信息、不确定性问题的方法,基本思路是首先利用累加的方法使数据具备指数规律,然后建立一阶微分方程并对其求解,并将所求结果再累减还原,即为灰色预测值,从而对未来进行预测。GM(1,1)模型建模步骤如下[9,10]

设原始数据序列为X(0),X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),对X(0)作一次累加操作(1-AGO),得到序列X(1)=(x(1)(1),x(1)(2),…,x(1)(n)),其中

(3)

对X(1)作紧邻均值生成,得到均值生成序列Z(1)={z(1)(2),z(1)(3),…,z(1)(n)},其中

(4)

则GM(1,1)灰色微分方程为

x(0)(k)+az(1)(k)=b

(5)

其中a为发展系数,b为灰色作用量。

将式(3)带入式(4),得到白化的微分方程

(6)

(7)

运用最小二乘法对参数a和b进行估计,得到

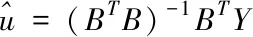
(8)

通过式(8)计算出参数a和b的值,将其代入式(7),从而可得预测模型。

最后,对预测数据经累减处理可得原始数据的预测公式

k=2,3,…,n

(9)

GM(1,1)模型常用的精度检验方法有:残差检验法和后验差检验法[10]。

1)残差检验法

残差检验是把预测数据和实际数据进行比较,检验每个点误差的大小,一般用平均相对误差作为检验标准。

原始数据序列为X(0), 根据GM(1,1)灰色模型进行预测,得到的拟合数据为(0)=((0)(1),(0)(2),…,(0)(n))。计算预测序列与原始序列的残差序列为E=X(0)-(0)=(e(1),e(2),…,e(n)),其中计算相对误差,即

(10)

GM(1,1)模型的平均相对误差即为

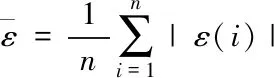
(11)

2)后验差检验法

(12)

(13)

计算的后验差比值如下

c=S2/S1

(14)

计算的小误差概率如下

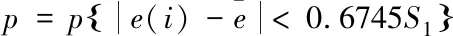
(15)

后验差检验两个比较重要的指标分别是c和p。指标c越小越好,c小就表明尽管原始数据很离散,但是经过模型后数据序列的模拟值与实际值的差并不是太离散。指标p越大越好,p越大,表明残差与残差平均值之差小于给定值0.6745S1的点较多,即拟合值(或预测值)分布比较均匀。

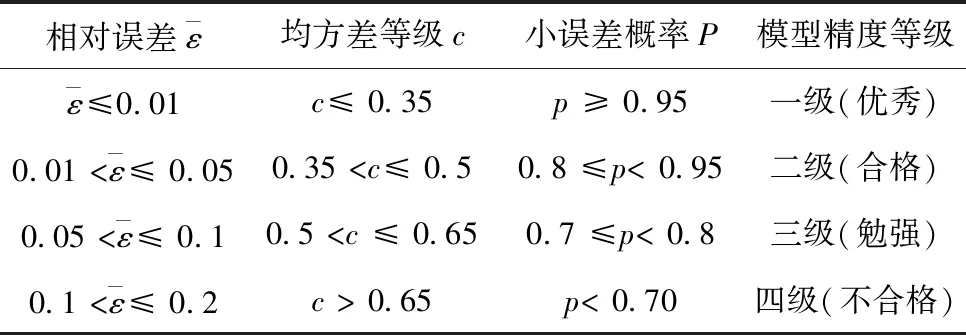
表1 模型精度等级

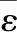
2.3 季节型ARIMA模型

单整自回归移动平均模型即ARIMA模型(AutoregressiveIntegratedMovingAverageModel),是由Box和Jenkins提出的一种时间序列预测模型[11],是一种精度较高的时间序列预测方法。

ARIMA模型的一般表达式为

Φ(L)Δdyt=Θ(L)εt

(16)

其中:εt为白噪声序列,L是滞后算子,Δdyt=(1-L)dyt是通过差分得到的平稳时间序列;Φ(L)=1-φ1L-φ2L2-…-φpLp和Θ(L)=1+θ1L+θ2L2+…+θqLq分别为自回归算子和移动平均算子多项式。

季节型单整自回归移动平均模型是以传统ARIMA模型为基础,考虑进去季节性因素调整的模型[12],即:

φp(L)ΦP(Ls)(1-L)d(1-Ls)Dyt=θq(L)ΘQ(Ls)εt

(17)

其中,φp(L)为非季节自回归算子(AR)多项式;ΦP(Ls)为季节自回归算子(SAR)多项式;θq(L)为非季节移动平均算子(MA)多项式;ΘQ(Ls)为季节移动平均算子(SMA)多项式;D、d分别为季节与非季节差分次数;P、Q、p、q分别为季节自回归、季节移动平均、非季节自回归、非季节移动平均算子的最大滞后阶数。周期为S的非平稳季节性时间序列{yt}经D次季节差分之后,即可建立季节型ARIMA(p,d,q)(P,D,Q)s模型。

建立季节型ARIMA模型有如下步骤:

1)对原序列进行平稳性检验,如果非平稳,则对序列进行差分变换,直至其平稳为止;

2)通过分析原序列或者差分序列的自相关函数(ACF)或者偏自相关函数(PACF),根据其截断和拖尾特征,确定模型的阶数,从而对ARIMA模型进行识别;

3)对模型参数进行估计,检验模型估计的残差序列是否满足随机性要求;

4)优化模型,综合比较各种模型,根据不同筛选准则,选择最优模型;

5)对未来数据进行预测,根据最小均方误差原则得到预测值。

3 建模预测方法

通过观察HP滤波后的两序列的特征,发现趋势序列X带有显著的线性趋势性,考虑建立GM(1,1)模型;对波动序列C进行相关性检验,序列C明显带有周期性和季节性,考虑建立季节型ARIMA模型。

具体步骤如下:

1)根据HP滤波,将原序列Y进行分解,得到趋势序列X与波动序列C;

2)记分解后的趋势序列X(0)=X,对序列X(0)建立GM(1,1)模型,利用最小二乘法对参数a和b进行估计,得到模型的拟合序列(0),相应的拟合公式:

(18)

其中t表示时间期数;

3)采用残差检验法和后验差检验法对GM(1,1)模型进行检验,检验模型的精度;

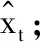
5)检验序列C的平稳性,若序列平稳则进行相关性分析,否则对序列进行差分运算直至平稳,并记为序列{wc};

6)对序列{wc}进行相关性分析,检验序列的季节性,确定模型的阶数,建立季节型ARIMA模型

(19)

8)根据HP滤波原理,得到原序列的预测结果:

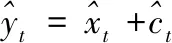
(20)

9)对模型预测结果进行误差分析,检验的误差类型为相对误差(RelativeError,RE)。

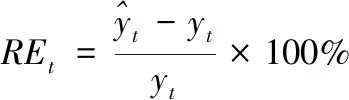
(21)

组合模型的预测流程如图1所示。组合模型预测的优势是:灰色GM(1,1)模型对近似线性指数趋势有良好的预测效果,时间序列ARIMA模型对于反映细节随机影响的波动性有良好的预测作用。故将灰色预测GM(1,1)模型和季节型ARIMA预测模型结合起来分别对趋势项和波动项进行预测,充分发挥两种预测方法的长处,有利于提高预测的精度。

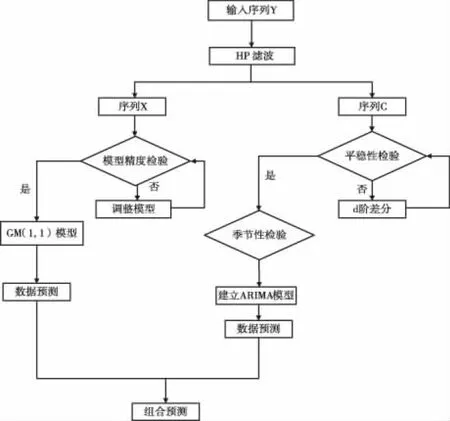
图1 基于HP滤波的组合预测流程图

4 实证分析

为了验证该预测方法,选取某卫星行波管阳压(阳极电压)2013年1月～2021年7月的在轨数据作为研究对象,其中2013年1月～2020年12月的数据作为模型识别和建模的参考数据;再用此模型预测2021年1月～2021年7月的数据,并与同期实际数据比较并计量预测误差。

阳压数据随时间变化趋势如图2所示。阳压一直有缓慢上升趋势,且每年阳压有季节性变动:这是由于随着行波管工作时间增加而出现内部电极老化衰退,表现为阳压有缓慢上升的趋势;同时又受到轨道和姿态影响,阳压还与行波管的温度环境有关,表现出一定的波峰波动性(季节性变动)。

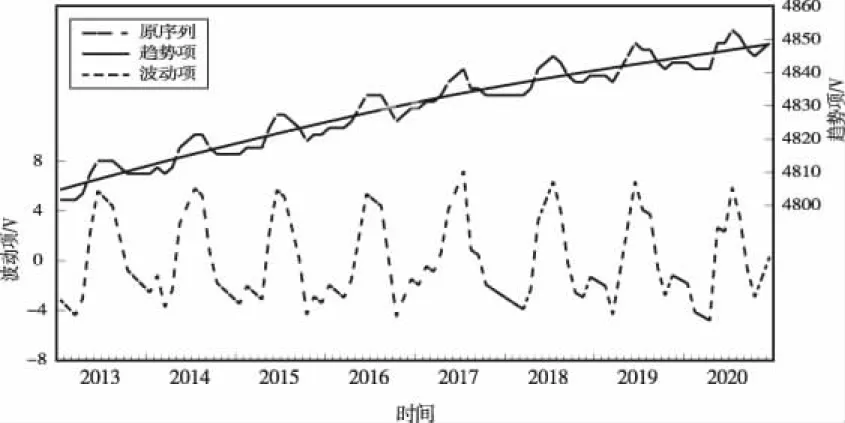
图2 HP滤波序列分解图

首先采用HP滤波法分解出趋势项和波动项。经过反复试算拟合,综合考虑趋势的光滑程度并有利于波动项建模,最终确定λ取值为14400。如图2所示,序列X曲线代表长期趋势,呈上升趋势;序列C曲线代表了季节性和周期性波动项,具有规律性变化。

4.1 趋势项预测

HP滤波分解后的趋势序列X近似一条平滑的线性曲线,对其建立GM(1,1)模型。

记初始数据序列为X(0),X(0)=(x(0)(1),x(0)(2),…,x(0)(t))=(4835.197,4835.603,…,4848.70),其中t(t=1,2,3…)为时间期数,对数据序列X(0)作一次累加运算,构造数据矩阵B以及数据向量Y,利用最小二乘法求解得到参数a=-0.0001,b=4835.3395。根据白化微分方程可得到GM(1,1)模型X(0)的时间响应式

t=2,3,…,n

(22)

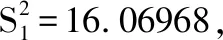
根据GM(1,1)检验结果和式(22),对2021年1月至2021年7月的序列X进行预测,得到模型的拟合和预测结果见图3,预测结果计入表3。可见,采用GM(1,1)模型对趋势项进行预测时,对整体平滑走势预测效果较好。

图3 趋势项拟合及预测值

4.2 波动项预测

为建立波动项ARIMA模型,对HP滤波后的波动序列C进行分析。为进一步消除趋势性,对序列C进行一阶差分,差分序列是平稳的,故d=1;序列C也具有季节变化规律,周期为12,为了消除季节性,进行滞后12期的季节差分处理,故D=1,S=12。

通过观察季节差分序列的PACF和ACF来进行模型的识别,可知p=12、q=4、P=0或1,Q=1。从中选择最优模型,调整后的拟合优度R2最大的是ARIMA(12,1,4)(0,1,1)12,同时其AIC值和SC值也相对较小,因此较合适的模型是ARIMA(12,1,4)(0,1,1)12。此模型估计结果见表2。

表2 模型估计结果

在模型参数估计之后,需要对模型的残差是否为白噪声过程进行检验。对模型ARIMA(12,1,4)(0,1,1)12进行拟合,图4为季节差分序列的实际值、模拟值和残差的曲线图,可见模型的模拟值与实际值的变动具有较好的一致性,残差值较小,残差比较平稳,初步判定其为白噪声过程。对残差进行ADF单位根检验后,可确定残差序列为白噪声过程。故ARIMA(12,1,4)(0,1,1)12模型为理想预测模型,可以用于预测。

图4 季节差分序列的实际值、模拟值、残差曲线图

依据该模型和式(19),对波动项2021年1月-7月的数据进行预测,得到预测结果计入表3,预测曲线见图5。可知,模型可以准确的预测随时间变化的波动性,刻画出波动特性。预测置信区间很窄,并随着预测期的扩展,预测置信区间也变大,表明越往后模型的预测精度越差。

表3 阳压预测结果

图5 波动项预测值及置信区间

4.3 组合预测及验证

依据HP滤波原理yt=xt+ct,利用上述模型进行预测,得到 2021年1月-7月的阳压预测结果并计入表3,与实际值比较,并进行可靠性验证。

由表3中可知,预测值与实际值差值非常小,相对误差都在0.04%之内,最小相对误差仅为0.0017%,如图6所示。预测结果非常准确,达到了很高的精度;在半年预测期末,预测值依然很精确。因此,模型识别及验证效果理想,在行波管状态不发生突变的情况下,可利用此模型对阳压进行较为准确的中长期预测。

图6 组合模型预测及相对误差图

阳压遥测数据的原码变化的最小单位是1个分层值,而1个分层值对应计算得到的阳压数值约为1.96,故该方法的预测精度(最大绝对误差约1.85)已经达到预测最小1个分层值的水平,精度非常高。由于阳压受空间环境、自身老化衰退等影响,基于物理规律的预测精度往往不佳。而本方法的验证结果表明,不需要考虑复杂的物理和空间因素,仅仅利用数据自身的变化规律,能够在中长期内实现优于单个分层值的高精度预测。

该组合预测方法可以推广应用于在轨故障诊断和预警中。在实际卫星的在轨管理中,利用本方法对卫星历史和实时遥测数据进行建模,可以发现理论预测值与实际值的差别,当实际值偏离预测值较大时,就可能诊断出相应设备的潜在故障状态,同时可以用来对设备远期状态进行预警。