一种重访时间约束的卫星轨道与星座设计方法

李伟建,刘旭光,刘兴威,刘裕贵

(酒泉卫星发射中心,甘肃 酒泉 732750)

1 引言

卫星轨道与星座设计是航天发射活动的基础性问题,也是航天工程应用面临的现实问题。尽管轨道设计理论和技术现已成熟,但是在面对具体应用需求时,轨道与星座设计需考虑的约束条件、影响因素等十分复杂,因此在针对不同的任务需求时,轨道与星座设计的方法仍需不断深入研究。文献[1]针对传统轨道设计方法复杂、计算量大、效率低的问题,结合遗传算法与灵敏度分析对面向区域观测任务的小卫星轨道进行优化设计。文献[2]综合考虑快速响应卫星的入轨点位置、目标的运动状态及位置属性和快响卫星的探测性能,提出了一种针对移动目标探测的快响卫星轨道设计方法。文献[3]以卫星数目最少及满足重访时间要求为优化目标,采用改进的模拟退火算法,结合改进的等面积网格点覆盖法,提出了一种针对不规则区域成像全覆盖的卫星星座构型优化设计方法。文献[4]将星座覆盖率最大化和重访时间最小化作为目标,采用遗传算法和半解析法结合的方法对轨道参数进行优化设计。本文对卫星轨道设计的理论方法和全过程进行研究,然后采用Matlab/STK联合仿真的方法实现卫星轨道设计和星座性能计算,对设计变量进行迭代搜索获得满足任务要求的设计结果,通过对星座性能参数的比较,在可行设计结果集里确定较优的设计结果,能避免复杂的算法设计,解决卫星轨道与星座设计这一复杂问题。

2 轨道设计理论方法

2.1 任务分析

卫星轨道与星座设计的目的都是为了完成某种任务,实现对地观测是大多数卫星载荷的主要功能和任务目标。以对地观测任务作为需求端,如图1所示,卫星半视场角为η,轨道高度为h,所设计的卫星轨道与星座能实现对地面目标区域每天M次的观测,最大重访时间小于T。因此,在这一任务需求下进行卫星轨道与星座设计时,需要解决两方面的问题,一是确定设计变量,二是确定重访时间这一指标的计算方法。

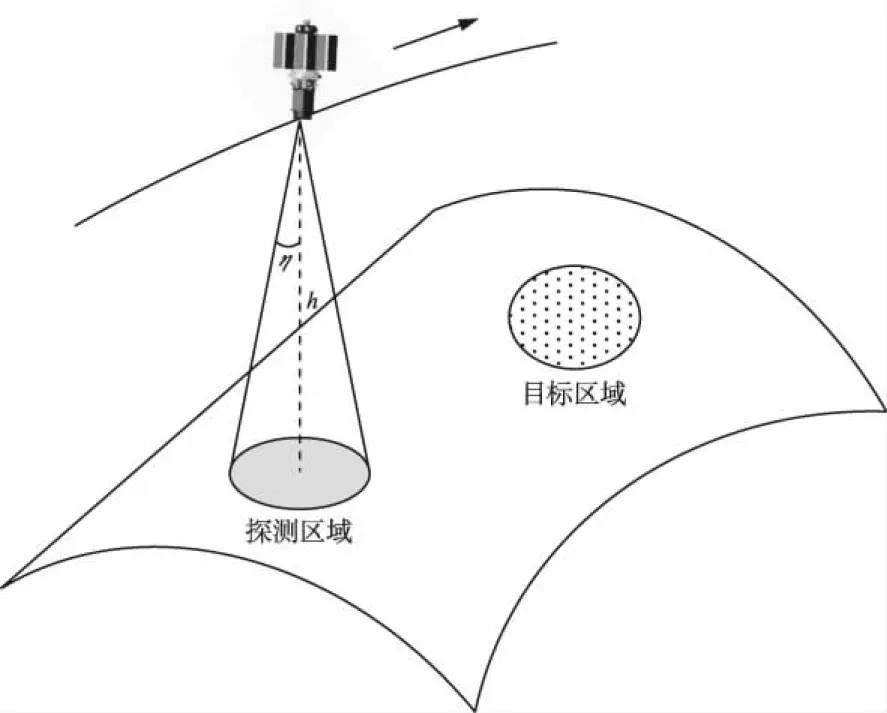
图1 对地观测任务示意图

2.2 选择设计变量

Walker星座是非常经典的星座构型,其有很好的覆盖特性和结构稳定性,已广泛应用在实际星座项目建设中。为了简化问题,选用Walker星座作为设计的起点,该星座参数包括星座中卫星总数N,轨道面数P,相位因子F。根据这组参数,在确定了一颗种子星后,既能形成整个星座。因此,设计变量从6N个变为9个,N>1。考虑到Walker星座的特点,令P=N,F=1,种子星的偏心率、升交点赤经、近地点幅角、平近点角为0,这样需要考虑的设计变量为卫星轨道高度、轨道倾角和卫星总数。

2.3 求解重访时间

为了计算重访时间,需要通过轨道外推算法、星下点轨迹计算、探测区域算法、目标区域离散化等进行联合求解,以下叙述求解过程。

2.3.1 轨道外推算法

(1)

其中,μ为地心引力常数,Re为地球平均赤道半径,J2,J3,J4为摄动模型系数,J2=-0.001082616,J3=2.53881×10-6,J4=1.65597×10-6。计算赤道惯性坐标系下位函数的梯度,可以得到航天器在赤道惯性直角坐标系下的摄动加速度分量,将其叠加到二体模型,从而可以得到考虑J4引力摄动的轨道递推模型为

(2)

2.3.2 星下点轨迹

考虑地球旋转时,t时刻的星下点可用其地心纬度、经度(φ,λ)描述如下

φ=arcsin(sinisinu)

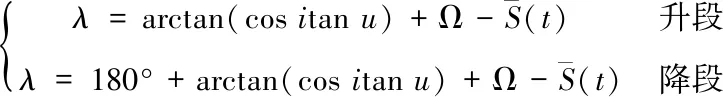
(3)

(4)

(5)

式(5)中,JD(t)为计算时刻t对应的儒略日。

2.3.3 探测区域算法

(6)

式(6)中,dσ对地覆盖角,乘以地球半径Re就是覆盖区域半径,η为卫星半视场角,h为卫星轨道高度。

2.3.4 目标区域离散化

以圆形区域为例,给出圆形区域的离散化方法,如图2。

图2 目标区域离散化示意图

假设目标区域为以O1为圆心,R为半径的圆形区域,先将区域(φmin,φmax)×(λmin,λmax)划分为m×n的点阵,对于点阵中的任意点P,其坐标为(φi,λj),目标区域包含的离散点可由下式确定

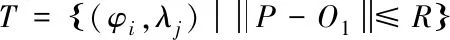
(7)

2.3.5 重访时间计算

根据卫星载荷性能参数,联合式(2)～(7)进行计算,可以确定当前时刻点卫星对地覆盖情况,如图3所示。设O2、O3为连续两次探测到目标区域,记O2探测到目标区域的起始时间为t1,O3探测到目标区域的起始时间为t2,则重访时间为|t2-t1|。

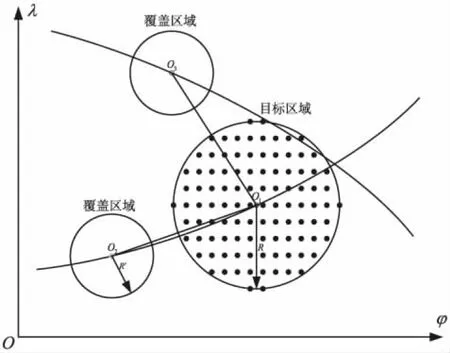
图3 卫星对地覆盖区域示意图

通过比较卫星覆盖区域与目标区域是否相交来确定目标区域被发现的起始时间和时长。确定t1的条件为

(8)

同样可得确定t2的条件为

(9)

3 基于Matlab/STK的星座设计仿真实现

Matlab与STK的联合仿真为航天任务设计与分析提供了非常便利快捷的分析手段,也使得星座设计[6,7]与星座性能分析[8]变得简单、直观。第2节中轨道设计的理论方法编程实现较为困难,而利用Matlab/STK联合编程实现就相对容易。下面说明上述理论方法通过Matlab/STK联合仿真的具体实现过程,见图4。

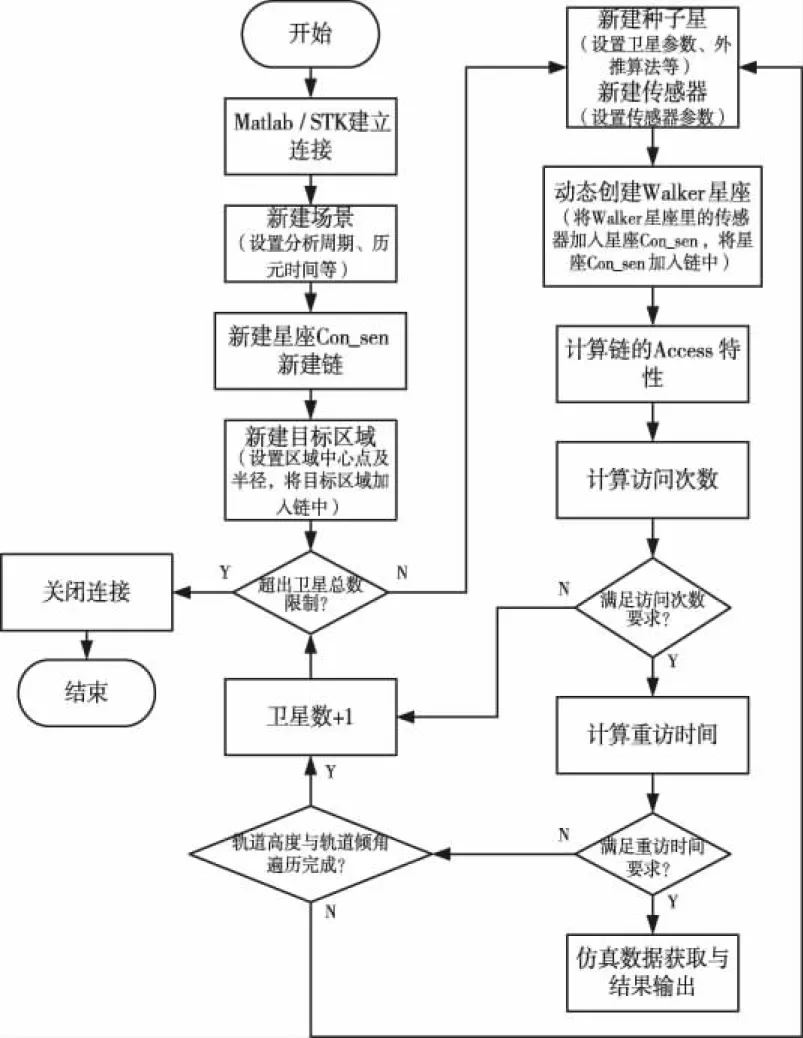
图4 星座设计Matlab/STK联合编程实现

4 设计结果分析

以观测某区域为例进行卫星轨道和星座设计,设计时用到的初始条件如表1所示。下面对设计结果进行分析。

表1 初始条件值

根据表1提供的初始条件,运用图4中的编程算法,可以对这个观测任务进行轨道和星座设计和分析。图5为轨道倾角为45°时,不同卫星数量情况下,重访时间随轨道高度的变化曲线。从图可以看出,在不同卫星数量情况下,重访时间与轨道高度间关系复杂,无章可循,在各轨道高度下,重访时间随着卫星数量增加而减小。但需指出的是,当卫星数量为8颗时,在给定的上下限范围内没有符合要求的轨道高度使重访时间满足要求。

图5 轨道倾角为45°时,重访时间随轨道高度的变化曲线

图6为轨道高度480km时,重访时间随轨道倾角的变化曲线,从图可以看出,在卫星数量确定的情况下,重访时间随轨道倾角的变化也相当复杂,在卫星数为6颗时,轨道倾角为50°时,重访时间不满足要求。而在轨道倾角一定时,重访时间也不是严格随卫星数量增加而减小。

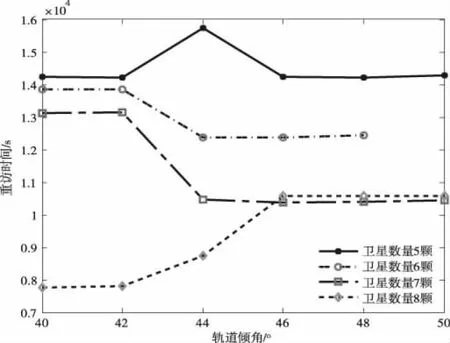
图6 轨道高度480km时,重访时间随轨道倾角的变化曲线

轨道高度步长取为20,轨道倾角步长取为2,进行迭代搜索,获得了296个能满足访问次数与重访时间要求的可行设计结果,表2给出了不同卫星总数情况下重访时间最小的设计结果。

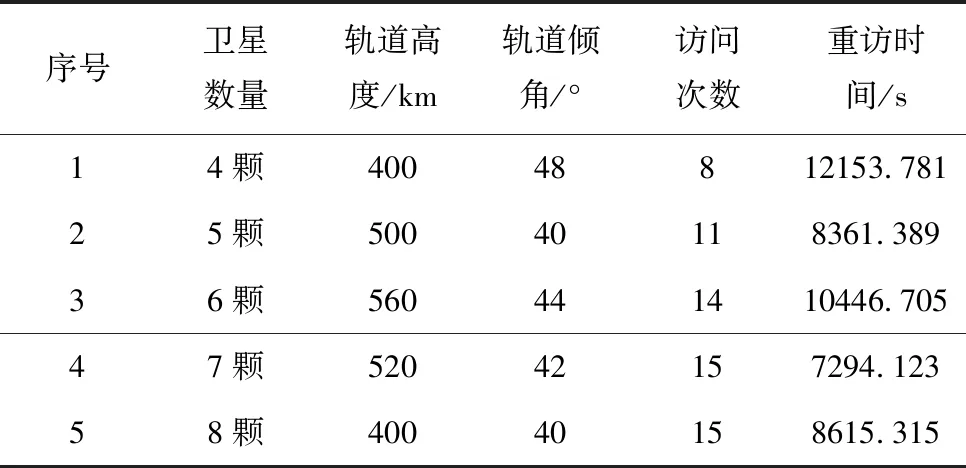
表2 不同卫星总数情况下重访时间最小的设计结果

从表2可以看出,如果要求卫星数量最少,则第一组参数为较优的设计结果,如果要求重访时间最小时,则第4组参数为较优的设计结果。

5 结论

从文中设计结果分析可看出,星座设计变量与星座性能参数间往往具有非常复杂的关系,因此为了完成特定任务的卫星轨道和星座设计是一个非常复杂的问题。本文提出的轨道设计理论方法是卫星轨道与星座设计的一个整体框架,只要任务目标函数能够进行求解,都能运用这一框架进行卫星轨道和星座设计,而通过基于Matlab/STK的联合编程实现,能够使这一设计问题的求解变得简单与直观。