基于等维递补灰色模型的深基坑地表沉降预测*

丁玉贤,任聚阳,郝林

(1.内蒙古科技大学 土木工程学院,内蒙古 包头 014010;2.内蒙古自治区高校智能建造与运维工程研究中心,内蒙古 包头 014010;3.兴泰建设集团有限公司,内蒙古 鄂尔多斯 017000)

随着我国城市化进程的加快,现有的地上空间已经不能满足人们的需求,人们逐渐将建设项目的空间向地下扩展,我国已成为地下空间开发利用的名副其实大国[1].在深基坑工程施工中,必须保证自身及周边环境的安全.但是由于地下工程往往施工工期长,趋于最终稳定的时间长,因此对基坑支护结构自身及周边环境状况进行全方位、持续性监测,显得尤为重要[2].在深基坑沉降监测的诸多因素中,地表沉降问题对周边环境带来的的破坏很大,是深基坑工程监测的重要组成部分[3].因此,如何及时有效地利用监测数据进行深基坑地面沉降预测,已成为地下空间工程的技术难点和热点.

深基坑沉降预测常用的数学模型有:回归分析模型、时间序列模型、神经网络模型[4]以及灰色理论模型[5].其中,灰色GM(1,1)模型具有所需数据信息少、模型建立简单和求解简单等特点,在沉降变形预测中应用最为广泛[6].但它也有一些缺点,如对原始数据序列的要求相当严格.针对它的缺点,近年来许多学者对GM(1,1)模型进行了改进.翁志坚等[7]建立了马尔科夫优化的GM(1,1)模型,精确预测了随机波动较大的沉降变形;王炳等[8]提出了非等间距线性时变参数GM(1,1)幂模型,在小、非等距样本以及短期预测分析方面具有优势;钟立华等[9]利用残差修正法与马尔可夫法对灰色模型进行了改进,实现了预测系统的总体设计.

但是上述方法都没有解决未来时间越长,预测区间越大,模型预测结果逐渐失真的问题.等维递补GM(1,1)模型不仅继承了传统静态灰色模型的优点,而且及时考虑了不断影响系统的因素,以优化和改进动态预测[10].因此,等维递补灰色模型是最理想的动态预测模型.针对这种情况,研究采用实测数据分析法[11],建立等维递补灰色GM(1,1)模型,以郑州市东风路地铁车站深基坑工程为例,对深基坑地表沉降预测进行了实验,取得了良好效果.

1 传统灰色GM(1,1)模型

1.1 数据的检验与处理

在建立灰色预测模型之前,必须检验该建模方法的适用性.设原始数据为x(0)=(x(0)(1),x(0)(2),…,x(0)(n)),计算序列级比;如果所求级比在可容性覆盖区间内,则该序列x(0)能够适用灰色预测模型,否则就要平移变换处理该组原始数据,使作平移变换后的数据的级比落入允许覆盖区间内.

1.2 建立模型

1.2.1累加序列的生成

对原始数据序列(非负序列),作一次累加运算得到新的一阶累加序列公式(1),即1-AGO序列.

(1)

1.2.2加权邻值序列的生成

对一阶累加序列x(1)(k)按照式(2)生成紧邻均值序列z(1)(k).

(2)

1.2.3建立灰微分方程

结合原始序列数值和紧邻均值序列数值,根据式(3)建立灰微分方程.

x(0)(k)+az(1)(k)=b,k=2,3,…,n.

(3)

式(3)中:a为发展系数;b为灰色作用量.

1.2.4建立预测模型

将所求参数代入式(4)进行求解,可得预测模型.

(4)

经过累减还原生成预测值,用式(5)表示为:

(5)

1.3 精度检验

通过灰色GM(1,1)模型得到预测数据结果同时,还要检验该模型精度准确性.依据后验方差比值C和小误差概率P值分为4个等级[12],等级的具体分类如表1所示.后验差比值C越小,小误差概率P越大,模型越稳定、越精确.

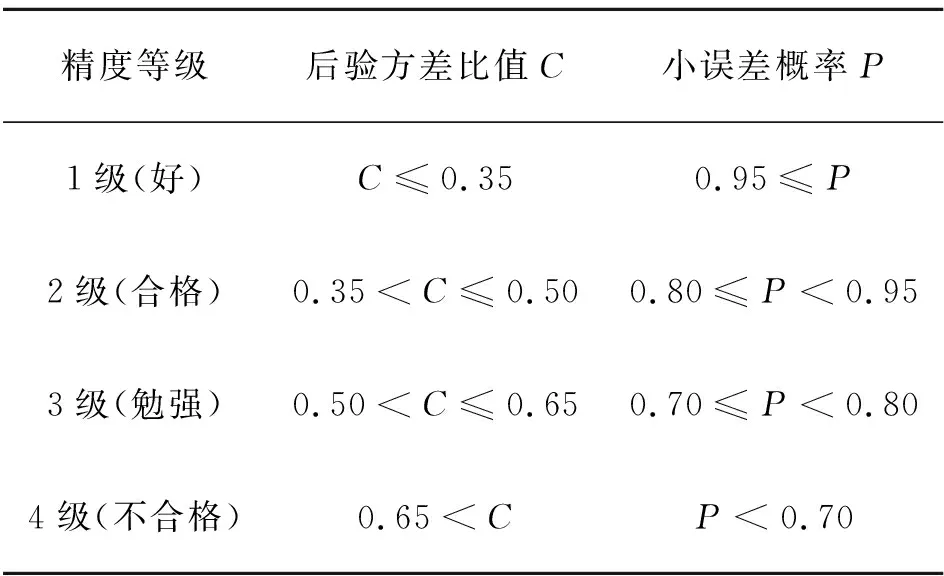
表1 模型精度检验等级分类

2 等维递补模型建模

2.1 模型建立思路

当使用等维递补灰色模型进行动态预测时,首先用原始数据序列建立GM(1,1)灰色模型以预测下一个值,然后将预测值添加到已知数值序列中,同时去除掉最原始的数据以保持序列维度不变,接着再建立GM(1,1)模型进行预测.通过这种方式,灰数不断引入新信息,去除老化信息,并逐一进行预测,直到完成目标预测.

2.2 模型建立步骤

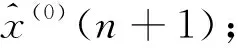
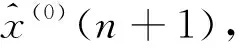
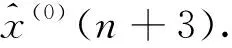
3 实例分析

3.1 工程概况

东风路站为郑州市轨道交通8号线的第十一座车站,车站主体结构外包长度为243 m,标准段宽22.1 m,站台宽13 m,设有5个出入口,4个风亭组,1个换乘通道.车站采用明挖法施工,基坑开挖受站位、场地大小等因素的影响,易发生偏载现象,基坑周边荷载严重失衡时会导致整个基坑出现大的沉降.因此,基坑的沉降监测及预测工作就显得尤为重要.

3.2 建模与预测

以该地铁站深基坑周围岩土体地表沉降观测作为研究样本,前期监测发现DBC-16-02点位沉降累计达14.71 mm,为该时间沉降累积量最大值,故选取针对地表沉降观测点DBC-16-02的9个观测周期(即2021年11月12日～2021年11月20日)的观测数据进行建模.以11月12日～20日的观测数据为原始数据,运用SPSS数据统计分析软件,对11月21日及之后的沉降数据进行预测.

3.2.1级比检验

将原始数据导入SPSS数据统计分析软件,首先进行级比检验.结果显示,所有级比值均位于区间(0.819,1.221)内,也就是都在可容许覆盖区间内,说明原始数据序列适合构建灰色预测模型.

3.2.2采用传统静态预测模型建模

继续采用SPSS数据统计分析软件,得出a和b等参数,代入式(4)和式(5)计算出该工程的时间响应式,用公式(6)表示:

(6)

进行精度检验,DBC-16-02点位后验差检验指标C=0.297<0.35,小误差概率P=0.778<0.80;故该模型精度为三级.

3.2.3建立等维递补GM(1,1)模型

该研究构建了六次等维递补GM(1,1)模型,发现精度随着递补次数增多,先是升高后又降低.为了凸显传统静态GM(1,1)模型和等维递补修正模型的差异,这里展示前三次的递补结果.

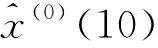
(7)

2)二次递补预测模型用公式(8)表示为:

(8)

3)三次递补预测模型用公式(9)表示为:

(9)

根据表2,传统静态GM(1,1)模型小误差概率0.778,后验方差比值0.297,故该模型为三级精度模型,可进行基坑沉降预测,但适用于短期预测.通过一次递补的GM(1,1)模型小误差概率0.889,后验方差比值0.165,模型精度为二级;二次递补优化和三次递补优化的等维递补模型,其小误差概率和后验方差比值结果显示,精度可达一级.综上所述,研究提出的改进模型较传统静态模型,其后验方差比值指标和小误差概率指标都有所提升.

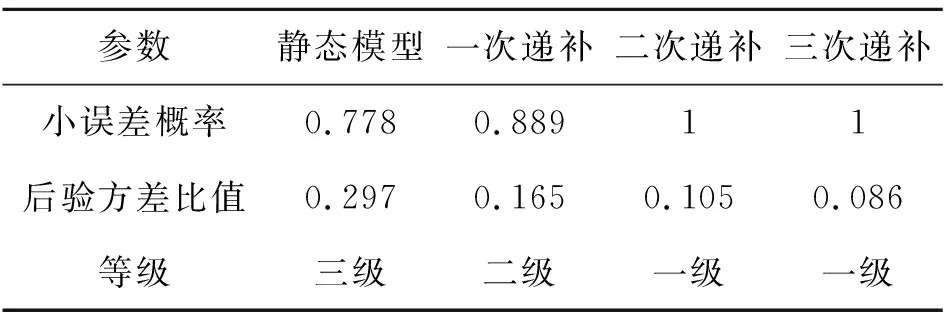
表2 预测模型精度对比表

基于静态GM(1,1)模型和等维递补GM(1,1)模型对该工程11月21日～23日的地表沉降累计值进行了预测,见表3和图1.

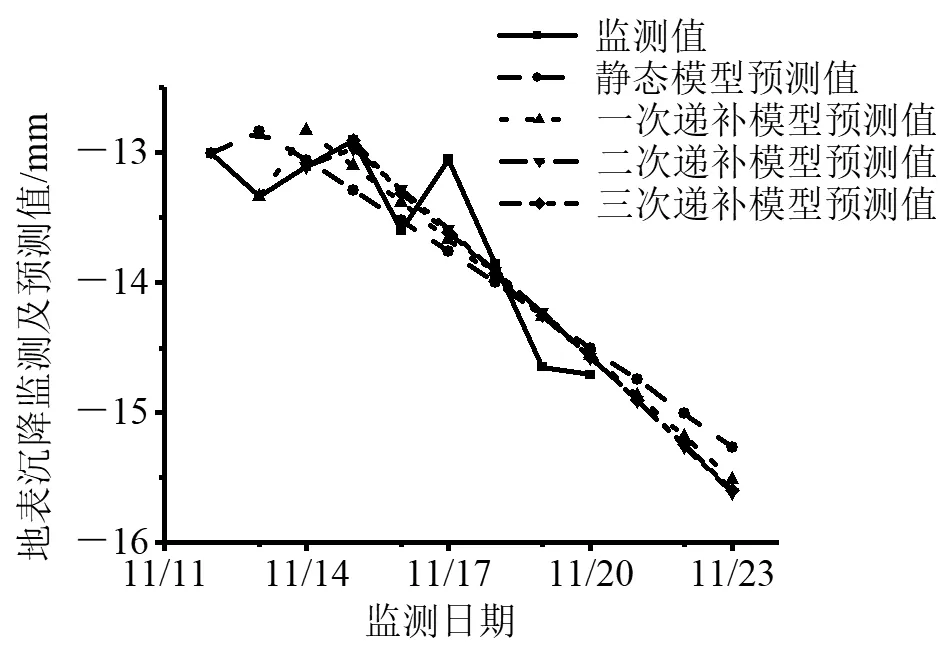
图1 地表沉降数据统计及预测

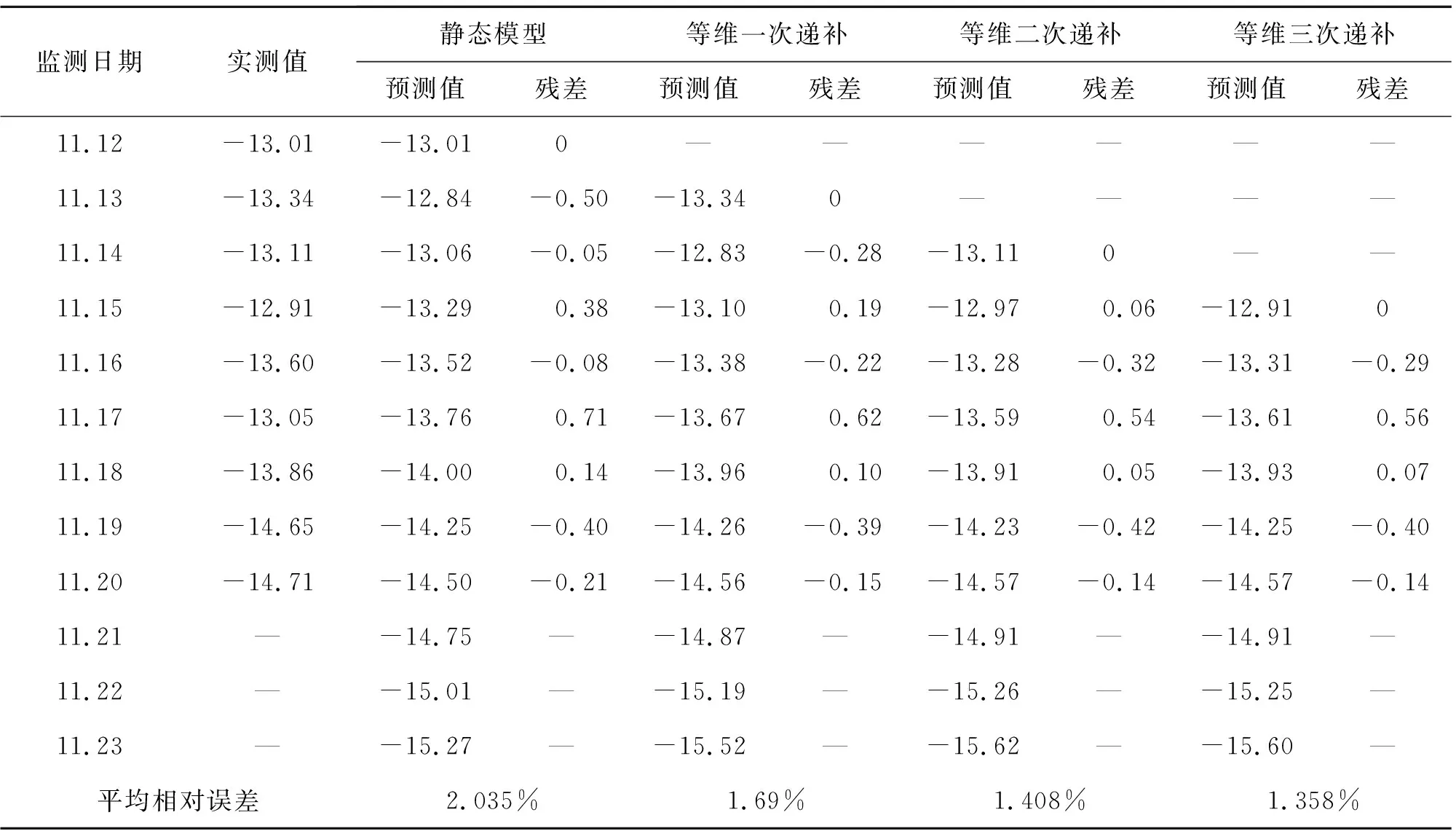
表3 郑州市东风路站DBC-16-02点位地表沉降监测及预测数据统计(累计沉降值,mm)

从表3可得出,传统静态GM(1,1)模型经过递补修正,平均相对误差逐渐减小,这也与表2结论一致;图1中可以看出,除14日、15日和17日受外力支撑作用,现场地表出现隆起外,其余曲线走势一致,并且随着预测期数增加,递补模型较静态模型预测数值更加接近真实值.11月20日三次递补模型较静态模型预测与实测偏差小7 mm.同时,图1中还可得出,地表沉降累计值仍在递增当中,根据《城市轨道交通工程监测技术规范》,地表沉降累计控制值24 mm,变化速率10 mm/d,因此目前处于安全可控状态.未来施工中,要加强沉降监测以及做好提前预测,直至预测曲线出现平缓.

4 结论

1)与传统的静态灰色预测模型相比,等维灰数递补修正模型平均相对误差小,模型精度高,更适合沉降预测.对于信息相对有限的地表沉降预测,等维递补修正模型具有更可靠的实用价值和广阔的应用前景;

2)等维递补灰色模型随着递补次数逐渐增多,原始数据逐渐减少,模型精度呈现先增大后减小趋势.因此,递补次数不宜过多,一般以2～3次为宜;

3)持续监测和预测显示,该工程地表沉降监测值和预测值累计均在20 mm以内,低于28 mm预警值,安全可靠.