外肋板刚度对外肋板式组合剪力墙结构抗震性能影响研究*

郝林峰,万馨,刘一

(内蒙古科技大学 土木工程学院,内蒙古 包头 014010)

剪力墙作为建筑中的关键抗震构件,自钢板混凝土组合剪力墙提出以来,国内学者对其进行了大量的研究.聂建国[1,2]团队、李云等[3]、李奉阁等[4]对多种钢板组合剪力墙进行试验分析,发现此种剪力墙承载力高,抗震性能好,具有较好的应用前景.

将双钢板混凝土组合剪力墙与钢梁组合,通过外肋板与外伸梁段加强节点连接,形成一种新型的墙梁结构.前期研究结果表明,该结构承载力及抗震性能较好,具有一定的实际应用价值[5].但结构的节点外肋板易发生开裂,影响结构性能.而针对节点板件的研究较少,没有相关的设计参考.本文运用ABAQUS软件进行有限元模拟,分析不同钢材屈服强度和钢连梁变形特征下,外肋板宽厚比对结构抗震性能的影响.探究外肋板最佳尺寸,以提供相关设计建议,指导工程实践.

1 有限元模型确立

图1为外肋板式联肢钢板组合剪力墙—钢梁结构形式.外伸梁段与剪力墙焊接,外肋板通过焊接连接剪力墙与外伸梁段翼缘以加强节点.外伸梁段与钢连梁的连接中,翼缘为焊接,腹板为螺栓连接.剪力墙呈矩形,由外包钢板与内筑混凝土构成,外包钢板间焊接加劲肋以提高钢板与混凝土的协同工作性能.

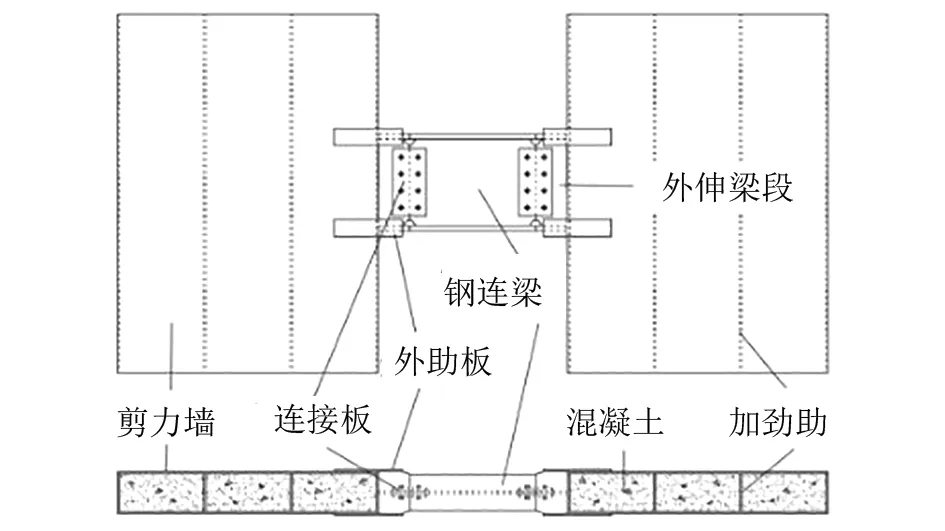
图1 外肋板式联肢钢板组合剪力墙—钢梁结构形式

1.1 模型参数

本文研究对象为3层的外肋板式联肢钢板组合剪力墙—钢梁结构.层高3 m,顶部预留0.2 m设置加载梁,总高度9.2 m.剪力墙宽0.8 m,厚0.2 m.

钢材本构关系采用Von Mises屈服准则和硬化弹塑性模型.弹性模量E=2.06×105MPa,强化段的模量取弹性模量的1%[6],泊松比为0.3.螺栓采用10.9级M27高强度螺栓,螺栓钢材本构取自文献[5],弹性模量E=2.11×105MPa.混凝土为C40混凝土,本构关系采用塑性损伤模型,弹性模量E=3.25×104MPa,泊松比取0.2[7].

高强螺栓采用B31单元,钢构件及混凝土采用C3D8R单元.模型墙底部固定,墙顶施加侧向约束.构件焊接采用绑定约束模拟,钢连梁腹板与连接板之间、混凝土与钢板之间定义接触,摩擦系数取0.35.对墙顶施加轴向荷载,同时设置加载梁保证加力均匀.加载模型如图2所示.

图2 加载模型

图3为模型的加载制度,采用位移控制分级加载,其中Δy为屈服位移.将墙顶加载梁以加载点为控制点设置刚体,加载位移施加于加载点上.屈服前位移荷载分3级,每级递增0.25Δy反复一次.结构达到屈服以后,每级递增0.5Δy反复2次,试件的荷载下降到峰值荷载的85%时停止加载[8].

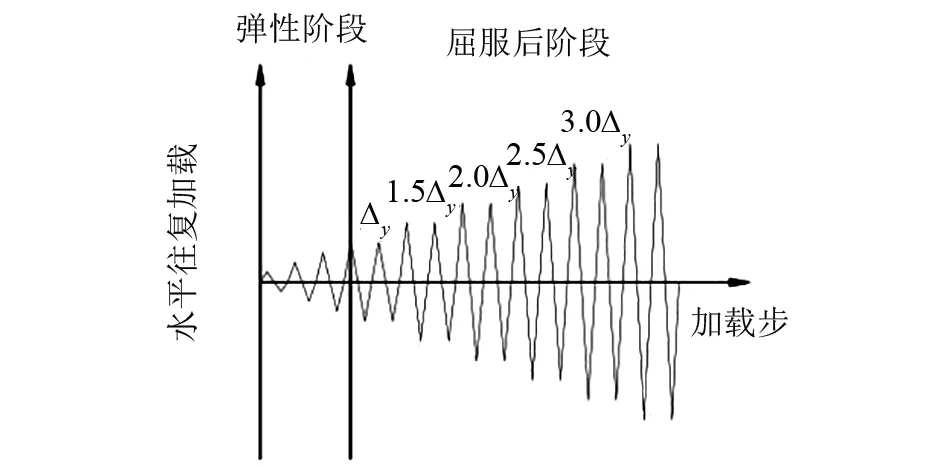
图3 加载制度

1.2 有限元模型验证

为验证上述模拟方法与实际试验是否相符,对文献[9]中的试件进行模拟验证,建模方法及各参数均与上述相同.试件为型钢混凝土组合剪力墙-钢连梁结构.试件共5层,由型钢框架、钢板、混凝土组成.试件经过1/4缩尺,层高0.8 m,剪力墙宽0.8 m,厚0.12 m.钢框架为90 mm×60 mm×6 mm×10 mm的H型钢焊接而成,内含6 mm钢板.钢梁一、二层为150 mm×130 mm×6 mm×10mm,三、四、五层为160 mm×100 mm×6 mm×10mm.剪力墙顶部设置加载梁,底部设置基座梁.

试件在加载过程中,混凝土裂缝首先出现在底层.之后裂缝由下至上,由外向内逐渐发展.当加载位移到40 mm时,一、二、三层的钢连梁出现剪切变形.加载后期,墙底角部的混凝土大面积压溃脱落,混凝土脱落部位的钢筋和型钢柱露出.其中暗柱的外侧纵筋被拉断,中部纵筋被压弯.图4为钢框架、钢筋和第二层钢连梁的模拟结果与试验结果的对比,模拟结果与试验结果符合程度较好.

图4 试验和模拟破坏现象对比

图5为试件滞回曲线和骨架曲线的对比.两者滞回曲线形状大致相同,有限元滞回曲线比试验滞回曲线更加饱满.骨架曲线中,加载中期的2曲线有些许偏差,峰值点位移有限元延后10.2 mm,屈服荷载有限元比试验大9.8%左右.由于有限元软件不能模拟出混凝土的开裂对结果的影响,以及试验试件的材料本身、试件制作及加载过程的各项缺陷等的影响,使模拟结果与试验结果出现差异.但两者结果差异较小,数据差异在10%以内.

图5 滞回曲线与骨架曲线对比

1.3 有限元模型拓展设计

表1为模型设计参数,模型编号中,S代表剪切型,BS代表弯剪型,B代表弯曲型;r+数字代表外肋板宽厚比数值.为排除耦连比的影响,模型耦连比均设计为0.45.钢连梁变形特征在限制相同的Mp/Vp(Mp为钢梁的塑性受弯承载力,Vp为钢梁的塑性受剪承载力),通过不同的钢连梁跨度来改变[10].其中剪切型表示钢连梁以剪切变形为主;弯剪型表示钢连梁变形介于剪切变形和弯曲变形之间;弯曲型表示钢连梁以弯曲变形为主.钢连梁截面尺寸在满足上述条件的情况下选取.

表1 模型设计参数

1.4 外肋板测点选取

图6为文献[5]试验试件的外肋板破坏图.在外肋板上选取合适测点,测量加载过程中测点区域的应力变化,确定外肋板是否能在各构件破坏前稳定传力而不发生破坏.测点应设置在外肋板易发生破坏的位置,即外肋板的薄弱部位.图中外肋板的外侧(与外伸梁段腹板不处于同一平面的一侧为外侧)在外伸梁段与剪力墙连接界面处发生断裂.

图6 外肋板破坏图

图7为模型节点的应力云图,图中外肋板在外伸梁段与剪力墙连接界面处的外侧应力较高.由此可以判断,外伸梁段与剪力墙连接界面的外侧为外肋板的薄弱部位,测点将选取模型第二层连接外伸梁段上翼缘与加载侧剪力墙外肋板的薄弱部位.

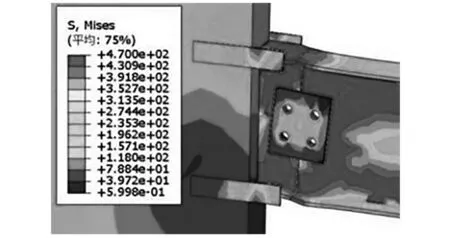
图7 节点应力云图

2 有限元结果分析

2.1 不同钢材屈服强度下外肋板宽厚比对结构抗震性能的影响

1)对结构抗震性能的影响

图8为3组不同钢材屈服强度模型的骨架曲线,表2为各模型的位移延性系数和能量耗散系数,其中各参数按照规程[11]进行计算.结果表明,增大外肋板宽厚比可略微提高结构的承载力.外肋板宽厚比由4提高到12,结构延性和耗能略有提高.同时过高的宽厚比会使外肋板变薄,外肋板刚度减弱,降低节点的稳定承载能力.因此,外肋板宽厚比为16和20的模型延性和耗能出现下降.

表2 各模型的位移延性系数和能量耗散系数

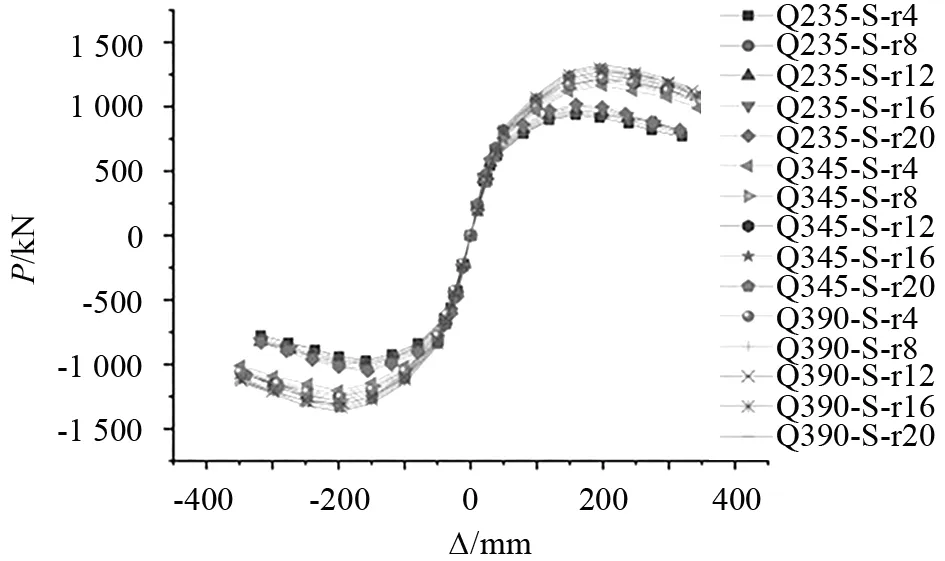
图8 骨架曲线

2)外肋板受力分析

图9为3组模型外肋板的受力变化曲线.图中Δy为结构达到屈服时对应的屈服位移,Δmax为结构达到极限承载力时对应的位移.分析3组数据可得到初步结论:在相同的结构及加载条件下,选取不同的外肋板宽厚比使外肋板上的应力产生较大差异.3组数据中,外肋板宽厚比为12的模型,其外肋板上的应力最小.在结构达到屈服时,外肋板上的应力未达到钢材的屈服强度;所施加荷载达到结构极限承载力时,外肋板上的应力未达到钢材的抗拉强度.这保证了外肋板传力的可靠性,避免节点先于各构件发生破坏.

图9 外肋板受力变化曲线(a)Q235-S系列;(b)Q345-S系列;(c)Q390-S系列

通过对3组数据逐一分析发现,当采用Q235钢材时,外肋板宽厚比为4,8,16,20的模型,外肋板上的应力在结构屈服前达到钢材的屈服强度;采用Q345钢材时,外肋板宽厚比为4,16,20的模型,外肋板上的应力在结构屈服前达到钢材的屈服强度;采用Q390钢材时,外肋板宽厚比为16,20的模型,外肋板上的应力在结构屈服前达到钢材的屈服强度.因此,外肋板宽厚比不宜选取过高,其次在选材时应优先选用高强度钢材.

2.2 不同钢连梁破坏特征下外肋板宽厚比对结构抗震性能影响

1)对结构抗震性能的影响

图10为3组不同钢连梁破坏特征模型的骨架曲线,表3为各模型的位移延性系数和能量耗散系数.通过分析各组数据发现,提高外肋板宽厚比对结构抗震性能的影响与前三组分析的规律基本一致.外肋板宽厚比的增大,可略微提高结构的承载力;延性和耗能随着外肋板宽厚比的增大,呈先提高后下降的趋势.

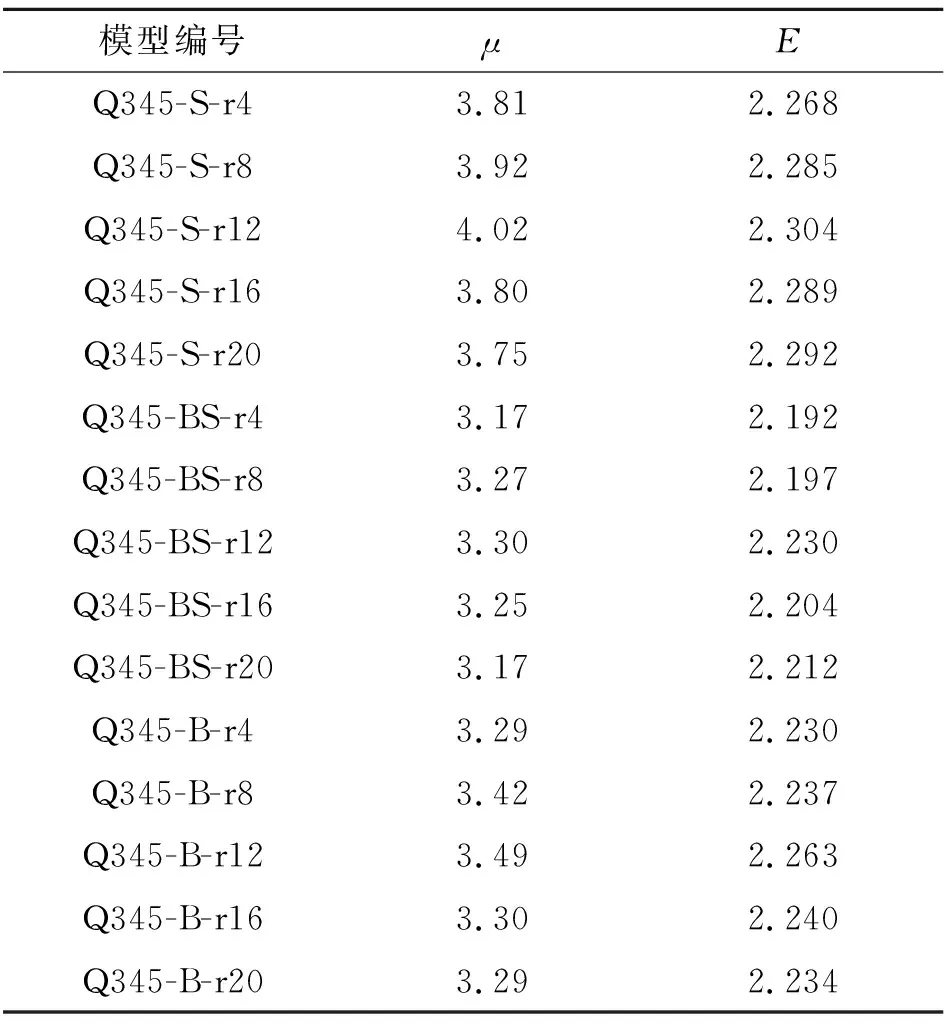
表3 各模型的位移延性系数和能量耗散系数

图10 骨架曲线

2)外肋板受力分析

图11为3组模型外肋板的受力变化曲线.通过分析发现钢连梁变形特征对外肋板宽厚比的取值影响较小,3组模型的曲线分布都符合Q345钢外肋板宽厚比取值的结论.

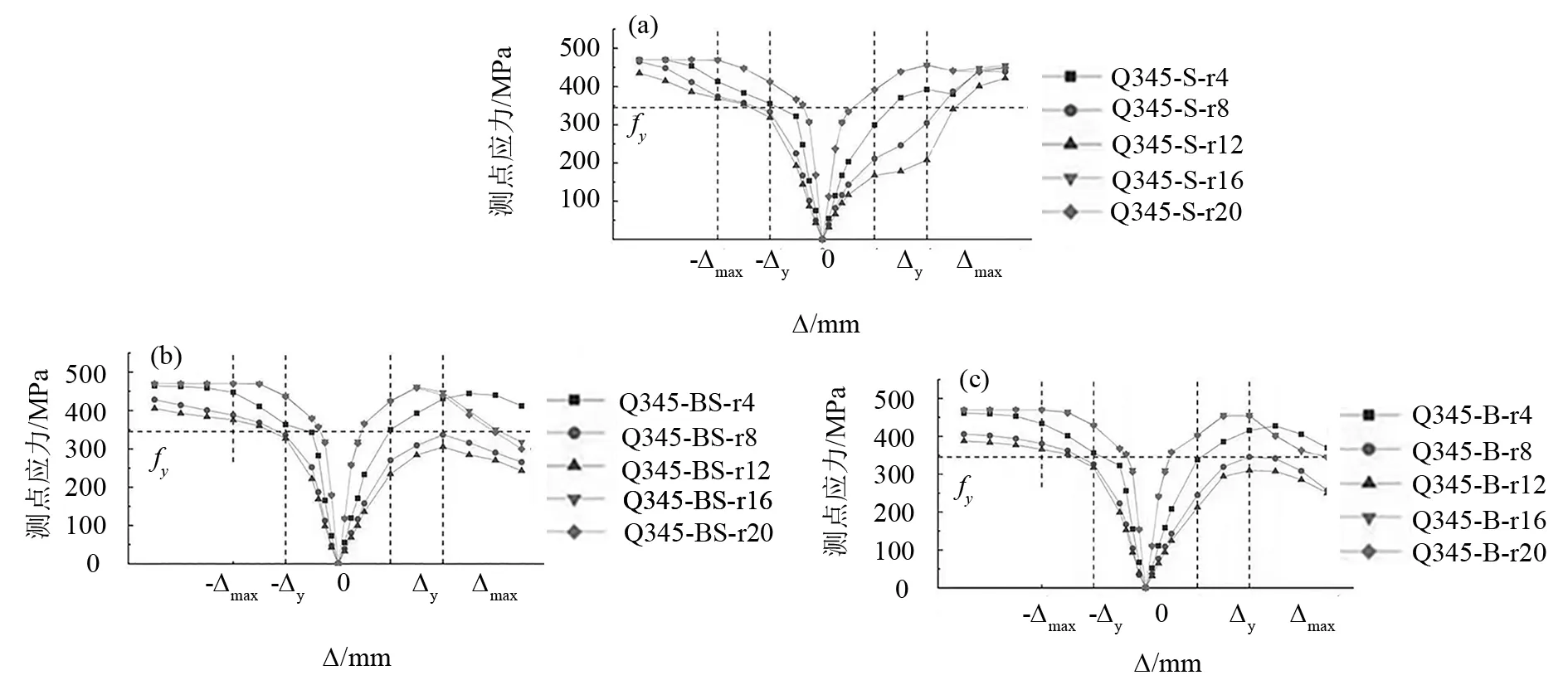
图11 外肋板受力变化曲线(a)Q345-S系列;(b)Q345-BS系列;(c)Q345-B系列

3组模型的曲线的差异主要体现在正向加载中结构屈服后的阶段.弯剪型和弯曲型2组模型的外肋板在结构达到极限承载力后,测点上的应力出现下降.这是由于相同耦连比下,弯剪型和弯曲型结构的节点需传递比剪切型更大的弯矩,外肋板测点区的钢材在加载中发生较大变形,承载力降低.因此,弯剪型和弯曲型的结构需要更大尺寸的外肋板以抵御变形.

综上分析发现,合理设置外肋板尺寸能够在保证结构性能的情况下,减小外肋板薄弱区域的应力.这将大大降低外肋板开裂的风险,保证节点稳定传力.实际工程中,可参考本文结论确定外肋板尺寸.

3 结论

1)综合分析五组模型数据发现,当外肋板宽厚比为12时,外肋板上应力最小.因此外肋板式联肢钢板组合剪力墙—钢梁结构的外肋板宽厚比取值以12最佳.

2)选取高屈服强度的钢材可放宽外肋板宽厚比的取值范围:当外肋板采用Q235钢时,外肋板宽厚比应控制在12左右;当外肋板采用Q345钢时,外肋板宽厚比可选取在8～12范围内;当外肋板采用Q390钢时,外肋板宽厚比可选取在4～12范围内.

3)钢连梁的变形特征对外肋板宽厚比的取值影响较小,仍以12为最佳取值,但弯剪型和弯曲型的结构需要较剪切型更大的外肋板尺寸,以保证节点的可靠性.