可调谐液晶双折射滤光器的原位定标方法（特邀）

侯俊峰，孙英姿，林佳本，张洋，王东光，邓元勇，张志勇

（1 中国科学院国家天文台， 北京 100101）（2 中国科学院大学 天文与空间科学学院， 北京 100049）

0 引言

太阳是一个巨大的等离子实验室，其间的一切现象和过程都是电磁相互作用引起的，因此太阳磁场的观测研究在当代太阳物理学和空间天气学中占有举足轻重的地位。目前成熟的太阳磁场测量方法主要是基于Zeeman 效应开展的［1］。太阳物理学家们通过太阳望远镜测量夫琅和费磁敏谱线经过Zeeman 效应后偏振光的Stokes 参量变化，再利用太阳大气的辐射转移模型反演获得太阳磁场的信息［2］。因此，太阳望远镜的磁场测量本质上是窄带偏振测量。对于成像型设备而言，太阳磁场测量要求滤光带宽一般在0.01 nm 左右，高精度、高灵敏度的窄带调谐成像是太阳望远镜能否实现精确磁场观测的核心技术之一［3］。

Lyot 双折射滤光器是由LYOT B 于1933年发明的一种成像型滤光设备，通过高双折射晶体的干涉效应实现超窄带滤光，是太阳望远镜最常用的窄带成像设备［4-6］。传统的双折射滤光器采用旋转波片的方法调节透过的中心波长，然而机械调制不仅速度慢，而且应用于空间望远镜时面临寿命、气泡、漏油等可靠性风险。基于此，近些年随着液晶调制技术［7］的迅猛发展，可调谐液晶双折射滤光器逐渐受到青睐，其采用向列液晶可变延迟器（Liquid Crystal Variable Retarder， LCVR）取代机械调制实现透过波长调节，速度快且不存在气泡、漏油等风险，显著提高了滤光器的科学性能和可靠性［8-10］。

自2014年以来，中国科学院国家天文台侯俊峰等在LCVR 以及可调谐液晶双折射滤光器方面进行了深入的研究，逐步解决了LCVR 的光学质量、相位稳定性、干涉效应、空间适应性等问题［11-15］，相关技术已应用于中国科学院空间科学战略性先导科技专项二期卫星型号项目先进天基太阳天文台（Advanced Spacebased Solar Observatory，ASO-S）［16］，而且目前研制的可调谐液晶双折射滤光器也已应用于国家重大科技基础设施“子午二期工程”的全日面矢量磁像仪。

尽管如此，由于LCVR 属于液晶型电光调制器，当可调谐液晶双折射滤光器面向空间望远镜应用时，受辐照、力、热、充电效应等综合因素影响，LCVR 的相位延迟-电压曲线存在漂移风险，可能导致滤光器的透过轮廓发散以及中心波长漂移，从而降低了滤光器的测量精度。因此，如何实现可调谐液晶双折射滤光器的原位定标是其面向空间发展的核心问题。2014年MUDGE J 和TARBELL T 提出了一种傅里叶原位定标法［17］，他们通过偏振干涉理论获得了滤光器探测光强与LCVR 相位偏移之间的函数关系，通过傅里叶分析获得LCVR 的偏移量。尽管如此，该文章仅给出了1 级滤光器的理论推导，并且假设滤光器各级之间完全线性无关，其测量误差会随LCVR 相位偏移显著增大。因此，本文在该方法的基础上，给出了7 级滤光器理论公式，并考虑了各级之间的非线性关系，通过傅里叶分析和非线性拟合相结合实现可调谐液晶双折射滤光器的高精度原位定标。

本项研究降低了可调谐液晶双折射滤光器的空间应用风险，为我国科学家提出的太阳极轨探测、环日探测、L5 探测、太阳立体探测等卫星计划实现高灵敏度磁场、速度场测量奠定基础［18］。

1 可调谐液晶双折射滤光器

可调谐液晶双折射滤光器的基本原理如图1 所示。图1（a）为一个经典的7 级双折射滤光器，每一级均采用了图1（b）所示的宽视场和可调谐设计。由于每一级两端均有两个偏振片，因此，各级之间的偏振干涉相互独立。根据偏振光理论，光经过第i级后的透射率与波长的关系如式（1）所示，其中Δn为冰洲石晶体（calcite）的双折射率，di为第i级冰洲石晶体的厚度，δiLC为第i级LCVR 的相位延迟。值得注意的是，由于LCVR 的厚度约5 μm，远小于冰州石厚度；而且对于太阳磁场测量，滤光器的自由光谱范围一般在1.4 nm 以内；因此，此处假设LCVR 的相位延迟在自由光谱范围内不随波长变化。

图1 可调谐液晶双折射滤光器原理图Fig.1 Schematic diagram of tunable liquid crystal birefringent filter

为了实现窄带滤光，滤光器各级的冰州石厚度以2 倍指数递增，即d7=2d6=…=26d1，7 级滤光器的透过率与波长的关系如式（2）和图1（c）所示。此外，通过控制LCVRs 的相位延迟可实现滤光器的透过中心波长移动。最终实现了双折射滤光器的窄带滤光和调谐。

2 原位定标方法

理论上，光线经过可调谐液晶双折射滤光器后的总能量是守恒的。如果观测目标的光谱是均匀无吸收或无发射（即连续谱），则观测目标的光经过双折射滤光器后，探测光强不会随滤光器LCVR 相位延迟的改变而变化，因此无法实现双折射滤光器的原位定标。相比之下，太阳磁场的测量恰恰相反。由于太阳磁场测量中，双折射滤光器测量的是太阳光球层夫琅和费磁敏谱线，该谱线会在0.03 nm 带宽范围内有很强的吸收，此时，探测光强随滤光器LCVR 相位延迟的变化而出现周期性变化，这为实现原位定标提供了可能。

为了便于简化和推导，重新整理式（2）成如下形式，其中，σ0为中心波长的波数，ai和bi为冰洲石双折射光程的一次泰勒展开系数。

由于滤光器的自由光谱范围小于中心波长，则有σ1≪σ0；忽略σ1的二次项，且在中心波数σ0处有σ0ai=k，k∈N，此时，式（3）可进一步简化为

设太阳的归一化强度谱为Tsun(σ)，双折射滤光器的前置滤光片透过率为Tprefilter(σ)，则太阳光经过可调谐液晶双折射滤光器后探测器得到的总强度如式（6）所示，

式中，太阳光谱、前置滤光片透过轮廓以及冰洲石的双折射系数均为常数，因此，总探测强度仅仅是滤光器各级LCVR 的相位延迟δiLC的函数。

当LCVR 的相位延迟存在漂移时，δiLC可由描述，其中为LCVR 输出量（已知量），ΔδiLC为LCVR 存在的未知漂移误差。带入式（6）后得到

通过控制每级LCVR 的输出，可使得第i级的在［-180° 180°］范围内变化，而其他级的=0，j≠i。此时，式（7）变为

由式（8）可知，当仅仅调节第i级的LCVR 时，探测强度为的余弦函数，周期为2π；通过傅里叶分析或三角函数拟合可得到该余弦函数的相位偏移量，即

式（10）中，ψi是ΔδiLC(i=1，…，7)的非线性函数，依次调节每级的LCVR，通过傅里叶分析可得到7 个非线性方程，然后通过式（9）建立相位延迟漂移误差ΔδiLC(i=1，…，7)之间的理论模型，通过非线性拟合可求得所有LCVRs 的误差量，从而实现可调谐液晶双折射滤光器的原位定标。

该方法采用傅里叶分析降低了探测强度以及本底噪声的影响，采用非线性拟合兼顾了各级之间的相互串扰，提高了定标精度；而且一次测量即可完成定标，测量方法便捷，且无额外的硬件需求，极大的满足了可调谐液晶双折射滤光器的空间应用需求。

3 误差分析

3.1 仿真分析

由式（9）易知，基于傅里叶分析的非线性拟合原位定标方法的测量误差依赖于太阳辐射强度谱Tsun(σ)、前置滤光片透过轮廓Tprefilter(σ)、冰洲石的双折射光程参数（ai，bi，i=1，…，7）以及非线性拟合误差。为了分析该定标方法的各项误差，选用的可调谐液晶双折射滤光器参数如表1 所示，该参数是“子午二期工程”全日面矢量磁像仪中双折射滤光器的设计值。该滤光器的观测谱线为太阳夫琅和费磁敏线Fe I 532.418 nm，太阳辐射强度谱使用BASS2000 的太阳光谱数据，前置滤光片选用Andover 公司产品，太阳光谱和前置滤光片的透过轮廓如图2 所示。

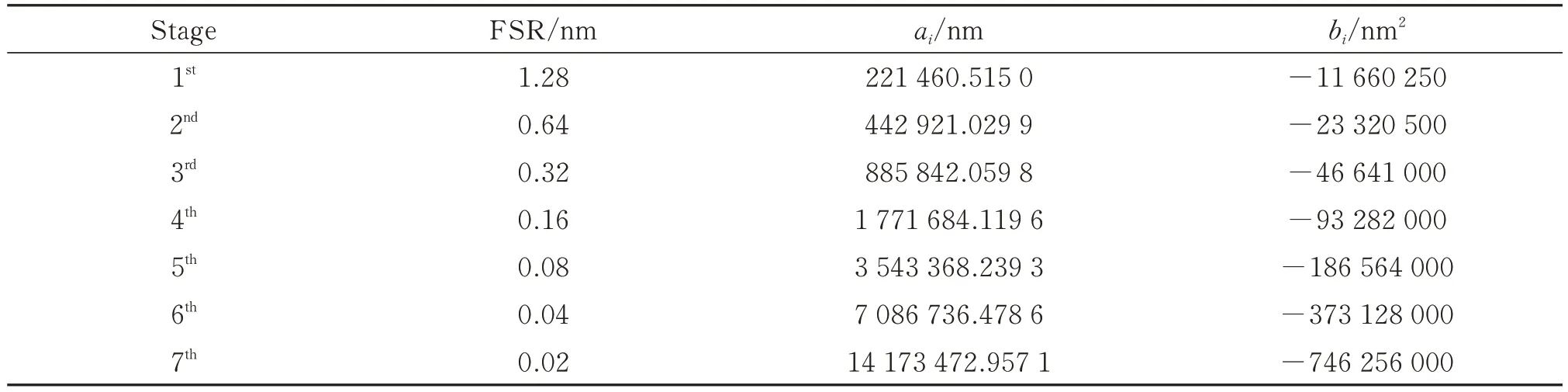
表1 可调谐液晶双折射滤光器设计参数Table 1 Design parameters of tunable liquid crystal birefringent filter

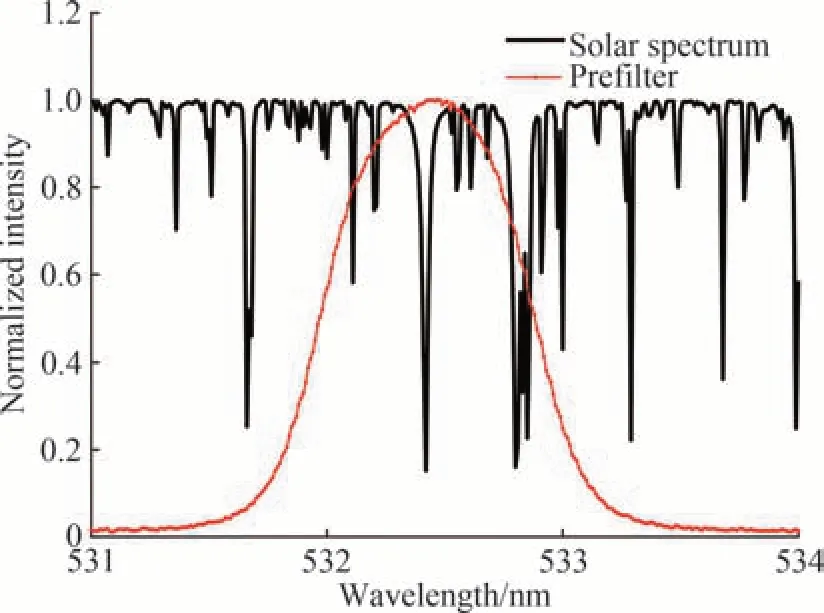
图2 太阳光谱和前置滤光片的归一化强度Fig.2 Normalized intensity of solar spectrum and prefilter

3.1.1 非线性拟合误差

非线性拟合的主要误差来自于初始值问题。为了定标方法的便捷和唯一性，所有定标假设初始值均为0。在这一基本前提下，图3 给出了LCVRs 相位延迟漂移在［−50° 60°］时定标方法的测量误差。其中图3（a）为傅里叶分析结果，对应MUDGE J 方法的测量误差；图3（b）为基于傅里叶分析的非线性拟合定标方法测量误差（下文统称为新方法）。可以发现，MUDGE J 等的傅里叶分析法误差明显偏大，说明各级之间的非线性相关对测量影响较大。新方法在考虑了非线性后，［−45° 58°］度范围内测量误差低于0.1°；当LCVRs 偏离更宽范围内时，由于非线性拟合中存在反三角函数以及局部极小值的不确定性，导致该方法的误差也迅速增大。结果表明，新方法在LCVRs 相位延迟偏离±45°范围内具有非常好的定标效果。

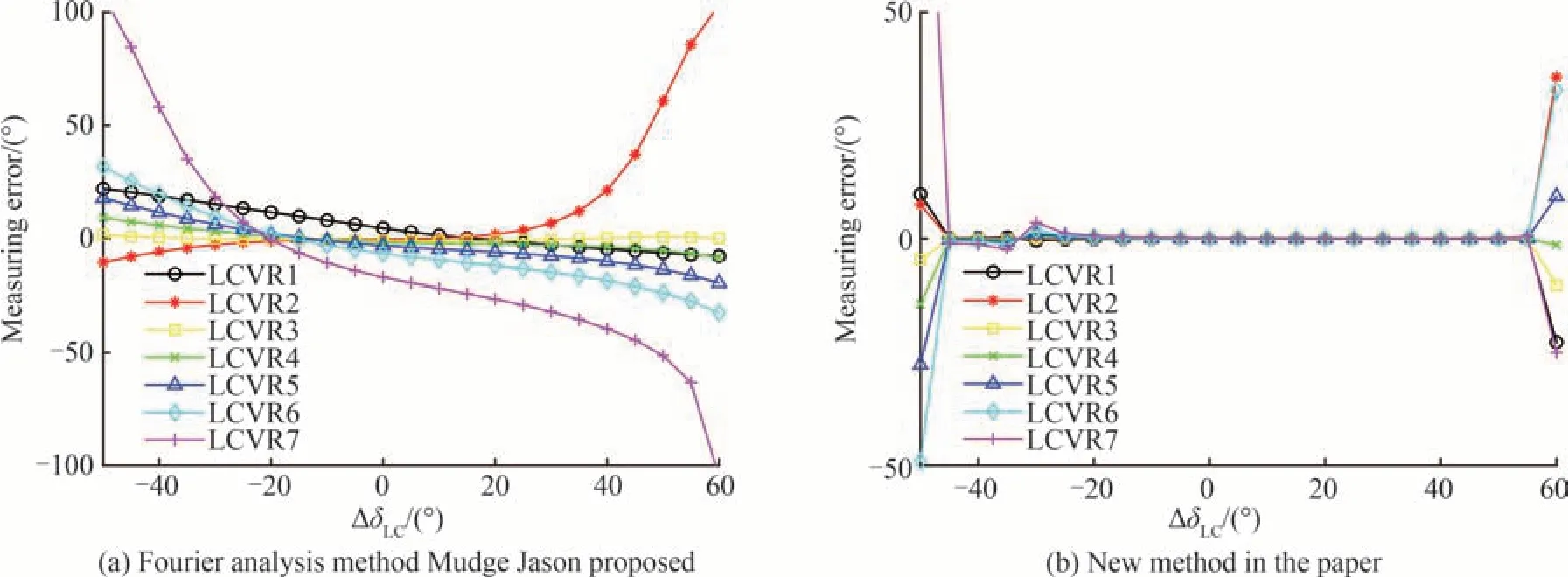
图3 两种定标方法的测量误差对比Fig.3 Comparison of measurement errors between two methods

3.1.2 前置滤光片中心波长漂移

由于加工误差，前置滤光片的中心波长不可避免的偏离实际观测波长。为了分析中心波长漂移对定标方法的影响，仿真分析中将图2 中的前置滤光片轮廓中心位置偏移±0.5 nm，同时假设各级LCVR 的相位延迟漂移为−45°，以分析LCVR 漂移量较大的情况下，滤光片中心波长漂移对定标误差的影响。测量结果如图4 所示，可以发现中心波长漂移量在［−0.17 μm 0.07 μm］范围内，LCVR 相位延迟测量误差在0.1 度以内；偏离该范围，定标误差开始显著变化。对比图2 可以发现，这是由于当中心波长漂移过大时，太阳光谱的其他吸收谱线占比增大，从而影响了定标精度。

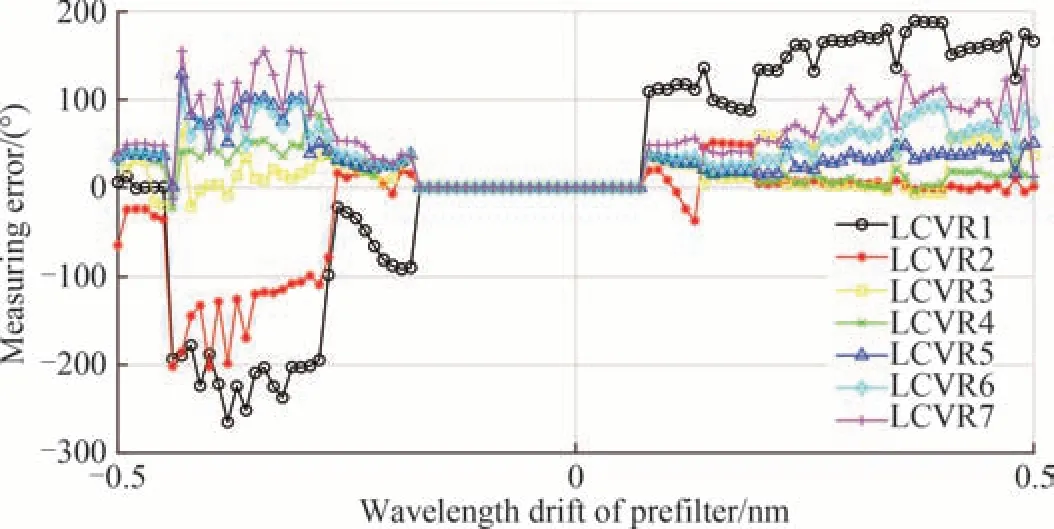
图4 前置滤光片的中心波长漂移对定标误差的影响Fig.4 The influence of the center wavelength drift of the prefilter on the measuring error

3.1.3 冰州石参数加工检测误差

对于冰洲石晶体而言，影响定标精度的因素主要有两个：冰洲石的厚度加工误差以及冰洲石双折射光程的一阶色散误差。同样假设各级LCVR 相位延迟漂移−45°，图5（a）给出了冰洲石厚度加工误差对LCVR相位延迟测量精度的影响，加工误差在±100 μm 范围内，相位延迟测量误差在5°以内；加工误差在±10 μm范围内时，相位延迟测量误差在1°以内。图5（b）给出了冰洲石的一阶色散相对误差与LCVR 相位测量精度的关系，可以发现一阶色散变化±50%，相位从延迟测量误差在5°以内；一阶色散变化±10%，相位延迟测量误差在2°以内。

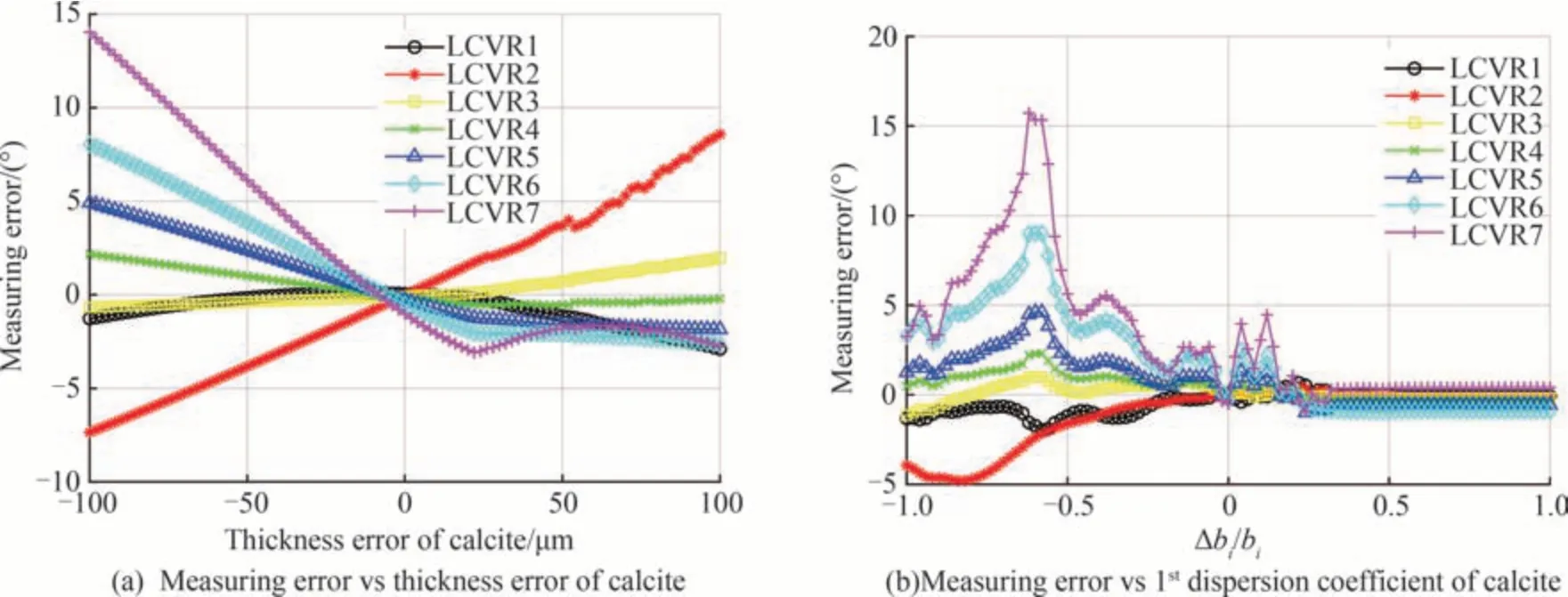
图5 冰洲石光程参数加工检测误差对定标精度的影响Fig.5 Influence of optical path error of calcite on measuring error

3.2 误差评估

仿真分析表明：各级LCVR 相位延迟漂移量在±45°，新定标方法相位延迟测量精度在0.1°以内；前置滤光片中心波长漂移量在［−0.17 nm 0.07 nm］范围内，相位延迟测量精度可达到0.1°；冰洲石加工误差在±10 μm 范围内时，相位延迟测量误差在1°以内；一阶色散变化±10%，相位延迟测量误差在2°以内。实际情况下，前置滤光器的中心波长漂移量一般可控制在±0.02 nm 范围内，并且可通过精密温控实现更高精度的控制；冰洲石厚度加工误差可控制在μm 量级；一阶色散系数测量误差在1%以内。因此，基于傅里叶分析的非线性拟合定标法可有效实现可调谐双折射滤光器的定标。

4 实验研究

为了验证该定标方法的有效性，利用“子午二期工程”全日面矢量磁像仪的可调谐液晶双折射滤光器在中科院国家天文台怀柔太阳观测基地进行了实验研究。实验测试装置如图6 所示，首先通过定天镜将太阳光引入实验室，然后太阳光依次经过280 mm 口径的反射式望远镜、准直镜及反射镜，将光束引入到可调谐液晶双折射滤光器。光线经过滤光器后依次通过成像镜、光栅组件后最终由探测器接收。实验装置中，光栅的使用便于实时的获取和分析双折射滤光器的透过轮廓变化。

图6 实验装置Fig.6 Experimental setup

实验测试过程如下：

1）通过双折射滤光器透过轮廓的实时显示，调整双折射滤光器的LCVRs，获得一个比较理想的透过轮廓，此时假设Δδi=0，i=1，…，7；

2）以15°步长在［−150° 150°］范围内依次调节各级的LCVRs，LCVR 每调一个位置，探测器测量一个透过轮廓，积分获得一个光强点，测量数据如图7（a）所示。然后通过傅里叶分析法和本文提出的定标法，计算得到一组实际Δδi，i=1，…，7，定义此时的LCVRs 的相位值为双折射滤光器最佳位置（即线心位置）；

图7 实测数据Fig.7 Measurement data

3）将双折射滤光器的LCVRs 的相位延迟量均偏移线心−20°。仍然以15°步长在［−150° 150°］范围内依次调节各级的LCVRs，LCVR 每调一个位置，探测器测量一个透过轮廓，积分获得一个光强点，测量数据如图7（b）所示。然后通过傅里叶分析法和新定标法，计算得到另一组实际Δδi，i=1，…，7，该相位值与−20°之差即为测量误差；

4）同理，将LCVRs 的相位延迟量依次偏移线心−40°、−60°得到图7（c）～7（d）；

5）利用MUDGE J 的傅里叶方法和本文提出的新方法可计算得到LCVRs 的相位延迟量依次偏移线心−20°、−40°、−60°时的测量误差，如图8（a）所示；

图8 测量结果Fig.8 Measuring result

6）利用（5）中得到的各个新的LCVR 线心值可获得一系列对应的滤光器透过轮廓，如图8（b）所示。

图8（a）的相位延迟测量误差表明，基于傅里叶分析的非线性拟合法（new method）在LCVR 偏离线心−40°以内测量误差在5°以内，对应双折射滤光器（带宽0.01 nm）的线心漂移量小于0.000 3 nm；相比而言，傅里叶分析法（old method）的测量误差相对较大，在20°以内。当相位延迟偏离−60°时，两种方法均失效，且滤光器次宽级和最窄级的延迟误差最大。图8（b）给出了通过两种定标方法定标后的滤光器透过轮廓，基于傅里叶分析的非线性拟合法在40°内透过轮廓无明显变化，而傅里叶分析法中，当相位偏移−40°时次宽级明显增大，同时谱线中心波长位置由于最窄级的误差增大而偏移。

5 结论

本文在MUDGE J 提出的傅里叶分析法基础上提出了基于傅里叶分析的非线性拟合法用于可调谐液晶双折射滤光器的原位定标。该方法兼顾了滤光器各级之间的相互串扰，提高了定标精度；而且一次测量即可完成定标，测量方法便捷，且无额外的硬件需求，满足了可调谐液晶双折射滤光器的空间应用需求。仿真分析表明，各级LCVR 相位延迟漂移量在±45°，该定标方法相位延迟测量精度在0.1°以内；前置滤光片中心波长漂移量在［−0.17 nm 0.07 nm］范围内，相位延迟测量精度可达到0.1°；冰洲石加工误差在±10 μm 范围内时，相位延迟测量误差在1°以内；一阶色散变化±10%，相位延迟测量误差在2°以内。最后通过实验研究，分析了两种方法的测量误差，结果表明LCVR 漂移量在−40°以内，基于傅里叶分析的非线性拟合法测量误差在5°以内，对应双折射滤光器（带宽0.01 nm）的线心漂移量小于0.000 3 nm；而傅里叶方法的测量误差在20°以内。当LCVR 偏移量达到−60°时，两种测量方法均失效。实验结果和仿真分析基本一致。