星光成像的大气影响研究(Ⅱ):大气湍流
2023-07-03陶志炜戴聪明武鹏飞任益充梅海平童杰骆传凯青春冯云松魏合理饶瑞中
陶志炜,戴聪明,武鹏飞,任益充,梅海平,童杰,5,骆传凯,青春,冯云松,魏合理,饶瑞中
(1 中国科学院合肥物质科学研究院 安徽光学精密机械研究所 中国科学院大气光学重点实验室, 合肥 230031)
(2 国防科学技术大学 电子对抗学院 红外与低温等离子体安徽省重点实验室, 合肥 230037)
(3 先进激光技术安徽省实验室, 合肥 230037)
(4 合肥工业大学 物理学院, 合肥 230601)
(5 中国科学技术大学研究生院科学岛分院, 合肥 230026)
0 引言
人类利用恒星来进行导航,最早可追溯到古代人们通过北极星来确定方位。直到20 世纪50年代,星敏感器的横空出世,大大提升了恒星导航的精度。星敏感器是一种高精度的姿态敏感测量仪器,它通过成像系统对星空成像,测量恒星矢量在星敏感器坐标系中的分量,利用已知的恒星精确位置来确定载体相对于惯性坐标系的三轴姿态[1]。星敏感器导航技术的高精度、抗干扰性强、可不依赖其它系统进行独立导航等优点在近地空间各类机载、舰载、车载平台上有着广泛的应用[2]。
早期,星敏感器应用于卫星平台,承担了卫星姿态测量的任务,是卫星平台不可或缺的测量设备。由于大气层外可近似看成是真空环境,因此,星载星敏感器在工作时几乎不受大气的影响,其测姿精度通常可达到角秒级甚至亚角秒量级。随着空天观测平台的发展以及大气层内星敏感器观测高度的降低,大气对恒星探测的影响愈发显著,星敏感器在成像时不可避免的会受到地球大气背景辐射、湍流、折射等因素的影响。白天大气分子与气溶胶粒子会对太阳光产生散射,使得天空产生复杂的背景光,对星敏感器在白天观星时产生极大的干扰,严重降低成像的信噪比,使得恒星目标湮没在背景中,无法识别[3]。另一方面,大气分子与气溶胶粒子的存在会使得星光传输产生衰减,再加上大气本身存在折射率起伏,还会影响光波的相位,并对振幅产生调制,引发星光的闪烁和抖动[4-10]。由于大气折射率随高度存在一定变化,因此当星光经过大气传输时,大气折射会延长星光的传输路径,改变星光的传输方向,严重影响星光导航的精度。
为了定量评估大气对星光成像的影响,本系列文章之一着重研究了星光成像中恒星“看的见”这一重要问题。其次,为了进一步获取恒星的位置采用星敏感器进行定位和导航,还需着重研究恒星“看的准”这一问题,即如何评估星光成像的大气湍流和大气折射影响。实际上,关于星光大气湍流影响的研究最早可追溯至对星光图像结构和运动的研究。这种运动在几何光学角度看来最直接的影响就是使得星光产生一定程度的角向位移[4]。随着光波随机介质传输理论的建立[11],研究人员才逐步弄清星光抖动产生的原因,即由于大气湍流使得波前产生倾斜导致的。除此之外,大气湍流会使星光产生另一个高阶效应,即对星光的强度产生调制[12](折射率的随机起伏会对星光的能量产生耗散和起伏),进而使得星光发生“忽亮忽暗”的现象,这便是人们常说的闪烁效应[4-10]。
本文是星光成像大气影响三部分研究(背景辐射、湍流及折射)的第二部分,目标在于构建星光大气湍流传输的数理模型,并针对我国幅员辽阔特点,选取典型地区,获取测试数据,优化完善我国典型区域星光闪烁和抖动的数据模型。首先,结合大气湍流廓线数据,获得典型地区星光传输链路的相位屏分布特性和湍流特性。其次,结合分步式光传输方法,研究星光经过大气湍流传输后的闪烁量、到达角以及到达角起伏等物理量的变化规律,定量评估大气湍流对星光成像的影响。本文的结果对于指导星敏感器的设计、星像质心算法的开发研究具有一定的指导价值。
1 星光大气湍流传输模型
1.1 分步式光传输模型
星光成像大气湍流仿真的核心问题在于研究大气湍流对星光传输的影响。为了从数值角度给上述问题一个定量的结果,首先介绍星光大气湍流传输的分步式光传输模型,其主要思想是将大气信道看成一系列的湍流相位屏的组合,每个相位屏会在光束上引入一个满足大气湍流特性的随机相位ϕ,并将两个相位屏之间的传输过程看成真空环境下的Fresnel 衍射[13-14]。值得说明的是,每个相位屏不会导致光束振幅发生改变,而是通过真空衍射不断改变光束强度的分布情况,如图1 所示。对于每一段的传输过程,可描述为[14]
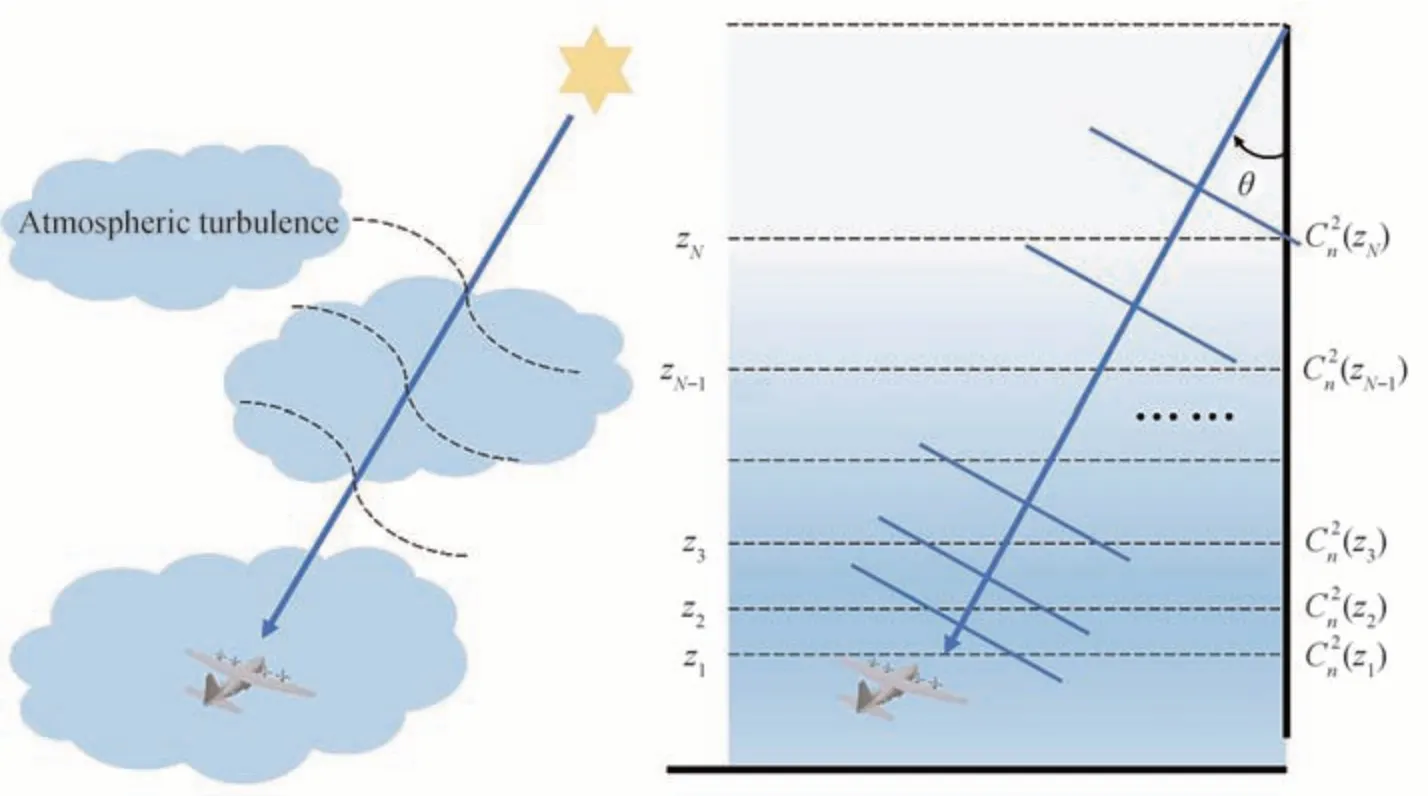
图1 星光大气湍流传输的原理图和星光传输的分步式大气传输模型Fig.1 Schematic diagram of the split-step beam propagation model
1.1.1 相位屏生成
针对第一个问题,目前常用的构造相位屏的方法是基于傅里叶变换得到的,其基本原理是利用湍流折射率谱和复高斯随机数矩阵产生相空间复随机场,然后进行逆傅里叶变换获得二维相位的空间分布,其过程可表示为[13,15-17]
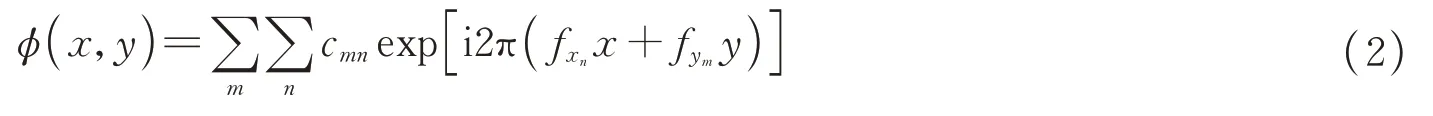
需要说明的是,虽然采用傅里叶变换产生湍流相位屏的方法较为简单,但使用该方法生成的相位屏明显具有低频不足的缺点,这是因为采用该方法生成的相位屏的最小频率为Δfx,其中不包含和这部分频率的贡献。为了补偿相位屏中低频成分的贡献,国内外相关学者提出了一种次谐波补偿的相位屏生成方法,其数学形式为[13,18]
式中,p为次谐波级数,且次谐波频率间隔为Δfp=1/(3p L)。本文采用次谐波补偿的傅里叶变换法来改善相位屏模拟大尺度的统计特征。
1.1.2 湍流描述
针对本文研究内容,首先需得到我国典型地区不同时段的湍流廓线,其次根据湍流廓线设置相应的相位屏分布。众所周知,大气湍流的分布具有一定的垂直结构,其通道内的光学湍流强度变化可描述为折射率结构常数C2n随高度h的函数。常见的C2n垂直廓线的参数化模式有HV 模式[19],HMN 模式[20]以及Dewan 模式[21]等。然而,由于光学湍流的变化往往具有一定的地域和季节等特征,因此若盲目采用上述模式计算星光大气湍流传输后的结果,会得到不符合我国局部的实际地理和大气状况的结果。因此,本文的计算和分析并未采用经典的参数化模式,而是基于ERA5 数据1ERA5 是欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)第五代全球大气再分析数据集,提供的变量达到240 个,包含不同的大气参量,如温度、相对湿度、风速等,使用户能精确地分析过去长时间范围大气的状态。数据下载地址详见:ERA5-Land hourly data from 1950 to present (copernicus.eu)。并结合光学湍流预报方法[22-23],在得到的湍流廓线数据基础上进行的。为了计算典型区域不同时刻的星光闪烁情况,本文选取了2008年1月1日三沙(地理位置:112.5°E, 17°N,温度:21.6 ℃,湿度:73.2%,压强:1 017.69 hPa)、大柴旦(地理位置:95.25°E, 37.75°N,温度:−12.6 ℃,湿度:41.8%,压强:665.79 hPa)以及合肥(地理位置:117.25°E, 31.75°N,温度:0.81 ℃,湿度:50.9%,压强:1 030.27 hPa)三地一天四个时间段的湍流情况进行计算,相应的湍流廓线如图2 所示。
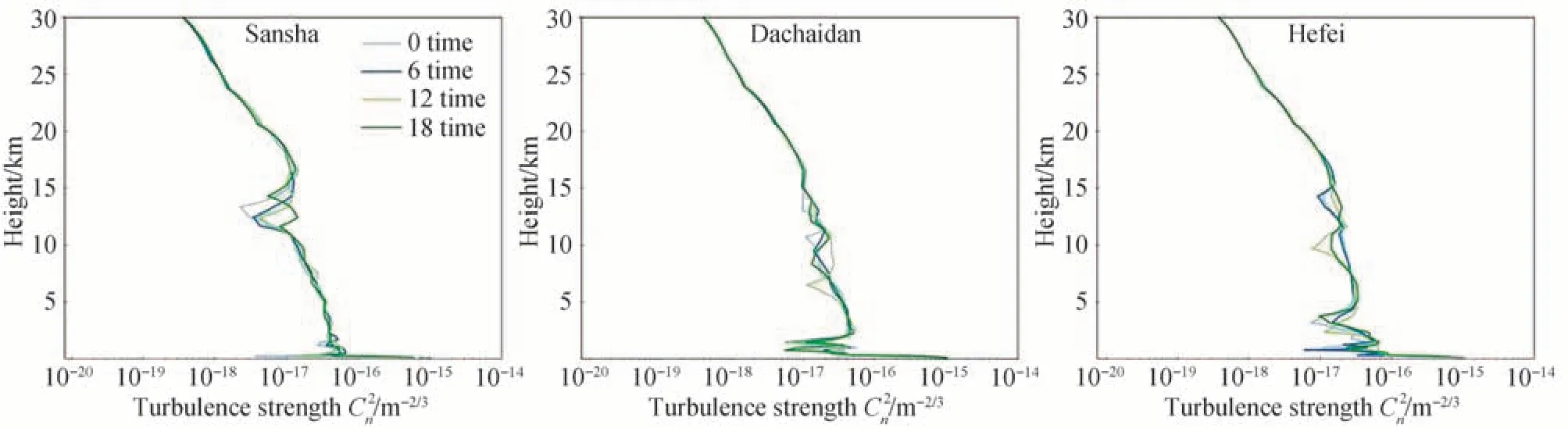
图2 2008年1月1日三沙、大柴旦、合肥三地一天四个时间段的湍流廓线图Fig.2 Turbulence profiles at Sansha, Dachaidan and Hefei for four time periods of one day on January 1, 2008
1.1.3 相位屏分布
根据以上得到的典型区域不同时刻的湍流垂直分布情况,便可设置星光大气传输信道相应的相位屏分布。一般而言,对于折射率起伏均匀的光传播路径,一般设置等间隔的相位屏;而对于非均匀路径下的光传播,如地球大气中的上行或下行传播问题,由于传播路径上的折射率起伏强度不相等,若仍设置等间隔的相位屏,则会导致强起伏区不能被充分采样,而弱起伏区被过度采样。这不仅使得数值模拟不能真实地反映光传播的实际过程,又增大了不必要的计算量。因此本文采用等Rytov 指数间隔相位屏分布方式来进行数值仿真[24]。具体原理可分为以下几个步骤(详见附件流程图)。
1)设定常数c,使得相邻两层相位屏的Rytov 指数σ2R(Δzi)≡c。
2)根据近地面的C2n(0)以及,计算第一层相位屏对应的高度,用于设定初始值。
3)对于第i个相位屏到i+1 个相位屏的间距Δzi,采用第i层相位屏对应高度的C2n(zi)和恒等式进行计算。
4)迭代第3)步,直到相位屏间距总和等于总的传输距离,停止迭代。
上述采用等Rytov 指数间隔的相位屏分布是假定天顶角为零的条件下进行,若天顶角为θZ且上述生成的相位屏的高度分别为h1,h2,…,hn,则应调整相位屏分布的高度为h1secθZ,h2secθZ,…,hnsecθZ。
对于天顶角为θZ的各层相位相位屏的大气相干长度r0i,采用式(4)进行计算。
1.2 星光闪烁
上一节介绍了星光大气湍流传输的分布式光传输模型,结合典型地区湍流廓线设置相应的相位屏分布,便可得到星光大气湍流传输后的结果。根据已知星光大气湍流传输后的电场,结合式(5),可计算星光的闪烁指数,它通常刻画了接收端星光的强度起伏情况[25]
式中,符号I和分别表示光场强度和系综平均值。一般而言,在任意起伏条件下,闪烁指数一般不能获得一个明确的解析表达式,但对于Kolmogorov 谱情况下的平面波而言,任意湍流强度下垂直信道的闪烁指数可表述为[26-27]
式中,σ2R为Rytov 指数有
式中,h为观测高度,θz表示天顶角的大小。需要说明的是,式(6)给出的结果是平面波垂直信道的点闪烁公式,而式(5)给出的计算公式具有一定的普适性,可计算任意孔径区域内的闪烁指数。一般而言,采用数值接收电场计算闪烁指数时总是会得到一定区域范围内闪烁指数平均的效果(这是由于网格的空间分辨率决定的)。众所周知,闪烁指数一般与接收端望远镜接收孔径大小成反比,因为较大的望远镜将平均孔径上的波动。孔径平均闪烁应小于用点接收器测量的闪烁。因此,为了将数值结果与理论结果进行对比,需对数据结果除以一个孔径平均因子,才可与理论结果进行对比。对于平面波而言,孔径平均因子可表示为
式中,D代表望远镜的接收口径大小,有限面积上的任意起伏条件下闪烁方差σ2I(D)为[28]
1.3 远场成像
根据接收电场不仅可以计算星光经过大气湍流后的闪烁值,还可计算星光经望远镜远场成像后的光斑的抖动量、到达角以及到达角起伏,后者通常是星光到达像面上传播方向的度量。一般而言,星光经过大气湍流传输后被接收端望远镜接收,而后在远场成像,其成像模型可等效为物体紧贴棱镜的成像方式[13]。因此,星光的远场光斑可表述为二维远场衍射积分[13]
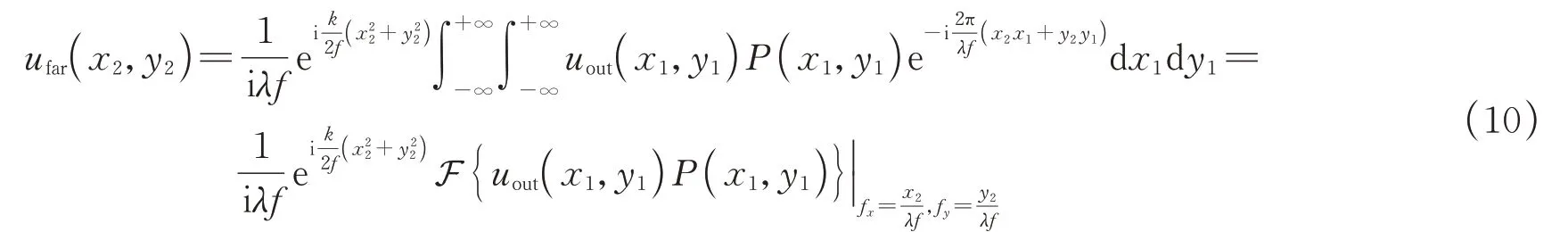
式中,uout(x1,y1)为星光经大气湍流传输后的电场,P(x1,y1)为望远镜的光瞳函数,f代表望远镜的焦距。根据式(10),可计算远场光斑的抖动量。值得注意的是,由式(10)还可以看出,如若需要统计远场光斑的抖动量,则需要事先知道成像系统的焦距f。换句话说,远场光斑的抖动量与成像系统的焦距有关,但这一点是我们不希望的。因此,为了研究大气湍流本身对于远场光斑抖动的影响,本文采用到达角来描述星光的抖动,其可表述为

式中,Δr代表远场光斑的抖动量。例如:若接收端望远镜的焦距为1 m 且到达角为2 μrad,则远场光斑相应的抖动量为2 μm。另一方面,根据式(11)还可计算远场光斑的到达角起伏,这一点也是本文所关注的。
2 星光大气湍流影响分析
2.1 闪烁指数的变化
图3 给出了不同观测高度下(观测高度为0 km、1.5 km、3 km、4.5 km、6 km、7.5 km)三沙、大柴旦、合肥一天四个时间段的星光闪烁随天顶角的变化情况,其中不同形状的曲线代表不同观测高度下的闪烁结果,每幅图中的插图代表数值仿真结果与根据式(6)理论计算结果的对比情况。
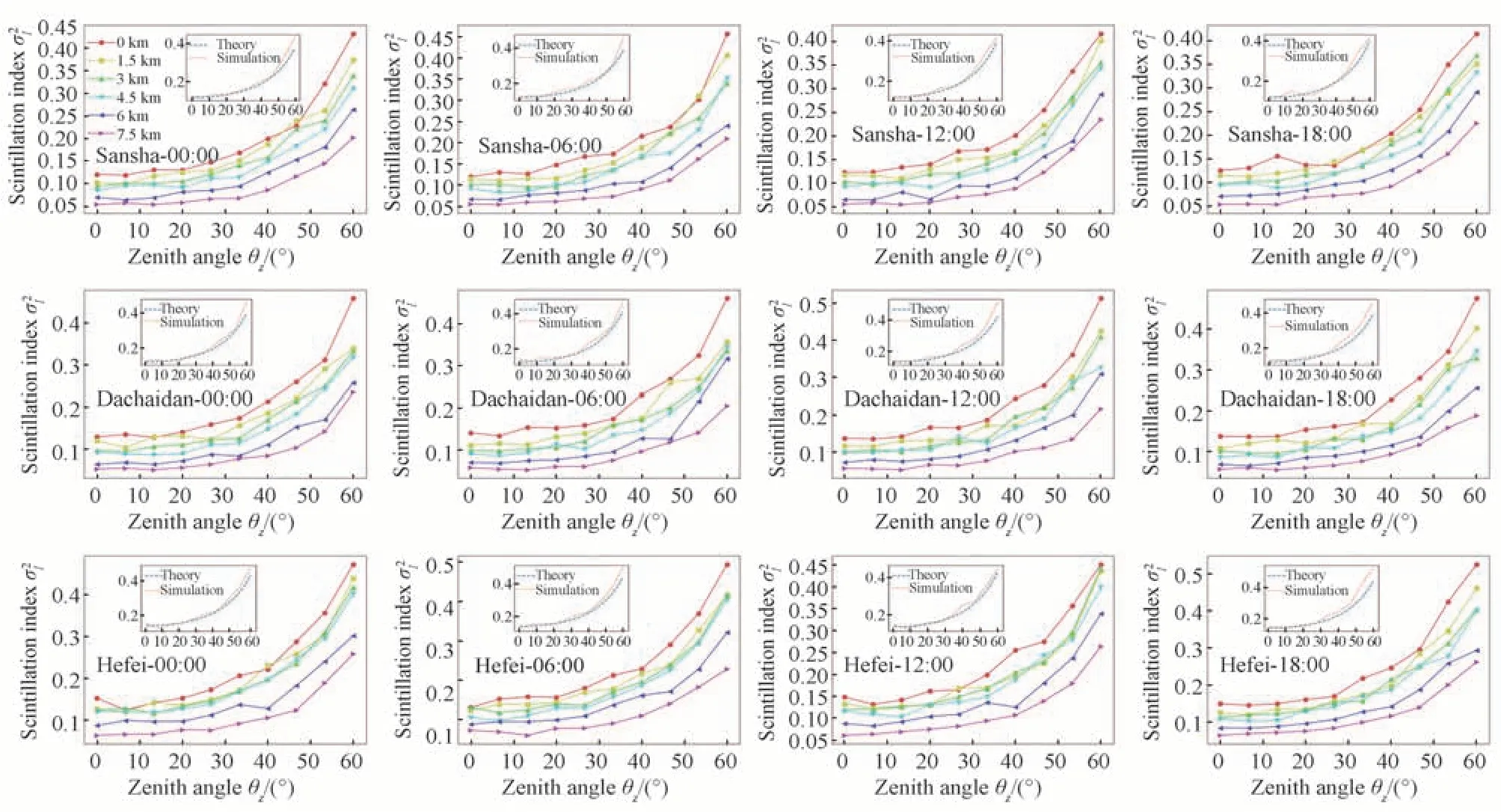
图3 不同观测高度下三沙、大柴旦、合肥三地一天四个时间段星光闪烁指数随天顶角的变化情况Fig.3 Scintillation index of starlight as a function of zenith angle in Sansha, Dachaidan and Hefei under different observation altitudes
从图3 中插图可以看出典型区域不同时间段数值仿真计算得到的星光闪烁指数基本与式(6)给出的理论结果相吻合,说明采用上述数值仿真方法计算星光抖动相关指标具有一定的可行性。除此之外,可以看到,当天顶角逐渐增加时,数值仿真与理论值误差相对较大,这是因为随着天顶角增大,传输距离逐渐变化,如果采用与天顶角较小时一样的网格尺寸,便会产生一定的计算误差。
对比图3 中不同子图结果可以发现:不同区域、不同时间段以及不同观测高度下,星光闪烁指数均随着天顶角的增加不断增加,这是因为随着天顶角的增加,传输距离逐渐变大,此时星光大气传输会受到更多的湍流影响。除此之外,对比不同观测高度下的星光闪烁指数,可以看到不同区域不同时间段指定天顶角情况下,星光闪烁指数随着观测高度的增加不断较小,这是因为近地面湍流较强,湍流强度随高度呈减小趋势(详见图2 中的大气湍流廓线)。对比同一地区不同时间段的星光闪烁随天顶角的变化,可以看出不同时间段星光闪烁指数之间的差异较小,且对于不同地区而言,星光闪烁最大值出现的时刻也并不相同(例如:对于三沙地区而言,0 点和6 点的闪烁指数要略高于12 点和18 点;对于大柴旦地区而言,正午时刻星光的闪烁指数略高于其他时间段)。最后,对比不同地区的闪烁指数,可以发现不同区域的星光闪烁值之间的差异较小,但相比于沿海三沙地区,内陆地区(大柴旦、合肥)星光闪烁指数要略大于三沙地区。
2.2 到达角和到达角起伏的变化
图4 和图5 给出了观测高度为0 km、1.5 km、3 km、4.5 km、6 km、7.5 km 情况下三沙、大柴旦、合肥一天四个时间段的星光远场光斑到达角及到达角起伏随天顶角的变化情况,其中不同形状的曲线代表不同观测高度下的结果。
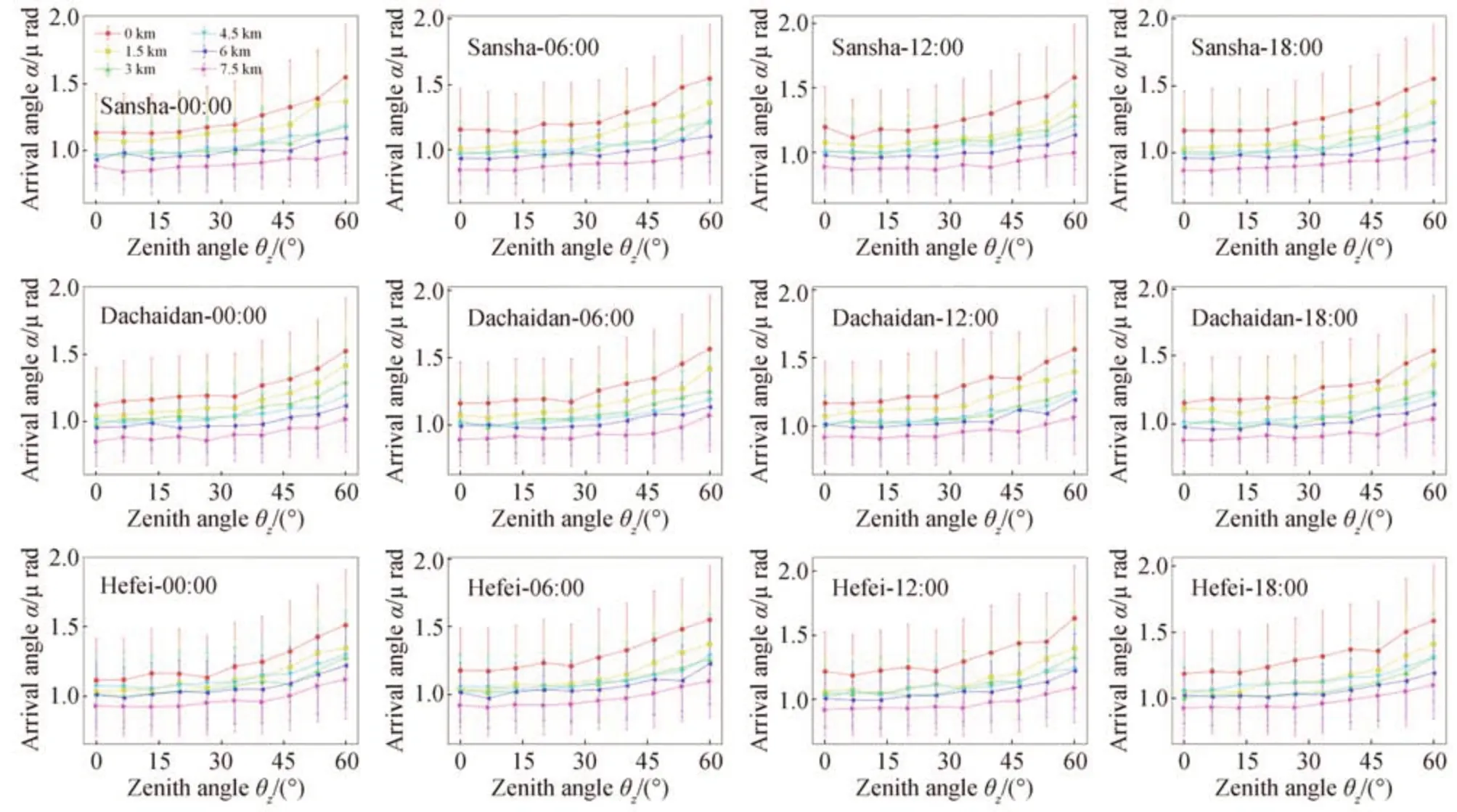
图4 不同观测高度下三沙、大柴旦、合肥三地一天四个时间段远场光斑的到达角随天顶角的变化情况Fig.4 Arrival angle of the far-field optical spot as a function of the zenith angle at four times of the day in Sansha, Dachaidan and Hefei under different observation altitudes
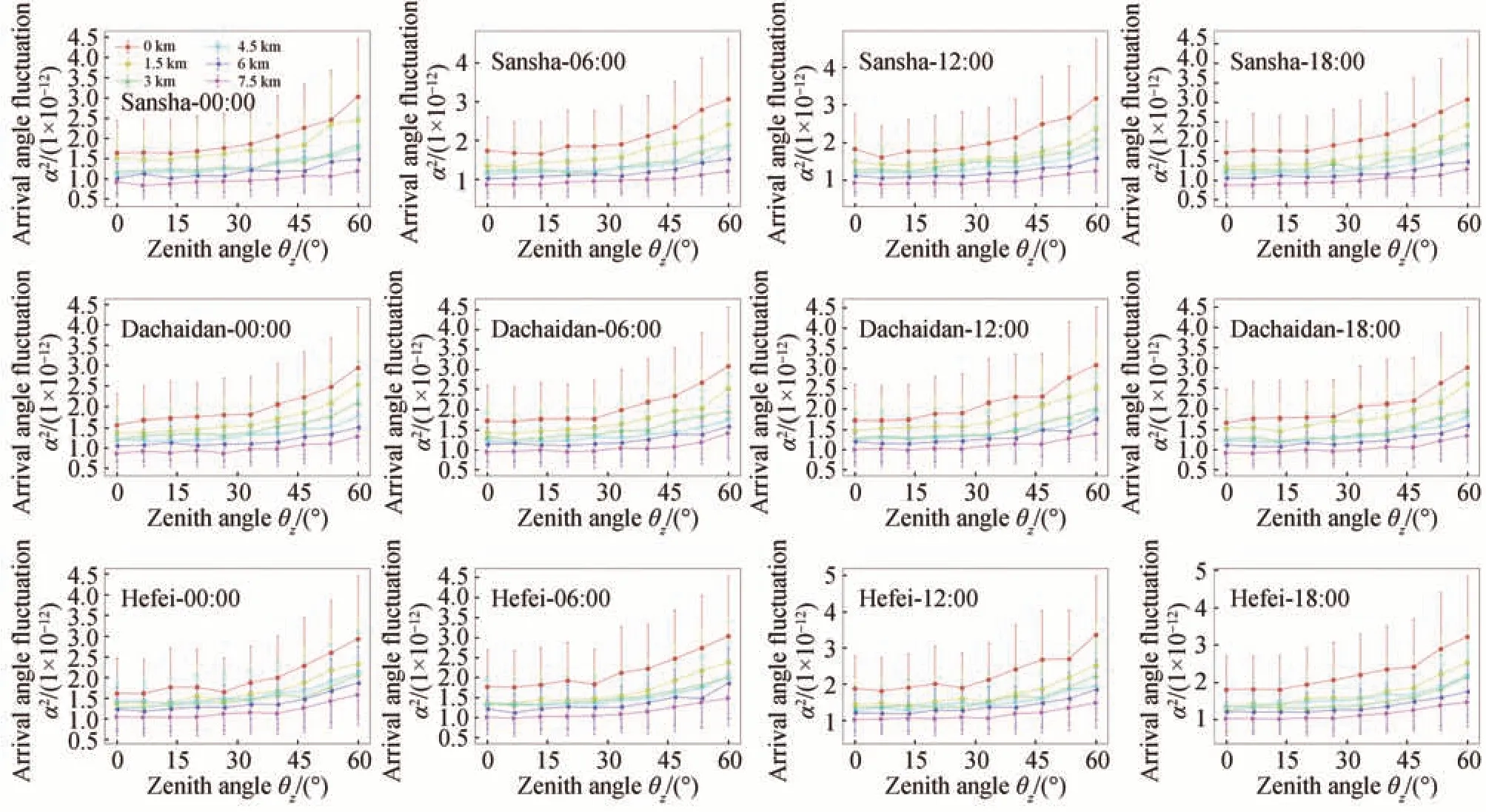
图5 不同观测高度下三沙、大柴旦、合肥三地一天四个时间段远场光斑的到达角起伏随天顶角的变化情况Fig.5 Arrival angle fluctuation of the far-field optical spot as a function of the zenith angle at four times of the day in Sansha,Dachaidan and Hefei under different observation altitudes
由图4、5 中可看出典型区域,不同时刻以及不同观测高度的到达角、到达角起伏随天顶角的变化整体呈现相同的趋势,到达角和到达角起伏整体与星光闪烁指数呈正相关关系,到达角主要在μrad 量级变化,到达角起伏主要在10−12量级上变化。从对比图中的到达角以及到达角起伏的变化曲线,可以发现:典型区域,不同时刻以及不同观测高度下的到达角、到达角起伏整体随天顶角的增大而逐渐增大。随着观测高度的增加,这种增加逐渐减弱,特别是当观测高度大于3 km 时,到达角、到达角起伏几乎不随天顶角的增加而变大,这是因为随着观测高度的增加,高空湍流相对较弱,这时改变观测仰角,星光大气传输并不会受到更多的湍流影响。另一方面,对于特定天顶角情况下,不同区域四个时间段的到达角和到达角起伏随着观测高度的增加逐渐减小。这种减小趋势在观测高度在0~3 km 变化时表现最为明显,这是因为随着观测高度的增大,该高度层的湍流急剧减小的原因导致的。
3 结论
本文构建了星光大气湍流传输模型,着重研究了大气湍流对星光成像的影响。基于ERA5 数据和光学湍流预报方法得到大气湍流参数廓线,采用等Rytov 指数间隔方法给出了典型地区不同时刻的星光传输链路的相位屏分布情况,结合分步式光传输模型,计算了典型地区不同时刻及观测条件下星光的闪烁指数,通过对比星光闪烁的理论值,验证了数值计算的可靠性。与此同时,本文研究了湍流大气中星光远场光斑质心的抖动特性,得到了典型观测高度及观测天顶角情况下的恒星到达角及到达角起伏。研究发现:星光抖动的到达角和到达角起伏整体呈现相同的变化趋势,并且与星光的闪烁指数呈正相关关系。当观测高度小于3 km 时,随着星敏感器的观测高度增加及其观测天顶角的减小,星光抖动逐渐减小,当观测高度大于3 km 时,由于此时大气湍流强度较弱,星光抖动几乎不受观测高度、天顶角的变化而变化。综上所述,提高星敏感器的观测高度和观测仰角能一定程度上减轻星光成像的大气湍流影响。
附录
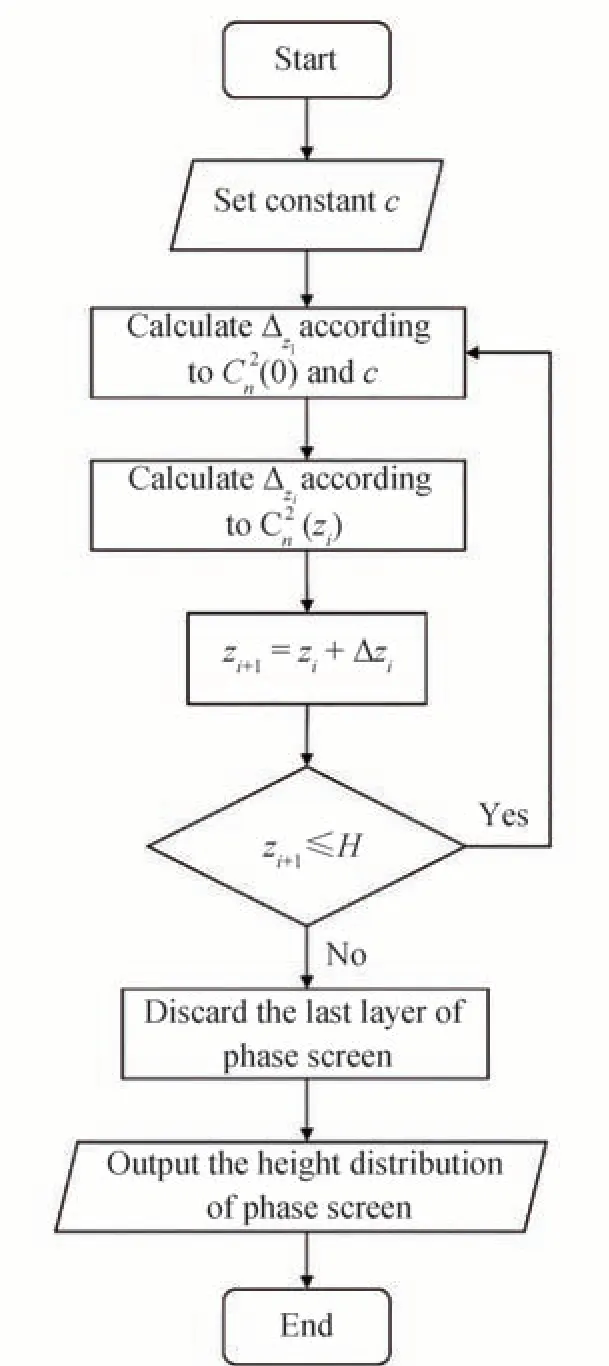
图A1 等Rytov 间隔的相位屏高度分布的流程Fig.A1 Flow chart of the phase screen height distribution with equal Rytov intervals
