基于格子Boltzmann 方法的动压气体轴承黏性热耗散研究*
2023-07-02鹿翔宇陈振乾
鹿翔宇 许 波 陈振乾
(东南大学能源与环境学院 江苏南京 210096)
动压气体轴承因其转速高、 寿命长、 低摩擦、 无污染等优点, 被广泛应用于透平膨胀机、 涡轮压气机、 飞机发动机、 制冷机等高速旋转涡轮机械中, 在航空航天、 能源与动力等领域发挥着十分重要的作用[1]。 在动压气体轴承的运转过程中, 虽然转子和箔片不会直接接触, 但是轴承间隙内流体的高速剪切流动依然会产生大量的热量, 容易引起温度的分布不均和局部过热, 进而烧蚀箔片。 此外, 轴承的零部件也会因温度的升高而导致刚度和阻尼发生变化, 产生热变形, 对轴承的性能造成一定的影响[2]。 因此, 研究动压气体轴承的气动热和热特性规律, 以及相关的冷却方法具有重要意义。
国内外学者对于轴承热特性的研究主要集中在近20 年。 SALEHI 等[3-4]使用基于Couette 近似的简化能量方程和可压缩雷诺方程获得了箔片气体轴承中的气膜温度, 并采用有限差分法和迭代法对简化表达式进行求解。 PENG 和KHONSARI[5-6]考虑空气的可压缩性和黏温特性以及轴承表面的柔度, 建立了用于预测箔片气体轴承三维温度场的热流体力学模型, 并研究了冷却流量的影响, 发现膜的温升随转速的增加呈指数增长。 LEE 等[7-8]提出了一个包含箔片结构和转子的轴承传热模型, 计算了润滑气膜、 顶箔、 波箔、 轴承套和转子的温度, 并采用广义雷诺方程和三维能量方程预测了气膜温度。 SIM 和KIM[9]通过轴的二维轴对称热传导、 气膜中的三维能量传输、 箔片热阻和轴承壳体中的三维热传导模型, 建立了箔片气体轴承的热流体动力学模型, 该模型还结合了箔片接触热阻和入口流混合的分析模型, 以提高模型精度。 SAMANTA和KHONSARI[10]分析了箔片气体轴承的热弹性不稳定问题, 推导出一个封闭的解析解来预测在波箔中发生热弹性不稳定的临界速度, 并验证了波数和膜厚对失稳临界速度的显著影响。 ZDZIEBKO 和MARTOWICZ[11]开发了箔片气体轴承的有限元模型, 分析表明, 波箔与顶箔和轴承套接触次数最多的区域, 也就是顶箔的热量传递到轴承衬套和其他轴承的部件最集中的区域。
以上对于箔片气体轴承热特性的研究, 主要采用的是雷诺方程结合能量守恒方程的宏观方法。 然而轴承间隙的尺寸一般非常小, 通常在几十微米的级别[12], 间隙内的流场已经处于滑移区, 甚至过渡区,会出现一些微观效应, 例如速度滑移、 温度跃变、 黏性热耗散等, 此时采用一些微观方法将更加合适。 分子动力学(Molecular Dynamics, MD) 模拟和直接模拟蒙特卡罗(Direct Simulation Monte-Carlo, DSMC)方法等基于粒子的方法在微流场模拟方面取得了一定的进展[13-14]。 然而, 对于大多数实际应用来说, 它们的计算量过于庞大。 介观的格子玻尔兹曼方法(Lattice Boltzmann Method, LBM)[15]自从被提出以来, 已经被广泛应用于微尺度流动的研究, 其计算量与宏观方法相当, 比较适合用于文中的研究。 与经典雷诺润滑方程相比, LBM 可以捕捉更加微观的现象,边界条件实施简单。 并且当轴承间隙内气流处于过渡区时, 此时不满足连续性假设, 宏观雷诺方程不再适用, LBM 将成为十分有潜力的研究方法。 然而鲜有学者将LBM 用于动压气体轴承的黏性热耗散研究。
目前, 格子Boltzmann 方法应用在热流动研究的主要有3 种模型: 多速度 (Multi-speed, MS) 模型[16-17], 双分布函数(Double-Distribution Function,DDF) 模型[18-23]和混合模型[24]。 MS 模型是等温LB模型的直接延伸, 其利用密度分布函数的高阶速度矩来描述能量方程。 DDF 模型利用了2 种不同的分布函数, 一种用于流场, 另一种用于温度场。 在混合方法中, 流动模拟采用LB 法, 而温度场的求解则采用传统的数值方法, 如有限差分法。 1998 年, HE 等[18]基于DDF 模型引入内能分布函数, 第一次提出了包含黏性热耗散和压缩功的热格子Boltzmann 模型, 随后有学者在其基础上进行了一定的改进[20,25]。 2007年, GUO 等[21]在单一速度分布函数的基础上定义了代表总能量的分布函数, 基于DDF 模型提出了总能形式的含有黏性热耗散和压缩功的热LBE 模型。 该方法在演化过程中不涉及复杂的导数项, 计算简单,数值稳定性高, 文中将基于该模型研究动压气体轴承的热特性。
LBM 虽然在研究热流动方面已经发展了20 多年, 但是目前相关研究依然是针对一些比较简单的物理模型, 像轴承间隙这种弯曲变截面的高速剪切微通道鲜有研究。 因此本文作者将LB 方法应用到该领域, 基于GUO 等[21]提出的总能形式的DDF 离散速度模型, 得到了可以应用在贴体网格中的有限差分格式的显式LB 方法, 并引入Langmuir 滑移边界, 实现对轴承间隙微通道的模拟, 并研究了不同温差大小、 偏心率、 转速以及温度阶跃对于黏性热耗散分布规律的影响, 从更加微观的层面探究了轴承间隙黏性热耗散的机制。
1 数值模型
1.1 有限差分DDF-LBE 模型
文中使用的包含黏性热耗散和压缩功的总能形式双分布函数离散速度模型[21], 其基于Hermit 多项式展开, 并保留至二阶项。 它由密度分布函数和总能分布函数构成, 其中总能包括内能和机械能, 2 个分布函数的演化方程为
式中:fi和hi分别是i方向的密度分布函数和总能分布函数;和是对应的平衡态分布函数;ci是粒子的离散速度;τhf=1/τh-1/τf, 其中τf和τh分别为动能和内能松弛时间;Zi=ci·u-u2/2,u是宏观速度;Fi和qi是与外力有关的2 个项。
对于二维九速(D2Q9) 模型, 2 个平衡态分布函数为
式中:R为气体常数;T0为参考温度;ρ为宏观密度,p0=ρRT0; 权重系数w0=4/9,w1=w2=w3=w4=1/9,w5=w6=w7=w8=1/36, 离散速度ci取值为
2 个外力项Fi和qi的表达式为
式中:a为质量力, 总能,cv为定容比热容。
为稳定可靠地求解离散方程(1)、 (2), 对其进行有限差分格式的离散, 在时间[tn,tn+1] 内进行求积, 并对演化方程中的碰撞项做如下处理:
式中:tn+1=tn+Δt; 碰撞算子,,Si=-τfZiΩf/τhf+qi。
为了能够显式求解上式, 可以引入2 个新的分布函数,
式中:ωf=Δt/τf,ωh=Δt/τh。
将新的分布函数代入式(8)、 (9), 就能得到可应用于贴体网格中的有限差分形式的玻尔兹曼方程:
动能和内能的松弛时间有如下关系:
式中:μ为动力黏度;p是压力;κ为热传导系数;cp是定压比热容。
于是普朗特数为Pr=μcp/κ=τf/τh。
为了能够将上述方程应用到曲线坐标系ξ中, 以方程(12) 为例, 对其空间梯度项进行如下离散[26]:
∂fi/∂ξβ的离散理论上可以采用中心差分格式或者二阶迎风插值格式进行求解:
式中: Δξβ是ξβ方向的网格间距。
中心差分格式数值耗散少, 但不稳定, 而迎风插值格式虽相对稳定, 但是却有较强的数值耗散。 为了解决这些问题, 可以将上述2 种方法组成一种混合的差分格式:
其中, 0≤ϑ≤1 是调节中心差分格式和迎风插值格式权重的系数。 根据文献的建议, 在后续研究中无特殊说明时取0.1。
为了让LB 方法可以模拟微尺度流动现象, 需要处理2 个重要问题, 第一个就是解决松弛时间τf和流动Kn数(Kn=λ/L,λ为分子平均自由程,L为特征长度) 之间的关系, 通过结合动力学理论和LBM的运动黏度表达式, 可得[27]:
式中:H为通道的高度。
由于轴承间隙内的流场压力和温度分布不均, 因此对上式进行如下修正:
式中:ρ0为参考密度;T0为参考温度。
1.2 边界条件
将LB 方法应用到热微流动的另一个重要问题就是如何处理速度滑移和温度阶跃边界条件。 文中采用了Langmuir 滑移模型[28], 它反映了气体分子和壁面之间的界面相互作用, 可以表示为
式中: 下标w 代表壁面处的局部值; 下标g 代表靠近壁面处的局部值;αv和αT是与气体种类和壁面材料属性有关的调节系数。
为了方便确定这2 个调节系数, 可以将Langmuir滑移模型与Maxwell 滑移模型进行联立
式中:σv为动量调节系数;σT为热调节系数;σv和σT在文中没特殊说明的情况下均取1;γ是比热容比。
于是
式中:N=1/δx表示网格数量。
将Langmuir 模型的处理方法应用到非平衡外推边界中, 最终可以得到适用于当前模型的速度滑移和温度阶跃的边界格式:
式中:xw是边界处的节点;xg是与边界相邻的节点。
1.3 求解步骤
数值计算程序的大致流程如图1 所示。
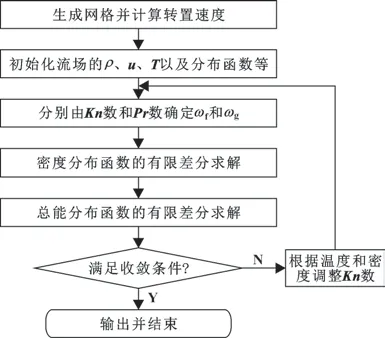
图1 计算流程Fig.1 Numerical calculation procedure
具体的实现步骤如下:
(1) 通过求解椭圆偏微分方程组生成贴体网格,并计算转置速度。
(2) 根据物理问题, 初始化网格节点的密度、速度和温度, 得到初始状态的密度分布函数和总能分布函数及其平衡态。
(3) 根据Kn数确定τf, 进一步得到ωf, 同理根据Pr数确定τh, 进一步得到ωh。
(4) 密度分布函数的求解: 根据式(14) 计算密度和速度, 由结合式(10) 可得fni, 随后根据式(19) 计算fni的有限差分, 最后根据式(12) 计算得到。
(5) 总能分布函数的求解: 根据式(14) 计算温度, 由结合式 (11) 可得hni, 随后根据式(19)计算hni的有限差分, 最后根据式(13) 计算得到。
(6) 判断速度和温度是否满足收敛条件, 如果不满足则根据温度和密度调整Kn数, 并重复步骤(3) — (6), 如果满足则输出结果并停止计算。
2 物理模型
简化后的动压气体轴承的示意图如图2 所示。 轴颈和轴承套的半径分别为r1和r2(r2=r1+C0, 其中C0为平均间隙), 最大间隙为hmax, 最小间隙为hmin。轴颈以速度ω顺时针旋转,e为偏心距, 则偏心率为ε=e/C0, 轴承的Kn数定义为Kn=λ/hmin。 轴颈表面的温度为T1, 轴承内表面的温度为T2, 两壁面的温差ΔT(=T1-T2) 可以采用无量纲数Eckert 数来表征,其定义为

图2 动压气体径向轴承简化示意Fig.2 Schematic of gas-lubricated journal bearing
式中:U为轴颈表面的线速度。
轴承的具体参数和运行工况范围见表1。

表1 轴承参数和运行工况Table 1 Bearing parameters and operating conditions
3 模型与可靠性验证
以圆柱热Couette 流为例, 对文中模型进行了验证。 其几何参数和贴体网格划分如图3 所示。 内外圆柱半径比Rβ=r1/r2=3/5, 内圆柱以线速度U顺时针旋转, 温度为T1, 外圆柱静止, 温度为T2。 考虑黏性热耗散, 圆周方向和半径方向的网格数分别为NX=188,NY=20。 圆柱热Couette 流的量纲一温度T*的解析解表达式[29]为
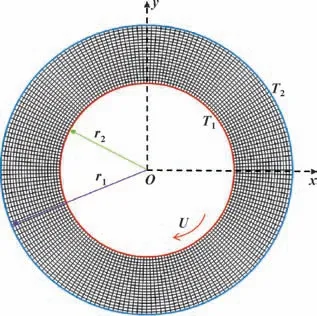
图3 圆柱热Couette 流示意Fig.3 Schematic of thermal cylindrical Couette flow
式中:r*=r/r1, 为量纲一半径。
文中在Pr=0.7 的情况下, 分别模拟得到了Ec数为1、 5、 10 的3 种径向温度分布, 结果见图4。 可以发现, 在相同网格分辨率下, 数值模拟结果与理论解吻合良好, 最大相对误差不超过0.8%, 证明模型精度较高。
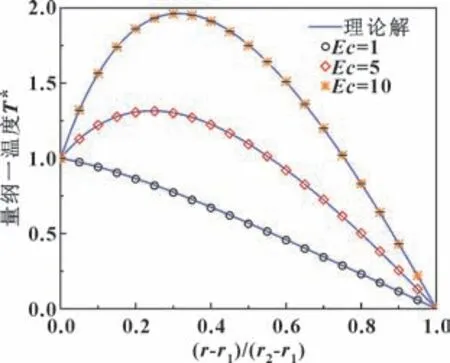
图4 不同Ec 数下的温度分布Fig.4 Temperature distribution at different Ec number
在后续的模拟中, 为了排除网格数量对于轴承间隙黏性热耗散计算结果的影响, 还需进行网格独立性验证。 文中对轴承半径为8 mm, 间隙尺寸为25 μm,偏心率为0, 转速为5×104r/min 的动压气体轴承间隙热流动进行模拟,Ec数固定为10。 间隙流域圆周方向和半径方向的网格数分别为10 053×5、 20 106×10、 30 159×15、 40 212×20、 50 265×25。 5 种网格分辨率下模拟得到的间隙流场中最高的量纲一气膜温度如图5 所示。 可以看出, 随着网格数量的增加, 黏性热耗散产生的最高温度也随之升高, 但是升高的速率逐渐减小, 说明增加网格数对于提升模型精度的作用逐渐降低。 综合考虑模型精度和计算资源的消耗, 文中最终选取的网格分辨率为30 159×15。
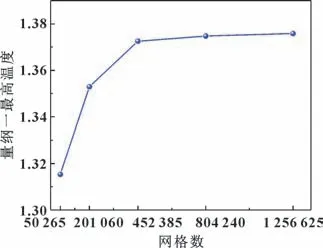
图5 网格独立性验证Fig.5 Grid independence verification
4 结果与讨论
4.1 不同Ec 数的影响
轴承在运转过程中, 由于散热条件的不同, 一般轴颈表面和轴承套内表面的温度是存在差异的。 为了更好地探究黏性热耗散的变化规律, 假设轴颈和轴承套两侧为定温壁面, 且存在一定的温差, 并用Ec数来表示温差大小。 轴承转速为5×104r/min, 偏心率保持0.6, 图6 所示为不考虑两壁面处温度阶跃时,不同Ec数下间隙内最高气膜温度处径向量纲一温度T*(=(T-T2)/(T1-T2)) 的分布。 可以看出, 在Ec数较小时, 两侧温差较大, 间隙温度分布几乎呈线性分布, 此时是以热传导为主, 黏性耗散的影响基本可以忽略。 而当Ec数较大时, 黏性热耗散的作用明显, 温度呈抛物线分布, 流场中最高温度出现在靠近轴颈侧, 且流场中大部分的温度都已经高于T1。 总体来看, 随着Ec数的增加, 也就是温差的减小, 黏性耗散作用增强, 气膜温度的最大值是逐渐递增的。

图6 不考虑温度阶跃时不同Ec 数下最高气膜温度处径向量纲一温度分布Fig.6 Radial dimensionless temperature distribution at the highest gas film temperature for different Ec number without considering temperature jump
图7 所示为考虑了温度阶跃情况下的不同Ec数时的温度分布。 当Ec=1 时, 轴颈侧的温度小于T1,温度阶跃为正值; 而当Ec=2 时, 轴颈侧的温度大于T1, 此时温度阶跃变成了负值。 随着Ec数的增加,两侧的温度阶跃均呈增大的趋势, 说明温度阶跃的影响将变得更加显著。 因此, 轴颈和轴承套两侧温差的增大, 将更有利于削弱黏性热耗散的影响。
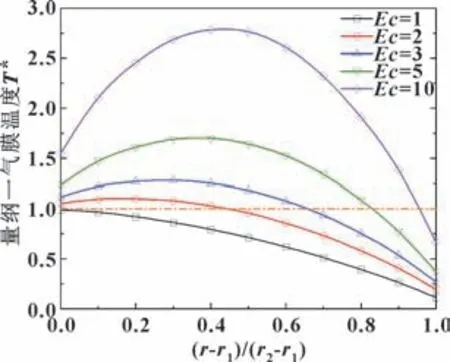
图7 考虑温度阶跃时不同Ec 数下最高气膜温度处径向量纲一温度分布Fig.7 Radial dimensionless temperature distribution at the highest gas film temperature for different Ec number considering temperature jump
4.2 不同偏心率的影响
图8 所示为转速5×104r/min, 轴承平均间隙为25 μm,Ec数为10, 不考虑温度阶跃时不同偏心率下间隙内最高气膜温度处径向量纲一温度分布。 可以看出, 随着偏心率的增加, 间隙中的气膜最高温度也逐渐升高。 这是因为, 当偏心率变大时, 轴承间隙尺寸在圆周方向的变化幅度增加, 意味着气膜的挤压作用增强, 黏性热耗散的量也随之增大。 此外, 出现最大气膜温度处的位置随着偏心率的增加逐渐由靠近轴颈侧向流场中间偏移, 表明间隙内的流动逐渐接近于平板Couette 流。

图8 不考虑温度阶跃时不同偏心率下最高气膜温度处径向量纲一温度分布Fig.8 Radial dimensionless temperature distribution at the highest gas film temperature for different eccentricity ratios without considering temperature jump
图9 展示了考虑温度阶跃时不同偏心率下最高气膜温度处径向量纲一温度分布。 随着偏心率的增加,轴颈和轴承套两侧的温度阶跃均增大, 并且轴颈侧的温度阶跃量要小于轴承套侧的温度阶跃量, 原因是轴颈侧的温度梯度要小于轴承套侧的温度梯度。 由于温度阶跃的发生, 当偏心率为0.8 时, 轴承套侧的温度已十分接近轴颈侧的温度, 流场中的温度基本都在T1之上, 因此在大偏心率情况下, 温度阶跃的影响不容忽略。
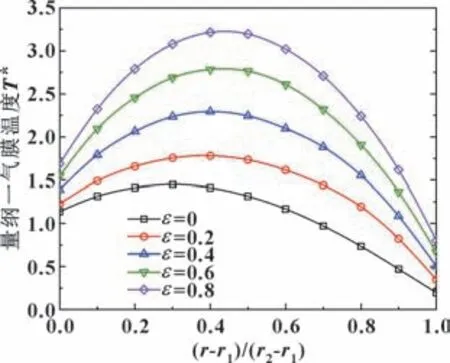
图9 考虑温度阶跃时不同偏心率下最高气膜温度处径向量纲一温度分布Fig.9 Radial dimensionless temperature distribution at the highest gas film temperature for different eccentricity ratios considering temperature jump
为了更好地看出温度阶跃对于黏性热耗散的影响, 图10 给出了不同偏心率下气膜温度最大值的变化。 可以发现, 最高气膜温度的值随着偏心率的增加而线性递增, 并且考虑温度阶跃时, 温度增加的速率更大, 再次印证了大偏心率情况下, 温度阶跃效应的影响显著。

图10 不同偏心率下的最高气膜温度变化Fig.10 Variation of maximum gas film temperature at different eccentricity ratios
4.3 不同转速的影响
图11 所示为偏心率ε=0.6, 轴承平均间隙为25 μm,Ec数为10, 不考虑温度阶跃时不同转速下间隙内最高气膜温度处径向量纲一温度分布。 可以看出,当转速从3×104r/min 增加到1.1×105r/min 时, 间隙内气膜温度的最高值增加明显。 这是因为, 随着轴承转速的提升, 间隙内流体的速度梯度增加, 流体剪切力增大, 黏性热耗散的作用增强。 此外, 虽然间隙的几何尺寸未发生变化, 但是随着转速的变化, 间隙内出现最大气膜温度的位置也在随之改变, 可能是因为离心力的变化导致的流体流动和传热特性的改变。

图11 不考虑温度阶跃时不同转速下最高气膜温度处径向量纲一温度分布Fig.11 Radial dimensionless temperature distribution at the highest gas film temperature at different rotational speeds without considering temperature jump
图12 所示为考虑温度阶跃时不同转速下最高气膜温度处径向量纲一温度分布。 可以看出, 随着转速的增加, 轴颈和轴承套两侧的温度阶跃均明显增大。 当转速为7×104r/min 时, 轴承套侧的温度已十分接近T1, 而当转速为9×104和1.1×105r/min 时,轴承套侧的温度将大于轴颈侧的温度T1, 此时间隙内整个流场的温度都高于T1, 这是由于温度阶跃和黏性热耗散共同作用的结果。
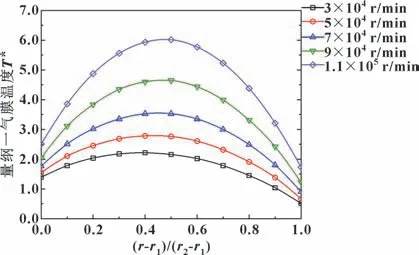
图12 考虑温度阶跃时不同转速下最高气膜温度处径向量纲一温度分布Fig.12 Radial dimensionless temperature distribution at the highest gas film temperature at different rotational speeds considering temperature jump
图13 给出了不同转速下间隙气膜最高温度的变化趋势。 气膜温度最大值随着转速的增加而增加, 并且升高的速率逐渐增大。 当考虑温度阶跃时, 最高气膜温度的增加速度和不考虑温度阶跃时比较接近, 说明不考虑温度阶跃对于不同转速下黏性热耗散计算带来的低估影响大致一样。
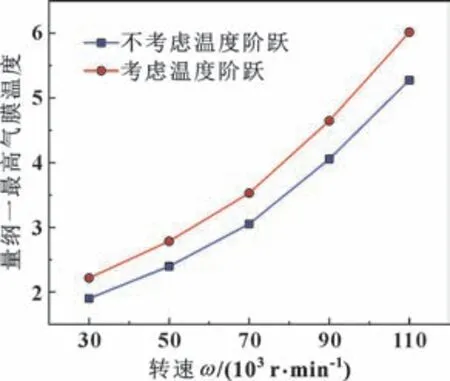
图13 不同转速下的最高气膜温度变化Fig.13 Variation of maximum gas film temperature at different rotational speeds
5 结论
(1) 轴颈和轴承套两侧温差较大时, 间隙温度几乎呈线性分布, 以热传导为主; 当轴颈和轴承套两侧温度较小时, 间隙温度呈抛物线分布, 此时黏性热耗散作用明显。
(2) 随着偏心率的增加, 最大气膜温度线性递增, 轴颈和轴承套两侧的温度阶跃也随之增加, 且偏心率越大, 温度阶跃对于黏性热耗散量计算的影响越大。
(3) 随着转子转速的增加, 最大气膜温度升高,变化的速率逐渐增大, 轴颈和轴承套两侧的温度阶跃增大, 但温度阶跃对于不同转速下黏性热耗散量计算的影响程度相差不大。
