指尖密封流动与变形三维双向耦合分析*

2023-07-02崔雪超胡娅萍李朋飞吉洪湖

润滑与密封 2023年6期

崔雪超胡娅萍李朋飞李华吉洪湖

（南京航空航天大学能源与动力学院江苏南京 210016）

指尖密封是20 世纪90 年代提出的一种新型柔性密封技术，可应用于航空发动机等旋转机械的气路密封及轴承腔润滑油密封。国外试验表明：相同条件下，指尖密封泄漏量仅为篦齿密封的10%～20%；与刷式密封相比，当泄漏量处于相近水平时，指尖密封的制造成本仅为刷式密封的40%～50%，同时能够避免刷束的断丝在油封中造成的严重磨损问题［1-2］。可见，指尖密封具备良好的应用前景，因此得到了国内外的广泛关注和研究。

指尖密封作为一种柔性密封结构，密封片组在上下游压差以及转子的作用下会发生轴向、径向与周向变形，该变形又会导致泄漏通道以及泄漏流动的变化，因此指尖密封的工作过程存在典型的流动与变形耦合的问题。泄漏特性是指尖密封最重要的性能之一，国内外对其开展了一系列实验研究。 MARIE［3］和BRAUN 等［4］针对指尖密封进行了动、静态实验，结果表明上下游压差越大密封泄漏量越大。白花蕾等［5-6］通过实验研究了指尖密封从初始使用到稳定后的泄漏流动，发现其初始使用时泄漏量较大，滞后明显；随着使用时间增加泄漏系数趋于稳定，稳定后指片之间的间隙对泄漏影响较大。胡廷勋等［7］对静态及不同转速下指尖密封的泄漏流动进行实验研究，结果表明泄漏量随着压差的增大而增大，随着转速的增大而减小。

针对指尖密封泄漏流动或固体变形的数值研究，主要分为三类。第一类是针对动压型指尖密封的浮升力垫片及其与转子之间间隙建立实体模型，采用流固耦合的方法对该间隙内泄漏流场与浮升力垫片的变形进行分析，如文献［8-14］的研究。第二类是将动压型指尖密封的浮升力垫片及其与转子之间间隙的流场等效为质量-弹簧动力学分析模型，构建该模型的等效力学参数和密封结构、工况参数的关系，在此基础上求解等效动力学模型的响应，继而计算出指尖密封的泄漏量，如文献［15-17］的研究。以上两类研究主要针对动压型指尖密封的浮升力垫片与转子之间间隙的泄漏流场开展，没有考虑实际工作中经由密封片之间间隙的泄漏、密封片的变形及其对泄漏的影响，也很难模拟密封片组与转子间处于接触甚至过盈配合时的工作性能。第三类是将密封片组处理为多孔介质，利用多孔介质模型对泄漏流动进行数值分析，如文献［18-21］的研究，这类研究考虑了经由密封片之间间隙的泄漏，也可计算密封片组与转子处于过盈配合时的泄漏量，但多为二维模型，而且多孔介质模型参数受密封片变形的影响，与密封结构及工况条件等均相关，通常需要采用试验数据进行标定。若采用未经标定多孔介质模型模拟则泄漏计算误差较大。

由此，本文作者针对密封片组结构的流动与变形提出一套基于多孔介质模型的三维双向耦合计算方法，应用多孔介质模型计算密封片组内的泄漏流场，密封片组的有限元变形计算考虑密封片间、密封片与后挡板间以及密封片与转子间的摩擦力。根据变形计算结果更新多孔介质模型的参数，重新计算泄漏流动直到收敛。文中采用该三维双向耦合计算方法对不同压差下指尖密封片的泄漏流动与固体变形进行数值模拟，分析压差对泄漏流动与变形的影响。

1 指尖密封泄漏与流动双向耦合分析模型

1.1 物理模型

如图1 所示，指尖密封由前挡板、隔片、若干密封片与后挡板组成。密封片是在一个薄片圆环上按照特定规律切割出许多小缝隙，形成一个个根部连在一起的细长条，这些宛若“手指” 的细长条称为指片。如图2 所示，指片自由端称为指尖靴，指尖靴以外的部分称为指梁。指片间的缝隙被相邻交错布置的密封片上的指片遮挡以阻挡泄漏，指尖靴通常与转子形成过盈配合以起到密封的作用。

图1 指尖密封结构Fig.1 Finger seal structure

图2 指尖密封片结构Fig.2 Finger seal laminate structure

1.2 密封片组泄漏流动的多孔介质模型

刷式密封刷束内的泄漏流动通常采用多孔介质模型进行模拟［22-23］，密封片组与刷式密封刷束的结构类似，其内部的泄漏流动也具有多孔介质渗透流的特点。基于此，文献［5］与文献［19］将密封片组结构处理为多孔介质求解其泄漏流场。文中也采用与文献［5］相同的多孔介质流动控制方程组，其动量方程中由于密封片组对泄漏流体的阻碍产生的附加源项为

式中：右端第一项为黏性损失项， 1／α为多孔介质的黏性损失系数；第二项为惯性损失项，C2为多孔介质的惯性损失系数。

白花蕾［5］将式（1）与刷式密封动量损失源项公式［22］进行类比并结合实验数据标定，求解得到适用于指尖密封的损失系数表达式为

式中：ε为多孔介质密封片组的孔隙率；S为其单位体积湿润面积；m和n为模型参数，通常根据试验数据标定。

考虑到文中的密封片结构与文献［5］的类似，对于多孔介质密封片组的模型参数m和n，取与文献［5］中相同的值作为初值，即分别为0.1 与0.17。因指梁和指尖靴的结构不同［19］，故文中分别针对指梁和指尖靴区域计算孔隙率和单位体积润湿面积，其计算公式均与文献［5］相同。

当指尖密封处于上下游压差为0、转子不旋转的非工作状态且密封片组与转子为过盈装配时，为文中密封的初始结构，由此求解多孔介质模型参数的初始值；当指尖密封处于有压差且转子旋转的工作状态时，密封片会发生变形，则多孔介质密封片组的孔隙率与单位体积润湿面积等参数也会产生变化。文中的数值计算，正是通过这两个模型参数的变化将指尖密封的泄漏流动和变形进行耦合。

2 双向流固耦合的计算方法

2.1 计算流程

根据指尖密封泄漏流动与固体变形的相互作用关系，文中采用三维双向耦合计算方法［24-25］；又由于密封片组的泄漏流场应用多孔介质模型求解，并非基于实体几何，故流场和变形计算采用分区迭代的弱耦合法，即在每一迭代步内分别求解泄漏流动控制方程与固体变形控制方程，然后两者通过流固耦合面传递数据，从而实现流动与变形的耦合。

密封的流动与变形三维双向耦合计算流程如图3所示。首先采用ANSYS 软件求解指尖密封在非工作状态下由于过盈装配产生的初始变形，根据变形后的几何结构计算密封片组多孔介质模型参数的初始值，并由ICEM 创建泄漏流场计算域及划分网格。根据多孔介质模型参数值，采用FLUENT 计算泄漏流场，获得泄漏量、速度与压力等数据。从FLUENT 输出压力分布数据并加载到ANSYS 固体有限元计算模型上，实现流场压力分布向密封结构的传递，然后进行密封片组的变形分析，包括其在流体压力作用下变形以及转子的离心膨胀，完成第一次迭代循环。导出变形后的密封结构，读取该结构的几何参数，代入孔隙率与单位体积湿润面积公式，计算更新多孔介质密封片组的模型参数。因转子离心膨胀值相对于泄漏流场模型尺寸十分微小，故忽略其对泄漏流场计算模型的影响。再次采用FLUENT 软件计算泄漏流场，实现流动与变形的双向耦合，之后，重新计算密封片组变形，完成第二次迭代循环。将第二次迭代计算所得的泄漏量与最大变形量与第一次迭代的结果进行对比，若满足收敛条件，则计算结束；否则继续进行迭代循环，直至收敛。

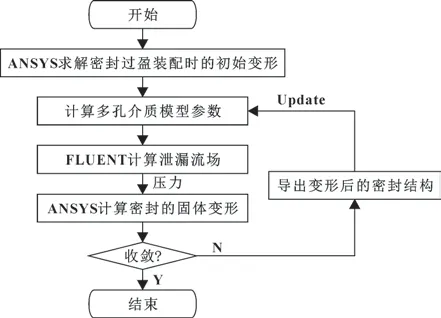
图3 流动与变形双向耦合迭代Fig.3 Iterative calculation of flow and displacement two-way coupling

上述密封流动与变形双向耦合迭代计算的收敛条件为

式中：和分别表示本次和上一次迭代计算所得的泄漏量；Di和Di-1分别表示本次和上一次迭代计算所得的最大变形量。

2.2 计算域及边界条件

根据指尖密封结构在周向上的周期重复性，为减少计算量，文中选取其沿周向10°的扇形段作为密封固体有限元变形计算模型，如图4 （a）所示，因前挡板仅对密封片起固定作用，不影响变形，故忽略。其中密封片的材料为65Mn，转子的材料为2Cr13，后挡板的材料为40Cr。密封固体变形计算边界条件的设置如图4 （b）所示：在流固耦合面F1 与F2 上施加流场传递的压力载荷；密封片与后挡板外环面6施加固定约束，密封片与密封片、密封片与后挡板及密封片与转子间设为摩擦接触，无润滑时，钢与钢形成的摩擦副摩擦因数为0.15［26］；转子转速恒为10 000 r／min，转子内表面及两个垂直于轴向的表面8 设置为无摩擦支撑边界，转子外表面为自由边界；挡板、中间密封片及转子的剖面7 设为周期循环边界。从高压上游到低压下游共三片密封片，分别命名为P1、 P2 及P3，其中高压和低压侧密封片均取完整的指片，中间密封片则取一片完整指片和两片的半指片，如图5 所示。

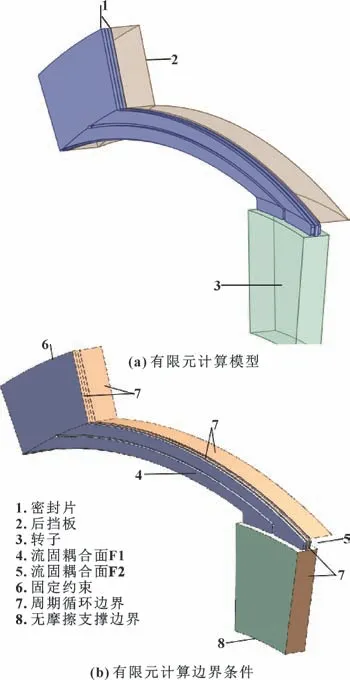
图4 有限元计算模型及边界条件Fig.4 Finite element computational model （a） and boundary conditions （b）

图5 密封片的排布Fig.5 Detail of the seal laminates

泄漏流场计算模型如图6 所示，沿轴向分为上游流体域、多孔介质密封片组区域、下游流体域。图4和图6 中所示的F1 与F2 分别为密封片组与上游流体域及下游流体域交界的流固耦合面，迭代计算时在流固耦合面上进行数据传递。泄漏流场计算模型边界条件的设置如图6 所示，进口面设为压力进口边界，文中算例分别设为0.1、 0.3、 0.5 MPa，出口面设为压力出口边界，文中恒设为0，转子表面设为无滑移旋转壁面，前后表面为周期边界，其他表面均设为无滑移静止壁面。

图6 泄漏计算模型及边界条件Fig.6 Leakage computational model and boundary conditions

2.3 网格划分及独立性验证

泄漏流场计算模型采用ICEM 软件划分网格，全域为六面体网格，其中多孔介质密封片组区域及近壁区进行网格局部加密，如图7 所示。密封固体变形计算模型应用Workbench Meshing 软件进行网格划分，其中密封片组和转子采用六面体网格，后挡板采用四面体网格，如图8 所示，密封片组区域进行网格加密。

图7 泄漏计算周期面网格Fig.7 Grid on the periodic surface of the leakage computational model

图8 有限元计算网格Fig.8 Grid of the finite element computational model

为提高计算结果的精度，需对泄漏流场与固体变形的计算网格进行独立性验证。如图5 所示，在密封片P1 的指尖靴前端取某一监测点A，分别以密封的泄漏量和点A 的变形量作为监测变量。网格独立性验证的计算结果如图9、图10 所示，当泄漏流场网格单元总数超过150 万时泄漏量基本稳定，当固体变形网格单元总数在3 万以上时点A 的变形量基本不变，因此确定泄漏流场网格单元总数为150 万，固体变形网格单元总数为3 万。

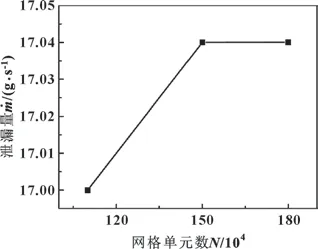
图9 泄漏计算模型的网格独立性验证Fig.9 Grid independence verification of the leakage computational model

图10 有限元计算模型的网格独立性验证Fig.10 Grid independence verification of the finite element computational model

3 计算结果与分析

3.1 迭代过程与收敛结果分析

以压差为0.1 MPa 时为例，对密封流动与变形的三维双向耦合迭代计算过程中的泄漏量、变形量、流固耦合面上的压力分布，以及计算收敛后泄漏流场的压力和速度分布结果进行展示并分析。需要说明的是第一次迭代计算所得的密封流场泄漏量及压力分布理论上与采用二维流场计算模型未考虑变形时的计算结果一致。

图11 给出了压差为0.1 MPa 时密封流动与变形双向耦合迭代计算过程中泄漏量及最大变形量随迭代次数的变化曲线。可见，与第一次迭代计算相比，第二次迭代计算得到的泄漏量明显增大，最大变形量减小。经第三次迭代计算后，泄漏量与变形量均达到收敛。迭代计算过程中泄漏量和最大变形量的数值及变化率如表1 所示，可以发现，第二次迭代计算的泄漏量相比第一次的增大了13.5%，最大变形量则减小了0.047%。第三次迭代计算的泄漏量与最大变形量相比第二次的分别变化了0.03%与0，均达到收敛标准。

表1 迭代计算过程中泄漏及最大变形的值Table 1 Values of leakage and maximum displacement in iterations

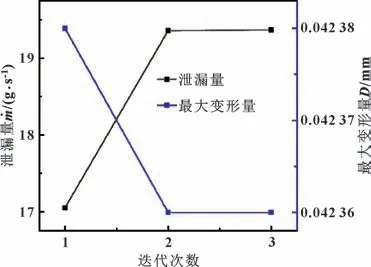
图11 泄漏及最大变形随迭代次数的变化Fig.11 Leakage and maximum displacement in iterations

图12 所示为压差为0.1 MPa 时三次迭代计算得到的流固耦合面F1 与F2 上压力分布。可见，随着迭代次数的增加， F1 面上压力先减小，后几乎不变，F2 上的压力数值则基本保持不变。

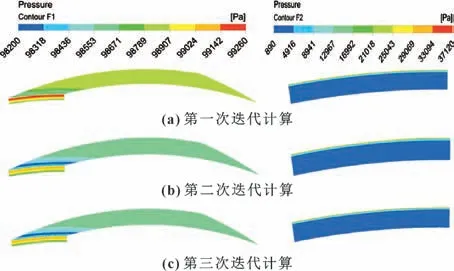
图12 迭代计算中流固耦合面F1、 F2 的压力分布Fig.12 Pressure distribution on F1 and F2 in three iterative calculations：（a） the first iteration；（b） the second iteration；（c） the third iteration

综上所述，压差为0.1 MPa 时，三维流动与变形双向耦合计算经过三次迭代达到收敛。这是因为第一次迭代计算中，密封结构受到流场的压力及转子离心膨胀的作用，产生了最大值为0.042 38 mm 的变形，此变形导致了第二次迭代计算泄漏流场及压力的变化；第二次迭代计算中泄漏流场产生的压差降低，密封变形也随之减小，变形量相对第一次迭代计算值仅降低约0.047%，无法对第三次迭代计算的泄漏流场产生显著影响。因此，经三次迭代计算后泄漏流场与固体变形达到稳定。

图13 所示为压差为0.1 MPa 时迭代计算收敛后泄漏计算模型周期面上的压力分布云图。可见，压降主要集中在密封片组靠近下游的一侧，尤其是后挡板保护高度以下的部分，大致对应密封的指尖靴区域，此处压力梯度很大。为便于分析泄漏流动的特性，取图6 中流体域内部垂直于转子周向的截面1，给出该截面上的速度分布如图14 所示。可见，上游气体进入前挡板与转子的通道后，由于通道突然减小，气体速度明显增大。在隔片下部区域，通道突然增大，气体在径向受到的阻力减小，因此气体的径向速度增大。但沿轴向，由于受到密封片组的阻碍，气体的轴向速度降低。气体进入密封片组区域后，由于阻力增大，速度随之下降，且泄漏气体主要被限制在后挡板保护高度区域流动，因此在密封片组区域的气体泄漏主要发生在指尖靴区域，而沿径向往外，气体速度逐渐变小，趋近于0。在进入后挡板与转子间通道后，由于阻力减小及通道收缩，气流速度再次增大。

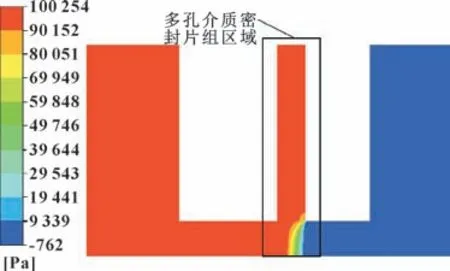
图13 泄漏计算模型周期面上压力分布Fig.13 Pressure distribution on periodic surface of the leakage computational model

图14 截面1 上的速度分布Fig.14 Velocity vector distribution on slice1

3.2 收敛后固体变形分布

压差设为0.1 MPa 时，迭代计算收敛后各密封片的变形量如表2 所示。可见密封片的最大变形主要取决于径向上的变形，而最大轴向变形的贡献较小。这一方面是由于密封片的指梁间留有变形的间隙，因此在径向容易发生变形，而在轴向上密封片组受到后挡板的支撑，不易发生形变；另一方面是由于转子离心膨胀的作用，在转子与密封片接触表面产生的径向力比轴向的压差作用力更大。

表2 密封片的变形Table 2 Displacement of the seal laminates

由于密封片的变形主要受径向变形的影响，故文中主要针对密封片的径向变展开分析。图15 给出了压差设为0.1 MPa 时密封片的径向变形分布，可以发现，三片密封片的变形规律相似：沿径向向外变形逐渐减小。这是因为密封片外环受到固支约束，指片类似于悬臂梁，与密封片外环相距最远的指尖靴前端变形最大，导致指尖靴前端翘起并脱离转子表面，仅指尖靴后半部分与转子表面接触，如图16 所示。三片密封片中P1 和P2 的最大径向变形值相近， P3 的最大径向变形值略大于P1 和P2，这是由于三片密封片的指尖靴与转子接触面的径向位移相等，而P3 的指梁部分直接与后挡板接触并受到两者间摩擦力的作用，于是P3 的指梁部分的径向位移在三片密封片中最小，则其指尖靴的径向变形最大，而指尖靴始终与转子保持接触，这就导致P3 的指尖靴前端翘起现象最为显著，其最大径向变形值也最大。

图15 密封片的变形分布Fig.15 Displacement distribution of laminates：（a） laminate P1；（b） laminate P2；（c） laminate P3

图16 指尖靴的变形Fig.16 Detail of the displacement distribution of the finger feet

3.3 压差对变形及泄漏的影响

设定压差分别为0.1、 0.3、 0.5 MPa，分析了上下游压差对密封结构变形及泄漏特性的影响。图17和图18 分别给出了压差为0.1、 0.3、 0.5 MPa 时计算收敛后密封片最大径向变形与最大轴向变形量。 3种工况迭代计算的收敛条件一致，均经过三次迭代计算达到收敛。可见，在0.1 ～0.5 MPa 范围内随着压差的增大，密封片的最大径向变形量变大，但增幅在2%以内，最大轴向变形则增大约400%。这是因为将三片密封片视作整体时，在压差的作用下，指梁径向位移受到了其与后挡板间摩擦力的约束，压差增大后，转子转速不变，其离心膨胀也不变，则指尖靴与转子接触面的离心膨胀径向位移几乎不变；但指梁与后挡板间的摩擦力增大，该摩擦力对指梁径向位移的限制进一步增强，使得指尖靴产生径向变形增大的趋势，但指尖靴又始终与转子保持接触，故导致指尖靴前端翘起，于是密封片最大径向变形量增大。此外，随着压差的增大，作用在密封片上的轴向力逐渐增强，因此密封片轴向变形呈线性增大。