厚度极化薄圆片压电换能器的瞬态响应

法 林,刘栋宁,梁 蕊,王宝妮,王艺美,史贵全,李玉霞,赵梅山

(1.西安邮电大学 电子工程学院,陕西 西安 710121;2.西安翻译学院 信息工程学院,陕西 西安 710105;3.中国石油集团测井有限公司,陕西 西安 710061;4.芝加哥大学詹姆斯·弗兰克研究所化学系,美国 伊利诺伊州 60637)

压电换能器是一种利用压电效应实现声能和电能之间相互转换的器件,被广泛应用于多种不同的领域中,例如,材料学科中的无损检测[1-4]、工程学科中的超声清洗[5-6]、食品行业的超声杀菌[7-9]和电子工程学科的无线通信[10-12]等。换能器的瞬态响应是衡量声波质量的一个重要指标,对换能器的瞬态响应进行研究是准确反演介质信息以及提高声学测量质量最基本的前提。

在以往的声学测量中,由于其复杂性,通常忽略激励信号与换能器能量转换的影响。如在声波测井和地震勘探领域中,人们通常使用理想模型描述声源信号[13-15]。在描述反演介质特性时,研究者通常会忽略换能器声-电转换的影响。由于换能器的机-电等效电路与激励信号频率有关,激励信号不同,换能器的机-电等效电路不同,测量声信号也不同,所以,不能忽略激励信号与换能器能量转换对测量声信号的影响。

考虑到激励信号与换能器能量转换对测量声信号的影响,拟研究厚度极化薄圆片压电换能器的瞬态响应。在经典压电换能器的机-电等效电路中引入辐射阻和辐射质量这两个力学变量,建立厚度极化薄圆片压电换能器的机-电等效电路,推导该压电换能器的电-声/声-电冲激响应和系统函数。考虑到辐射阻和辐射质量与频率有关,且在大多数声学测量过程中,激励换能器的电/声信号是包含许多频率分量的信号子波,进而将声学测量过程等效为一个并行传输网络模型。在此基础上对单频与多频信号激励下换能器的瞬态响应进行仿真与分析,测量声信号受到激励信号与能量转换的影响。

1 理论模型

图1为沿厚度方向极化的厚度极化薄圆片压电换能器模型示意图。图中,l和r分别为薄圆片换能器的厚度与半径。由于该换能器的厚度远小于和厚度垂直的径向尺寸,厚度方向的固有频率远大于径向方向的振动频率,所以,在厚度方向对薄圆片压电换能器施加电场时,可以近似认为压电换能器在与极化方向垂直的径向方向上来不及形变,处于夹持状态,只有沿厚度方向的应变不等于零。该换能器纵向压电方程[16]可以表示为

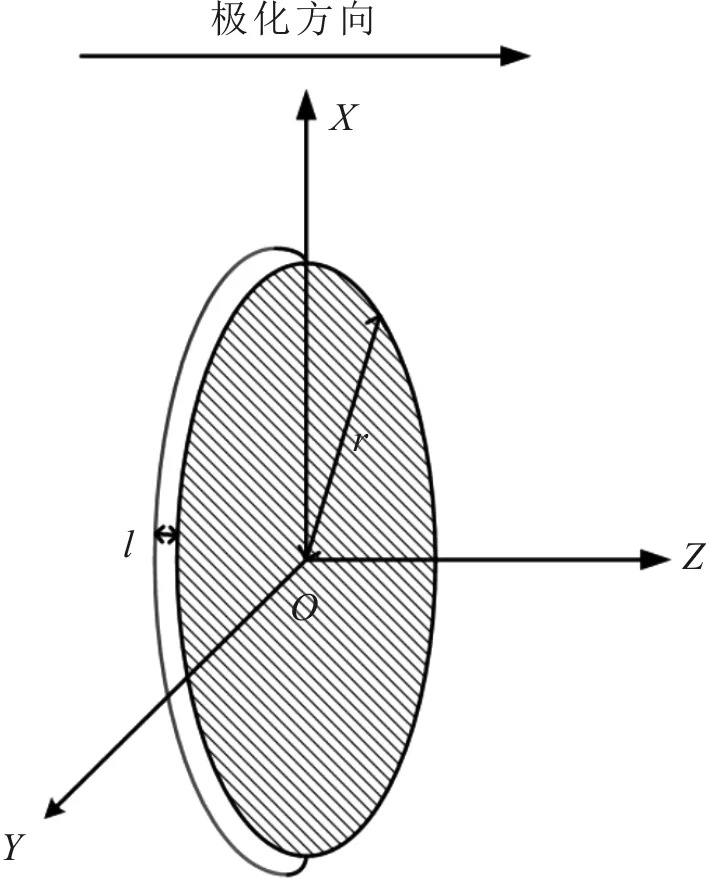
图1 厚度极化薄圆片压电换能器模型示意图

TZZ=CZZSZZ-hZZDZ

(1)

EZ=-hZZSZZ+βZZDZ

(2)

式中:TZZ表示沿厚度方向作用于换能器圆面的应力;EZ与DZ分别表示换能器厚度方向的电场强度分量和电位移分量;SZZ表示换能器在形变前后沿厚度方向的相对改变量;CZZ为沿厚度方向的弹性刚度常数分量,表示当SZZ发生单位变化时,TZZ的改变量;βZZ为沿厚度方向的介电隔离率分量,表示当DZ发生单位变化时,EZ的改变量;hZZ为沿厚度方向的压电劲度常数分量,表示DZ发生单位变化时,TZZ的改变量,或者表示SZZ发生单位变化时,EZ的改变量。

假设薄圆片换能器的绝缘性能良好,不存在自由电荷,则沿厚度方向振动的运动方程[16]可以表示为

(3)

式中:ρ表示换能器的密度;uZ表示厚度方向的质点位移分量;t表示时间;Z表示换能器沿厚度方向的变化量。

薄圆片体积为

V0=πr2l

则式(3)两边同时乘以薄圆片体积V0,可得

(4)

式中,m表示薄圆片压电换能器的质量。

当换能器工作在耦合液体中时,其受到的合外力F包含声场的反作用力Fr以及耦合液体的粘滞性引起的摩擦阻力Ff两个部分,则在时刻t,Fr、Ff和F的计算表示式分别为

(5)

(6)

(7)

式中:Rm表示摩擦力阻,其大小与换能器振动表面和耦合液体的接触面积大小有关;i为虚数单位;Rr表示换能器的辐射阻;Xr表示换能器的辐射抗。

换能器的辐射阻Rr和换能器的辐射抗Xr的计算表示式分别为

式中:ρ0表示耦合介质的密度;c0表示耦合介质中的声速;k表示耦合介质中的声波波数;S0表示声源表面积。

因为换能器的半径r远大于厚度l且侧面处于夹持状态,只有换能器的两个电极面产生振动,所以,声源表面积可以近似表示为

S0=2πrl+2πr2≈2πr2

当驱动电信号激励换能器时,除了受到自身产生的应力外,还受到合外力F的作用,其运动方程可以表示为

(8)

联立式(1)与式(2)得

(9)

将式(9)代入式(8),可得

(10)

薄圆片压电换能器满足几何方程

(11)

将式(11)代入式(10)中,得到时刻t薄圆片压电换能器在耦合液体中振动时的状态方程为

(12)

若薄圆片压电换能器的质点沿厚度方向做简谐振动,则质点在t时刻沿Z方向的位移可以表示为

uZ=u0ei(ωt-kZ)

(13)

式中:u0表示质点的初始位移;ω表示角频率。

将式(13)代入到式(12)中,得到时刻t薄圆片压电换能器沿厚度方向的质点位移表达式为

(14)

式中:Cm表示换能器的机械柔顺性;mr表示换能器的辐射质量。Cm和mr的计算表达式分别为

根据高斯定理,薄圆片换能器每个电极上的总电荷可以表示为

Q=∬DZdA=DZπr2

(15)

式中,A表示换能器某一电极面的面积,表达式为

A=πr2

联立式(2)和式(11)可得

(16)

时刻t的瞬时电流表达式为

(17)

式中:C0表示压电换能器的静电容;V表示施加在薄圆片换能器正负电极之间的电压;φ表示压电换能器的机电转换系数。C0、V和φ的计算表示式分别为

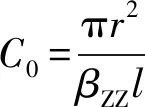
根据瞬时电流表达式建立换能器的机-电等效电路图。换能器的时域机-电等效电路如图2所示。换能器的s域机-电等效电路如图3所示。

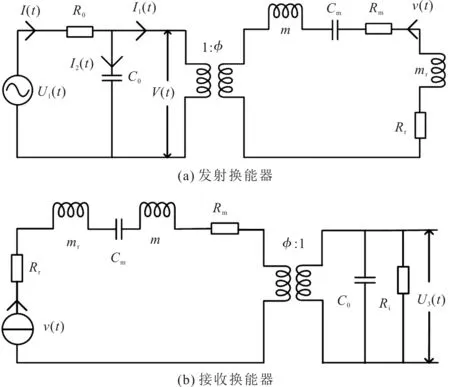
图2 换能器的时域机-电等效电路

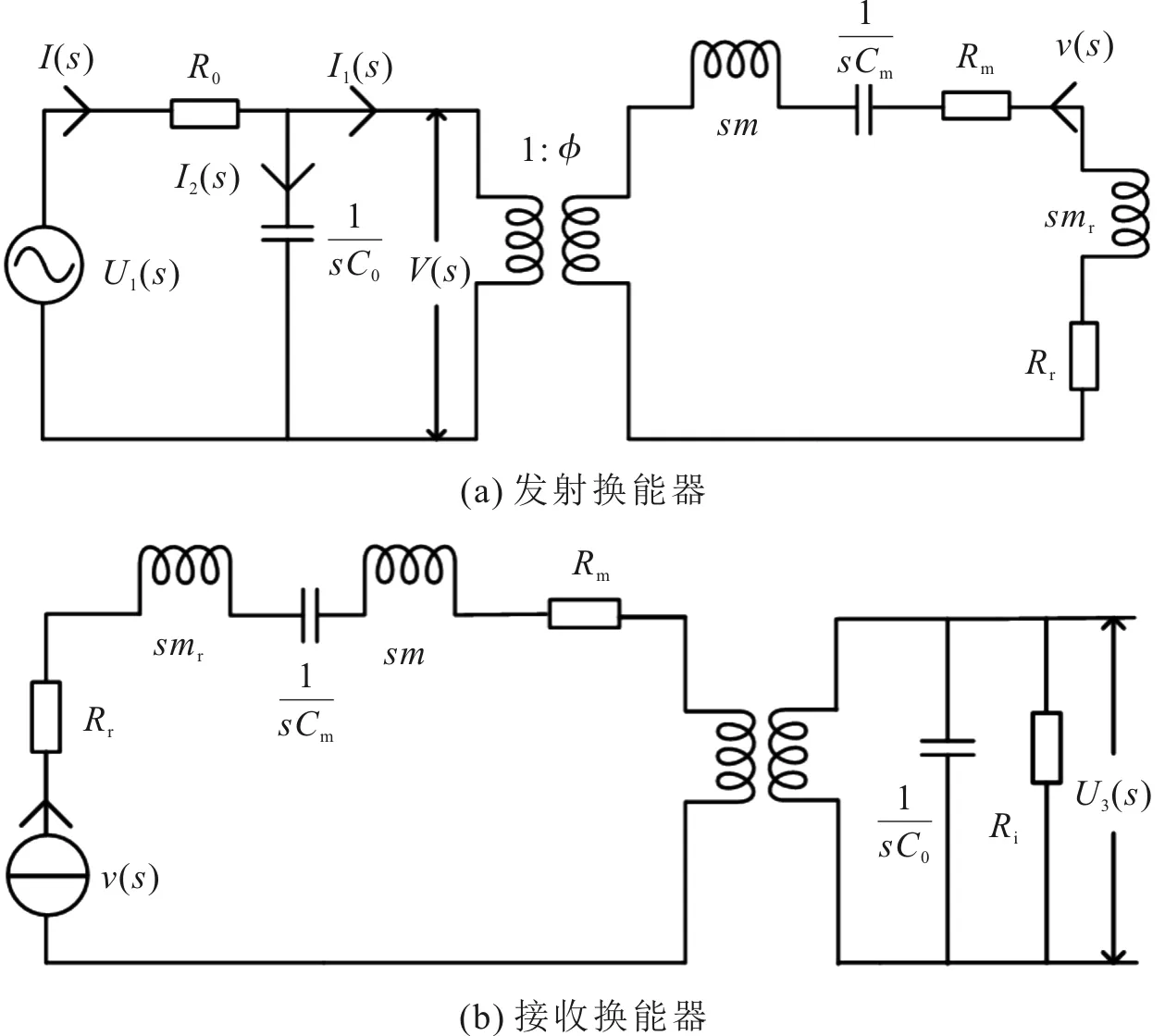
图3 换能器的s域机-电等效电路

图2(a)与图2(b)分别为发射换能器和接收换能器的时域机-电等效电路图,图3(a)与图3(b)分别为发射换能器和接收换能器的s域机-电等效电路图。图2中,U1(t)表示时刻t的驱动电压信号,v(t)表示时刻t换能器表面的质点位移速度,Ro为输出电阻,U3(t)表示时刻t接收换能器电端的输出电压信号,Ri表示输入电阻。图3中,s表示复频率,U1(s)、v(s)以及U3(s)分别表示时刻t换能器的s域驱动电压信号、质点位移速度以及输出电压信号。

与常规电路不同的是,换能器机-电等效电路图中的辐射阻、辐射质量的值均为频率的函数。根据图3(a)发射换能器s域机-电等效电路和基尔霍夫定律[17],可得

U1(s)=V(s)+I(s)Ro

(18)

I(s)=I1(s)+I2(s)=φv(s)+sC0V(s)

(19)

式中:I(s)、I1(s)和I2(s)分别表示图3(a)不同支路上的s域电流;V(s)表示换能器正负电极之间的s域电压。

将换能器的电-声转换系统函数定义为换能器s域表面振动速度v(s)与驱动电压U1(s)的比值,即

(20)

式中,R1=φV(s)/v(s)=s(m+mr)+(Rm+Rr)+1/sCm。

为了便于计算,令

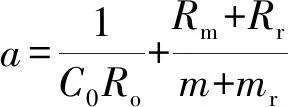
则可以将式(20)化简为

(21)

根据留数定理[18],讨论和求解发射换能器可能出现的3种运动状态所对应的电-声冲激响应方程组为

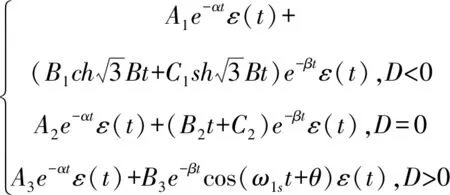
(22)

式中,

当换能器处于过阻尼模式D<0和临界阻尼模式D=0时,电-声冲激响应按指数规律呈非周期性衰减,不会向外辐射声波。当换能器处于振荡模式D>0时,电-声冲激响应由一个按指数规律衰减的直流项和一个振荡频率为f1s=ω1s/2π的阻尼正弦波组成,此时,换能器在驱动电压信号激励下,会向外辐射声波,是符合实际物理意义的解。

式(21)绝对可积,存在关系s=iω,则换能器的电-声转换系统函数可以被重写为

(23)

换能器声-电转换是电-声转换的逆过程,采用与发射换能器电-声冲激响应类似的求解方法,得到在振荡模式下,接收换能器t时刻的声-电冲激响应h3(t)和系统函数H3(iω)分别为

(24)

(25)

其中,

2 仿真与分析

在接下来的讨论和计算中,选择密度为856 kg/m、声速为1 424 m/s的变压器油作为换能器周围的耦合介质,压电材料选择压电元件(Piezoelectric Elements, PZT)PZT-5H,换能器的压电参数和几何参数如表1所示[16],使用Matlab进行仿真模拟。

表1 换能器的压电参数和几何参数

定义系统函数最大幅值处对应的频率是中心频率。根据式(23)与式(25)进行计算得到,发射换能器有负载时的中心频率为f1d=1.000 575 MHz,接收换能器有负载时的中心频率为f3d=1.005 189 MHz,发射换能器无负载时的中心频率f10=1.001 409 MHz,接收换能器无负载时的中心频率f30=1.006 017 MHz。

发射换能器和接收换能器的振荡角频率为式(23)与式(25)中的ω1s和ω3s,则振荡频率为f1s=ω1s/2π和f3s=ω3s/2π。经过计算,发射换能器无机械负载时的振荡频率为f1s0=1.002 307 MHz,接收换能器无机械负载时的振荡频率为f3s0=1.006 000 MHz。在有机械负载时,换能器的振荡频率fsd随施加在换能器上的正弦信号频率f的增加而逐渐趋近于空载中心频率,负载振荡频率与激励信号频率关系的仿真结果如图4所示。

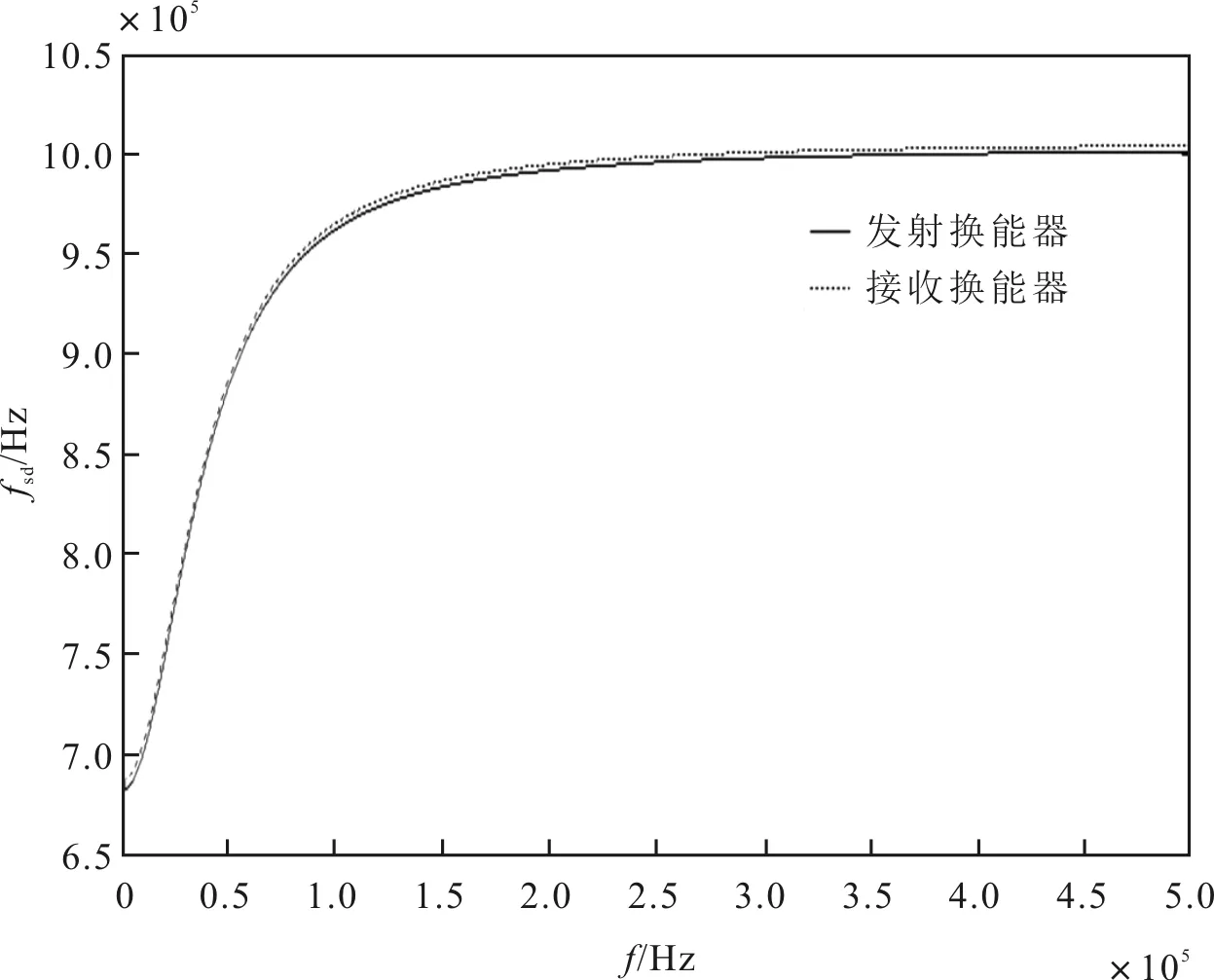
图4 负载振荡频率与激励信号频率关系的仿真结果

2.1 换能器电-声/声-电冲激响应

考虑到机-电等效电路图2中的辐射阻和辐射质量均为频率的函数,使用空载情况下发射换能器冲激响应的时域最大值h10max和频域最大值H10max对h1和H1n进行归一化处理,令

则发射换能器的电-声冲激响应仿真结果如图5所示。其中,图5(a)为发射换能器冲激响应归一化时域图,图5(b)为发射换能器冲激响应归一化幅度谱。

图5 发射换能器的电-声冲激响应仿真结果

采用空载情况下接收换能器冲激响应的时域最大值h30max和频域最大值H30max对h3和H3进行归一化处理,令

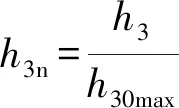
则归一化处理后接收换能器的声-电冲激响应仿真结果如图6所示。其中,图6(a)为接收换能器的归一化时域图,图6(b)为接收换能器的归一化幅度谱。

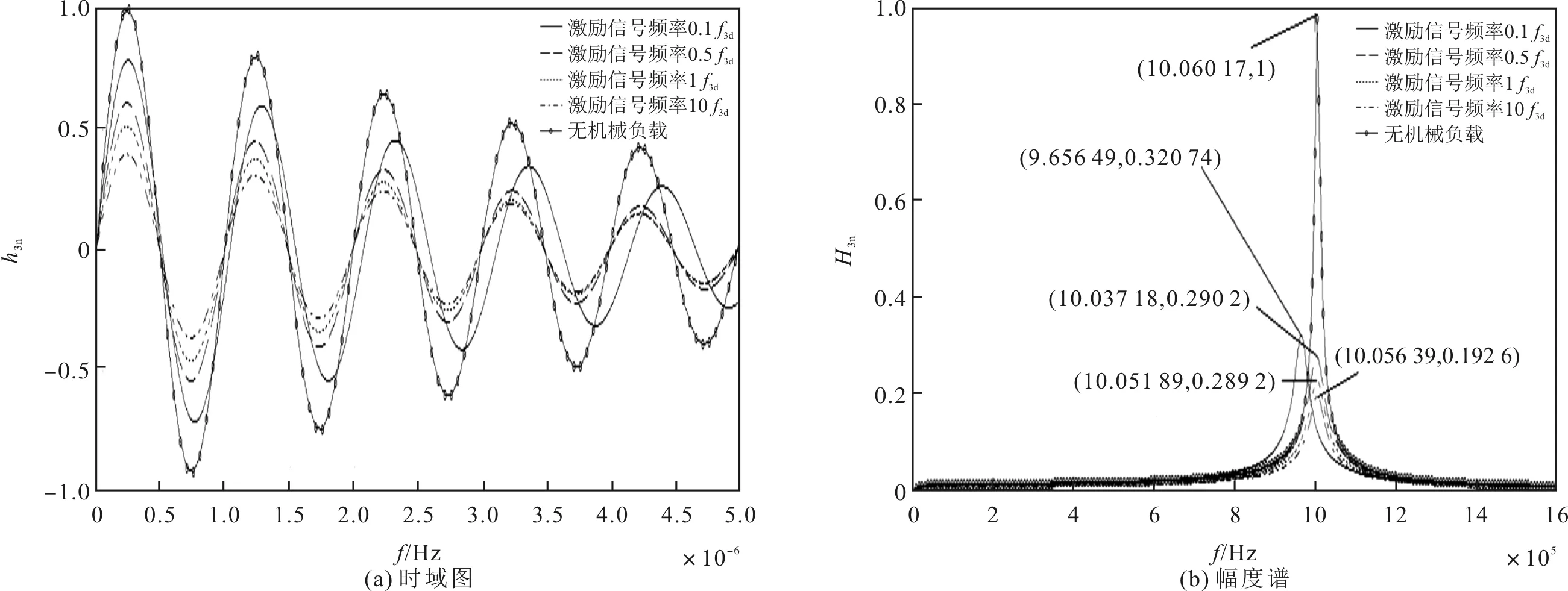
图6 接收换能器的声-电冲激响应仿真结果

从图5(a)和图6(a)可以看出,换能器冲激响应的幅值随激励信号频率的增大而减小。从图5(b)和图6(b)可以看出,换能器在无机械负载时的冲激响应中心频率不随信号频率的变化而变化;换能器在有机械负载时的冲激响应中心频率随信号频率的增大而增大,并逐渐趋近于换能器空载中心频率。另外,还可以看出,电-声冲激响应幅度谱带宽比声-电冲激响应幅度谱带宽要宽,即与发射换能器对驱动电压信号远离中心频率的频率分量的滤波作用相比,声-电转换对接收声信号远离中心频率的频率分量有更强的滤波作用。

2.2 正弦电信号激励下换能器辐射的声信号

选择幅度为1 V,频率分别为0.1f1d、0.5f1d、1f1d和1.3f1d的正弦驱动信号激励发射换能器,换能器振动速度v的幅度谱为VF,使用振动速度时域最大值vmax和频域最大值VFmax分别对v和VFn进行归一化处理,令

则正弦信号激励下换能器辐射声信号归一化时域图vn和归一化幅度谱VFn的仿真结果分别如图7和图8所示。从图7和图8的仿真结果来看,在正弦驱动电压信号激励下,换能器辐射声波信号会经历一个静止状态到稳态正弦振动的瞬态过程,幅度谱由稳态过程对应的脉冲与瞬态过程对应的平滑振幅曲线两部分组成。当正弦驱动电压信号频率等于负载中心频率时,发射换能器与正弦驱动电压信号发生共振,电-声转换效率最高,换能器电-声转换的频谱与驱动电压信号频谱叠加在负载中心频率处。当正弦驱动电压信号频率远离,即大于或小于换能器负载中心频率时,辐射声信号的幅值变小。

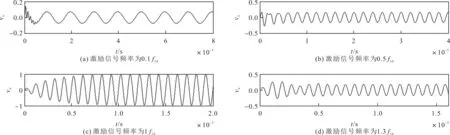
图7 正弦信号激励下换能器辐射声信号的归一化时域图

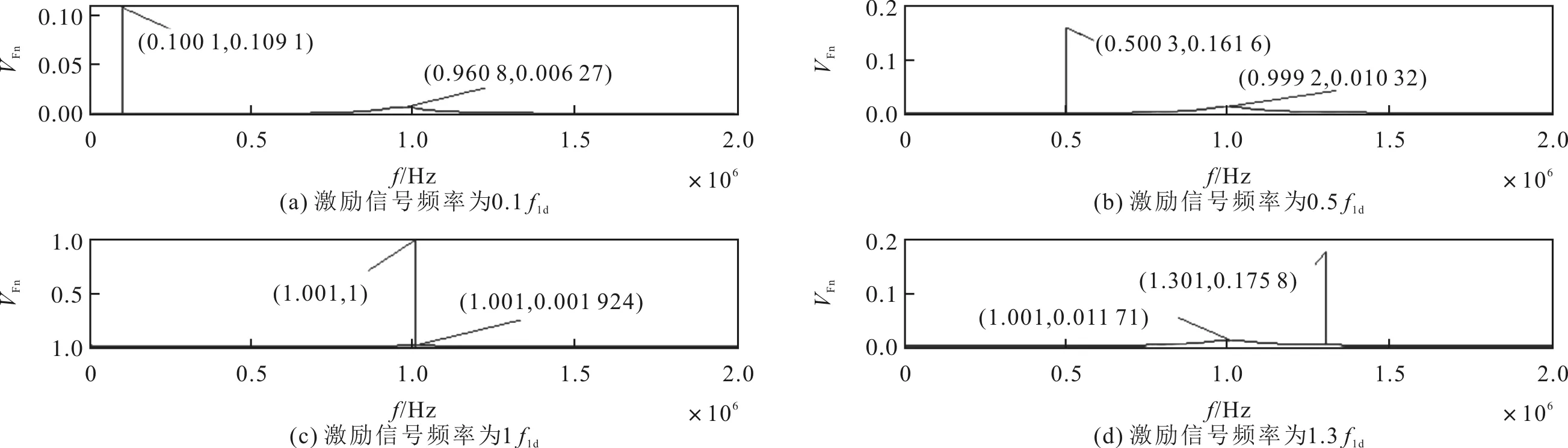
图8 正弦信号激励下换能器辐射声信号的归一化幅度谱

2.3 接收换能器输出端的电信号

虽然压电换能器的声-电转换是电-声转换的逆过程,但是,声-电转换和电-声转换并不完全相同,下面分两种情况来分析和讨论换能器的声-电转换过程。

2.3.1 正弦声波信号激励下换能器的测量电信号

选择幅度为1 V,频率分别为0.1f3d、0.5f3d、1f3d和1.3f3d的正弦声波信号激励接收换能器,分析换能器的声-电转换过程。接收换能器输出端电信号U3的幅度谱为U3F,采用测量电信号时域最大值U3max和频域最大值U3Fmax对U3和U3F进行归一化处理,令

则正弦信号激励下换能器测量电信号的归一化时域图U3n和归一化幅度谱U3Fn分别如图9和图10所示。

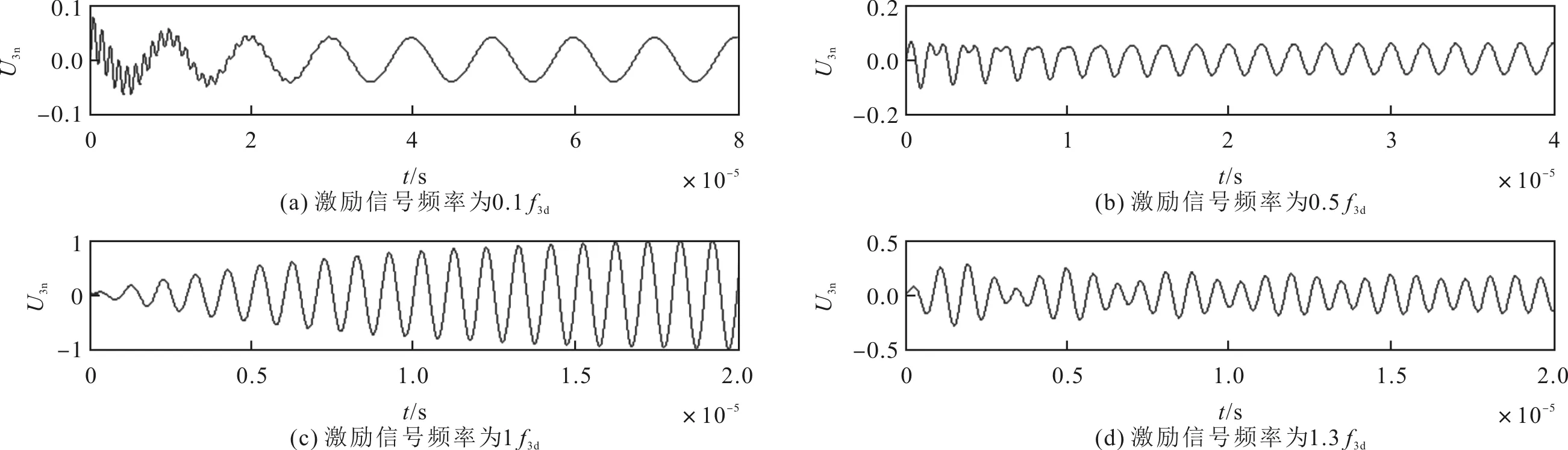
图9 正弦信号激励下换能器测量电信号的归一化时域图

图10 正弦信号激励下换能器测量电信号的归一化幅度谱

从图9和图10可以看出,与发射换能器辐射声波信号类似,接收换能器输出端的电压信号也存在一个由静态过渡到稳态正弦振动的瞬态过程。通过对比图7和图9发现,换能器声-电转换瞬态持续时间比电-声转换瞬态持续时间长,这是由于换能器声-电冲激响应幅度谱带宽比电-声转换冲激响应幅度谱带宽窄的缘故。

2.3.2 正弦信号转换后的测量电信号

将发射换能器和接收换能器放置在理想介质中,该介质的粘度和声衰减系数均为0,使发射换能器和接收换能器相距0.15 m。频率分别为0.1f1d、0.5f1d、1f1d和1.3f1d的正弦电信号经电-声转换和声-电转换后的测量电信号归一化时域图和归一化幅度谱分别如图11和图12所示。

图11 正弦信号经电-声和声-电转换后的电信号归一化时域图

图12 正弦信号经电-声和声-电转换后的电信号归一化幅度谱

从图11和图12可以看出,当正弦驱动电压信号的频率接近发射-接收换能器综合频响特性的中心频率时,接收换能器输出端电信号瞬态过程的振荡周期数最少,此时,正弦驱动电压信号的幅度谱叠加在发射-接收换能器综合频响特性对应的幅度谱上。当正弦驱动电压信号的频率远离发射-接收换能器综合频响特性的中心频率时,接收换能器输出端电信号从静止状态到稳定正弦振动状态的周期数增加,此时,时域波形和幅度谱的幅值减小。

2.4 复频电压信号激励换能器

在大多数声学测量中,激励发射换能器的驱动电压信号和到达接收换能器的声波信号都不会是简单的正弦驱动信号,而是复频信号。为此,在研究子波激励下换能器的瞬态响应时,同样不考虑传媒介质对辐射声波的影响,认为介质是理想弹性介质。

由于机-电等效电路中的辐射阻和辐射质量与频率有关,每个频率对应其特有的冲激响应。利用傅里叶变换,将激励信号分解为不同幅度、频率和相位的正弦分量,构建一种并行传输网络模型描述换能器的电-声和声-电转换过程。构建的并行传输网络模型如图13所示。图中,第Ⅰ部分为发射换能器的电-声转换过程,第Ⅱ部分为声波的传播过程,第Ⅲ部分为接收换能器的声-电转换过程。U1(t)表示驱动电信号,U1j为U1(t)的第j(j= 1,2,…,N)个频率分量;h1j(t,ωj)表示驱动电压信号的第j个正弦频率分量对应的电-声冲激响应;v1j表示被驱动电压信号的正弦分量U1j激励时的质点位移速率;v2jk表示将v1j的瞬态过程进行分解的第k(k= 1,2,…,M)个频率分量,即质点位移速度的第jk个频率分量;v2ωj为v1j的稳态正弦振动的频率分量,与U1j频率相同;h2jk(t,ωjk)、v3jk、h3jk(t,ωjk)和U3jk分别表示第j个瞬态过渡过程分解的第k个频率分量对应的介质的声脉冲响应、到达接收换能器的质点位移速度、声-电冲激响应以及测量电信号;h2ωj(t,ωj)、v3ωj、h3ωj(t,ωj)和U3ωj分别表示第j个稳态正弦振动对应的介质的声脉冲响应、到达接收换能器的质点位移速度、声-电冲激响应以及测量电信号;U3j为U1j激励下的接收换能器电端的电信号,U3(t)表示接收换能器电学端所有频率分量的累加。

图13 并行传输网络模型

模型中,驱动电压信号U1(t)的频率分量U1j(t)的计算表达式为

U1j(t)=|U1F(ωj)|cos[ωjt+φ(ωj)]

(26)

式中:ωj表示角频率;U1F(ωj)表示幅度谱;φ(ωj)表示相位谱。

时刻t驱动电信号U1(t) 的计算表达式为

(27)

图13中的第Ⅰ部分时刻t第j个等效电路的输出可以表示为

v1j(t)=U1j(t)·h1j(t,ωj)

(28)

时刻t发射换能器辐射声信号的表达式为

(29)

式中,v1j除了频率分量fj=ωj/2π外,还包含了与瞬态过程相对应的其他的频率分量。

若传媒介质为理想弹性介质,则换能器的冲激响应可以表示为

h2jk(t,ωjk)≡δ(t-t1)

(30)

式中,t1表示声波从发射换能器到接收换能器的传播时间。

时刻t到达接收器的声信号的第jk个频率分量可以表示为

v3jk(t)=v2jk(t)·h2jk(t,ωjk)

(31)

将时刻t第j个瞬态过渡过程分解为k个频率分量,其第k个频率分量对应的测量电信号表达式为

U3jk(t)=v3jk(t)·h3jk(t,ωjk)

(32)

图13第Ⅲ部分中,所有电路的累积输出,即接收换能器输出端电信号子波可以表示为

(33)

选择幅值为U0、角频率为ωg及时间窗为t0的门选正弦信号作为发射换能器的驱动电压信号,则时刻t的该驱动电压信号可以表示为

U1(t)=[H(t)-H(t-t0)]U0sin(ωgt)

(34)

式中,H(·)为Heaviside函数。

驱动电压信号频域表达式为

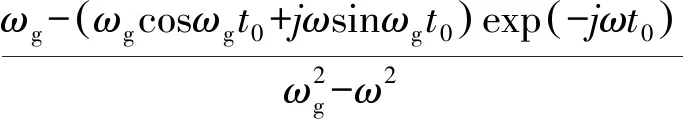
(35)

驱动电压门选正弦信号的图谱如图14所示。其中,图14(a)、图14(b)和图14(c)分别为驱动电压正弦信号的时域波形、幅度谱和相位谱,ωg=ω1d=2πf1d,t0=6π/ωg,U0=1 V。从图14(b)可以看出,幅度谱中幅值最大值处对应的频率略低于驱动电压信号频率,为0.983 2 MHz。

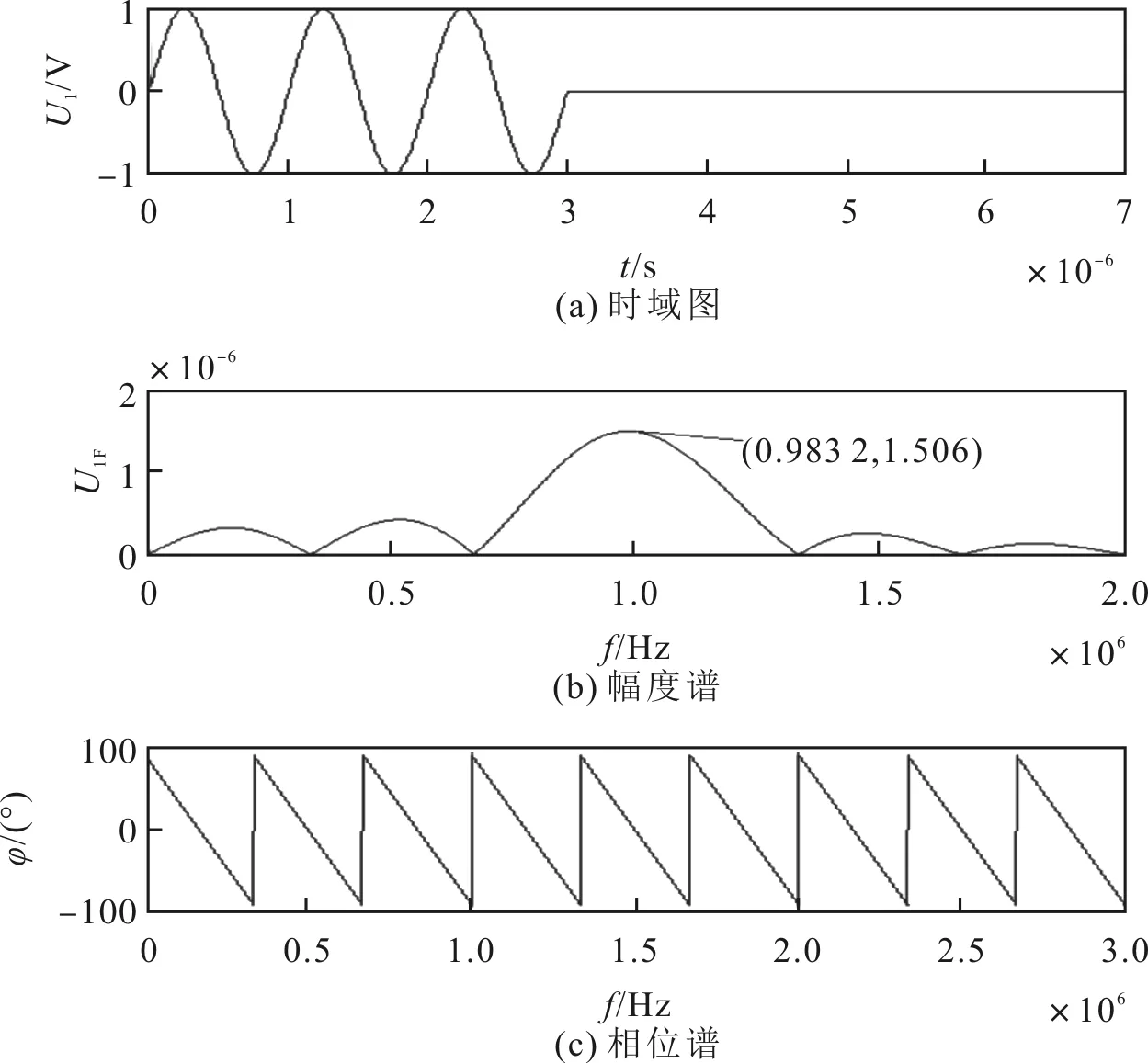
图14 驱动电压门选正弦信号的图谱

选择门选正弦信号分解的正弦频率分量作为独立信号源激励发射换能器,所选频率为0.4f1d、0.8f1d、1.2f1d和1.6f1d。发射换能器门选正弦信号频率分量激励下辐射声信号的质点位移速度如图15所示。

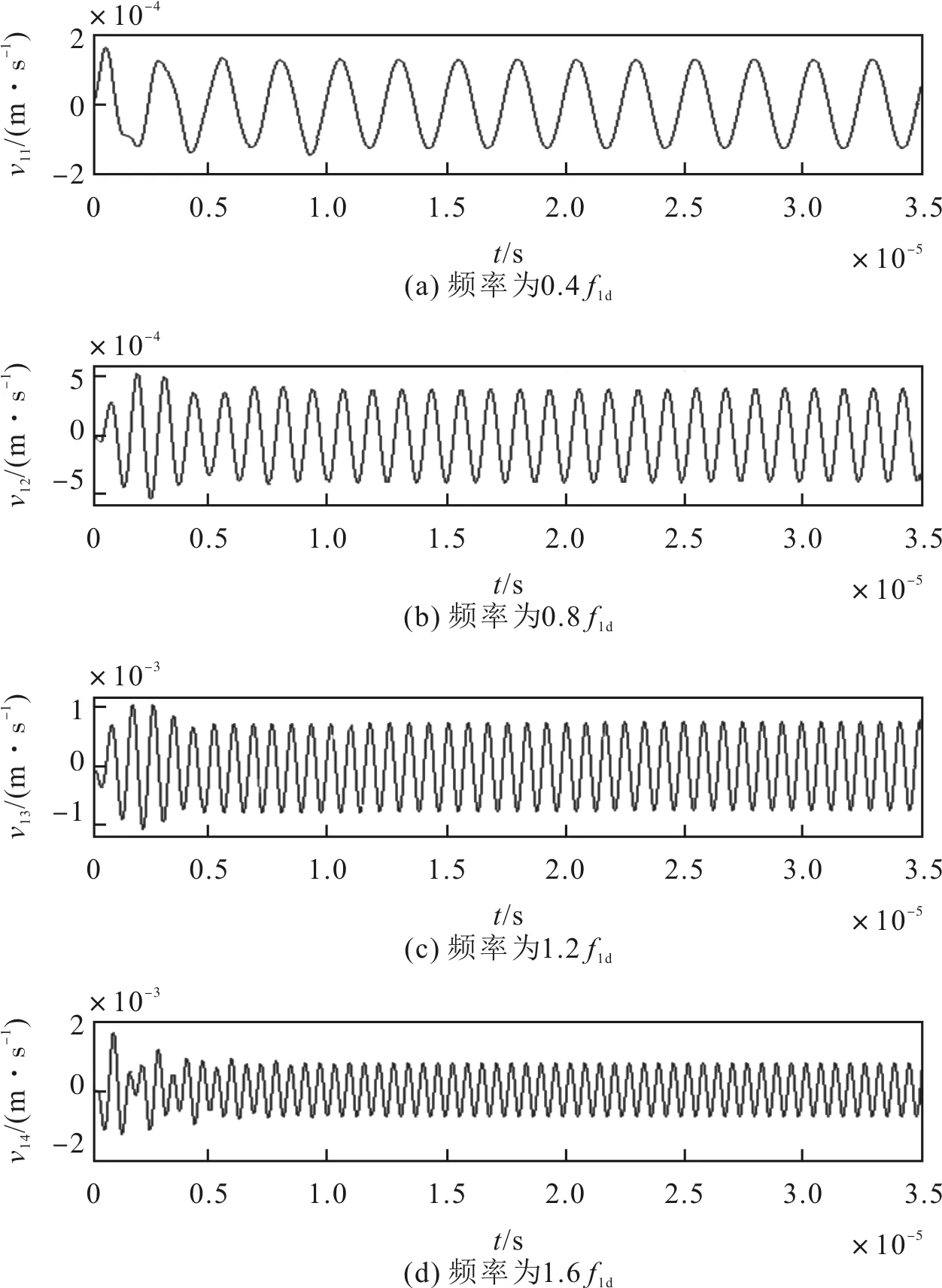
图15 门选正弦信号频率分量激励下的质点位移速度

采用门选正弦信号所有频率分量分别激励发射换能器,并将其向外辐射声波信号的累加输出进行归一化处理,门选正弦信号激励下的归一化质点位移速度如图16所示。其中,图16(a)和图16(b)分别为门选正弦信号激励下声波信号的归一化质点位移时域图和归一化幅度谱。

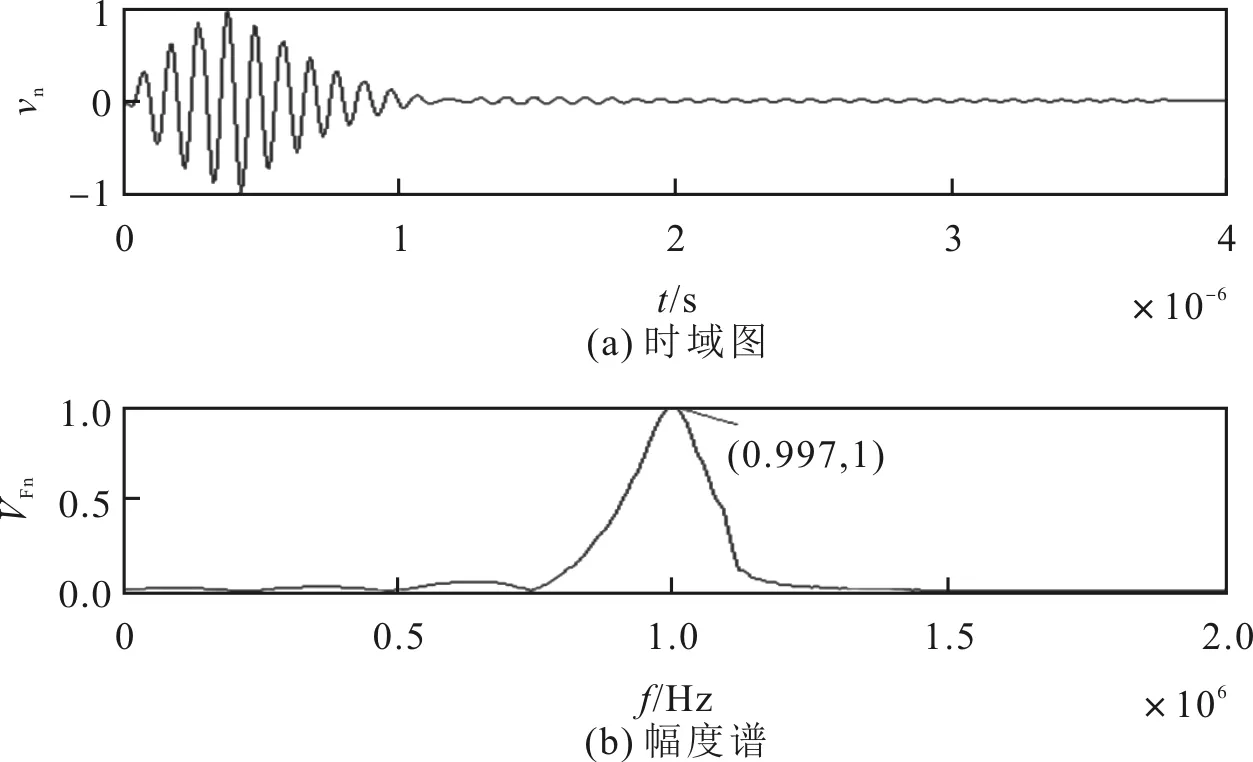
图16 门选正弦信号激励下的归一化质点位移速度

从图16的仿真结果可以看出,门选正弦信号激励下的辐射声波信号呈现出稳定的周期性振荡,其中心频率为0.997 MHz,略低于门选正弦驱动电压信号的中心频率。

接下来,将讨论电信号激励发射换能器向外辐射声波,以及声波在介质中传播后经接收换能器转化的测量电信号。设置发射换能器分别被频率为0.4f1d、0.8f1d、1.2f1d和1.6f1d的频率分量激励,门选正弦信号频率分量激励下的测量电信号波形如图17所示。

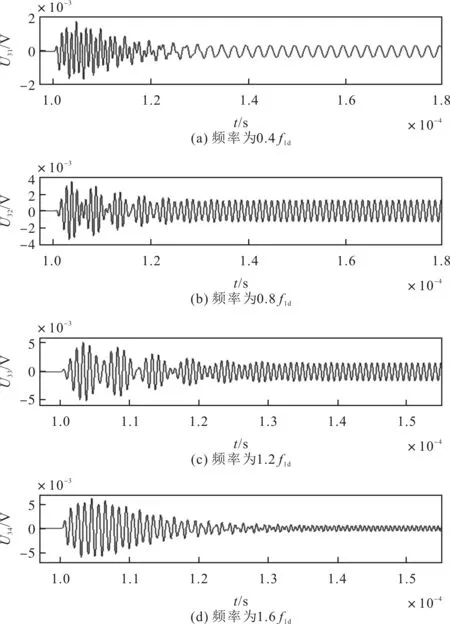
图17 门选正弦信号频率分量激励下的测量电信号

在门选正弦信号激励条件下,对接收换能器累加输出的测量电信号进行归一化处理,门选正弦信号激励条件下的归一化测量电信号图谱如图18所示。其中,图18(a)和图18(b)分别为接收换能器累加输出波形的归一化时域图与归一化幅度谱。

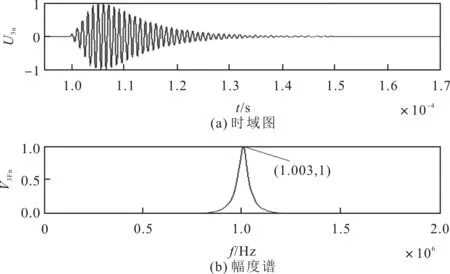
图18 门选正弦信号激励下的归一化测量电信号图谱

通过对比图16与图18可以发现,在门选正弦信号的激励下,接收换能器输出端电信号的瞬态过渡过程持续时间更长,时域波形更加无序,相应幅度谱带宽更窄,远离接收换能器中心频率的频率分量幅值显著减小或消失。由于接收换能器对接收到的声信号具有声-电滤波作用,因此,导致接收换能器输出端的电信号中心频率为1.003 MHz,略高于发射换能器辐射声信号的中心频率。

3 结论

在运动方程与压电方程的基础上,推导了厚度极化薄圆片压电换能器的电-声/声-电冲激响应及传输函数,建立了发射/接收换能器的机-电等效电路。分析了在正弦信号激励下,发射换能器辐射的声信号与接收换能器输出端的电压信号波形特征。考虑到辐射阻和辐射质量是频率的函数,将机-电等效电路模型扩展为一个并联传输网络模型,以描述多频信号激励下的电-声和声-电转换过程,并选择门选正弦信号作为激励信号,对并联传输网络模型的输出结果进行仿真分析。

通过计算、推导和分析,得出以下几点结论。

1)当换能器的几何参数与压电参数确定后,空载振荡频率与空载中心频率不随激励信号频率的改变而改变。相比之下,换能器负载振荡频率和负载中心频率随激励信号频率的变化而变化。

2)换能器的电-声/声-电冲激响应与激励信号频率有关,冲激响应幅值随信号频率的增加而降低,中心频率随信号频率的增大而逐渐趋近于换能器的空载中心频率。

3)由于惯性的存在,在正弦信号激励下,换能器的输出声/电信号存在一个从静止到稳定的正弦振动瞬态过程,其幅度谱由稳态过程对应的脉冲以及瞬态过程对应的连续平滑的振幅曲线两部分组成。

4)门选正弦信号激励下换能器的输出波形呈现稳定的周期性振荡,接收换能器输出端电信号的振荡持续时间比发射换能器辐射声波信号的振荡持续时间长。