粘性Cahn-Hilliard方程的二阶凸分裂有限元格式

苗妮,张建文,王旦霞

(太原理工大学数学学院,山西 晋中 030600)

1.引言

Cahn-Hilliard方程最初由Cahn和Hilliard在非线性系统的二元混合物中用来描述相的分离和粗化现象[1],后来在材料力学领域中也有很广泛的应用[2−3].

粘性Cahn-Hilliard方程是在经典Cahn-Hilliard方程中添加了粘性项βut,其中β >0.它是由Novick-Cohen提出来的一种具有慢松弛变量的相分离耦合的连续模型,近来在流体动力学中引起了更多的关注.本文研究的粘性Cahn-Hilliard方程[4]如下:

其中u表示浓度场,ϵ是一个与平衡界面厚度有关的正数,w代表化学势能,β是粘性系数,Ω ⊂Rd,边界∂Ω满足利普希茨条件,n是边界∂Ω上单位外法向量,f(u)=(u2−1)u是双阱势函数F(u)=的导数.Cahn-Hilliard方程总能量可以记作

Cahn-Hilliard方程是一个非线性的抛物型偏微分方程,在数值实验中,处理扩散项和非线性项非常困难.为了解决上述问题,半隐方法[5]被提出,即方程中的线性项被隐式处理,非线性项被显式处理,但它的稳定性不是很好,往往需要很小的时间步长.为了加快计算的速度,不变能量二次化(IEQ)方法[6]和标量辅助变量(SAV)方法[7]被提出,但是又需要引入更多的辅助变量.后来Eyre提出了一种凸分裂方法[8],即对于凸的部分作隐式处理,对于凹的部分作显式处理,这样得到的格式是能量稳定的,但是它在时间上是一阶精确的.近年来二阶精确(时间)的数值格式受到了极大的关注,然而,二阶格式的研究却很少.因此,结合凸分裂方法,本文对粘性Cahn-Hilliard方程提出了二阶数值逼近,对时间导数采用二阶向后差分(BDF)格式.

本文内容安排如下: 第2节给出粘性Cahn-Hilliard方程的弱形式和离散格式;第3节证明了格式的能量稳定性;第4节,给出有限元解误差估计的理论分析;第5节,通过时间收敛阶、空间收敛阶和相分离的数值算例,验证了格式的收敛性和有效性;第6节,进行了总结.

2.离散格式

3.稳定性分析

在这一节,将对提出的全离散格式进行稳定性分析.

凹的部分写成

利用Cauchy-Schwarz不等式得

结合上述式子,当0<τ <2ϵ2时,得到

根据自由能的定义(3.1),则定理得证.

推论3.1设Ξn ≤C0,存在常数C >0,有下面的估计式成立

证对任意的n,将(3.2)式从1到N −1求和有

则估计式证毕.

接下来,对n=1时刻的全离散格式(2.6)进行稳定性分析.

则对任意的τ、ϵ>0,满足如下的能量耗散定律

将(3.17)和(3.18)相加得

利用下面的等式

对于凸的部分得

对于凹的部分可以推出

结合以上等式得到

根据自由能的定义(3.15),则定理得证.

4.误差估计

在本节,将对全离散格式(2.5)进行误差估计的理论分析.首先做出如下正则性假设

为了之后证明的简便,引入下面的记号

首先,引入下面定义和引理.

定义4.1H−1的范数定义如下

引理4.1Ritz投影满足

若p=q=2,则称为Cauchy-Schwarz不等式.

引理4.3(离散的Gronwall不等式) 设C0,∆t是正数,且ak,bk,ck,dk满足下面条件的非负序列

接下来,将进行误差估计的分析.

根据Ritz投影和离散拉普拉斯算子∆h,得

接下来依次估计Ji.对于J1,根据Cauchy-Schwarz不等式和Young不等式得

对于J2,根据Cauchy-Schwarz不等式和Young不等式得

对于J3,根据Cauchy-Schwarz不等式和Young不等式得

对于J4,根据Cauchy-Schwarz不等式、Young不等式和引理4.1得

对于J5,根据Cauchy-Schwarz不等式和Young不等式得

对于J6,根据三角不等式得

接下来我们对I1-I4进行估计.对于I1,根据Cauchy-Schwarz不等式、Young不等式和引理4.1得

对于I2,根据Cauchy-Schwarz不等式、Young不等式和引理4.1得

其中C1是与h和τ无关的正常数.对于I3,根据Cauchy-Schwarz不等式和Young不等式得

对于I4,根据Cauchy-Schwarz不等式和Young不等式得

其中C2、C3是与h和τ无关的正常数.将I1-I4全部相加得

结合上述不等式得

5.数值算例

在这一节,采用一些数值算例来验证格式的收敛性和可靠性.在下面的模拟中,均采用P2有限元空间,使用软件Freefem++进行数值模拟[9].

表5.1-5.3给出了H1范数下的误差和空间收敛阶,初始条件为u=cos(πx)cos(πy).参数采用ϵ=0.01,0.05,0.10,β=0.1,1.结果证明的空间收敛阶趋于2.我们也给出不同参数ε,β对误差和收敛阶影响的结果.

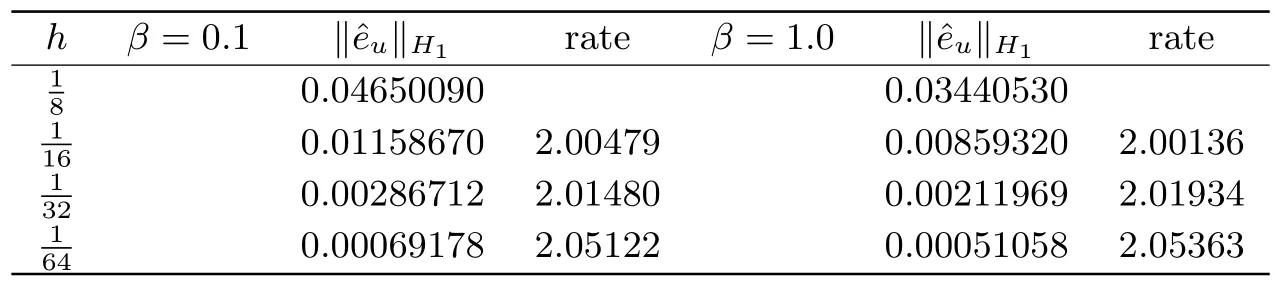
表5.1 误差和空间收敛阶:ε=0.01

表5.2 误差和空间收敛阶:ε=0.05

表5.4 误差和时间收敛阶:ε=0.01

表5.5 误差和时间收敛阶:ε=0.09

表5.4-5.6给出了H1范数下的误差和时间收敛阶,初始条件为u=0.2 sinxsiny,参数采用ϵ=0.01,0.09,0.10.结果表明‖‖H1的时间收敛阶都趋于2,我们也给出不同参数下ε,β对误差和收敛阶影响的结果.

最后,为了更好的观察数值解的变化过程,在本实验模拟了粘性Cahn-Hilliard方程的相分离过程,如图5.1-5.6,计算区域在[0,1]×[0,1],参数ϵ=0.1和β=1.初始条件取随机值u=2rand()−1,其中rand∈[0,1].

图5.1 T=0.001

图5.3 T=0.05

图5.4 T=0.1

图5.5 T=0.3

图5.6 T=2

6.总结

本文主要提出了一种基于凸分裂方法的粘性Cahn-Hilliard方程二阶向后差分格式(BDF)的数值逼近,然后进行了能量稳定性和收敛性的理论分析,最后进行了一些数值算例验证了格式的可靠性.