基于流固耦合理论的山区房屋洪水响应分析

2023-06-29余劲松安浩然郭来栋

四川建筑 2023年2期

余劲松安浩然郭来栋

以某3层框架结构为研究对象，基于流固耦合分析理论，采用ANSYS构建了山洪与结构的耦合分析模型，分析结构在不同深度洪水冲击时的响应情况，同时比选分析了“过流堰”防护措施、短柱扰流防护措施下结构的响应情况。研究结果表明：山洪冲击结构时，水深未达到底层楼面时，结构位移及应力均较小，满足结构安全要求，到达楼面板后，结构最大应力突增，迎水侧底层柱柱底混凝土开裂；“过流堰”防护措施可以显著降低结构稳定绕流阶段的稳定位移，但应力降低不明显，迎水侧混凝土仍有开裂风险；短柱扰流防护措施能够降低结构应力，满足结构安全要求，可以考虑在山区新建房屋时采取此种方式。相关经验可供类似山区低层框架结构抗洪设计借鉴。

洪水冲击；山区房屋；流固耦合；动力响应；防护措施

TV131.2 A

［定稿日期］2022-03-31

［作者简介］余劲松（1996—），男，碩士，研究方向为桥梁防灾减灾。

洪涝是因降雨、融雪、冰凌、溃坝（堤）、风暴潮、热带气旋等造成的江河洪水、渍涝、山洪、滑坡和泥石流等，以及由其引发的次生灾害。山洪灾害是我国洪涝灾害引起的主要次生灾害，危害极大，2020年，全国（港澳台除外）因洪涝受灾7 861.5万人次，倒塌房屋9.0万间，造成直接经济损失2 669.8亿元［1］。山洪具有突发性强、破坏力大、难以预警、发生在偏远山区等特点。国内外学者对山洪及其引起的次生灾害进行了大量研究，除了对暴雨山洪的形成原因和演进规律进行研究外［2-5］，也有学者对洪水、泥石流等对结构的影响，及其防治措施进行了研究。肖诗云等［6-10］通过水槽试验，研究了到溃口不同距离、不同墙体开洞率下的山区乡村房屋抗洪能力。杨哲豪等［11-12］建立了数值模型研究溃坝洪水对结构物的冲击荷载。王友彪等［13-15］通过水槽试验和数值模拟的方法，以流深和流速作为主要研究参数，研究了洪水、泥石流对桥墩的影响。桥梁工程中，常采用设置扰流短柱的方式减小洪水对桥墩基础的冲刷和冲击［16］。而目前针对山区房屋防山洪的工程措施的研究还很少［17-18］。

目前，对于桥梁、大坝等结构在洪水或泥石流作用下的动力响应研究水平不断提高，研究内容也不断深入，但对于山区房屋，研究相对滞后。在我国西部山区，山洪影响更为突出，山区房屋多为低层，常采用整体框架的结构形式。在地质灾害多发地，房屋常面临洪水和泥石流的威胁，因此研究低层框架结构在山洪冲击作用下的动力响应很有必要。

本文依托某洪水易发地3层框架结构民房开展研究，结构首层层高4 m，2～3层层高3 m。为确保该房屋在洪水冲击作用后的正常使用，保障人民生命财产安全，本文通过数值模拟计算，研究在一定洪水流速冲击作用下，不同水深工况下洪水对结构的影响，通过分析结构的位移及应力，提出合理的防护措施，以期对相似民建工程提供参考。

1 流固耦合模型与方法

1.1 原理

山洪冲击房屋属于流固耦合作用问题，即建筑结构在流场作用下的振动和变形会反过来改变流场，改变后的流场又反作用于结构，导致结构的荷载幅值及分布发生改变。流固耦合过程中结构的动力学控制方程基于达朗贝尔原理（DAlemberts principle）见式（1）。

［M］{}+［C］{a·}+［K］{a}={P（t）}（1）

式中，［M］为结构质量矩阵，［C］为阻尼矩阵，［K］为刚度矩阵；{}、{a·}、{a}分别为结构的加速度、速度及位移；{P（t）}为结构所受合力，t为结构与流体耦合时间参数。

流体介质控制方程为质量守恒方程、动量守恒方程和能量守恒方程。其通用形式表示为式（2）。

（ρφ）t+（ρuφ）x+（ρvφ）y+（ρwφ）z=

xΓφx+yΓφy+zΓφz+S（2）

式中：t是时间；φ是通用变量，例如，表示为质量守恒方程时取1，表示动量守恒方程时取速度量；u、v、w分别表示速度矢量在x、y、z方向的分量；ρ为计算域流体密度；Г为广义扩散系数；S为广义源项。

以水作为流体介质，考虑其为黏性不可压缩流体，不考虑热量交换。采用有限体积法对控制方程和流体区域进行离散，结构域和流体域的计算结果通过流固耦合面互相传递。待当前时刻的计算结果迭代收敛后，进行下一个时间步的计算。具体计算过程通过调用ANSYS- FLUENT的瞬态计算模式实现。

1.2 数值模型

分析对象为3层框架结构，如图1所示。首层层高4 m，2、3层层高3 m，楼板厚度0.1 m，立柱0.4 m×0.4 m，梁高0.5 m、宽0.3 m。梁板柱均采用C30混凝土，抗拉强度ft=1.43 MPa，弹性模量E=3×104 MPa，泊松比μs=0.18，容重G=23 kN/m3。混凝土本构关系采用FLUENT默认本构。山区洪水含沙量较大［12］，会少量增加水的密度及黏度。本模型忽略含沙量对洪水的影响，采用黏性不可压缩的清水作为流体材料。密度ρ=1000 kg/m3，动力粘度μ=1.003×10-3 Pa·s。

设置洪水流域为矩形断面，为减弱计算域壁面对模型流场的影响，设置计算域宽20 m、长50 m，高为h （h=1～4 m），同时设置边界层10层，每层5 mm；河流洪水流速范围一般为4～15 m/s（这是对于常规河流流域洪水而言，河流断面常呈“V”型，河流宽度通常在20～50 m），对于山区聚居地，山洪演进过程中，洪水断面更大，能量被地表植被、低矮建筑耗散较大，且山区山谷交错。因此，山洪洪峰到达民建建筑时其能量已大幅减少，在冲击结构时流速相对于河流流速较小，故偏危险的将其流速考虑为4 m/s。设置进口（inlet）边界为速度条件4 m/s；地面、侧面及流固耦合面设置为壁面（Wall）；顶面及出口设置为开放边界（Opening）且相对压强为0。流固耦合模型如图2所示。

数值计算采用标准k-epsilon两方程模型，近壁面函数采用标准壁面函数。

2 计算结果分析

2.1 结构响应分析

在一定流速下，洪水冲击结构的位移、应力响应与水位有关。入口流速恒定为4 m/s，计算域水深为1～4 m，得到结构承受的冲击力时程曲线、上游侧柱底迎水面正应力时程曲线及底层柱柱顶位移时程曲线，如图3～图5所示。

流体冲击结构一般可分为瞬时冲击、减速衰减、稳定绕流3个阶段。如图3所示，水深为4 m时，结构所受冲击力在0.2 s内从A点的0迅速增加到B点的398.7 kN，结合图4、图5亦可发现该阶段的结构应力及位移响应值迅速增大，为瞬时冲击阶段。此外，水流与结构物接触的瞬间，速度变化率达到最大值，故其冲击力达到最大值。在B点到C点间，不难看出其冲击力逐渐衰减，图像均呈下凹状，冲击力衰减速率降低，冲击力平均衰减速率为64.13 kN/s，在B点时结构的自身能量（势能）达到最大值，因此结构出现回弹，位移减小，做往复运动，出现振动现象。由于结构与流场的流固耦合作用，水流会耗散结构的弹性势能及动能，对其产生阻尼力，随着结构总能量的减小，这种阻尼力也随之减小，因此结构响应在峰值点后呈现减速衰减的现象。C点过后，当结构最终动能及势能被水流耗散，结构自身产生一个基本稳定的变形，其回弹力与水流冲击力平衡，该阶段为稳定绕流阶段。在本模型中，最大变形值仅为0.21 mm，因此不采用位移作为结构安全评估因素。

由图4～图6可知，水深为1～3 m时，结构最大应力出现在上游侧柱底迎水面，分别为0.05 MPa、0.27 MPa、0.58 MPa，最大位移分别为0.005 mm、0.072 mm、0.210 mm。当水深为4 m时，结构最大位移、应力分别为0.157 mm、2.12 MPa，结构最大拉应力出现在上游侧柱底迎水面，此工况下上游侧柱底稳定绕流下的拉应力（1.68 MPa）大于混凝土抗拉强度设计值，柱底出现拉裂缝。不难看出，水深为4 m时结构应力响应较3 m水深大1.54 MPa，但其最大位移响应小于3 m水深时结构最大位移，2个工况在稳定绕流阶段的位移响应值接近。通过分析认为，当洪水洪峰冲击到柱迎水面及楼面板的瞬间，接触面水流流速突变为0，其加速度达到最大值，结构产生最大响应，该阶段为瞬时冲击阶段。洪水冲击楼面板，楼板会增大结构的抗侧力刚度，直接导致结构的顺流向位移降低，楼板具有较大的阻水面积且竖向刚度较低，导致其产生向上的位移，洪水对面板有一个向上的举托力，楼面板产生向上翘曲，最大位移出现在楼面。同时，该举托力导致柱底拉应力加大，限制了结构沿水流方向的位移，因此水深4 m时结构应力较大，位移却较小。

综上所述，在一定的流速下，当水深低于首层楼面高度时，结构所受的冲击力和位移响应都随着洪水深度的增大而增大。当水深达到首层楼面高度，洪水直接作用于梁和楼面板时，结构受到的冲击力急剧增加，上游侧柱底处的应力也大幅增加。但是由于楼面板对水流的影响，结构的位移响应较小。可以看出，在保证结构安全性的基础上，适当增加结构首层层高，可以避免结构薄弱位置出现较大拉应力，有助于防止该处混凝土出现拉裂缝。

2.2 结构表面冲击荷载分析

研究结构受到最大冲击力时，提取上游侧底层中柱迎流面压应力分布，如图7所示。

从图7容易看出，h=1～3 m时，洪水对柱体的最小冲击压力均出现在h处，最小冲击压力分别为 1 621 Pa、1 643 Pa、1 690 Pa，随着洪水深度的增加，其对结构的最小冲击压力虽有增长，但增加幅度不大，基本保持不变。h=1～3 m时，水对柱体的最大冲击压力出现在约0.5h的位置，分别为5 400 Pa、5 950 Pa、6 100 Pa。同樣的，随着洪水深度的增加，其对结构的最大冲击压力的增加幅度不大。

h=4 m时，3 m以下的柱表面冲击压力在1 000 Pa左右，大于3 m时，随着高度的增加，柱表面所受冲击压力持续增加，最大冲击压力出现在柱子最高处约为3 448.1 Pa，较其余3个工况小。分析其原因，水深h=4 m时，洪水已经淹没底层楼面，楼面和梁分担了部分洪水冲击力。同时由于楼板的阻水效应，导致部分水流回流，与来流的动能相互抵消，因此其柱子的最大表面冲击压应力和最小表面冲击压应力均较小。

综上所述，当洪水水深低于楼面板板高度时，柱体表面所受的冲击压力分布呈倒“C”型。最小冲击压力出现在水深高度处，最大冲击压力出现在0.5倍水深处。而且洪水水深对冲击压力的最大值、最小值影响较小。当洪水水深刚刚漫过楼面板时，靠近水面部分的柱体表面所受的冲击压力较大，其余部分冲击压力较小，分布也较均匀。

3 山洪防护措施分析

由前文可知，当水深h=4 m时，结构最大拉应力为2.12 MPa，稳定绕流阶段的拉应力为1.67 MPa，都出现在迎流侧柱底，均超过混凝土抗拉强度设计值1.43 MPa。因此，将针对水深h=4 m的情形，对该3层民用建筑进行了山洪防护设计。

3.1 防护措施

山洪防护措施主要包括非工程措施和工程措施［10］。非工程措施包括调查评价、监测预警系统、群测群防体系及加强山丘区人员搬迁管理，为主要防护措施。工程措施为被动防护方式，采取护岸、堤防，河道护底、跌水等消能措施，但此类防御措施范围广、投资大，且在水流长期作用下防护结构容易出现基底脱空，混凝土断裂，结构冲毁等问题。因此，一种简单、高效、投资小的防护措施对改善山区山洪冲击影响具有积极意义。

本文提出2种适用于普通民宅的洪水防护方式——增设小型“过流堰”或短柱，如图8所示。因山村地区部分民宅门外会修建一个小斜坡，以保证室内外高差来防潮。当洪水冲击时，若漫过斜坡，该斜坡即为过流堰，第一种洪水防护措施即来源于此。此模型设置的“过流堰”截面尺寸为3 m×0.5 m见图8（a）。第二种防护措施来源于桥梁结构桥墩的防护方式——在柱（墩）前增设扰流短柱见图8（b）。短柱与房屋立柱的中心距为1 m，直径为0.4 m，高1 m。短柱可以替房屋立柱抵挡洪水冲击，改变立柱周围的流场，从而改变结构的受力特性。

3.2 计算结果分析

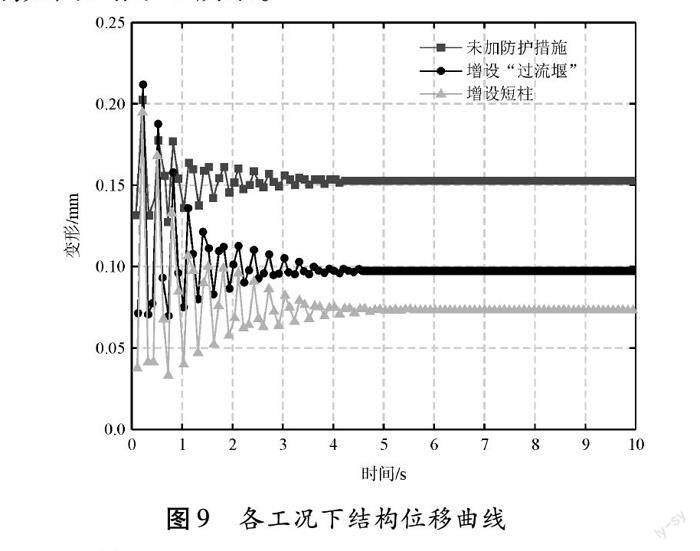
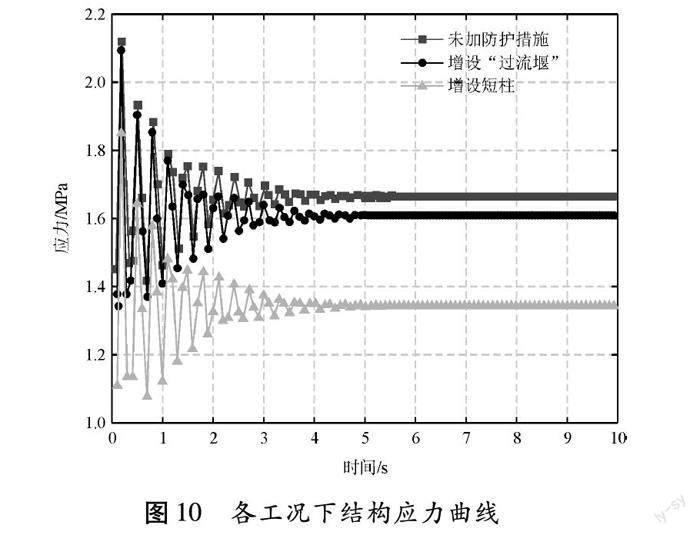
增加防护装置后的模型与前文h=4 m进行相同的边界条件设置，得出底层柱柱顶位移和上游侧中柱柱底表面应力分别如图9、图10所示。

从图9可知，结构达到稳定绕流阶段后，未增加防护措施下的位移响应值大于增设防护措施的位移响应，分别为0.134 mm、0.107 mm、0.095 mm，三者最大位移响应值接近，“过流堰”防护和短柱防护分别减小了稳定绕流阶段位移20%、29%。虽然防护装置对最大位移响应值影响不大，但其对降低稳定绕流阶段的稳定位移值具有明显效果。

从图10中可以看出，未设防护装置与过流堰防护所得柱底最大拉应力基本相同，为2.10 MPa，短柱防护所得柱底最大拉应力为1.85 MPa，较未防护情况减小13%。因瞬时冲击拉应力出现时间较短，且较混凝土极限应力强度相近，因此认为洪水来流时瞬时冲击力并不会引起结构出现致命损伤，主要以稳定绕流阶段的应力进行评估结构安全性。未加防护措施、过流堰、短柱的在稳定绕流阶段的柱底拉应力分别为1.67 MPa、1.61 MPa、1.34 MPa。根据防护装置对柱底拉应力的减弱程度，判断其防护效率，过流堰和短柱分别减小柱底拉应力4%、19%。短柱的防护能力明显高于过流堰防护，而且短柱防护使柱底承受最大拉应力低于混凝土极限抗拉强度，有效避免了混凝土开裂。

综上所述，过流堰防护对结构位移及应力响应影响较小，防护效果不明显，不能避免混凝土开裂。而增设扰流短柱能够有效减少结构位移，减小混凝土表面应力，有效避免出现拉裂缝，有很好的防护效果。

4 结束语

本文以某山区3层框架结构作为研究对象，基于流固耦合分析理论，采用数值模拟的方法，对结构在不同深度洪水冲击时的安全性，和2种防护措施进行了研究，得到结论：

（1）当水深未达到底层楼面时，随着洪水深度的增加，洪水冲击力增大，结构的位移和应力随之增加。但当洪水漫过底层楼面时，由于楼面对水流的作用，结构位移反而较小。但是结构受到的洪水冲击力和应力响应会急剧加大，威胁结构安全。因此可以适当增加首层层高，提高结构的抗洪能力。

（2）当水深未达到底层楼面时，洪水对房屋柱体的冲击压力沿高度方向呈倒“C”型分布，而且水深对压力分布的最大值和最小值影响不大。当洪水漫过楼面时，柱体在水面附近受到的压力较大，柱体其他位置的压力较小，分布较均匀。

（3）“过流堰”防护措施（门前低矮斜坡）可以显著降低结构稳定绕流阶段的稳定位移，但应力降低不明显。短柱扰流防护措施能够有效减少结构位移及柱底拉應力，降低混凝土开裂风险。且短柱扰流防护造价低，施工简单，不需作专项设计，可在山区低层房屋抗洪设计中做适当推广。

本文主要关注不同洪水深度对房屋结构的作用。其他参数，如洪水流速、含沙量等也可能影响结构的响应，这些值得后续做进一步的研究。

参考文献

［1］中华人民共和国水利部.中国水旱灾害防御公报2020［R］.2021

［2］潘佳佳，曹志先，王协康，等.暴雨山洪水动力学模型及其简化模型的比较研究［J］.四川大学学报（工程科学版），2012，44（S1）：77-82.

［3］肖诗云，王晓庆.洪水演进模型及冲击荷载数值分析［J］.工程力学，2010，27（9）：35-40.

［4］ Kundzewicz，Kanae，Seneviratne，et al. Flood risk and climate change： global and regional perspectives［J］. Hydrological Sciences Journal，2014，59（1）.

［5］ Alessio Radice，Laura Longoni，Monica Papini，et al. Generation of a Design Flood-Event Scenario for a Mountain River with Intense Sediment Transport［J］. Water，2016，8（12）.

［6］肖诗云，杨留娟，岳斌，等.不同开洞率乡村建筑洪水水流荷载试验［J］.沈阳建筑大学学报（自然科学版），2010，26（6）：1039-1045.

［7］于文，葛学礼，朱立新，等.山区乡村房屋模型水流作用试验［J］.北京交通大学学报，2011，35（1）：24-27.

［8］肖诗云，杨留娟，岳斌，等.山区乡村房屋模型洪水冲击试验研究［J］.防灾减灾工程学报，2010，30（3）：235-240.

［9］郑涵午，黄尔，路信，等.山区洪水对下游房屋冲击特性的试验研究［J］.中国农村水利水电，2020（7）：41-45.

［10］杨留娟. 山区乡村建筑洪水作用荷载试验研究［D］.大连：大连理工大学，2010.

［11］杨哲豪，吴钢锋，张科锋，等.溃坝洪水对构筑物冲击荷载的数值模拟［J］.长江科学院院报，2020，37（3）：45-50.

［12］范力阳，朱纯，杨冰清，等.移动式防洪墙系统的三维有限元模拟［J］.水科学与工程技术，2021（1）：1-3.

［13］王友彪，姚昌荣，刘赛智，等.泥石流对桥墩冲击力的试验研究［J］.岩土力学，2019，40（2）：616-623.

［14］刘杰.溃坝洪水对并联双桥墩冲击过程数值模拟［J］.人民珠江，2016，37（8）：6-9.

［15］张吉保.洪水漂浮物冲击作用下桥梁结构动力响应研究［D］.哈尔滨：哈尔滨工业大学，2016.

［16］向琪芪，李亚东，魏凯，等.桥梁基础冲刷研究综述［J］.西南交通大学学报，2019，54（2）：235-248.

［17］郭良，丁留谦，孙东亚，等.中国山洪灾害防御关键技术［J］.水利学报，2018，49（9）：1123-1136.