远程民机变弯度机翼后缘外形变形矩阵气动设计

李春鹏，钱战森，孙侠生

1.中国航空工业空气动力研究院 高速高雷诺数气动力航空科技重点实验室，沈阳 110034 2.中国航空研究院，北京 100012

远程民机具有巡航速度高、使用航程大、携带燃油多等特点，燃油消耗产生的重量变化导致巡航过程大多以非设计状态飞行，机翼翼面流场极易出现激波，由此导致阻力激增，不但降低了飞行效率，而且还因临近抖振边界而影响飞行安全。当前，通过不断增加飞行高度的阶梯巡航方式在一定程度上能够减小巡航升力变化幅度，但随着航空市场的快速发展，未来因空域紧张而增加的对飞行高度限制将会使上述问题更加突出。考虑基于固定外形机翼多点综合优化设计仅仅是性能折中的一种手段，为有效提升机翼在整个巡航阶段的综合气动性能，研究者逐渐将重点集中于后缘外形随飞行条件变化而不断调整的变弯度机翼。应用变弯度机翼技术不仅能够通过后缘变形来调整机翼载荷分布实现巡航效率提升、抖振边界扩展，还能进行阵风减缓控制，并改善机动性能，进而减小机翼结构重量、降低燃油消耗并节省成本，对未来“绿色航空”发展具有重要的促进作用。

通过后缘外形变形来改善非设计点气动性能的民机变弯度机翼技术，最早由美国国家航空航天局（National Aeronautics Space and Administration，NASA）德莱顿（Dryden）飞行研究中心于20世纪70年代提出，针对L-1011三星客机（L-1011 TriStar）研究结果表明，变弯度机翼技术名义巡航飞行状态可获得1% ～ 3%的减阻收益［1-2］。波音公司和空客公司从20世纪80年代开始评估变弯度机翼概念，并结合B777-200ER、A330/A340等开展了应用研究［3-4］，目前基于后缘刚性舵面的变弯度机翼技术已在最新的远程民机B787和A350等机型上获得了应用［5］。国内针对后缘刚性舵面的变弯度机翼技术也开展了大量的研究［6-9］。

与基于后缘刚性舵面偏转的变弯度机翼相比，基于柔性结构/变形机构的机翼后缘连续变弯度技术具有更大的变形空间、更强的翼面载荷调节能力，以及更小的飞行阻力。国内外学者围绕连续变弯后缘的气动收益问题开展了广泛的研究。Lyu等［10］采用高精度伴随求解器，针对CRM机翼开展了连续变弯后缘的气动设计研究，完成了407个飞行状态点后缘变形外形优化，系统分析了后缘连续变弯在设计点和非设计点的减阻收益及其对燃油消耗的影响。Burdette等［11］采用高精度求解器，针对uCRM模型开展了旨在减阻减重的后缘连续变弯优化设计研究，明确了后缘连续变弯节省燃油消耗的2种控制机制。Chen等［12］采用低精度气动结构分析方法，针对波音公司在亚音速超级绿色飞机研究（Subsonic Ultra Green Aircraft Research，SUGAR）项目中提出桁架支撑机翼布局，并结合连续变弯后缘襟翼开展了减阻减重优化设计研究。Ting等［13］以NASA 通用运输机标模（Generic Transport Model，GTM）模型，采用耦合跨声速小扰动方程和边界层修正的涡格法，针对多个典型飞行状态开展了连续变弯后缘襟翼减阻优化设计研究。Bui［14］利用基于RANS（Reynolds Averaged Navier-Stokes）方程的计算流体力学（Computational Fluid Dynamics，CFD）求解器，针对“湾流”III公务机机翼开展了自适应后缘（Adaptive Compliant Trailing Edge，ACTE）激波边界层干扰诱导分离控制研究。Bartels等［15］采用降阶模型从主动气弹控制角度针对桁架支撑机翼布局开展了连续变弯后缘襟翼应用研究。郭同彪［16］、聂瑞［17］、梁海朝［18］等针对跨声速翼型研究了后缘连续变弯减阻收益及影响机理。王一凡等［19］针对自然层流翼型研究了考虑整个巡航段气动性能的后缘连续变弯优化设计方法。李春鹏等［20］针对带有连续变弯后缘跨声速翼型开展了考虑后缘自适应变形的基本翼型多点优化设计研究。王斌等［21］针对宽体客机变弯度机翼开展了后缘连续变弯气动优化设计研究，对比分析了后缘变弯与前后缘同时变弯的气动差异。郭同彪等［22］针对民机机翼-机身-平尾构型开展了考虑配平约束的后缘连续变弯度机翼气动优化设计研究。雷锐午等［23］基于典型民机标模开展了考虑抖振性能约束的机翼后缘变弯减阻优化设计研究。

结合二维翼型和三维机翼开展的相关研究已充分验证了连续变弯后缘在改善整个巡航阶段气动性能的技术优势，但在工程应用中，连续变弯后缘气动外形设计还应考虑变形结构变形能力、飞行控制系统操纵逻辑等因素对弦向和展向变形外形的约束。本文以远程民机标模为研究对象，基于机翼后缘指关节变形结构，从保证后缘随升力单调偏转角度，开展连续变弯后缘外形变形矩阵气动优化设计研究。首先结合机翼某展向站位翼型剖面完成连续变弯后缘的弦向变形方式筛选，然后针对全机构型，对比分析了后缘协调变形对变弯度机翼气动收益的影响规律，从多点关联和阶梯变形角度构建了巡航任务剖面变形矩阵，并进一步研究了抖振抑制和阻力发散点减阻等非巡航任务剖面下的变形矩阵设计方法。

1 研究模型

基于远程民机标模基本气动外形，参考机翼后缘原有常规舵面，在80%翼展范围内布置弦向和展向均与机翼光滑连接的柔性变弯后缘，设定7个变弯控制剖面以保证后缘具有足够的变形能力，典型变弯度机翼后缘变形外形与基本外形对比见图1。

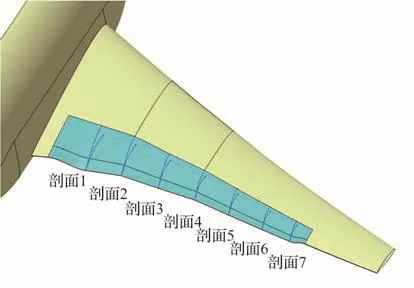
图1 变弯度机翼后缘变形外形对比Fig.1 Comparison of variable camber wing trailing edge shape

指关节变形结构作为一种典型变弯后缘结构形式，由能相互独立偏转的分段刚性组成，分段之间通过柔性蒙皮光滑连接，具有结构简单、刚度强度大、承载能力强等突出优势［24］。参考3段式指关节变形结构，保留其末段具有一定弦向占比且外形不可变的特征，忽略其内段结构对后缘外形的限制，定义变弯控制剖面外形曲线（图2）：根据变弯后缘剖面上下翼面确定基本外形中弧线，将中弧线按一定比例分为3段，考虑结构变形能力限制，确定末段中弧线占比25%，且保留与之相对应的上下翼面基本外形。结合3段中弧线的前端点确定后缘变弯外形控制转轴，各段中弧线除绕其前端转轴偏转外，还随其前端中弧线的转动而转动。将旋转前的上下翼面基本外形前端与旋转后的末段中弧线对应上下翼面基本外形前端利用二次样条曲线光顺连接形成变形后的变弯控制剖面。

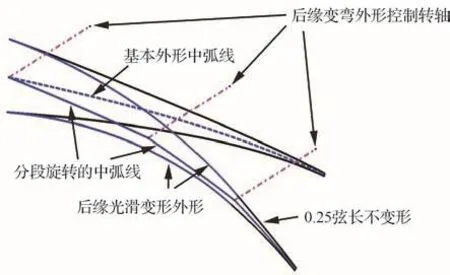
图2 变弯控制剖面几何外形定义Fig.2 Geometric shape definition of deformation shape control section

变弯度机翼后缘外形变形在调整机翼翼面载荷分布的同时也会产生一定的俯仰力矩增量，为了计及配平俯仰力矩带来的阻力影响，需在开展气动特性评估之前，确定与变弯度机翼后缘变形外形的相对应的全动平尾配平偏度，全动平尾及其转轴见图3。

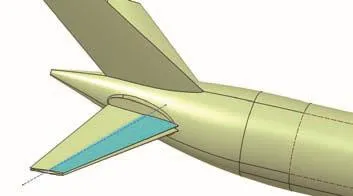
图3 全动平尾及其转轴Fig.3 All-movable horizontal tail and its rotation axis

2 计算方法及验证

2.1 计算方法

数值模拟采用三维N-S方程，在直角坐标系中三维N-S方程守恒形式可表示为

式中：w为状态矢量；f为无黏（对流）通矢量项；fv为黏性（耗散）通矢量项。

采用Menter’s SST湍流模型，利用有限体积法控制方程离散，通过多重网格加速收敛。为提高计算效率，采用半模计算。远场与计算域中心距离为20倍机身长度，网格为多块结构化网格，在飞行器表面附近生成棱柱层网格以捕捉边界层内的流动特征，第1层网格高度为飞机参考长度的10-6，壁面网格法向增长率1.25，棱柱层数33层，半模网格点数800万左右。物面采用无滑移条件，对称面采用对称边界条件，远场由当地一维黎曼不变量确定。

2.2 计算验证

选择第5届阻力预测会议跨声速民机标模CRM翼身组合体构型来验证方法的可靠性。采用结构网格计算，网格点为800万左右，马赫数Ma= 0.85，雷诺数Re= 5.0×106，升力系数CL= 0.486。计算模型及网格见图4。

图4 CRM翼身组合体模型及计算网格Fig.4 CRM wing-body model and computational mesh

4个展向站位机翼剖面压力分布与试验［24］对比如图5所示［25］，图中：2yb为当地展向站位距对称面距离与半展长的比值。计算得到的不同站位翼面压力系数分布形态、前缘吸力峰、激波强度等关键流场特征与试验基本一致，仅靠近翼梢站位剖面的激波位置略有偏差，说明本文所采用的方法具有较高精度，可用于远程民机变弯度机翼的气动分析和优化研究。

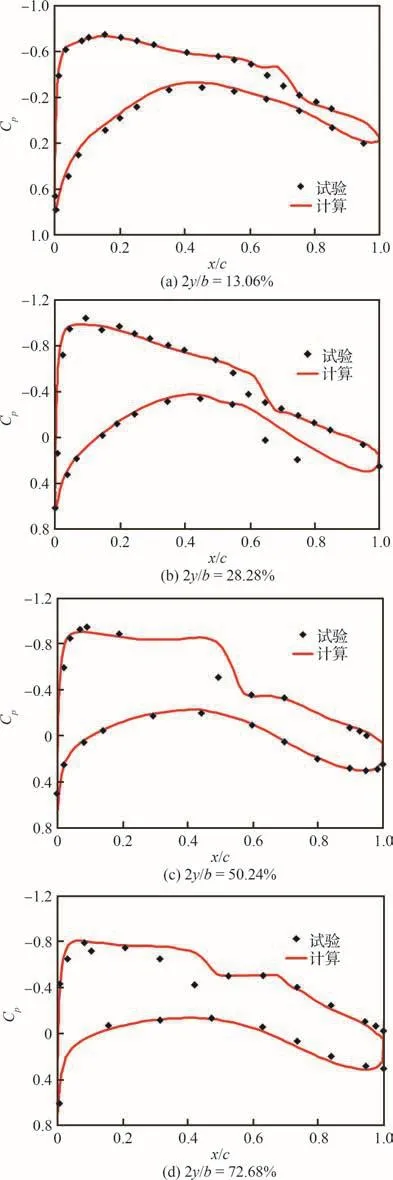
图5 CRM翼身组合体计算与试验翼面压力系数对比［25］Fig.5 Pressure coefficient comparison of computational result and test data of CRM wing body［25］

3 基于代理模型的优化方法

根据几何外形成型方式确定变弯度机翼后缘外形优化设计变量，利用通用优化平台参数化建模、网格自动化生成和高精度流场计算等模块实现设计变量对应响应值的自动求解，选取代理优化算法完成给定状态的设计变量寻优，结合后缘外形间变形关联关系制定气动优化策略，进而完成变弯度机翼后缘外形变形矩阵气动优化流程搭建。

3.1 代理优化算法

代理优化算法是在基于试验设计构建初始代理模型的基础上，按照一定的优化加点准则（如MSP、EI、PI、MSE、LCB等），采用传统优化算法求解相应的子优化问题，以较小计算代价实现最优解的高效预测，并将预测最优解及其真实响应值添加到用于构建代理模型的数据集，通过代理模型不断更新来实现新增样本序列向最优解收敛［26］，代理优化算法典型框架如图6所示。

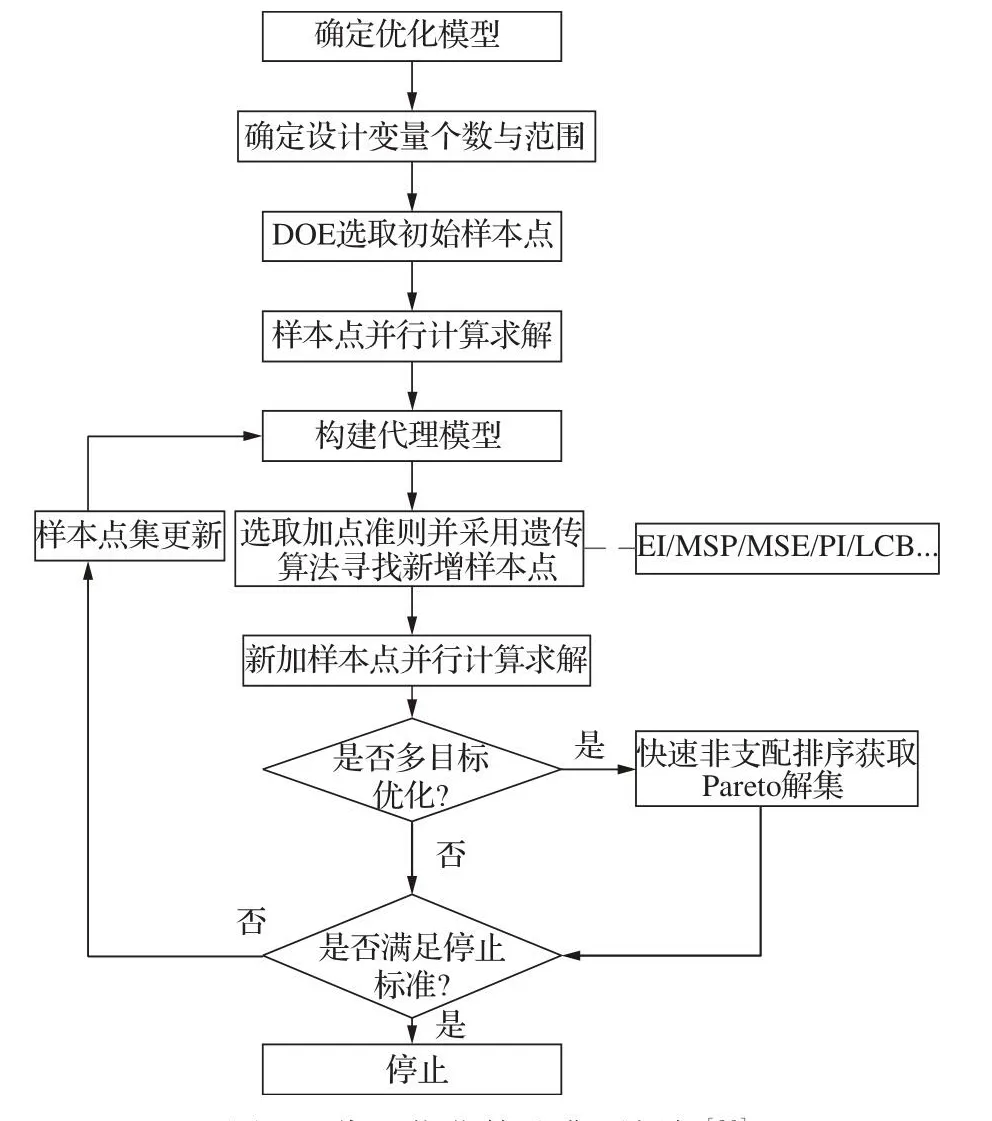
图6 代理优化算法典型框架［26］Fig.6 Framework of surrogate-based optimization algorithm［26］

代理优化算法既可借助代理模型替换复杂、费时的高精度数值计算，又可基于历史数据求解优化加点准则定义的子优化问题，在提高优化效率和改善全局搜索能力等方面均具有明显的优势。

本文选用拉丁超立方方法进行试验设计，代理模型为Kriging模型，利用EI、MSP等加点准则完成优化过程中的代理模型更新，采用遗传算法与序列二次规划相结合的方法对优化加点准则定义的子优化问题寻优［27］。

3.2 气动优化策略

区别于几何形状固定的机翼单目标优化或多目标优化问题，变弯度机翼后缘外形变形矩阵的气动优化设计可理解为一种具有耦合关系的单目标优化设计问题，尽管变形矩阵内单个设计点对应的后缘外形气动优化是单目标问题，但受变形关联关系约束，其外形优化设计空间选取与变形矩阵内其他设计点的后缘外形相关。在满足后缘外形变形结构约束的前提下，为了充分挖掘变弯度机翼后缘变形的气动收益，针对具有耦合关系的单目标优化问题制定的气动优化策略为

1） 根据远程民机变弯度机翼后缘外形变形需求确定设计状态矩阵。

2） 确定矩阵内关键设计状态，根据优先程度完成全部设计状态的分层。

3） 根据设计状态分层关系逐步调整后缘外形优化设计变量的取值范围，并以此为基础完成后缘外形变形矩阵的气动优化。

4） 综合对比变形矩阵内的后缘外形，根据气动收益及变形关联关系调整后缘变形外形。

此外，为提高气动优化效率，以后缘基本外形阻力系数为基准，只在具有减阻收益时进行配平计算，否则将其阻力系数叠加某一特定值（明显大于阻力系数的大量，如99）做坏点处理。

变弯度机翼后缘外形变形矩阵气动优化流程见图7，其中设计状态矩阵主要是以升力系数阶梯变化为特征的巡航任务剖面和以抖振、阻力发散为特征的非巡航任务剖面两种情况确定，结合后缘外形变形需求，按变形程度筛选矩阵内关键设计状态，按优先程度完成设计状态分层，优化设计变量的取值范围随着优先层级的降低而逐渐收缩。对后缘变形外形完成几何参数化建模，确定设计变量及其取值范围，按最大的设计变量空间完成高层级设计状态对应的试验设计，获取代理模型构建所需的初始样本点集，通过自动化模型和网格生成、数值计算完成样本对应的气动性能参数求解。利用初始样本点集完成代理模型构建后，结合代理模型加点准则定义代理子优化问题并完成代理模型参数寻优，将得出的待加点作为更新样本在获取其气动性能精确解后加入样本点集并完成代理模型更新，以更新样本的气动性能提升程度作为收敛条件，如果相邻迭代样本的气动性能差量小于规定值即完成优化，输出由更新样本组成的后缘变形外形气动优化解集，解集选取范围为规定值范围内最优气动性能对应的样本。结合高层级设计状态优化结果，按层级关系依次确定其他设计状态对应的设计变量取值范围，并完成后缘变形外形气动优化解集求解。最后围绕设计状态矩阵，兼顾气动收益和变形关联关系，从保证各设计状态后缘外形曲线相似的角度，对后缘变形控制剖面偏度调整，进而确定变弯度机翼后缘外形变形矩阵。

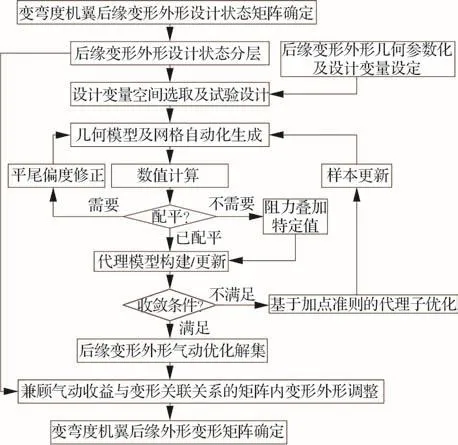
图7 后缘外形变形矩阵气动优化设计流程Fig.7 Aerodynamic optimization design process of trailing edge deformation matrix

4 后缘变弯控制剖面变形方式影响

参考3段式指关节变形结构确定的变弯控制剖面最多需要4个变量来描述，包括1个中弧线比例分段变量和3个分段中弧线旋转角度变量。选取不同控制变量组合的后缘外形变形能力对比见图8，其中4个变量的顺序分别为中弧线比例分段变量、前段中弧线旋转角度变量、中段中弧线旋转角度变量和后段中弧线旋转角度变量，单变量是3段中弧线共用的旋转角度变量，而将中弧线比例分段变量固定为0.45。相对采用单变量取值为5描述的变弯控制剖面变形外形，采用4变量组合描述的变弯控制剖面变形外形在后缘点接近的情况下具有更大范围的后缘变形控制能力。

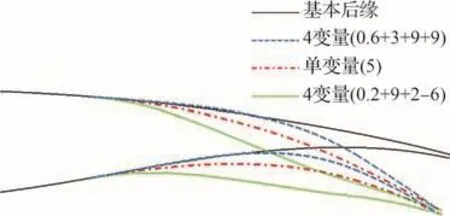
图8 后缘外形变形方案变形控制能力对比Fig.8 Deformation control capability comparison of different trailing edge schemes

选取某远程民机标模机翼典型展向站位翼型剖面，结合不同升力系数的二维流场后缘外形变形方式的影响。按照后掠翼理论确定二维翼型设计马赫数Ma= 0.7、雷诺数Re= 1.0×107，设计升力系数CL及设计变量取值范围如表1所示。

二维翼型后缘变形外形气动优化设计结果对比如图9所示，优化方案对应二维翼型后缘外形设计变量取值如表2所示，典型升力系数下后缘外形对比如图10所示，可以看出单变量及4变量变形方式虽然变形能力不同，但两者获得的气动收益相当。相对升力系数CL= 0.7对应的翼型设计点，升力系数偏离越远，后缘变形幅度越大，所获得的气动收益也越大。对于小升力系数对应的后缘上偏状态，2种变形方式获得的几何外形略有差异，而对于大升力系数对应的后缘上偏状态，两种变形方式获得的几何外形基本一致。

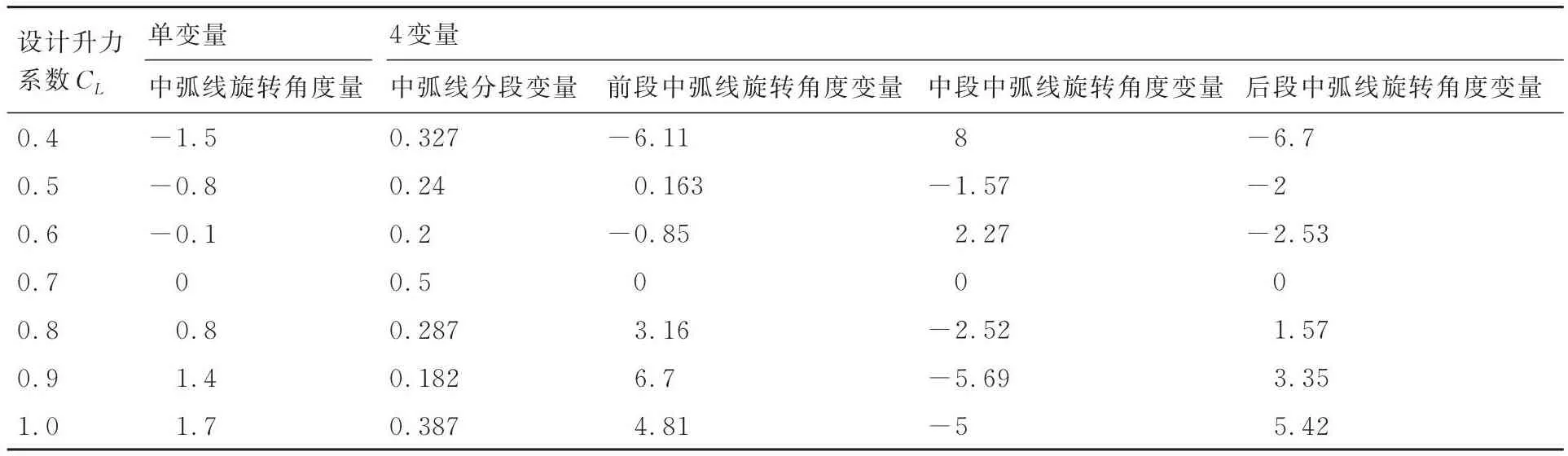
表2 二维翼型后缘外形优化设计结果Table 2 Aerodynamic optimization results of 2D airfoil trailing edge deformation shapes

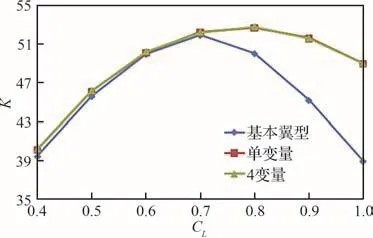
图9 二维翼型后缘变形外形升阻比曲线Fig.9 Lift-to-drag ratio curves of different airfoil trailing edge deformation shape

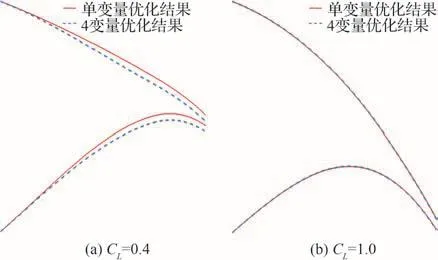
图10 二维翼型后缘优化外形对比Fig.10 Aerodynamic optimization geometric comparison of 2D airfoil trailing edge deformation shapes

以上分析表明，对于3段中弧线旋转角度相同的单变量控制方式，尽管变形能力相对有限，但外形变形规律更符合升力大幅变化情况下的流场控制需求，更适用于变弯度机翼后缘变形外形的气动优化设计研究。

5 巡航任务剖面变形矩阵

对于飞行马赫数和高度固定的巡航任务剖面，远程民机在定常平飞过程中的升力系数会随着燃油消耗而逐渐减小，巡航任务剖面起始点燃油最多，对应升力系数最大，巡航任务剖面终止点燃油最少，对应升力系数最小。

某远程民机标模巡航马赫数Ma= 0.85，巡航高度H= 11 km，以升力系数CL= 0.48对应的半油状态作为基准确定巡航任务剖面中点，按20%的燃油变化量确定巡航任务剖面起始及终止点，按10%的燃油变化量确定巡航任务剖面前段及后段中点，得出变弯度机翼后缘变形外形巡航任务剖面设计状态矩阵见表3。

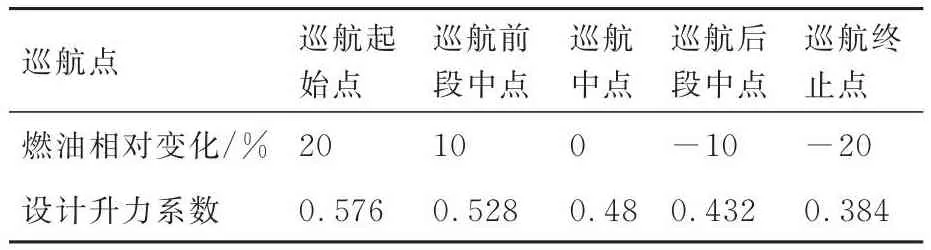
表3 巡航任务剖面设计状态矩阵Table 3 Aerodynamic design matrix of cruise flight profile

5.1 单点最优变形矩阵

为明确变弯度机翼后缘外形变形在不同升力系数下的最大减阻空间，分别针对巡航任务剖面中不同燃油变化对应的设计升力系数，选取相同的设计变量空间，开展变弯度机翼后缘变形外形气动优化设计，形成单点最优变形矩阵。

变弯度机翼后缘外形的变弯控制剖面采用单变量控制方式描述，共计7个设计变量，每个变量的取值范围均为-5 ～ 5，非配平及配平状态下的优化结果气动特性对比见表4，表中：ΔCD为后缘变形外形相对基本外形的减阻量，α为飞行迎角，δtail为平尾偏度。从优化结果可知，非配平及配平状态下的变弯度机翼后缘外形变形减阻规律基本一致，且考虑配平约束后的减阻收益略大。相对升力系数CL= 0.48对应的半油基准状态，减阻收益随着升力系数变化量的增加而增大，但主要的减阻收益集中在升力系数增加的高升力状态，对于同等幅度的升力系数变化量，高升力系数时后缘外形变形所能获得的减阻量约为低升力系数时的7 ～ 8倍。

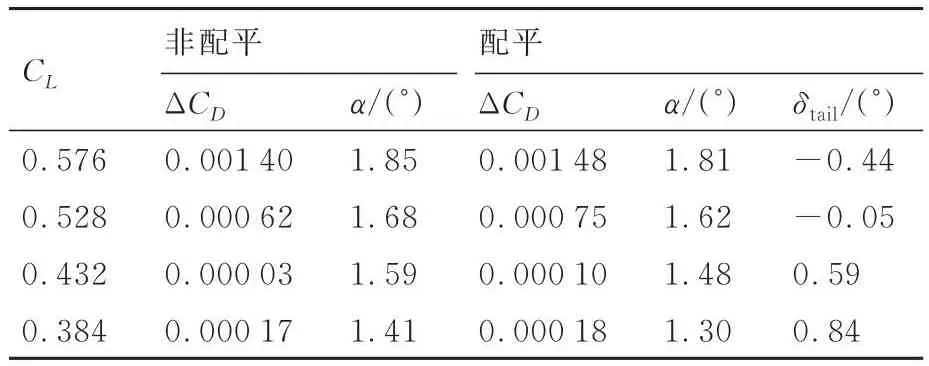
表4 单点最优变形矩阵优化结果气动特性对比（Ma =0.85，H = 11 km）Table 4 Aerodynamic characteristics comparison of single-point optimal deformation matrix optimization results（Ma = 0.85，H = 11 km）

单点最优变形矩阵后缘外形变弯控制剖面偏度对比见图11，图中：正值代表相应变弯控制剖面下偏，负值代表相应控制剖面上偏，下同。非配平及配平状态下的变弯控制剖面偏转规律基本一致，随着设计升力系数的增加，内侧5个变弯控制剖面逐渐下偏，而外侧2个变弯控制剖面则先上偏后下偏。对于非配平状态，内侧5个变弯控制剖面在固定升力系数下的偏度相差较小，外侧2个变弯控制剖面的偏度在低升力系数时与内侧相差不大，但在高升力系数状态，特别是相对基准升力增加20%时的偏度相对内侧明显增大。对于配平状态，以中间变弯控制剖面4为分界点，后缘外形变弯控制剖面偏度在固定升力系数下整体呈先减小后增加的趋势，这种展向偏度变化也减小了外侧变弯控制剖面在高升力系数时的绝对偏度。整体来看，对于完全不考虑后缘外形变形关联关系所获得的变形矩阵，在巡航飞行过程中，随着燃油的不断消耗，不同后缘外形变弯控制剖面在偏转控制方面没有明显的规律性，主要表现为各剖面偏度增量的差别较大，在个别状态还存在反向偏转，后缘变形控制逻辑较为复杂，难以满足实际工程应用要求。

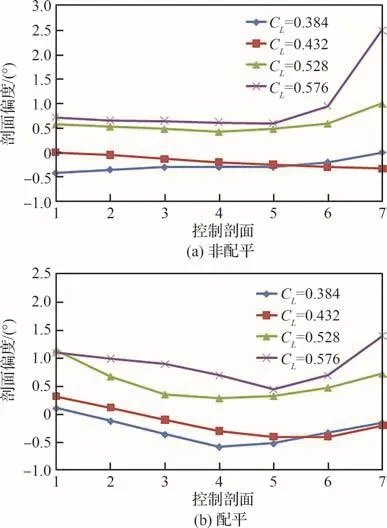
图11 单点最优变形矩阵后缘外形变弯控制剖面偏度对比（Ma = 0.85，H = 11 km）Fig.11 Deflection angles comparison of trailing edge deformation shape control sections in singlepoint optimal deformation matrix（Ma = 0.85，H = 11 km）

5.2 多点关联变形矩阵

基于配平状态下的单点最优变形矩阵气动优化设计结果，考虑后缘外形变形关联关系，开展变弯度机翼后缘变形外形气动优化设计，形成多点关联变形矩阵。

构建多点关联变形矩阵的关键在不同升力系数对应后缘变形外形气动优化设计变量空间的选取。考虑到后缘外形变形在小升力系数下的减阻能力有限，额外增加设计约束难以获得足够的减阻收益，因此以巡航任务剖面最小设计升力系数状态对应的后缘变形外形为约束依次设定设计变量的取值范围。

针对巡航任务剖面设计状态矩阵，配平条件下的多点关联变形矩阵气动优化按2种思路展开（图12）：①按单点最优变形矩阵确定设计变量最大值，并将其作为不同设计点共用的设计空间上边界，以邻近较小升力系数设计点对应的设计变量取值为设计空间下边界，按照设计升力系数从小到大的顺序完成多点关联变形矩阵的气动优化设计，优化过程中下边界逐渐缩小；②结合单点最优变形矩阵中最大及最小升力系数设计点确定设计空间的初始上下边界，按照设计升力系数从两端到中间的顺序依次完成多点关联变形矩阵的气动优化设计，优化过程中上下边界同时缩小。

图12 多点关联变形矩阵气动优化设计思路Fig.12 Aerodynamic optimization design ideas of multi-point coupling deformation matrix

按照2种设计变量空间选取思路获得的配平状态多点关联变形矩阵气动优化设计结果气动特性对比见表5，表中：ΔCD为后缘变形外形相对基本外形的减阻量，ΔDCD为后缘变形外形相对单点最优变形外形的增阻量。相比于单点最优变形矩阵，下边界逐渐缩小方式获得的变形矩阵最大阻力系数增量仅为0.000 05，上下边界同时缩小方式获得的变形矩阵最大阻力系数增量仅为0.000 01。综合优化算法寻优能力等因素限制，可认为考虑后缘外形变形关联关系的设计变量空间缩减并不会产生明显的减阻收益损失。

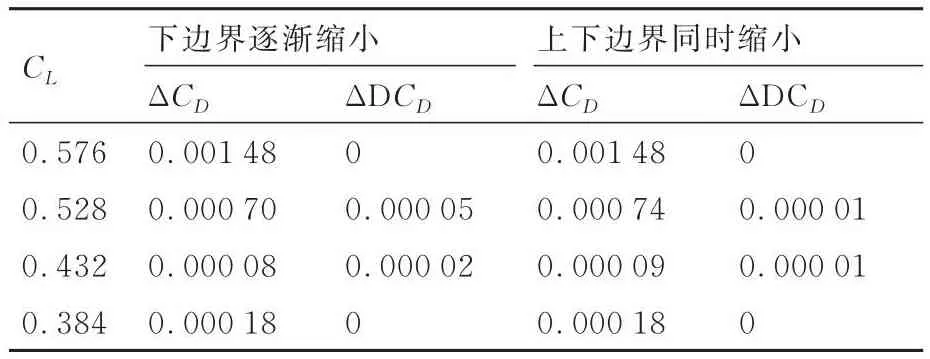
表5 配平状态多点关联变形矩阵优化结果气动特性对比（Ma = 0.85，H = 11 km）Table 5 Aerodynamic characteristics comparison of multi-point coupling deformation matrix optimization results under trimmed condition（Ma = 0.85，H = 11 km）

配平状态多点关联变形矩阵后缘外形变弯控制剖面偏度对比如图13所示。尽管设计变量空间选取方式不同，会形成差别较大的后缘外形变形矩阵，但相比于单点最优变形矩阵，多点关联变形矩阵内不同设计点对应的后缘变弯控制剖面偏度具有明显规律性，即随着巡航过程中升力系数的减小，不同展向站位的后缘变弯控制剖面只需同向等比例的偏转即可近似获取最优变形外形。

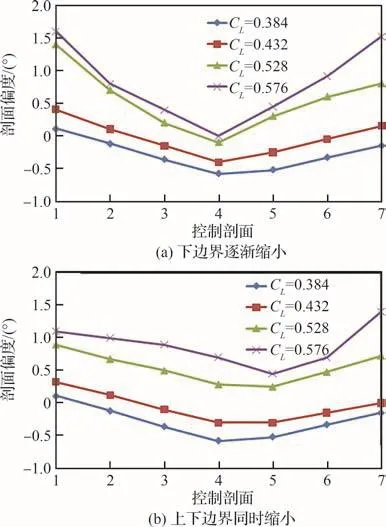
图13 配平状态多点关联变形矩阵后缘外形变弯控制剖面偏度对比（Ma = 0.85，H = 11 km）Fig.13 Deflection angles comparison of trailing edge deformation shape control sections in multipoint coupling deformation matrix under trimmed condition（Ma = 0.85，H = 11 km）

巡航任务剖面最小和最大升力系数设计状态对应多点关联变形矩阵后缘外形与后缘无偏转的基本外形在配平状态下的内、中、外3个展向站位翼面压力分布对比如图14和图15所示，其中内侧展向站位对应后缘外形变弯控制剖面1，中间展向站位对应变弯控制剖面4，外侧展向站位对应变弯控制剖面6。

图14 后缘外形变形对翼面压力分布影响（Ma = 0.85，H = 11 km，CL = 0.384配平状态）Fig.14 Effect of trailing edge deformation on pressure coefficient distribution（Ma = 0.85，H = 11 km，CL = 0.384 trimmed condition）

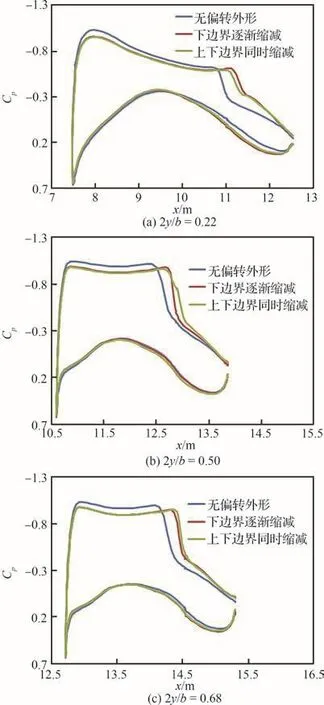
图15 后缘外形变形对翼面压力分布影响（Ma = 0.85，H = 11 km，CL = 0.576的配平状态）Fig.15 Effect of trailing edge deformation on pressure coefficient distribution（Ma = 0.85，H = 11 km，CL = 0.576 trimmed condition）

在小升力系数设计状态（CL= 0.384），只有一种后缘变形外形方案，内侧展向站位后缘外形变弯控制剖面下偏0.11°，翼面压力分布没有明显变化。中间展向站位上偏0.58°，外侧展向站位上偏0.15°，变弯控制剖面上偏主要影响上翼面的压力分布变化，具体表现为前缘吸力峰后的低压区向后扩展，变弯后缘前端所处的当地负压强度降低、范围减小，翼面外侧后缘附近激波强度降低，剖面压心前移。在大升力系数设计状态（CL= 0.576），按照设计变量空间选取的差异，多点关联变形矩阵优化获得两种后缘变形外形方案，在内、中、外3个展向站位，下边界逐渐缩减方案的后缘变弯控制剖面偏度分别为下偏1.6°、不偏转（0°）和下偏0.92°，上下边界同时缩减方案的后缘变弯控制剖面偏度分别为下偏1.1°、0.7°和0.7°，尽管2种外形方案在不同展向站位的后缘变弯控制剖面偏度差别较大，其影响仅局限于变弯后缘型面附近的激波位置变化，翼型前半部分的压力变化基本一致，整体表现为负压强度降低和负压范围的向后扩展，剖面压心后移。由此可知变弯度机翼减阻的关键在于通过后缘外形变形调整主翼部分的压力分布，后缘当地型面的压力分布变化影响较小，同时也说明了对于同一升力系数确实存在多种后缘外形变形方案。

5.3 阶梯变形矩阵

结合变弯度机翼后缘外形变形巡航任务剖面减阻收益对变弯控制剖面偏度不敏感的特点，基于多点关联变形矩阵，从均衡巡航任务剖面减阻收益角度开展阶梯变形矩阵气动设计。

选定设计变量空间上下边界同时缩减的配平状态多点关联变形矩阵，综合矩阵内后缘变形外形变弯控制剖面偏转规律确定偏转基准，分别以最小和最大升力系数为边界，按巡航任务剖面内中间升力系数与边界升力系数的比例关系，确定与升力系数线性对应的阶梯变形矩阵。典型升力系数下的阶梯变形矩阵与多点关联变形矩阵对比见图16，两者整体偏度基本一致，仅在外侧展向站位略有偏差。

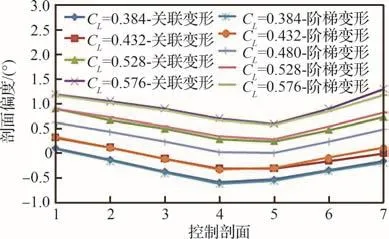
图16 阶梯变形矩阵与多点关联变形矩阵后缘外形变弯控制剖面偏度对比Fig.16 Deflection angles comparison of trailing edge deformation shape control sections between step deformation matrix and multi-point coupling deformation matrix

阶梯变形矩阵内后缘变形外形相对多点关联变形矩阵和无偏转基本后缘的气动特性对比见表6，表中ΔCD1为阶梯变形矩阵相对基本后缘的阻力系数减小量，ΔCD2为阶梯变形矩阵相对多点关联变形矩阵的阻力系数减小量。结果表明，后缘外形变形调整后的阶梯变形矩阵仍然具有理想的减阻收益，与优化得到的多点关联变形矩阵相比，阻力系数增量不超过0.000 02。

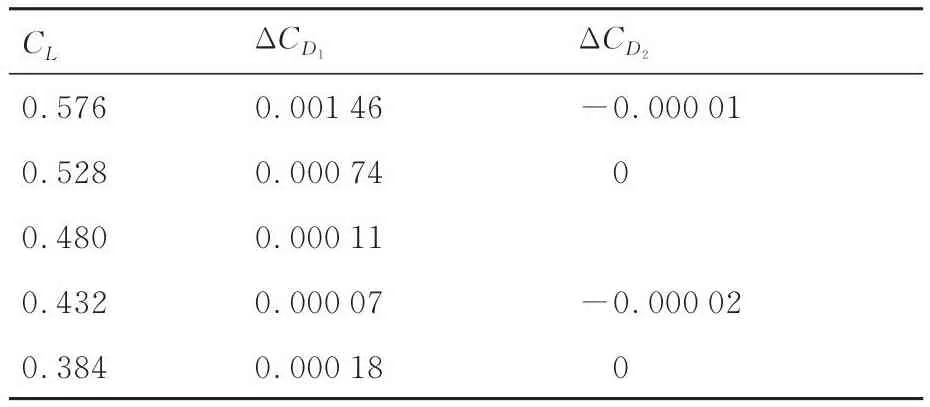
表6 配平状态阶梯变形矩阵后缘变形外形阻力系数减小量（Ma = 0.85，H = 11 km）Table 6 Drag coefficient reduction of step deformation matrix trailing edge deformation under trimmed condition（Ma = 0.85，H = 11 km）

值得注意的是，变弯度机翼后缘外形变形减阻收益随着设计升力系数的增加而增大，根据升力系数等间距划分设计状态矩阵确定后缘外形阶梯变形矩阵存在减阻收益失衡问题，即矩阵内减阻收益小的后缘变形外形过多，而减阻收益大的后缘变形外形过少。为此在大升力系数区间内针对性的加密设计点来构建新的设计状态矩阵和阶梯变形矩阵，新增设计点下阶梯变形矩阵后缘变形外形阻力系数减小量对比见表7，表中ΔCD3

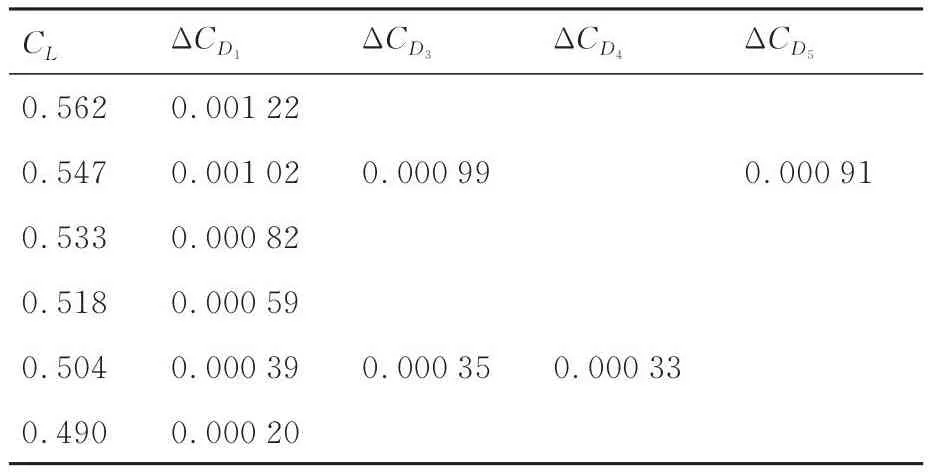
表7 配平状态新增设计点阶梯变形矩阵后缘变形外形阻力系数减小量（Ma = 0.85，H = 11 km）Table 7 New added design points drag coefficient reduction of step deformation matrix trailing edge deformation under trimmed condition（Ma = 0.85，H = 11 km）

为阶梯变形矩阵CL= 0.528对应后缘变形外形相对基本后缘的阻力系数减小量，ΔCD4为阶梯变形矩阵CL= 0.480对应后缘变形外形相对基本后缘的阻力系数减小量，ΔCD5为阶梯变形矩阵CL= 0.576对应后缘变形外形相对基本后缘的阻力系数减小量。通过数据对比可以看出，在大升力系数区间，基于阶梯变形矩阵获得的后缘变形外形减阻量与设计升力系数基本呈线性关系。在CL= 0.480 ～ 0.576的大升力系数区间，相比于加密设计状态矩阵，不增加设计点时产生的最大阻力系数增量不小于0.000 11（ΔCD1-ΔCD5，CL= 0.547），增加一个设计点（CL= 0.528）时，产生的最大阻力系数增量不小于0.000 04（ΔCD1-ΔCD3，CL= 0.504）。

6 非巡航任务剖面变形矩阵

考虑航空管制等实际应用场景和相关设计规范要求，在民机机翼精细化气动设计中，大升力系数时的抖振特性和飞行马赫数增加时的阻力发散特性等非巡航任务剖面性能也需要重点考虑。

某远程民机标模巡航马赫数Ma= 0.85，巡航高度H= 11 km，设计升力系数CL= 0.48，以此为基准，选定1.3g过载状态为抖振点（Ma=0.85，H= 11 km，CL= 0.624）开展变弯度机翼后缘外形变形抖振抑制效能分析，选定阻力发散点（Ma= 0.87，H= 11 km，CL= 0.48）开展减阻收益研究。

6.1 大升力系数下的抖振抑制变形

根据单点最优变形矩阵和多点关联变形矩阵气动优化设计方法获得抖振点的后缘变形外形方案变弯控制剖面偏度对比如图17所示。考虑后缘变形外形与CL= 0.576对应方案的相似性，将单点最优抖振抑制变形方案视为下边界逐渐缩减多点关联变形方案。可以看出，尽管2种抖振抑制方案在中内侧的变弯控制剖面偏度差异明显，但抖振抑制变形规律基本相同，都是仅在CL= 0.576对应方案的基础上上偏外侧变弯控制剖面，且增加的偏度也相差不大。

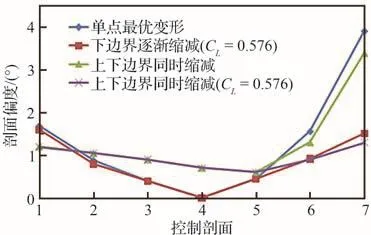
图17 配平状态抖振抑制方案后缘外形变弯控制剖面偏度对比Fig.17 Deflection angles comparison of buffeting suppression scheme trailing edge deformation shape control sections under trimmed condition

后缘外形抖振抑制变形方案相对后缘不偏转的基本外形减阻收益对比如表8所示，阻力系数减小量超过0.003 5，其中设计变量空间更大的单点最优变形方案略大。

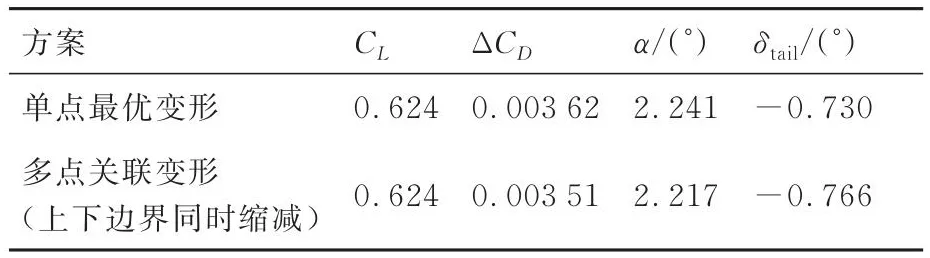
表8 配平状态抖振抑制方案后缘变形外形阻力系数减小量（Ma = 0.85，H = 11 km）Table 8 Drag coefficient reduction of buffeting suppression scheme trailing edge deformation under trimmed condition（Ma = 0.85，H = 11 km）

后缘外形抖振抑制变形方案机翼表面压力分布云图及极限流线对比如图18所示，典型变弯控制剖面翼面压力分布对比如图19所示。总体上2种后缘变形方案的流场相差不大，典型剖面的压力分布几乎完全重合，都是通过增加后缘载荷、降低机翼前段负压强度的方法来降低翼面激波强度，进而减小阻力。但受制于后缘外形变形能力限制，翼面激波强度仍较大，未能完全消除翼面后缘的流动分离。

图18 抖振点后缘外形变形对翼面流场分布影响（Ma =0.85，H = 11 km，CL = 0.624配平状态）Fig.18 Effect of buffeting point trailing edge deformation on pressure coefficient distribution（Ma = 0.85，H = 11 km，CL = 0.624 trimmed condition）

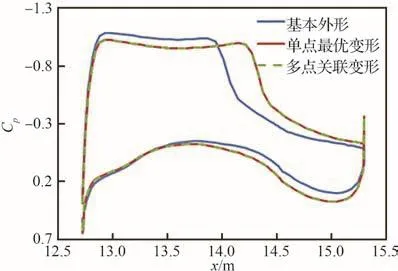
图19 抖振点后缘外形变形对2y/b = 0.68剖面压力分布影响对比（Ma = 0.85，H = 11 km，CL =0.62配平状态）Fig.19 Effect of buffeting point trailing edge deformation on pressure coefficient distribution at 2y/b=0.68（Ma = 0.85，H = 11 km，CL =0.624 trimmed condition）

6.2 阻力发散马赫数下的减阻变形

根据单点最优变形矩阵设计方法获得非配平及配平条件下的阻力发散点减阻后缘变形方案变弯控制剖面偏度对比如图20所示。在不考虑配平要求时，后缘变形外形呈内侧上偏、外侧下偏的特点，在配平条件下，相对于Ma= 0.85的巡航状态，后缘变形外形同样呈内侧上偏、外侧下偏的规律，但内侧偏度略小。

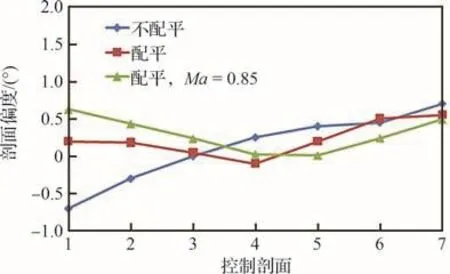
图20 阻力发散减阻方案后缘外形变弯控制剖面偏度对比Fig.20 Deflection angles comparison of drag divergence scheme trailing edge deformation shape control sections

阻力发散点后缘变形减阻收益对比如表9所示，非配平状态下的后缘变形相比后缘不变形的基本外形阻力系数减小0.000 25，配平状态下的阻力系数减小量仅为0.000 11，减阻收益降低超过50%。

非配平及配平状态下的阻力发散点减阻后缘变形方案与基本外形在典型变弯控制剖面的翼面压力分布对比分别如图21和图22所示。此时内侧及外侧变弯控制剖面上偏及下偏仅能够影响后缘附近的激波位置，但对剖面前段的压力几乎没有影响，由此也进一步表明后缘外形变形无法有效控制主要由激波阻力决定的阻力发散。

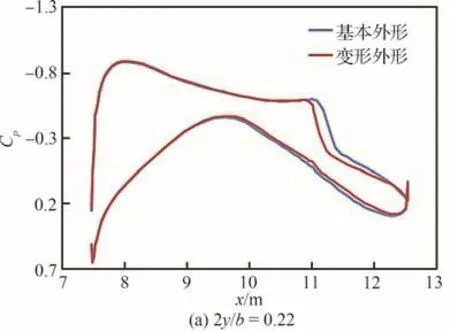
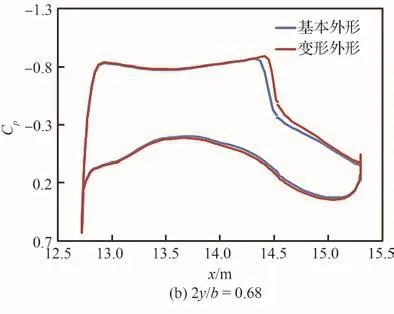
图21 阻力发散点后缘外形变形对翼面压力分布影响（Ma = 0.87，H = 11 km，CL = 0.48非配平状态）Fig.21 Effect of drag divergence point trailing edge deformation on pressure coefficient distribution（Ma = 0.87，H = 11 km，CL = 0.48 untrimmed condition）

7 结论

选取基于代理模型的优化方法，以某远程民机标模为研究对象，在选定变弯控制剖面参数化方法的基础上，开展了考虑变形关联约束的变弯度机翼后缘外形变形矩阵气动设计研究。针对某远程民机标模，得出结论如下：

1） 对于参考指关节变形结构确定的后缘外形变弯控制剖面，采用三段中弧线旋转角度相同的单变量控制方式尽管变形能力有限，但是完全能够满足变弯度机翼后缘变形外形的气动优化设计要求。

2） 对于飞行马赫数和高度固定、仅升力系数随燃油消耗而逐渐减小的巡航任务剖面，变弯度机翼后缘外形变形的减阻收益随着升力系数相对基准状态变化量的增加而增大，且高升力状态减阻量约为同等变化幅度对应低升力状态的7 ～ 8倍。

3） 在小升力系数状态，后缘外形变形能够扩展前缘吸力峰后的低压区，减小变弯后缘当地的负压强度，压心前移；在大升力系数状态，后缘外形变形能够降低主翼负压强度并向后扩展负压范围，压心后移。

4） 变弯度机翼减阻的关键在于通过后缘外形变形调整主翼压力分布，但对变弯控制剖面的偏度不敏感，后缘外形变形关联关系约束不会明显减小后缘外形变形的减阻收益。

5） 存在后缘外形变弯控制剖面偏转规律相同、偏度与升力系数线性对应，且减阻收益明显的巡航任务剖面阶梯变形矩阵，相比基于升力等间距变化的阶梯划分，基于减阻量等间距变化的阶梯划分能够在整个任务剖面内获得更大的减阻收益。

6） 大升力区间内的巡航任务剖面阶梯变形矩阵，后缘外形变弯控制剖面偏度、后缘变形外形对应设计升力系数、后缘外形变形减阻量3者之间均呈线性关系。

7） 对于由抖振点和阻力发散点确定的非巡航任务剖面变形矩阵，变弯度机翼后缘外形变形相对巡航任务剖面变形矩阵同样具有明显的规律性，抖振点的后缘外形变形能够通过改变翼面载荷分布和激波强度而减小阻力，但不能完全翼面消除分离。阻力发散点的后缘外形变形对主翼部分压力分布影响较小，无法有效控制主要由激波阻力决定的阻力发散。