基于PSO-BiLSTM神经网络的机身筒段应力预测
2023-06-28杨超张开富
杨超,张开富
1.西北工业大学 机电学院,西安 710072
2.中国航空工业集团公司北京长城航空测控技术研究所,北京 101111
飞机机身筒段是构建飞机气动外形的重要组成部分,具有尺寸大、形状复杂、容易变形等特点,筒段中的蒙皮和长桁等零件都属于易变形薄壁零件。飞机制造过程中,前机身、中机身和后机身通常是在不同的地方分别制造,最后运输到一起进行机身对接装配。运输过程中,柔性薄壁机身筒段会在重力的作用下发生形变,机身部件的制造误差、定位误差和温度变化以及零件刚度弱等因素的存在导致实际机身部件与理论模型有较大差距,过大的初始误差增大了机身装配的难度。因此在筒段装配对接前,需要形状控制工装对飞机筒段进行形状调整[1]。目前机身筒段形状控制工艺受工人经验差异的影响,导致机身形状因人而异、质量稳定性差、返修率高和控形耗时长,因此迫切需要设计出自动化可调工装进行弱刚性大部件的形状控制。为避免自动化可调工装控形过程中局部应力过大造成筒段损坏,控形过程中需要时刻关注筒段圆桁表面实时应力数据和应力变化趋势,常规的应用有限元计算应力的时间代价较大,不能满足控形过程中的应力监测实时性要求。应用电阻应变片传感器可以对飞机筒段圆桁表面应力进行精确地监测,但只能对之前的时刻进行监测,不能对未来数据趋势进行分析预测,因此如何快速准确地预测控形过程中筒段圆桁表面的应力显得尤为重要,预测的效率和精度进而决定了控形过程应力优化的效率和准确性。
薄壁机身筒段在装配前受制造、运输、重力等因素影响,筒段呈现出不规则形状,导致筒段在控形过程中,筒段圆桁的应力变化具有非线性变化特点,使用传统方法难以计算出筒段准确应力。考虑到机身薄壁筒段控形过程应力具有时序相关性,采用一种基于双向长短期记忆神经网络的深度学习模型进行机身薄壁筒段控形过程中的应力预测,并搭建机身筒段试验台验证应力预测方法的有效性。LSTM神经网络是一种改进的循环神经网络,由于LSTM神经网络的激活函数是sigmoid函数与tanh函数相结合,所以避免了竞争模型循环神经网络(Recurrent Neural Network, RNN)反向传播求导时会出现梯度消失和梯度爆炸的情况,大大加快了模型收敛速度。
国内外学者在应力预测和LSTM神经网络方面做了一些研究。唐成顺[2]、袁泓磊[3]、Gulgec[4]等基于LSTM神经网络分别建立了汽轮机转子表面应力预测模型,甘蔗转运车关节点应力预测模型,钢制结构的振动、应力预测模型,并通过多次实验验证,验证了应力预测模型的高效性和稳定性。Huang等[5]基于LSTM神经网络模型预测油井性能,与传统储层数值模型相比,LSTM神经网络模型在计算速度和精度方面有明显的优势。Ma等[6]提出一种基于LSTM神经网络和混合优化算法的自适应修改方法,用于补偿涡轮风扇发动机在健康状态下的实验数据和非线性分量级模型之间的初始误差。Hajiaghayi和Vahedi[7]使用LSTM神经网络模型进行代码故障预测和模式提取,并利用贝叶斯优化算法优化网络模型超参数,实验表明,该方法优于决策树和随机森林等经典学习模型。标准LSTM神经网络在学习长序列信息时,记忆细胞长度通常不能满足需求,会出现梯度消失问题,BiLSTM神经网络很好的解决了这个问题,国内外学者将BiLSTM神经网络应用在多个领域。Zhang[8]基于BiLSTM神经网络建立了航空发动机转子多故障特征参数预测参数模型;Pan等[9]基于BiLSTM神经网络检测卫星遥测异常数据;车畅畅等[10]通过BiLSTM神经网络预测性能退化趋势;Bian等[11]基于BiLSTM神经网络捕获前向和反向电池时间信息。通过上述学者在BiLSTM神经网络领域的研究实验结果可以看出,基于BiLSTM神经网络的预测模型在长序列信息记忆能力上有显著提升。一些学者为了增强LSTM神经网络的学习能力和预测能力,提出改进型LSTM神经网络,并应用在各个领域。Liu等[12]采用LSTM-RNN模型预测燃料电池的剩余寿命;Que等[13]提出一种改进自编码长短期记忆 (Auto-Encoder-Long Short-Term Memory Neural Networks, AE-LSTM) 神经网络,用来预测飞机飞行过程中的异常数据;Li等[14]提出了卷积神经网络和长短期记忆 (Convolutional Neural Network-Long Short-Term Memory,CNN-LSTM) 神经网络混合网络应力预测模型,预测橡胶拉伸变形过程中应激数据;Sun等[15]提出基于长短时记忆神经网络和高斯过程回归(Long Short-Term Memory Neural Networks-Gaussian Process Regression, LSTM-GPR)混合模型,可在不降低LSTM神经网络模型预测精度的情况下,准确预测船舶运动姿态。Yao等[16]提出一种基于深度学习的模糊粗糙集和长短期记忆 (Fuzzy Rough Set-Long Short-Term Memory, FRS-LSTM) 神经网络模型,采用模糊粗糙理论进行短期风速预测,实验表明,预测精度高于传统神经网络。Du等[17]建立基于RNN和LSTM神经网络的车辆速度预测模型,经实验结果表明,在预测数据较长的情况下,LSTM神经网络预测误差更小,具有更好的性能。Ma等[18]使用纵向BiLSTM神经网络建立刀具磨损预测模型,根据刀具切削力预测的磨损值误差在8%以内。
对于本文需要计算的机身薄壁筒段应力,应用有限元计算的时间成本较高,应用传统多层前馈神经网络无法处理应力预测的时序序列问题,而RNN在处理时序序列问题时也因为序列数据过长而导致不易克服的梯度消失和梯度爆炸问题。因此为快速准确的计算和预测机身薄壁筒段应力,建立了基于BiLSTM神经网络的机身筒段应力预测模型,并使用粒子群算法优化BiLSTM神经网络超参数,提高预测模型训练效率和选取更优的参数组合降低预测误差。为验证提出的解决方法的有效性,使用RNN和标准LSTM神经网络进行对比试验分析。
1 相关理论及方法
1.1 BiLSTM神经网络
RNN和LSTM神经网络都是依据之前时刻的时序信息来预测下一时刻的信息,不能结合未来时刻的信息,但是在一些问题中,当前时刻的信息输出不仅与之前的状态有关,还与未来的状态有关,此时就需要将之前的时序信息和未来的时序信息都输入到神经网络中,本文提出双向长短期记忆神经网络用于飞机薄壁圆筒控形过程中更精准的应力预测。Cui[19]和Siami-Namini[20]等对LSTM神经网络和BiLSTM神经网络进行过详细的比较,结果表明BiLSTM神经网络在相应的时间系列任务中优于LSTM神经网络。
BiLSTM神经网络与标准LSTM神经网络结构相同,BiLSTM神经网络也是由基本的细胞状态、输入门、遗忘门和输出门组成,BiLSTM神经网络的基本原理是由一个向前的标准LSTM神经网络和一个向后的标准LSTM神经网络组成,标准LSTM神经网络基本结构如图1所示。
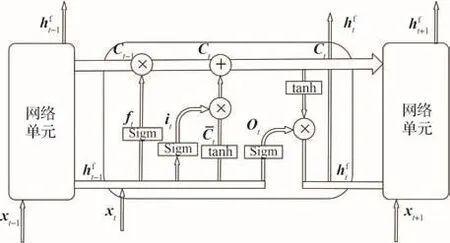
图1 标准LSTM神经网络结构Fig.1 Standard LSTM neural network structure
BiLSTM神经网络结构由双向循环神经网络和标准LSTM神经网络组成,BiLSTM神经网络包含2个训练方向的LSTM神经网络,每层的网络节点都包含完整的过去信息与未来信息,2个训练方向最后都与输出层相连。BiLSTM神经网络结构如图2所示。
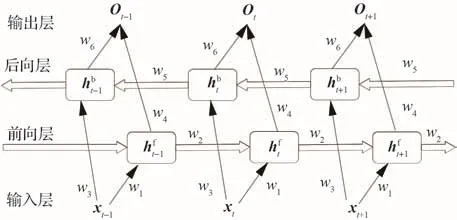
图2 BiLSTM神经网络结构Fig.2 BiLSTM neural network structure
1.2 粒子群算法
粒子群优化(Particle Swarm Optimization,PSO)算法是一种基于动物种群觅食的随机优化技术,受鸟群和鱼群觅食过程中的生物行为和群集行为的启发,Kennedy和Eberhart[21]于1995年提出粒子群算法。将觅食中的每只鸟都看作空间中搜索的粒子,有自己的速度和位置特征。粒子在空间中的运动会结合自身判断和群体共享信息,分别称为局部搜索和全局搜索,粒子会结合全局搜索最佳位置和局部搜索最佳位置决定运动方式并指向目的地,并且会更新局部搜索最佳位置然后将其保存下来,最终实现从局部最优到全局最优的搜索过程。
2 预测模型构建
BiLSTM神经网络模型训练过程中需要调节很多超参数,只有输入和输出参数可以直接确定,输入是一个应力检测点的历史检测数据,因此BiLSTM神经网络模型的输入层单元个数与输入数据维度都是相同的,输出维度与全连接层单元个数相同。其他参数包括隐藏层神经元数量、学习率、训练迭代次数和滑窗大小都对机身筒段应力预测非常重要,但是无法直接计算出。若通过正交试验法获得最优组合超参数,将耗费大量的资源和时间,并且不能确保得到的超参数组合是最优解。因此本文使用粒子群算法优化双向长短期记忆神经网络超参数,提出基于PSO-BiLSTM神经网络的机身筒段应力预测模型。
Greff等[22]的实验表明对LSTM神经网络模型影响最大的超参数是学习率,其次是最大迭代次数和隐藏层神经元数量,网络深度对LSTM神经网络模型的准确度影响最小,因此本文采用单层BiLSTM神经网络模型。将学习率lr、最大时代ep、隐藏层神经元数量lb、辍学率dp这4个主要超参数和滑动窗口大小、培训批次大小、学习率下降因子这3个次要超参数作为PSO算法的对象,基于PSO-BiLSTM神经网络的机身筒段应力预测模型流程图如图3所示。具体步骤为

图3 基于PSO-BiLSTM神经网络的机身筒段应力预测模型流程图Fig.3 Flow chart of stress prediction model of fuselage tube section based on PSO-BiLSTM neural network
步骤 1采集机身筒段控形过程中应力数据,构建应力预测数据集。
步骤 2对应力数据进行归一化处理,采用离差标准化方法对应力数据进行线性变换,映射到[0,1]范围内,提高应力预测精度和加快模型梯度下降求最优解的速度。
步骤 3将归一化后的数据分为训练集Train_x、Train_y和测试集Test_x、Test_y,再分别划分为输入数据和数据标签。
步骤 4初始化粒子群,并以各粒子对应参数构建BiLSTM神经网络模型,通过训练数据进行模型训练,将预测结果的均方根误差(Root Mean Square Error, RMSE)作为各粒子的适应度值。
步骤 5将适应度值作为终止条件,若满足终止条件,返回最优超参数取值,否则,返回步骤 4。
步骤 6粒子群优化算法根据BiLSTM神经网络模型适应度更新粒子并确定粒子全局最优位置,构建PSO-BiLSTM神经网络应力预测模型。
步骤 7将测试集输入数据放入训练好的预测模型中,将输出数据与测试集测试结果Test_out进行比较,根据均方根误差计算应力预测模型误差。
为了客观评价预测结果的准确性和有效性,选用RMSE、平均绝对误差(Mean Absolute Error, MAE)和决定系数R2评估不同应力预测模型的准确性,其表达式分别为
式中:yi为应力真实值为应力预测值为应力真实值的平均值;m为应力预测次数。
应力预测模型基于python,实验使用的计算机环境为:windows10,E-2286M处理器,12 G内存,Tesla T4显卡(12 G显存),tensrflow2.0。
3 实验验证及结果分析
3.1 搭建实验台
为了测试预测模型的可行性和有效性,使用飞机机身筒段进行控形应力预测实验。以某型号客机为原型,制造1∶4缩比模型,模型包括机身筒段主体和形状控制工装,如图4和图5所示。

图4 某型客机机身筒段主体1∶4缩比模型Fig.4 A 1∶4 scaled model of main body of fuselage tube section for a certain type of passenger aircraft
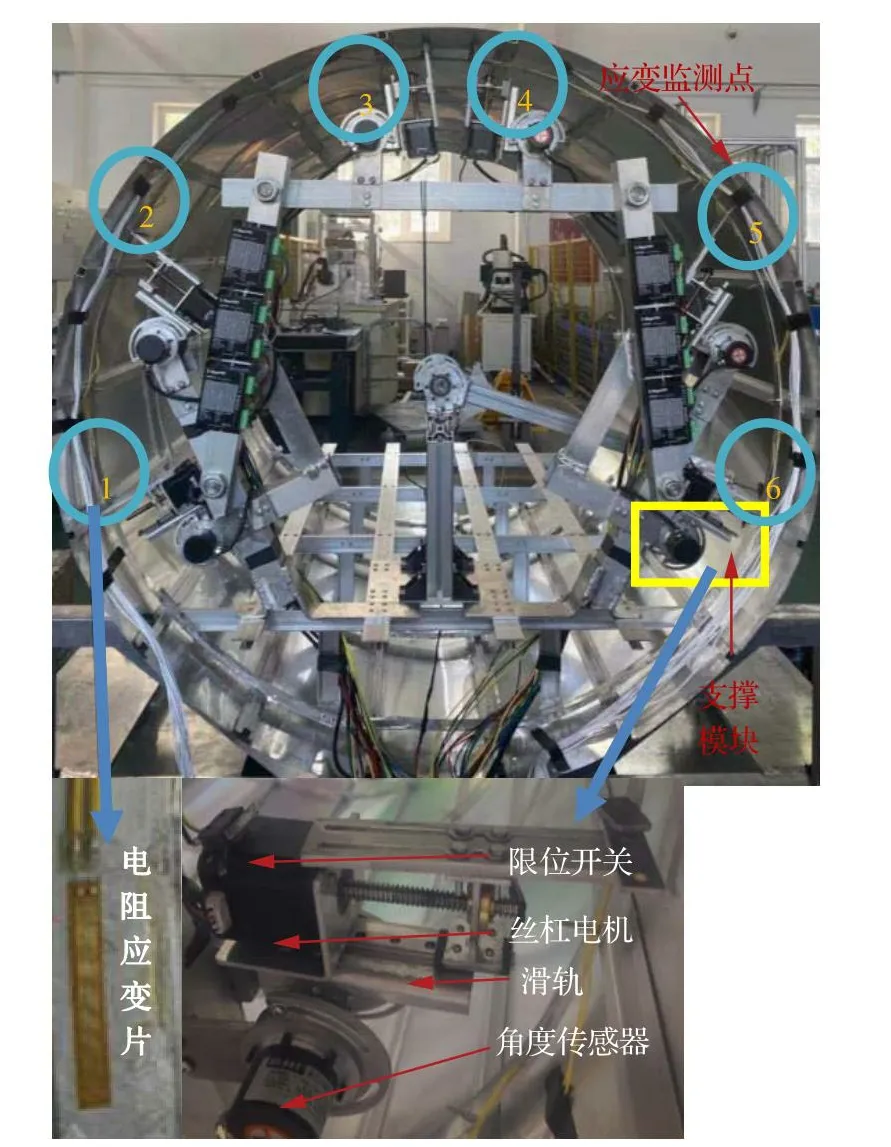
图5 形状控制工装Fig.5 Tooling for shape control
机身筒段由桁架和蒙皮组成,因为蒙皮厚度仅0.5 mm,所以蒙皮和圆桁受重力影响会发生一定的形变,筒段还会受到制造误差和运输振动的影响,导致机身筒段在装配前可能出现不规则的变形,例如局部塌陷或左右不对称。
为了克服筒段出现的不规则变形,在筒段对接一侧安装形状控制工装调节筒段形状,如图5所示,形状控制工装由框架和6个支撑模块组成,支撑模块对称安装在框架上,可径向支撑圆桁达到控制筒段形状的目的。圆桁上贴有6个电阻应变片,如图蓝色圆圈位置,用来监测控形过程中筒段应力变化,筒段中心设有可旋转的位移检测传感器。旋转1周采集12个预设标记点位置,通过拟合计算出筒段变形位置及变形量。
3.2 采集控形应力数据
在室内温度27 ℃的条件下,进行机身筒段形状控制应力采集实验,以0.5 mm/s的速度驱动步进电机移动,控制机身筒段形状,以0.1 s为采样间隔,采集电阻应变片数据和机身筒段形状变化量。为了增强PSO-BiLSTM神经网络应力预测模型的鲁棒性,采集不同初始状态下筒段控形的应力数据,对重力状态下静置的机身筒段进行人工干预,改变机身筒段形状,模拟机身筒段受不可控因素出现不规则形状的情况,然后采集不同变形情况下机身筒段形状控制的应变变化数据。针对筒段上6个应力监测点,对其进行应变采集实验,通过在筒段长桁上添加重物的形式对机身筒段做出8次形状改变,以模拟机身筒段在重力和运输振动影响下的不规则变形。然后分别采集8组应变变化数据,将其中7组作为训练数据,1组作为测试数据进行应变预测实验。图6所示为6个应变监测点在8次形状调整实验中的应变监测数据。
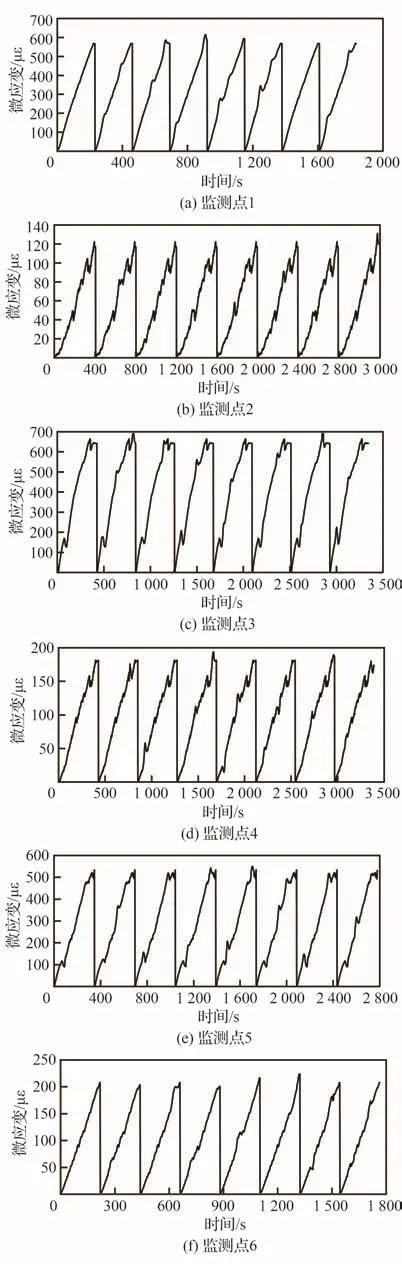
图6 机身筒段监测点应变监测数据Fig.6 Strain monitoring data at monitoring point of fuselage tube section
上述实验数据中,出现应力下降和跌宕起伏的原因是机身筒段控形过程中,6个支撑点一起运动,且支撑速度和支撑距离并非线性的,1个监测点的应力可能受其他5个支撑点变化的影响。应用6个应力监测点数据集分别训练6个应力预测模型,因为6个应力监测点应变变化相似,所以本文选择应变变化较为复杂的监测点2和监测点4,用于展示模型训练过程和预测准确度。监测点2和监测点4分别有3 200和3 400个历史数据作为训练数据,为了实现连续预测和克服样本数据少而带来的深度学习模型训练不准确问题,采用滑动窗口处理方法处理样本训练数据,通过滑动窗口方法不但可以重复利用样本训练数据,提高控形过程中应力相邻元素的相关性,还可以增加应力预测模型训练的样本数量,在应力预测过程中具有更强的鲁棒性。因此,飞机机身应力预测问题变成一个回归问题。滑动窗口处理方法会将样本数据重构为BiLSTM神经网络模型需要的三维输入格式,更加适应时间序列模型的输入。
3.3 应力预测结果及分析
以数据集中前7组数据作为训练数据,最后1组数据作为测试数据,分别对4种应力预测模型进行训练和测试。RNN、标准LSTM神经网络和BiLSTM神经网络在模型训练过程中均需要手动调节模型超参数,确定最佳参数的方法是在保持其他参数不变的情况下,仅调整相关参数以获得最佳预测性能。而PSO-BiLSTM神经网络可以利用粒子群优化算法自动优化模型超参数,需要调节的超参数包括:学习率(0.001~0.1)、隐藏层神经元数量(30~200)、最大时代(50~500)、辍学率(0.2~0.5)、优化器(Adam)和学习率下降因子(0~0.6)。优化后的4个应力预测模型最佳超参数见表1和表2。
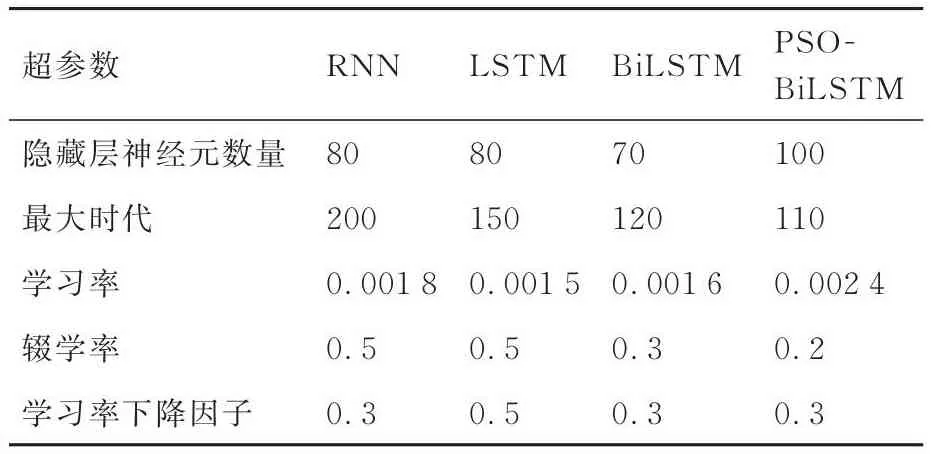
表1 4种应力预测模型超参数(监测点2)Table 1 Four kinds of stress prediction model hyperparameters at monitoring point 2
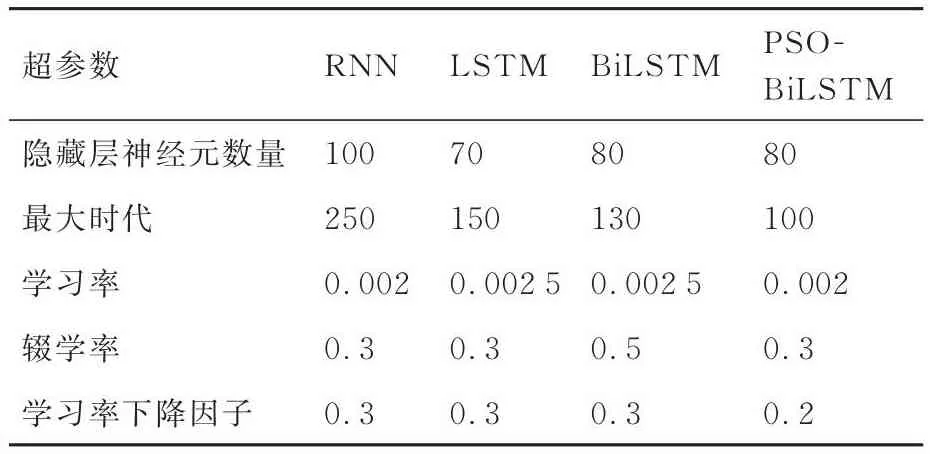
表2 4种应力预测模型超参数(监测点4)Table 2 Four kinds of stress prediction model hyperparameters at monitoring point 4
为了研究PSO-BiLSTM神经网络模型在模型训练阶段的高效率和稳定性,将BiLSTM神经网络模型和PSO-BiLSTM神经网络模型训练时的损失函数曲线进行分析对比,图7和图8分别为BiLSTM神经网络模型和PSO-BiLSTM神经网络模型训练过程中的RMSE误差收敛曲线。
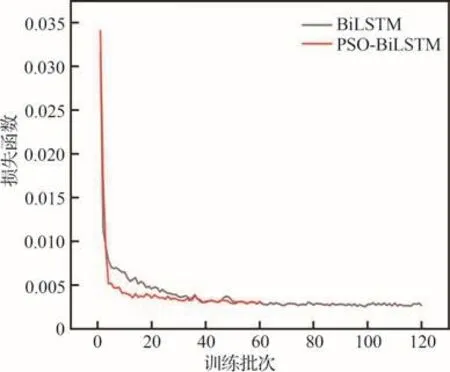
图7 监测点2模型训练RMSE误差收敛曲线Fig.7 Model training RMSE error convergence curve at monitoring point 2

图8 监测点4模型训练RMSE误差收敛曲线Fig.8 Model training RMSE error convergence curve at monitoring point 4
由以上2个监测点的模型训练误差收敛时间可以看出,BiLSTM训练50个时代后基本稳定,在120个时代后训练停止,而PSO-BiLSTM只需要20个时代就基本达到稳定值,在80个时代后训练停止,加入粒子群优化算法后训练效率提升了50%,且在PSO-BiLSTM神经网络中加入了提前退出迭代的算法,通过设置适应度函数变化容忍度,每次迭代完成后计算与上一次迭代的适应度函数之差,连续8次达到阈值即退出迭代,极大的节省了超参数调优工作量。并且PSOBiLSTM神经网络模型的RMSE误差比BiLSTM神经网络模型的RMSE误差更小,在监测点1的训练过程中RMSE误差达到0.0032,这表明粒子群优化算法可以在模型训练迭代过程中获得更优的参数来优化BiLSTM模型。结果表明,PSO-BiLSTM神经网络模型的训练效率更高且超参数调优能力更好。
为了验证4种应力预测模型的实际预测效果,分别测试数据集第8组数据,PSO-BiLSTM神经网络模型的超参数完全由粒子群优化算法得出最优解,其他3个模型的超参数为表1中最优组合解。应变预测性能分析如图9和图10所示。
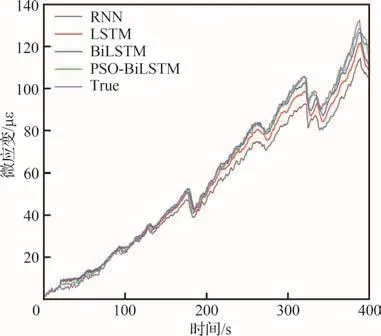
图9 监测点2应变预测性能分析Fig.9 Strain prediction performance analysis at monitoring point 2

图10 监测点4应变预测性能分析Fig.10 Strain prediction performance analysis at monitoring point 4
在以上2个监测点的应力预测实验中,4个应力预测模型均可以实现对应力变化趋势的基本预测。应力预测性能比较:PSO-BiLSTM>BiLSTM>LSTM>RNN。RNN模型预测的数据曲线与真实曲线有较大偏差,在应力数据变化大的部分不能准确预测,例如监测点1中300~350 s的预测偏差达到了18,这是因为RNN模型没有长期记忆细胞,当新的隐藏层数据输入就会覆盖原有数据信息,造成梯度爆炸损失预测,在长序列数据预测方面具有不可弥补的缺陷。标准LSTM神经网络在RNN的基础上增加了1路输入和1路输出,通过新增的长期记忆细胞可以保留更多的序列数据,预测准确度相比RNN模型有较大提升,但是标准LSTM神经网络模型在面对应力变化较大的预测问题时,仍然存在明显的预测结果滞后问题,这是因为序列式数据存在自相关性。标准LSTM神经网络模型需要以序列式数据作为输入,滑动窗口的应用让输入数据中当前时刻的值与其自身上一时刻的值具有一阶自相关性,此缺陷不可避免,且滞后性导致的误差会随着时间的推移越来越大。多数情况下,BiLSTM神经网络模型的预测结果与真实结果偏差较小,在正向预测和反向预测的叠加处理后,梯度消失问题和预测滞后问题都得到解决。在应力预测的前半部分,BiLSTM神经网络模型和PSO-BiLSTM神经网络模型的预测准确度都很高,与真实曲线基本拟合,随着时间的推移,BiLSTM神经网络模型的预测准确度略低于PSO-BiLSTM神经网络模型,这是因为人为调节BiLSTM神经网络模型超参数不能使模型发挥出最佳性能,经过粒子群优化算法调优的PSO-BiLSTM神经网络模型不仅训练速度快,在预测稳定性方面也有明显提高。
为进一步验证PSO-BiLSTM神经网络模型的预测性能,表3和表4给出了4种预测模型在2个应力监测点的评价指标计算结果。PSOBiLSTM神经网络模型的RMSE、MAE都低于其他预测模型,在决定系数R2评价标准中,该模型计算结果比其他预测模型更接近1,表明其预测性能优于其他模型。监测点2的评价指标计算结果中,PSO-BiLSTM神经网络模型的RMSE比RNN模型低66%,比LSTM神经网络模型低56.6%,比BiLSTM神经网络模型低20%,其模型预测精度显著提高,在PSO-BiLSTM神经网络模型与BiLSTM神经网络模型具有相同单元结构的情况下,PSO-BiLSTM神经网络模型依靠粒子群优化算法优秀的超参数寻优能力显著提高了预测精度。
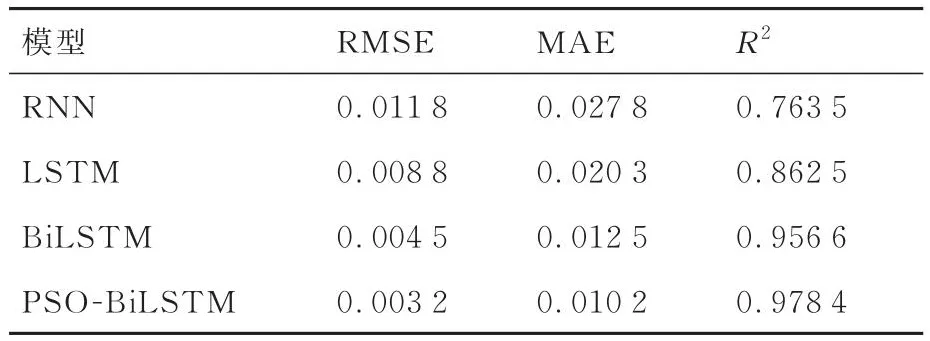
表3 4种模型评价指标比较(监测点2)Table 3 Comparison of evaluation indicators of four kinds of model at monitoring point 2

表4 4种模型评价指标比较(监测点4)Table 4 Comparison of evaluation indicators of four kinds of model at monitoring point 4
4 结 论
1)使用滑动窗口提取应力数据相关信息,可以提高序列式数据相关性,使预测结果更加稳定。
2)应用RNN、LSTM神经网络和BiLSTM神经网络分别对数据集进行训练和测试,实验结果表明,BiLSTM神经网络对于相关性强的长序列信息预测性能最好,可以较好地解决梯度消失问题和预测结果滞后问题。
3)将PSO算法与BiLSTM神经网络相结合,使用PSO算法对BiLSTM神经网络超参数进行迭代优化,解决了人为调参的不确定性并提高了工作效率,实验结果表明,基于PSOBiLSTM神经网络的应力预测模型可在飞机薄壁筒段控形过程中提供准确且快速的应力预测结果。
