基于RBF神经网络的3-UPS/S稳定平台运动学标定

田文杰，赵 堃，张熙临，王丽娜，张相鹏

基于RBF神经网络的3-US/S稳定平台运动学标定

田文杰1，赵 堃1，张熙临2，王丽娜2，张相鹏1

(1. 天津大学海洋科学与技术学院，天津 300072；2. 天津大学机械工程学院，天津 300350)

三自由度并联构型稳定平台常用作船载稳定平台对船舶扰动进行补偿，姿态精度是并联构型姿态稳定平台的重要性能指标，由于机构中各项几何与非几何误差源之间具有强耦合、非线性等特点，难以建立包含全部误差源的误差模型用于运动学标定．针对该问题，本文提出了一种基于等效误差模型以及RBF神经网络的关节空间误差补偿方法，该方法首先基于伪误差理论将因几何、非几何误差引起的机构动平台姿态误差等效视为仅由驱动关节杆长误差所引起，进而采用RBF神经网络建立了名义驱动关节变量与驱动关节杆长伪误差之间的非线性映射模型．此后，为提升网络泛化性能与动平台姿态误差预测精度，针对性地设计了一种二级分层网络训练方法，下层构建网络线性结构，上层采用粒子群优化(PSO)算法同步全局优化网络扩展常数与正则化参数．最后，采用PSO-RBF在3-US/S并联姿态稳定平台上开展了关节空间等效误差预测仿真和作业空间误差补偿实验研究，结果表明，本文所提方法具有高度的灵活性和适用性，可高精度刻画名义驱动变量与驱动关节杆长伪误差之间的映射关系，且网络输出变量可直接用于运动学标定，关节空间中的杆长精度提升了93.6%，作业空间中的姿态精度提升了92.3%，有效提升了标定效率与精度，验证了所提方法的正确性和有效性．

姿态稳定平台；运动学标定；伪误差模型；RBF神经网络；PSO算法

海上船舶由于受风、浪、流等海洋环境扰动的影响，会产生6个自由度的波动．对于搭载科学探测仪器进行海洋观测任务的海洋观测船舶来说，横摇、纵摇、艏摇3个自由度运动带来的姿态角变动，会严重影响探测仪器的测量精度．采用三转动自由度机构作为船载姿态稳定平台实时补偿船体的姿态变动，是有效的工程解决方案之一．

由于并联机器人在有效载荷、刚度、精度、响应速度等方面的优势[1]，非常适用于在船舶等局促空间内搭载仪器设备，并对其动态变化的姿态角进行补偿．船载稳定平台能否有效补偿船舶运动对船载设备的影响，一方面在于对稳定平台的稳定控制，但对于高精度补偿，稳定平台自身的精度也是影响补偿效果的重要因素．因此，对稳定平台进行机构误差分析，并进行相应的误差补偿对提高稳定平台的运动精度及姿态补偿效果具有重要意义．

影响并联机器人精度的误差来源主要包括几何参数误差和非几何参数误差[2-3]．几何参数误差往往能够通过基于误差模型的传统运动学标定方法来标定，标定过程包括误差建模、误差测量、参数辨识、误差补偿．许多学者利用该方法针对不同机构进行了大量的研究工作[4-6]．虽然传统运动学标定方法具有收敛速度快以及误差源清晰的优点，但是往往需要建立复杂的数学模型，且参数辨识过程是一个复杂的数值过程，可能会遇到病态的数值问题，并且该标定 方法忽略了非几何误差因素的影响．因此，一些学 者[7-9]研究了包含非几何参数误差的新误差模型，采用模型参数辨识方法来标定．但是由于非几何误差参数的高度非线性及强耦合性，仅针对单个类型的非几何误差源的误差建模标定方法不具备通用理论指导性．为此，有学者提出了无需解析式误差模型和特定参数辨识方法的无模型标定方法．

由于无模型标定方法需要建立机构参数与参数误差之间复杂的非线性映射关系，人工神经网络因具有以任意精度逼近任意非线性函数的能力而逐渐被用于并联机器人的运动学标定中．径向基(radial basis function，RBF)神经网络[10]是一种前馈型神经网络，具有网络结构简单、学习速度快、非线性拟合能力强等优点，相较于反向传播(back propagation，BP)神经网络以及多层感知机(multilayer perceptron，MLP)等神经网络，RBF神经网络具有全局逼近能力，从根本上解决了局部最优问题，已被广泛应用于机器人运动学标定领域[11-13]．Yang等[11]提出了一种基于RBF神经网络的位移测量几何误差补偿方法，用于运动控制器中的误差补偿．Chen等[12]针对工业机器人存在的绝对位置精度低的问题，提出了一种误差相似性和RBF神经网络相结合的位置误差补偿方法．Yu[13]针对并联机器人非几何参数误差提出了一种由BP神经网络和RBF神经网络组成混合人工神经网络对并联机构进行位姿精度的补偿．

本文针对3-US/S并联平台的误差补偿问题，首先基于伪误差理论将因几何、非几何误差引起的末端姿态误差等效视为仅由驱动关节杆长误差所引起．进而采用RBF神经网络建立名义驱动关节变量与驱动关节杆长伪误差之间的非线性映射模型，并着重研究基于PSO算法的扩展参数和正则化参数的联合优化方法，以提升网络的泛化性能．最后通过运动学标定实验以及姿态稳定补偿实验验证了所提方法的正确性和有效性．

1 等效误差模型的构建

传统的运动学标定包括误差建模、误差测量、参数辨识、误差补偿4个环节，其中误差建模是机器人运动学标定流程中的首要环节．本节将以3-US/S并联机构为对象，在运动学分析的基础上建立用于标定的等效误差模型．

1.1 系统简介

3-US/S并联稳定平台的结构简图如图1所示，由静平台、动平台、3条US驱动支链和中央球铰约束支链组成．其中，US支链一端通过虎克铰与静平台连接，另一端通过球铰与动平台相连；中央立柱一端与静平台固定连接，另一端通过球铰与动平台中心相连．中央立柱限制了动平台的三向平动，通过控制3条US支链的伸缩量，即可实现动平台3个转动自由度的运动．

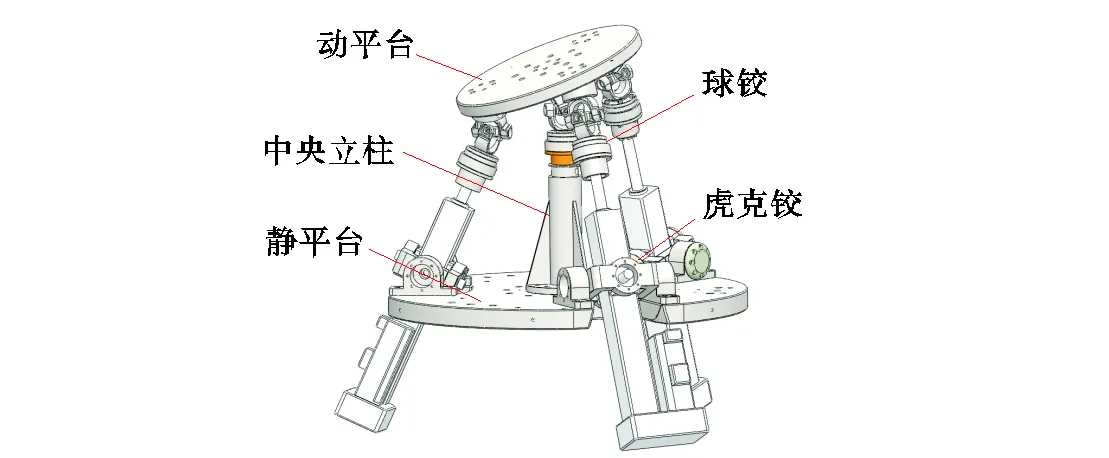
图1 3-UPS/S机构简图

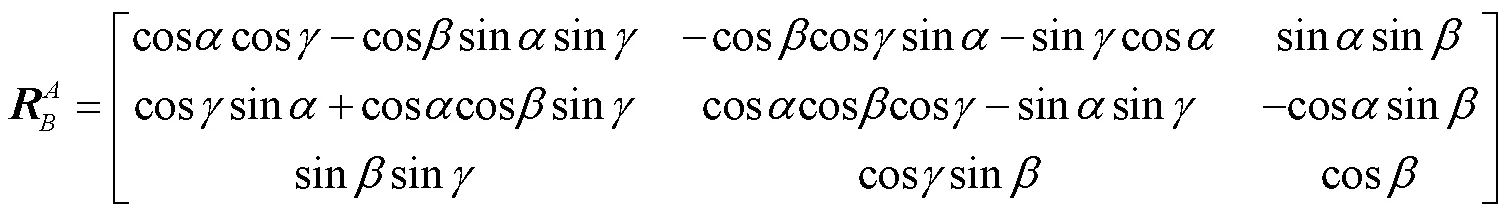
式中：表示方位角；表示倾斜角；表示扭转角.

1.2 位置逆解

在已知动平台姿态角的前提下，支链杆长计算 式为

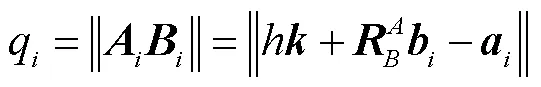
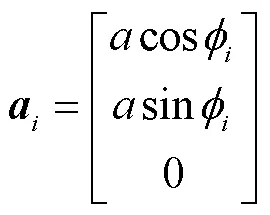
1.3 驱动关节等效误差模型

3-US/S并联稳定平台机构存在多闭环结构，误差源种类和数量较多，且存在耦合效应，难于建立完备的误差模型或准确辨识全部误差参数．考虑到所述并联机构具有三转动自由度，3个驱动关节为其运动生成元，因而动平台的姿态误差可视为仅由驱动关节的等效运动误差所生成，且该等效运动误差是机器人位形的函数．这样，基于机器人雅可比建立驱动关节等效误差与动平台姿态误差之间的映射模型，并采用神经网络方法建立驱动关节等效误差与理想驱动关节变量之间的非线性映射关系，即可实现全工作空间范围内动平台姿态误差的预测，并进而实施误差 补偿．

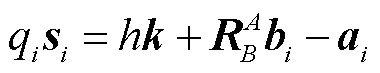
采用文献[22]中所提误差建模方法，可建立3-US/S机构的等效驱动关节误差模型为

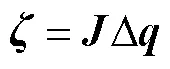
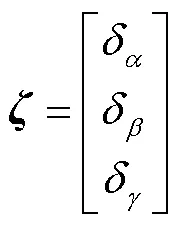
式(3)建立了机器人工作空间中姿态误差与关节空间中等效误差之间的映射关系，后序将通过该模型将仿真或实测末端姿态误差转换为关节空间等效杆长误差，并作为神经网络的输出，建立完整的误差 模型．

2 基于RBF神经网络的驱动关节等效误差预测方法

在关节空间中，名义驱动关节变量(理想杆长)与驱动关节等效误差之间的映射具有连续性，因此可将两者分别作为RBF神经网络的输入与输出，利用网络的非线性拟合能力实现驱动关节等效误差的预测，并进而通过修正驱动关节变量的方式补偿末端姿态误差．

2.1 基于RBF神经网络的标定方法

RBF神经网络是一种3层前馈型神经网络，在数学上可以看作一组加权径向基函数的线性组合，可以任意精度逼近任意连续函数[23]，由输入层、具有激活功能的隐藏层、输出层构成，其拓扑结构如图3 所示．

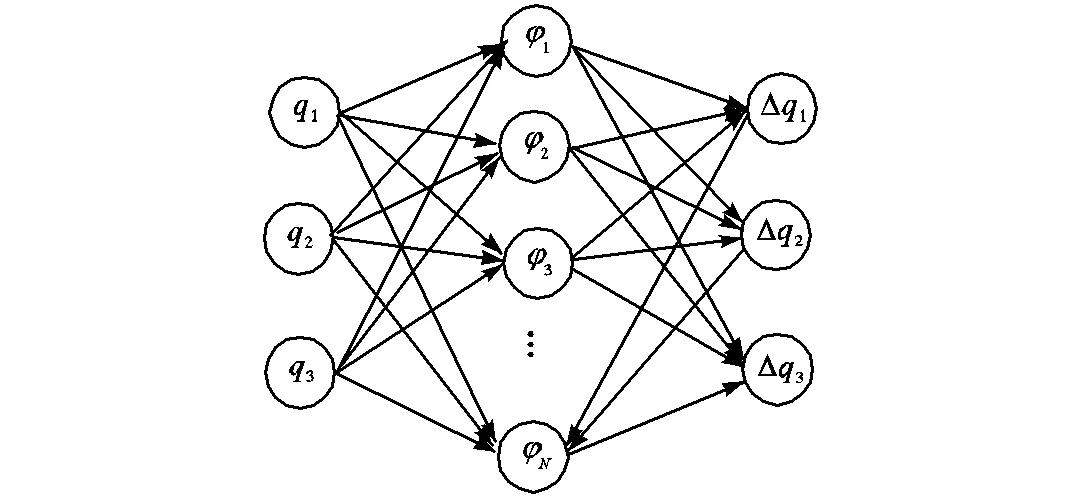
图3 RBF网络拓扑结构

应用于回归问题时，待拟合函数可直接用RBF神经网络近似为

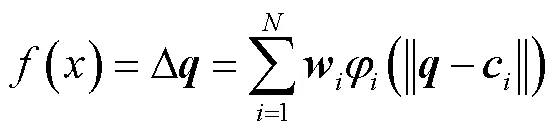
RBF神经网络的相关计算与基函数的选择有关，其非线性映射能力主要体现在隐层基函数上．考虑到高斯函数具有光滑性和无限可微性等优良特性，本文选取其作为网络的基函数．于是，网络可描述为

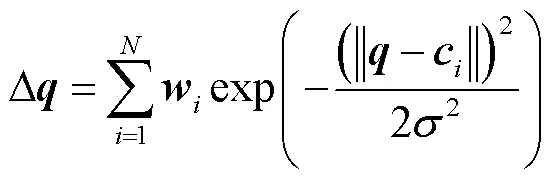
基于神经网络的运动学标定流程如图4所示，可分为4个步骤：

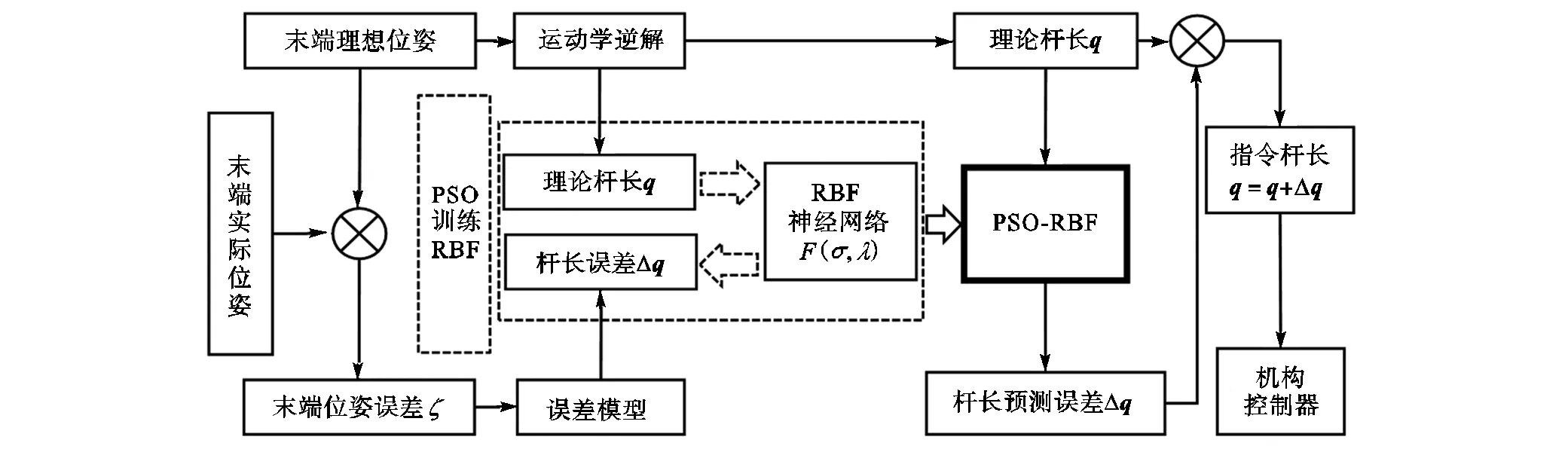
图4 神经网络标定流程

2.2 网络模型结构与参数初值的确定

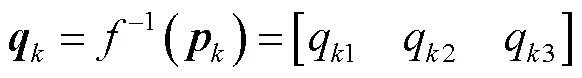
在非奇异位形，利用关节空间等效误差模型可以计算出驱动关节的等效误差为

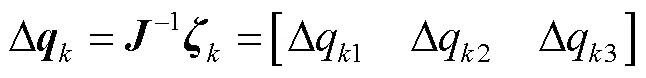
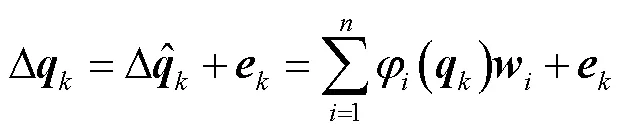
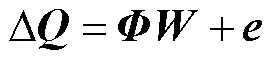
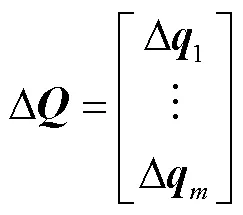
为解决训练数据噪声带来的网络过拟合问题，本文采用在损失函数中添加正则化项的方式改善网络的泛化性能[24]，相应的正则化误差准则为

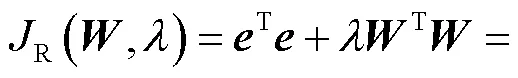
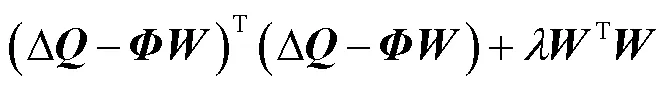
权重参数的表示方式为

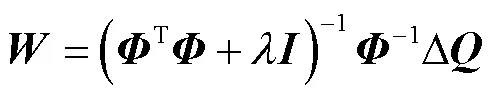
在RBF神经网络中，高斯基函数的特征主要由基函数的中心及扩展常数确定．隐层节点的选择是决定网络性能优劣的关键因素，虽然节点个数越多，RBF神经网络对于复杂系统的拟合能力越强，但是训练优化过程的复杂性以及网络过拟合的风险均会大幅增加[25]．对于3-US/S并联平台，经搜索计算发现，在工作空间均匀选取108个位姿点，并将其所对应的名义驱动关节变量作为网络中心点比较合适.继续增加中心点个数对RBF神经网络性能基本上没有帮助，且仿真研究表明，采用聚类算法对于中心位置进行训练对网络性能并无明显改善效果．

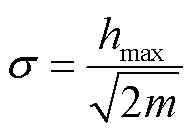
2.3 基于粒子群算法的网络参数优化

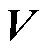
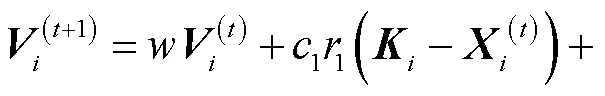
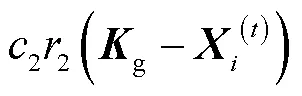
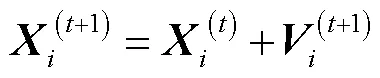
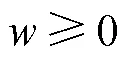
利用PSO算法对RBF神经网络进行全局优化的基本方法可以概括为：将RBF网络结构以及参数包含在一组变量中，定义RBF神经网络在训练集上的均方误差(mean square error，MSE)为优化目标，其值越小则网络的泛化性能越强，从而将神经网络训练问题转化为包含神经网络参数变量的目标函数优化问题．

结合粒子群算法和第2.2节提出的训练方法，本文提出一种二级分层训练方法，对这两个参数进行全局优化．如图5所示，在此过程中将网络的泛化性能作为这两个参数的适应度函数来进行检验，定义已知结构的RBF模型在测试集上的MSE为PSO算法的适应度函数，即

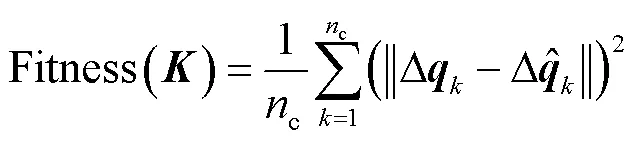
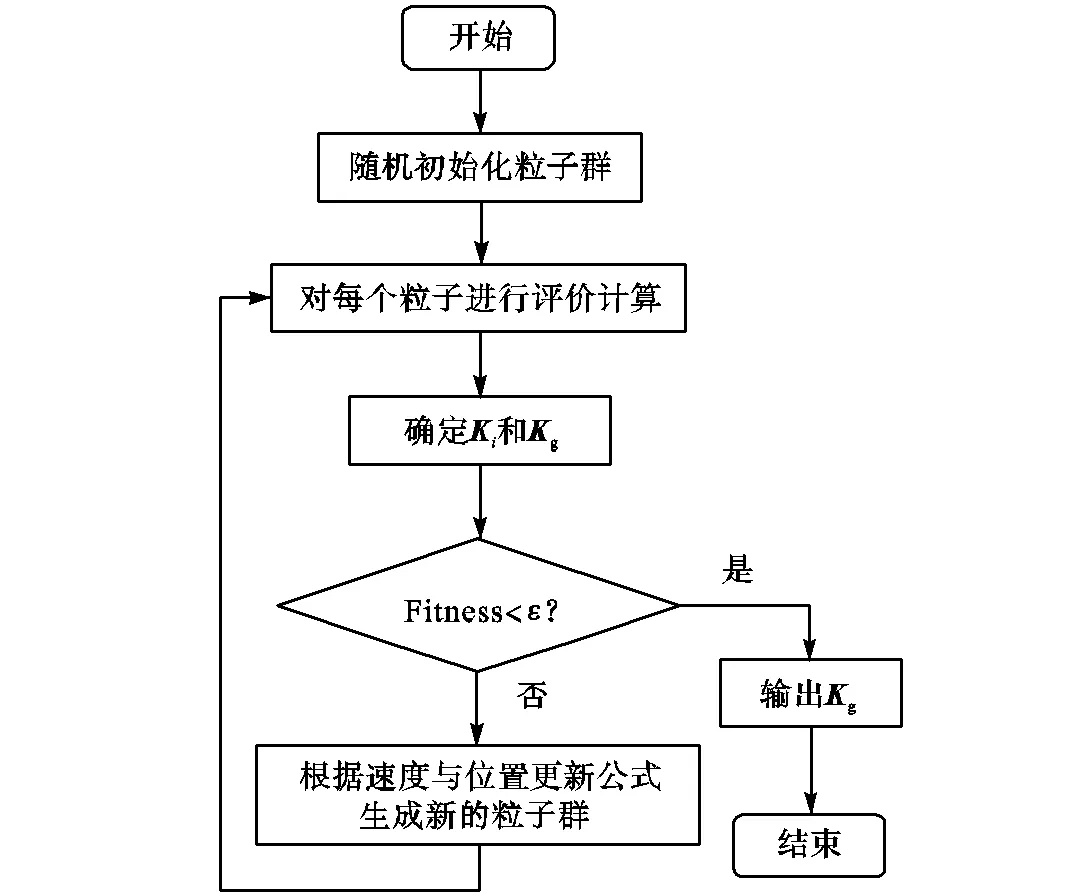
图5 扩展常数s与正则参数l的优化流程

由于PSO算法仅用于优化下层集成的RBF神经网络的2个参数，且下层为线性学习问题．因此相较于使用PSO对RBF所有参数进行直接优化，该方法能够更加高效地实现全局优化．

3 仿 真

本节将通过计算机仿真来验证所提出的RBF神经网络模型构造及训练方法的正确性及有效性，以及网络对驱动关节等效误差的预测效果．

3.1 仿真流程

仿真过程可分为如下步骤．

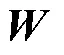
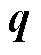
3.2 评价指标

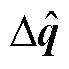
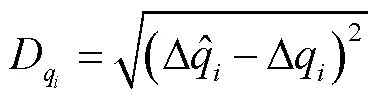
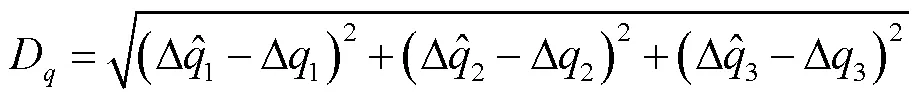
3.3 仿真结果分析

在完成网络模型结构构建与参数优化后，将利用验证集数据检验网络模型在关节空间中的预测能力．在验证位形下，对比未经PSO优化的RBF模型以及经PSO优化的PSO-RBF模型对于驱动杆误差预测能力，预测效果如图7所示，误差预测精度如图8所示．

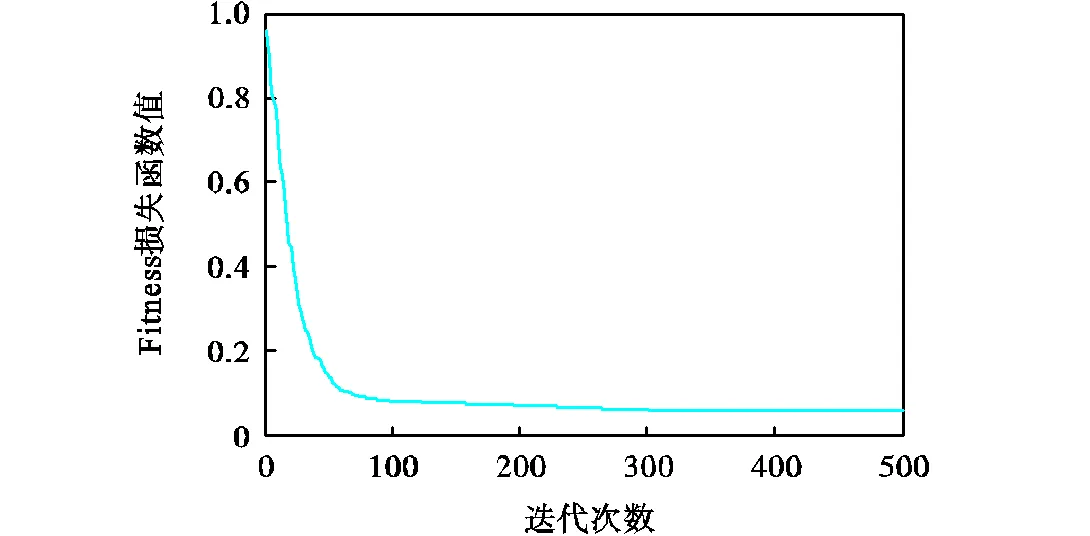
图6 PSO迭代收敛曲线

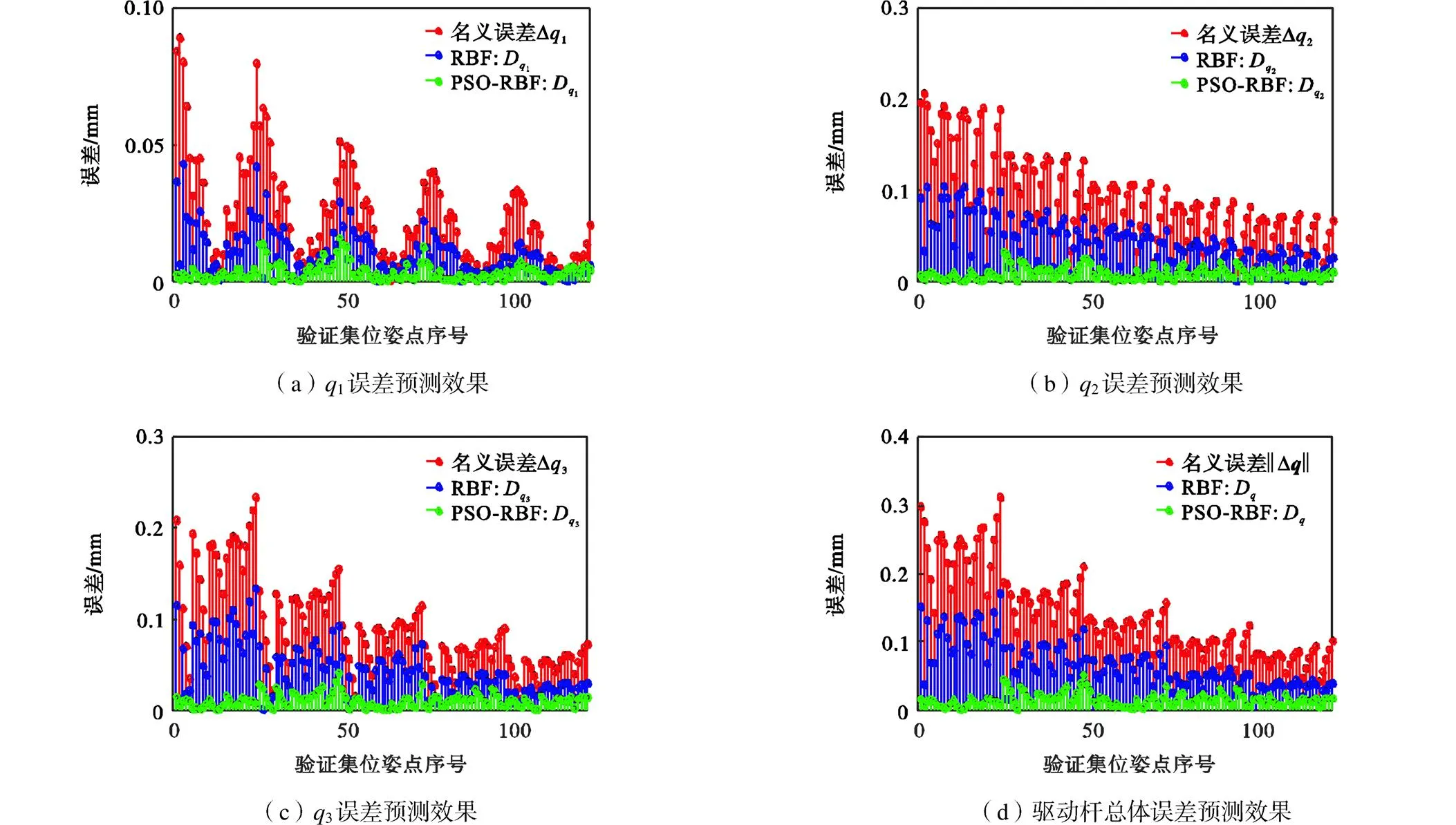
图7 误差预测效果对比

通过仿真结果可以看出，采用本文所提出的方法构建的PSO-RBF神经网络模型在关节空间中所展示出的误差预测规律与前述分析一致，证明了该方法的正确性与有效性．

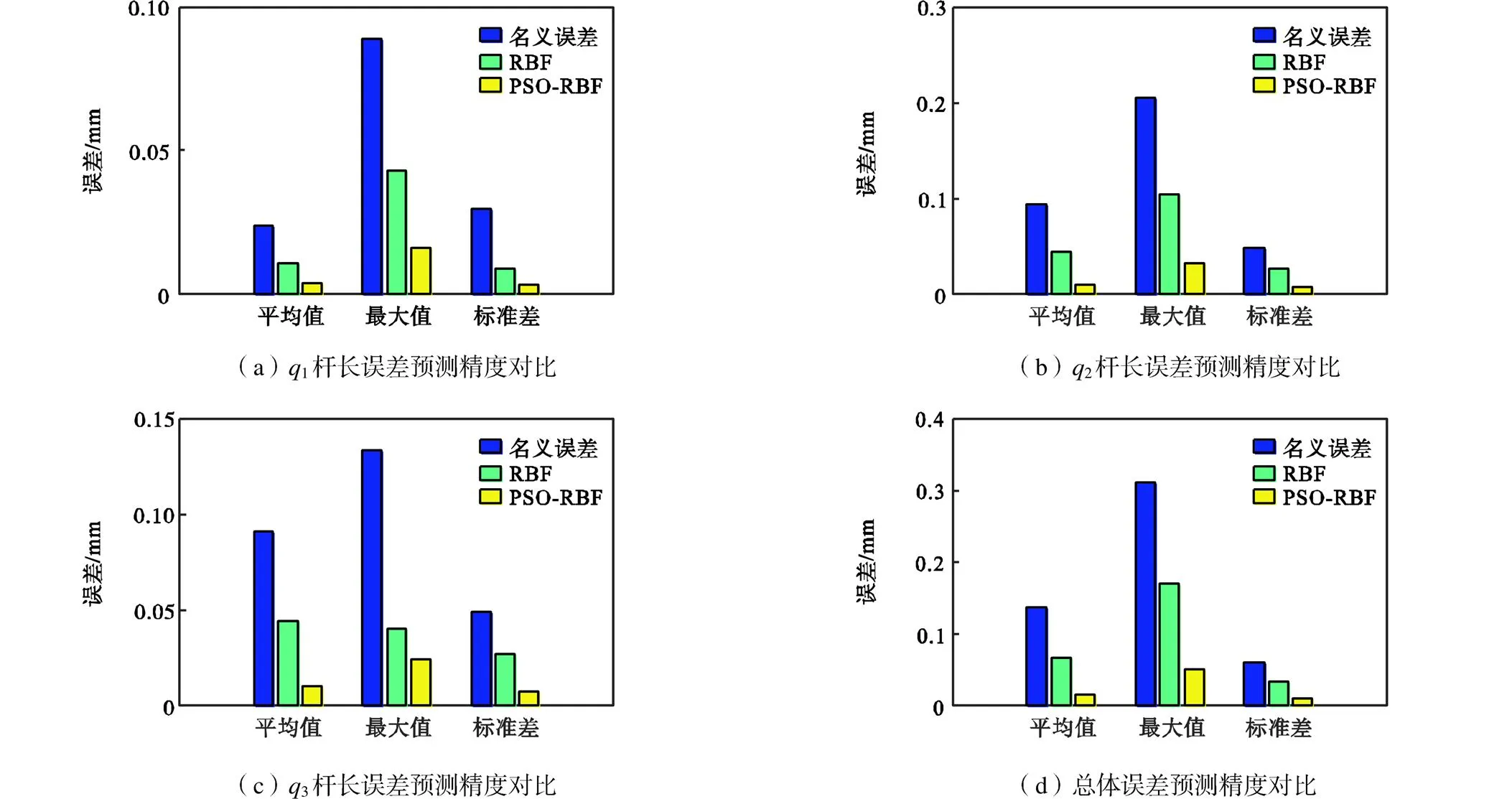
图8 误差预测精度对比

4 实 验

本节首先利用三坐标测量臂获取3-US/S稳定平台姿态误差信息，基于所提驱动关节等效误差模型实现稳定平台的运动学标定．而后，结合稳定平台应用场景，搭建姿态稳定补偿实验系统，研究标定前后的姿态稳定补偿效果，进一步验证所提方法的有效性.

4.1 姿态测量方案

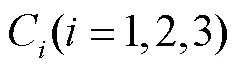
图9 测量系统

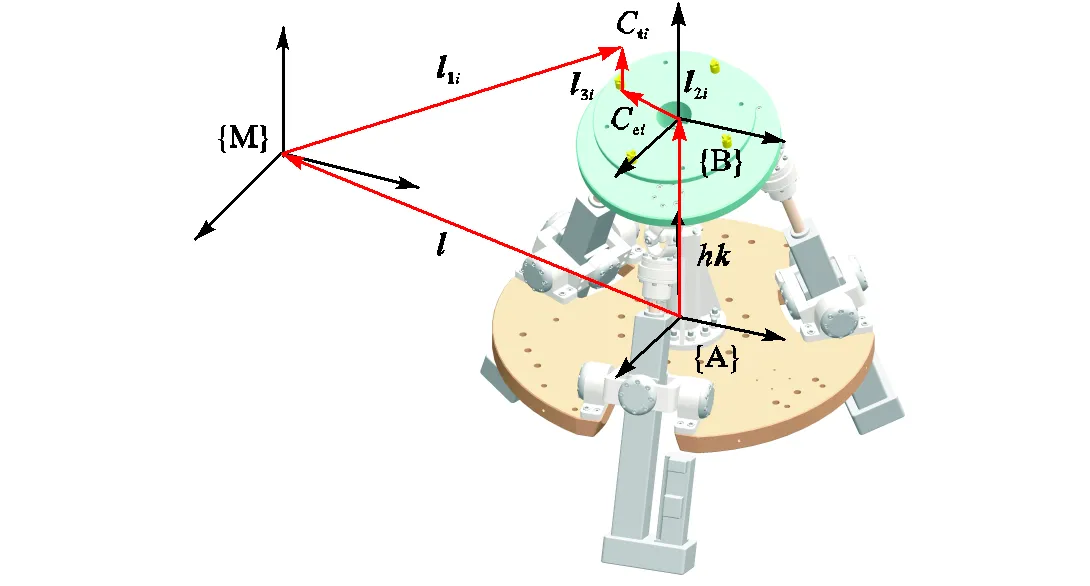
图10 三坐标测量臂测量原理

Fig.10 Measuring principle of coordinate measuring ma-chine

图11 工作空间测量位形分布

Fig.11 Configuration map of workspace measurement

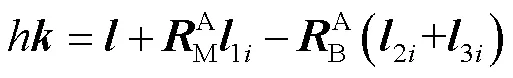
4.2 关节空间误差补偿实验

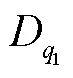
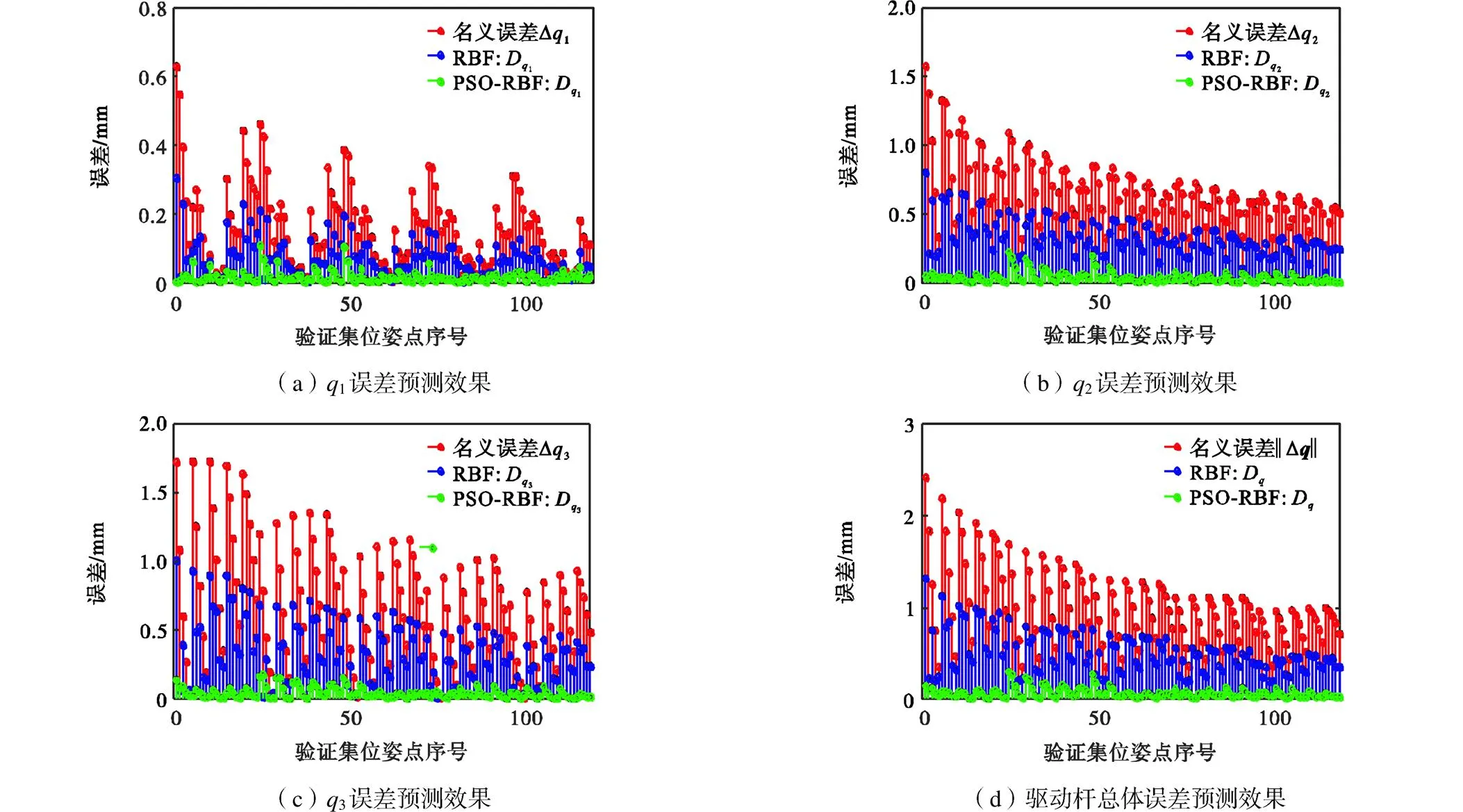
图12 关节空间误差预测效果对比

4.3 姿态稳定补偿实验

3-US/S并联稳定平台作为船载稳定平台用于补偿风浪流造成的船舶扰动，使稳定平台保持平稳．由于在船舶上进行实验成本较高，本文使用船舶模拟平台模拟海浪造成的船舶运动．实验装置如图14所示，稳定平台安装于船舶模拟平台之上，船舶模拟平台根据预设的指令曲线而动作，稳定平台根据倾角传感器测得的数据控制动平台姿态，使其相对地面的姿态保持水平．

稳定平台实验系统工作时，船舶模拟平台安装一个倾角传感器传输给稳定平台控制系统，解算出需要补偿的姿态角度，然后利用运动学逆解求出相应的驱动杆移动量，控制稳定平台进行实时的补偿运动．3个驱动杆的控制方法是基于位移传感器的位置反馈控制．同时，稳定平台上也安装一个倾角传感器，用于检测稳定平台补偿效果．

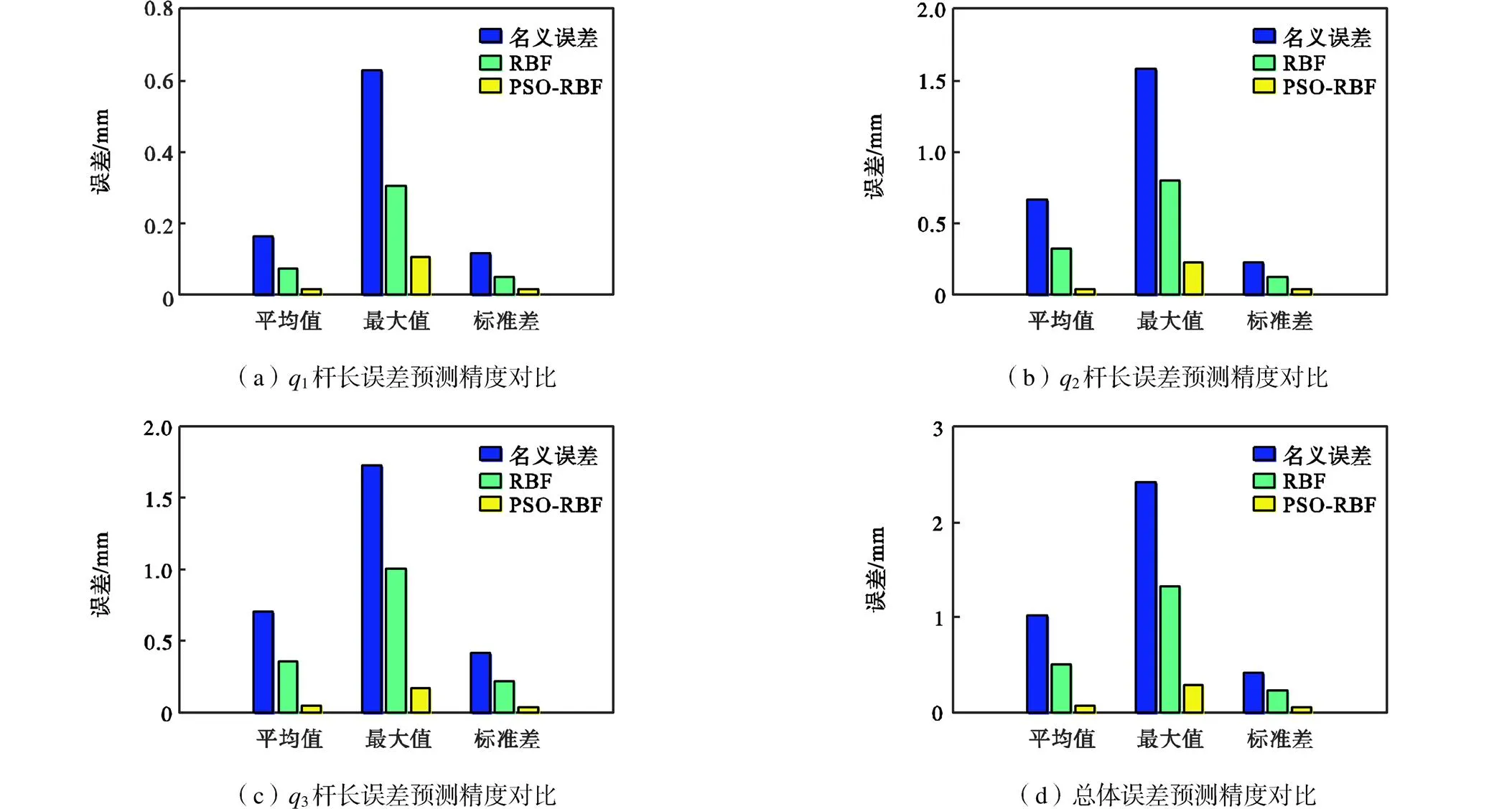
图13 关节空间误差预测精度对比

图14 稳定补偿实验系统

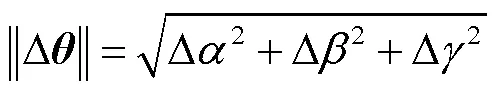
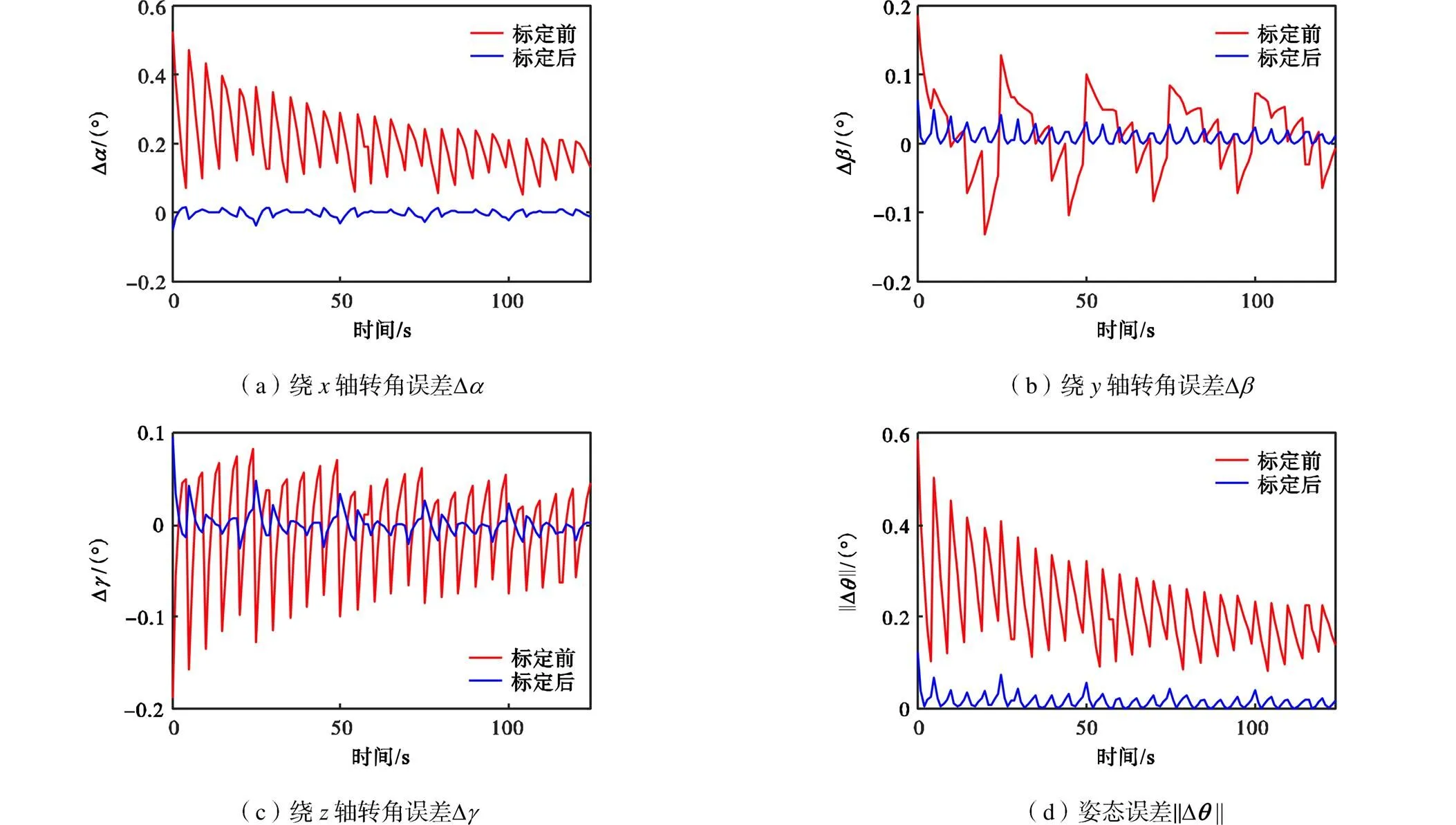
图15 稳定补偿实验效果

从测试结果可以看出，船舶模拟平台在125种固定姿态下，稳定补偿系统达到预定补偿效果，并且补偿后的结果稳定、波动较小．使用本文所提出的PSO-RBF方法在关节空间进行杆长误差补偿之后，可以实现该机构的精度提升，并提高姿态补偿效果．

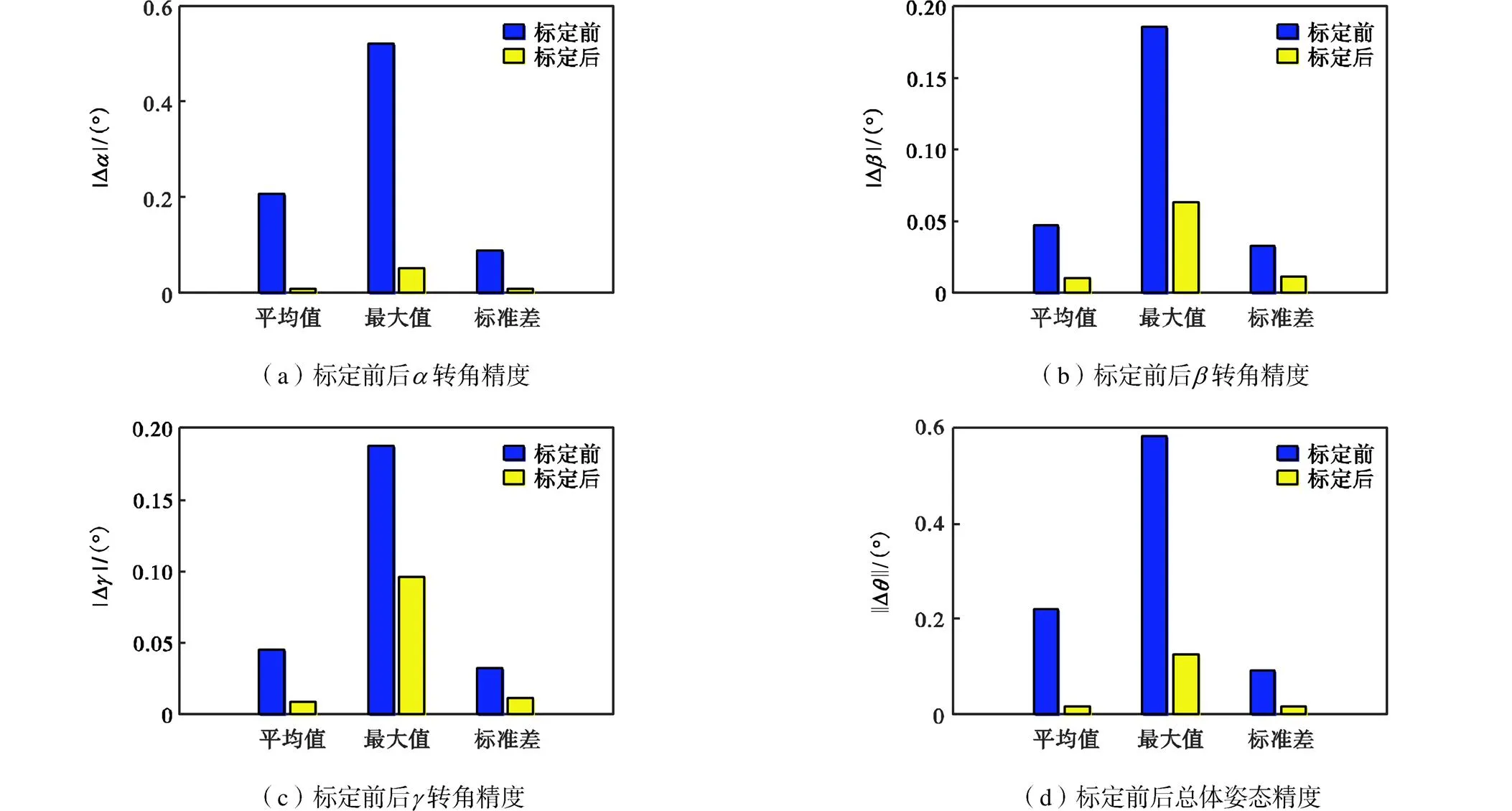
图16 标定前后转角精度对比

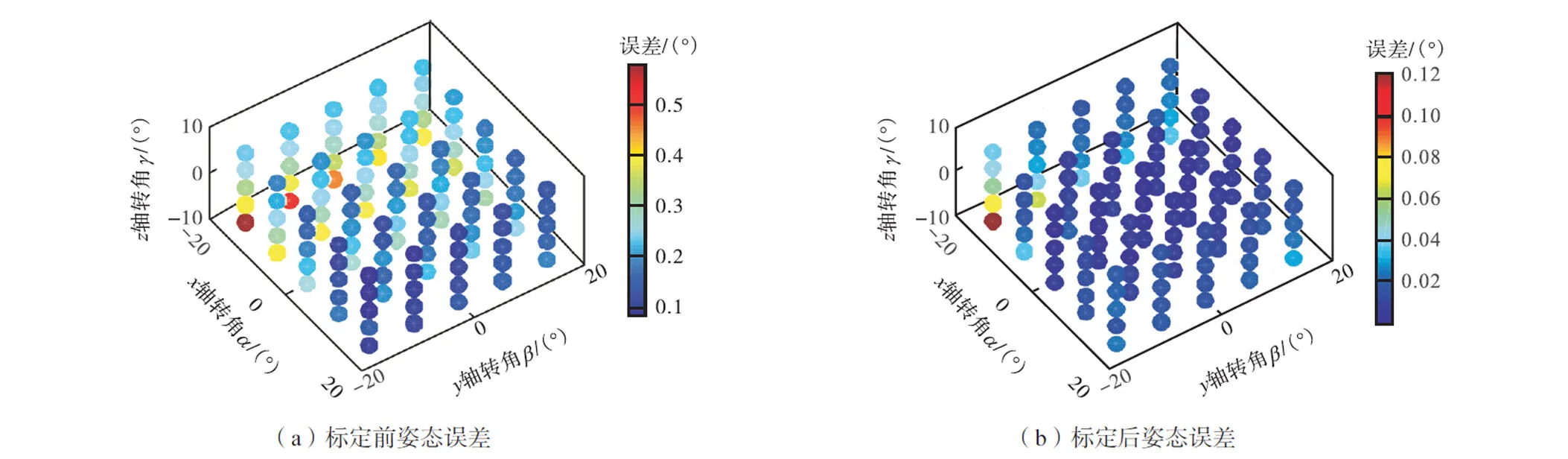
图17 标定前后验证位形姿态误差对比

5 结 论

针对传统运动学标定难以考虑非几何误差源的问题，本文基于等效误差模型并采用RBF神经网络方法研究了3-US/S并联机器人的标定方法，研究结论如下．

(1) 考虑各类非时变误差源对并联机构精度的影响，本文基于伪误差理论将因几何、非几何误差引起的末端姿态误差等效视为仅由驱动关节杆长误差所引起，进而采用RBF神经网络建立了名义驱动关节变量与驱动关节杆长伪误差之间的非线性映射模型．仿真及实验结果表明，所提方法具有高度的灵活性和适用性，可高精度刻画名义驱动关节变量与驱动关节杆长伪误差之间的映射关系，且网络输出变量可直接用于运动学标定，有效提升了标定效率与精度．

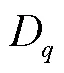
［1］ 王攀峰，王 星，郭 璠，等. 丝传动3-SPR并联机构运动学分析与力反馈控制[J]. 天津大学学报(自然科学与工程技术版)，2022，55(2)：184-190.

Wang Panfeng，Wang Xing，Guo Fan，et al. Kinematics analysis and force feedback control of wire-driven 3-SPR mechanism[J]. Journal of Tianjin University(Sci-ence and Technology)，2022，55(2)：184-190(in Chinese).

［2］ Nguyen H N，Le P N，Kang H J. A new calibration method for enhancing robot position accuracy by combining a robot model-based identification approach and an artificial neural network-based error compensation technique[J]. Advances in Mechanical Engineering，2019，11(1)：1-11.

［3］ Jang J H，Kim S H，Kwak Y K. Calibration of geometric and non-geometric errors of an industrial robot[J]. Robotica：International Journal of Information，Education and Research in Robotics and Artificial Intelligence，2001，19(3)：311-321.

［4］ Cong D，Yu D，Han J. Kinematic calibration of parallel robots using CMM[C]//2006 6th World Congress on Intelligent Control and Automation. Dalian，China，2006：8514-8518.

［5］ Lee S，Qiang Z，Ehmann K F. Error modeling for sensitivity analysis and calibration of the tri-pyramid parallel robot[J]. The International Journal of Advanced Manufacturing Technology，2017，93(5)：1319-1332.

［6］ Tian W，Yin F，Liu H，et al. Kinematic calibration of a 3-DOF spindle head using a double ball bar[J]. Mechanism & Machine Theory，2016，102：167-178.

［7］ Nubiola A，Bonev I A. Absolute calibration of an ABB IRB 1600 robot using a laser tracker[J]. Robotics and Computer-Integrated Manufacturing，2013，29(1)：236-245.

［8］ 张宪民，曾 磊. 考虑减速机背隙的3-RRR并联机构的运动学标定[J]. 华南理工大学学报(自然科学版)，2016，44(7)：47-54.

Zhang Xianmin，Zeng Lei. Kinematic calibration of 3-RRR parallel mechanism considering reducer backlash [J]. Journal of South China University of Technology (Natural Science Edition)，2016，44(7)：47-54(in Chinese).

［9］ Li T，Li F，Jiang Y，et al. Kinematic calibration of a 3-P(Pa)S parallel-type spindle head considering the thermal error[J]. Mechatronics，2017，43：86-98.

［10］ Broomhead D S，Lowe D. Multivariable functional interpolation and adaptative networks[J]. Complex Systems，1988，2：321-355.

［11］ Yang R，Tan K K，Tay A，et al. An RBF neural network approach to geometric error compensation with displacement measurements only[J]. Neural Computing and Applications，2017，28(6)：1235-1248.

［12］ Chen D，Wang T，Yuan P，et al. A positional error compensation method for industrial robots combining error similarity and radial basis function neural network[J]. Measurement Science and Technology，2019，30(12)：125010.

［13］ Yu D. A new pose accuracy compensation method for parallel manipulators based on hybrid artificial neural network[J]. Neural Computing and Applications，2021，33(3)：909-923.

［14］ Schwenker F，Kestler H A，Palm G. Three learning phases for radial-basis-function networks[J]. Neural Networks，2001，14(4/5)：439-458.

［15］ Wang W，Xu Z，Lu W，et al. Determination of the spread parameter in the Gaussian kernel for classification and regression[J]. Neurocomputing，2003，55(3/4)：643-663.

［16］ Niros A D，Tsekouras G E. A novel training algorithm for RBF neural network using a hybrid fuzzy clustering approach[J]. Fuzzy Sets and Systems，2012，193：62-84.

［17］ Ren Z，Li R，Chen B，et al. EEG-based driving fatigue detection using a two-level learning hierarchy radial basis function[J]. Frontiers in Neurorobotics，2021，15：618408.

［18］ Schwenker F，Kestler H A，Palm G. Three learning phases for radial-basis-function networks[J]. Neural Networks，2001，14(4/5)：439-458.

［19］ Niros A D，Tsekouras G E. A novel training algorithm for RBF neural network using a hybrid fuzzy clustering approach[J]. Fuzzy Sets and Systems，2012，193：62-84.

［20］ Kennedy J，Eberhart R. Particle swarm optimization[C]// Proceedings of International Conference on Neural Networks. Perth，Australia，1995：1942-1948.

［21］ 孙立军，刘 悦，童杰林，等. 基于科氏流量计和PSO-SVM的气液两相流测相研究[J]. 天津大学学报(自然科学与工程技术版)，2022，55(10)：1034-1044.

Sun Lijun，Liu Yue，Tong Jielin，et al. Gas-liquid two-phase flow measurement based on coriolis flowmeters and PSO-SVM[J]. Journal of Tianjin University(Science and Technology)，2022，55(10)：1034-1044(in Chinese).

［22］ Mohanta J K，Mohan S，Huesing M，et al. Error modelling and sensitivity analysis of a planar 3-PRP parallel manipulator[C]//Computational Kinematics. Poitiers，France，2018：315-322.

［23］ Park J，Sandberg I W. Universal approximation using radial-basis-function networks[J]. Neural Computation，1991，3(2)：246-257.

［24］ Huang T，Zhao D，Yin F，et al. Kinematic calibration of a 6-DOF hybrid robot by considering multicollinearity in the identification Jacobian[J]. Mechanism and Machine Theory，2019，131：371-384.

［25］ Chen S，Chng E S，Alkadhimi K. Orthogonal least squares learning algorithm for radial basis function networks[J]. IEEE Transactions on Neural Networks，1991，64(5)：829-837.

［26］ Song Y，Wang P，Yang B. An improved RBF neural network with the adaptive spread coefficient[C]// Proceedings 7th International Conference on Signal Processing. Beijing，China，2004：1526-1529.

Kinematics Calibration of 3-US/S Stabilized Platform Based on RBF Neural Network

Tian Wenjie1，Zhao Kun1，Zhang Xilin2，Wang Lina2，Zhang Xiangpeng1

(1. School of Marine Science and Technology，Tianjin University，Tianjin 300072，China；2. School of Mechanical Engineering，Tianjin University，Tianjin 300350，China)

The three-degree-of-freedom parallel configuration stability platform is used as a ship stability platform to compensate for ship disturbances. Attitude accuracy is one of the important performance indexes in parallel configuration attitude stabilization platforms. Due to the strong coupling and nonlinear between geometric and non-geometric error sources in the mechanism，it is difficult to establish an error model containing all error sources for kinematics calibration. To solve this problem，this paper proposed a joint space error compensation method based on the equivalent error model and RBF neural network. First，according to the pseudo-error theory，we considered the attitude error of the mechanism moving platform caused by geometric and non-geometric errors as the equivalent error only caused by the length error of the driving joint. Then，the RBF neural network was used to establish a nonlinear mapping model between the nominal driving joint variables and the pseudo-errors of the driving joint length. Furthermore，we designed a two-level hierarchical network training method to improve the generalization performance of the network and the prediction accuracy of the attitude error of the moving platform. The lower layer constructed the network linear structure，and the upper layer used the particle swarm optimization(PSO)algorithm to globally optimize the network expansion constant and regularization parameters. Finally，PSO-RBF was used to conduct the simulation of joint space equivalent error prediction and the experimental study of operating space error compensation on the 3-US/S parallel attitude stabilization platform. The results show that the proposed method has high flexibility and applicability and can accurately describe the mapping relationship between nominal driving variables and driving joint length pseudoerrors. Moreover，the network output variables can be directly used for kinematics calibration. The bar length accuracy in the joint space is increased by 93.6%，and the posture accuracy in the operating space is increased by 92.3%，which effectively improves the calibration efficiency and accuracy and verifies the correctness and effectiveness of the proposed method.

attitude stabilized platform；kinematics calibration；pseudo-error model；RBF neural network；PSO algorithm

10.11784/tdxbz202206006

TP242

A

0493-2137(2023)09-0985-13

2022-06-05；

2022-09-10.

田文杰（1986— ），男，博士，副教授.Email：m_bigm@tju.edu.cn

田文杰，wenjietian@tju.edu.cn.

天津市企业科技特派员项目(20YDTPJC01010)；国家重点研发计划资助项目(2022YFC3006000).

the Enterprise Science and Technology Specialists Project of Tianjin，China(No. 20YDTPJC01010)，the National Key Research and Development Program of China(No. 2022YFC3006000).

(责任编辑：王晓燕)