干散货运价指数内生发展趋势研究

宋凌玉　林辉民

【摘 要】 基于主变量分析理论改进系统动力学（SD）模型，应用SD因果与相关关系回路图划定干散货航运系统边界，分析引发干散货运价指数（BDI）周期性波动的主变量之间的回归关系，建立SD内生动态预测模型以推演BDI指数的变动，就其走势做出方向性判断。研究发现，预测模型内部供需所产生的内生力会推动BDI在2022年出现一波较大的运价走低行情，而后2～3年干散货运价处于本轮中周期的繁荣后期阶段，之后进入下一个中周期的衰退阶段。

【关键词】 干散货航运市场；干散货运价指数；内生动态预测模型

0 引 言

国际航运市场在世界贸易中占有重要地位，而其中的干散货航运市场又是规模最大、发展最成熟的细分航运市场，受经济周期、各种突发事件等影响，较难准确预测干散货航运市场运费的变动。波罗的海干散货运价指数（Baltic Dry Index，BDI）由若干条主要航线即期运费加权计算而成，是衡量干散货航运市场的权威指数，也是反映全球贸易和经济趋势的重要先行指标[1]。尤其在未来一段时间，全球贸易和经济格局处在重要的转折点，该指数更是受到航运界经营者及相关贸易商的广泛关注，BDI也是各航运企业做出投资决策的主要依据。

系统动力学（System Dynamics，SD）建立在整体系统视角上，以系统内部信息反馈控制为基础[2]，以动态性、相关性和联系性考虑问题。系统的行为模式主要取决于其内部的动态结构和反馈机制，有利于充分考虑相关因素，以及各因素之间相互动态变化产生的系统变化。对于系统动力学在干散货航运系统中的运用，已有文献更多倾向全面描述干散货航运系统，用于测试参数变动对干散货航运系统的影响，但系统边界较广，无清晰区分内、外生变量，也未能模拟干散货航运系统内生結构。

主变量分析法是利用统计学分析各变量影响程度的一种统计方法，其数学运算主要建立在矩阵运算的基础之上，并假定变量之间呈线性关系[3]。本文基于主变量分析理论，改进了系统动力学模型，创立主变量-系统动力学模型；以BDI指数为标识，着重市场供需基本面分析，通过SD因果与相互关系回路图分析干散货航运市场背后的周期性规律，进而利用主变量分析法研究干散货运价指数波动的主要内生影响因素，并将这些因素作为变量，利用SD存量流量图模拟各因素与BDI指数之间的相互作用机理，从量化角度建立参数表达式方程组，通过SD内生动态预测模型预测未来BDI的发展趋势，这对航运市场中各方在今后运力发展战略规划及运营风险规避具有十分积极的作用。

1 基于主变量-SD的内生动态 预测模型

1.1 干散货航运系统内生结构模型建模思路

（1） 本文预测未来3～5年BDI的内生发展趋势。内生是指干散货航运系统中各内生变量之间的交互作用最终产生干散货运价周期性波动的动态行为。面对该问题，应确定干散货航运系统边界，绘制其因果与相互关系回路图，确定主要内生变量，以便进行主变量分析。

（2） 借助时间序列关系图形分析主要内生变量之间的动态行为关联。以各主变量为因变量，通过系统因果回路图寻找与其存在因果关系的自变量，形成自变量集合{x1，x2，…，xk}，依据多元线性回归模型可得表述如下：

（3） 根据上述回归关系，以内在反馈和SD流图的形式提出干散货航运系统SD内生动态预测模型。通过数据测试，并不断简化整个内生模型，仅保留可预测干散货运价的基本特性。

1.2 干散货航运系统边界及主要内生变量确定

有文献表明BDI的波动存在周期性，其本质表现为干散货航运市场的周期性，一般历经繁荣、衰退、萧条和回复4个循环阶段，不同影响因素造成BDI在不同时间维度上的周期性波动。关于干散货航运市场周期划分及其影响因素，STOPFORD[4]认为，航运周期中存在60年长周期成分、5～10年短周期成分和1年以内季节成分；余方平等[5]认为BDI长周期平均周期时长约为16年，中周期平均周期时长约为2～4年，短周期平均周期时长为0.4～0.6年；武华华等[6]认为，BDI中周期时长约为10年，短周期时长约为4年，季节周期时长约为1年。

本文将影响干散货航运运价波动的因素划分为4个层面：① 季节性波动层面，时间跨度为1年，主要由四季和海洋气候等自然条件、干散货运力和需求的不可储存性、运费衍生品投机交易等因素综合决定； ② 短周期层面，时间跨度约为2～4年，主要由干散货船舶运力供给、航运企业竞合及投资偏好、航运成本等调整时间较短的供给侧因素综合决定； ③ 中周期层面，时间跨度约为10年，主要由全球经济发展状况、干散货海运贸易流的规模和结构等需求侧的因素综合决定； ④ 长周期层面，时间跨度约为20～60年，主要由长期技术、社会、经济或区域变化驱动。

将干散货航运市场看作统一的系统，综合考虑其在4个层面的影响因素，发现要预测未来3～5年BDI的发展趋势，应立足于短期和中期。综上所述，干散货航运市场的供给与需求关系在系统中占主要地位。因此，干散货航运系统应包括供给和需求2个部分，供给侧反映的是干散货航运市场自身规模的发展，即干散货船运力变动情况；需求侧反映的是国际干散货贸易的发展，即大宗干散货如粮食、铁矿石、煤炭等及其他小宗干散货的海运周转量。运用SD因果与相互关系回路图分析整个干散货航运市场，如图1所示。随着干散货海运贸易量增加，BDI上涨，运价上涨带来新船投资增加和旧船拆解减少，造成BDI下跌。BDI的涨跌取决于干散货航运市场供给与需求的比值。随着供需比上涨，BDI上涨，上述过程为因果回路1。本文在通常供需比T/F的基础上增加了另一条因果回路2，引入修正供需比T/F*。因为一般情况下，供需比T/F只考虑了目前干散货航运市场上存在的所有船舶，未考虑到不是现有运力都会参与运输，只有活跃的在运运力才真正构成了干散货航运市场的供给。

因系统边界内应形成闭环回路，由图1可确定干散货航运市场主要内生变量应包括：供需比T/F和修正供需比T/F*，新交船运力占比D/F，拆船运力占比S/F，新造船订单占比N/F，压港船舶占比C/F，闲置船舶占比I/F。外生变量为受世界宏观经济影响的干散货海运贸易量T。上述因素与BDI指数相互作用，维持着干散货航运市场的动态平衡。

1.3 干散货航运系统主要内生变量及相关关系

（1）供需比T/F和修正供需比T/F*的计算公式分别为：T/F＝干散货海运周转量（Tm） / 干散货船现有总运力（F）；T/F*＝干散货海运周转量（Tm） / 干散货船在运总运力（AF）。T/F、T/F*与BDI对比如图2所示，由图2可知，在供需比T/F和修正供需比T/F*上扬时，BDI随之上涨，三者的涨跌趋势相同。

（2）D/F即新交船运力占比，表示每年度新造干散货船交付的运力（D）占干散货船现有总运力（F）的比值，其计算公式为：D/F＝干散货船新交船运力（D） / 干散货船现有总运力（F）。D/F与BDI对比如图3所示，由图3可知，当BDI指数上涨达到高位后，经过3～4年时间的延迟，D/F值会有相应幅度的提高，而在BDI下探的年份，D/F值也会相应走低。而D/F上扬，新交船数量增加会影响BDI，使其后续走低。

（3） S/F即拆船运力占比，表示每年度干散货船拆解运力（S）占干散货船现有总运力（F）的比值，其计算公式为：S/F＝干散货船拆解运力（S） / 干散货船现有总运力（F）。S/F与BDI对比如图4所示，由图4可知，BDI走高的年份，干散货船拆船比例S/F会降低，而当BDI指数走低的时候，干散货船拆船比例S/F会有所升高，两者呈反向涨跌趋势。

（4） N/F即新造船订单占比，表示每年干散货船新造船订单运力（N）占干散货船现有总运力（F）的比值，其计算公式为： N/F＝干散货船新造船订单运力（N） / 干散货船现有总运力（F）。N/F与BDI对比如图5所示，由图5可知，BDI指数走高的年份，N/F会相应上升，而当BDI指数走低的时候，N/F会随之下降，两者涨跌趋势相同。

（5）C/F即压港船舶占比，表示每年度干散货船在港口处于拥堵等待状态的船舶平均运力（C）占干散货船现有总运力（F）的比值，其计算公式为： C/F＝干散货船压港船舶运力（C） / 干散货船现有总运力（F）。C/F与BDI对比如图6所示，由图6可知，BDI指数走高的年份，C/F会相应上升，而当BDI指数走低时，C/F随之下降，两者涨跌趋势大体相似，呈非线性相关趋势。

（6） I/F即闲置船舶占比，表示每年度干散货船因封存、修理或另作他用而闲置的船舶平均运力（I）占干散货船现有运力（F）的比值，其计算公式为： I/F＝干散货船闲置船舶运力（I） / 干散货船现有总运力（F），I/F与BDI对比如图7所示，由图7可知，BDI指数走高的年份，I/F会相应降低，而当BDI指数走低时，I/F会随之上升，两者涨跌趋势相反。

1.4 干散货运价指数BDI内生动态预测模型确立

根据相关文献可知，BDI预测模型除选取供需方面的变量外，多会选取如燃油价格、货币市场指数（如道琼斯指数、纳斯达克指数或美元指数）等，但文献只为探求BDI波动的内生趋势，因此尚未考虑上述外部影响因素，仅专注于内生变量之间的相互关系，以明确产生干散货运价波动的内生性解释。本文以年为时间单位，选取1999―2021年数据，共26组变量，598个数据，来源于Clarkson Intelligence及OECD数据库，部分缺失数据，通过数学推导、回归分析等予以补全。

根据图1中影响BDI波动的2条因果关系回路可知，存在如下2种针对被解释变量BDI的解释变量集合。

针对回路1，即第1种解释变量集合f （IBDI）＝f （T，Rt，F，T/F，S，S/F，N，N/F，D，D/F）。首先，通过t檢验法决定解释变量的取舍，每次删除收尾概率p最大的解释变量，依次删除Rt，T，N/F，D，S，S/F，D/F，直至所有解释变量通过回归系数的显著性检验，得到多元线性回归方程如下：

其次，分别计算各自变量的方差膨胀因子，依次剔除nVIF值最大的自变量，确保剩余自变量膨胀因子不大于5，可得以下表达式：

采用式（4）构建SD流图，不满足系统动力学建模的模型结构适合性检验和模型行为适合性检验，且拟合结果明显不符合实际，是伪回归，因此以式（5）为基础，依据因果回路1构建SD内生动态预测模型1，如图8所示。

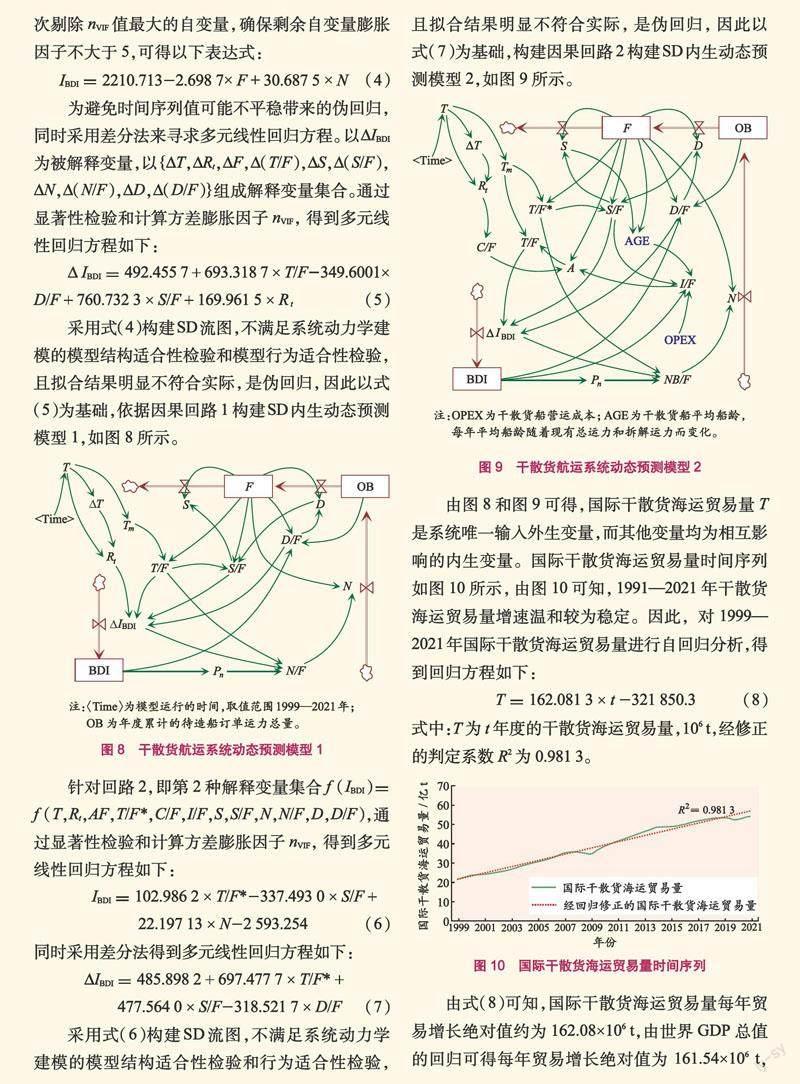
采用式（6）构建SD流图，不满足系统动力学建模的模型结构适合性检验和行为适合性检验，且拟合结果明显不符合实际，是伪回归，因此以式（7）为基础，构建因果回路2构建SD内生动态预测模型2，如图9所示。

由图8和图9可得，国际干散货海运贸易量T是系统唯一输入外生变量，而其他变量均为相互影响的内生变量。国际干散货海运贸易量时间序列如图10所示，由图10可知，1991―2021年干散货海运贸易量增速温和较为稳定。因此，对1999―2021年国际干散货海运贸易量进行自回归分析，得到回归方程如下：

式中：T为t年度的干散货海运贸易量，106 t，经修正的判定系数R2为0.981 3。

由式（8）可知，国际干散货海运贸易量每年贸易增长绝对值约为162.08？06 t，由世界GDP总值的回归可得每年贸易增长绝对值为161.54？06 t，两者预测结果接近，因此本文采用该自回归方程。

2 干散货航运市场内生动态模型模拟结果分析

经过模型结构适合性检验和模型行为适合性检验（含量纲一致性、参数灵敏度等检验）后，内生预测系统内部干散货运价在与新交运力、拆解运力等内生因素的交互影响下，形成市场平衡内生力，造成BDI运价产生周期性上下波动，BDI Ⅰ为回路1的模拟结果，BDI Ⅱ为回路2的模拟结果。

（1） 回路1模型与回路2模型均模拟出了BDI涨跌形势和周期。以波峰到波峰為一个周期，大致可以分为3个周期：2004年之前，2004年左右―2015年左右，2015年左右―2025年左右，大约10年为一个长周期。由于模型只考虑了主要内生变量，未考虑其他影响运价波动的外生因素，因此拟合指数和实际指数对比，模拟结果明显起涨较早，跌幅更大，反弹也更明显，时间前后差异比较明显，但在长周期时间上基本相同。

（2） 拟合值和真实值存在差异，由于现实航运市场中缓冲因素较多，如运价开始上涨时，船东可以采取提高船速、选用路程更短的航运路线、减少修理、启用封存船舶、将挪作他用的船舶重新投入市场、推迟拆解船舶等方式增加船舶运力供给，使得运价上涨变慢；面对运价下跌时，可以通过降低船速、封存或闲置船舶、卖出二手船或拆解船舶等方式减少船舶运力供给，减小运价跌幅。但在模型中，很多因素无法量化模拟，与真实值相比，模拟结果波动幅值更大，涨跌更急。

（3） 对比BDI Ⅰ与BDI Ⅱ可知，BDI Ⅰ起涨更早，BDI Ⅱ起涨稍晚，这是因为BDI Ⅱ第2条回路采用修正供需比T/F*，在模型中多考虑了因贸易繁荣带来海运贸易量增加导致的船舶压港因素，以及因价格下跌导致的船舶封存、安排修理或另作他用带来的船舶闲置因素，使得BDI Ⅱ存在较多缓冲因素，更贴近真实BDI的走势。后续研究可以在内生模型中加入更多内生缓冲因素，使模拟结果更贴近真实运价波动。

（4）模型数据剔除了新冠疫情带来的2020年和2021年船舶压港严重的异常值。在没有新冠疫情的情况下，系统内生趋势会使得BDI在2021年后开始上涨。但由于2019年末疫情暴发，使得干散货航运市场受外来因素影响，导致运力短缺加剧，BDI在2020年开始上扬。在新冠疫情对航运的影响逐步减弱后，运价走低也会提前到来。

（5） 在没有“黑天鹅事件”发生的情况下，内生预测模型内部供需所产生的内生力会推动BDI在2022年有一波较大的运价走低行情，推测而后2～3年处于回升或者震荡徘徊于波峰。目前，运价处于该长周期的繁荣后期，在波峰徘徊后，会进入下一个长周期的衰退阶段，转入下降通道。

3 结 语

2022年，干散货航运市场运价有较大的下降调整，其后2～3年内市场整体呈恢复上行趋势，处于本轮中周期的繁荣后期阶段。该结论可为船东扩张运力提供参考，如为规避市场风险，扩张运力需锁定中长期租约，这样才能抓住市场机遇。中期来看，干散货航运市场将在结束本轮繁荣后期阶段后进入下行通道，即进入下一个中周期的衰退阶段。武华华等[6]认为约10年为一个周期长度。本文通过计算可得，2024年左右干散货航运市场达到本周期顶峰，其后进入下一周期，结论与文献[6]基本相同。

参考文献：

[1] 王大山，刘文白. 国际干散货航运市场发展及BDI指数预测研究――基于联立方程模型的分析[J]. 价格理论与实践，2018（6）：78-81.

[2] 王其藩. 系统动力学[M]. 北京：清华大学出版社，1994．

[3] 王大山，刘文白. 国际干散货航运市场发展趋势研究――基于主变量-自回归模型的分析[J]. 技术经济与管理研究，2021（4）：83-88.

[4] STOPFORD M. Maritime economics 3e[M]. 3rd ed. London： Taylor & Rrancis， 2008.

[5] 余方平，匡海波. 基于VMD-GRGC-FFT的BDI指数周期特性研究[J]. 管理评论，2017（4）：213-225.

[6] 武华华，匡海波，孟斌，等. 基于EMD-WA模型的BDI指数波动周期特征研究[J]. 系统工程理论与实践，2018（6）：1586- 1598.