基于K-means聚类与PLS回归模型的交通速度短时预测

贾秀燕　孙秋霞　李勍

摘要：为实现对交通流局部特征的有效提取，提高交通速度预测模型的可解释性，提出基于K-means聚类与偏最小二乘（Partial Least Squares，PLS）回歸的交通速度短时预测模型。模型采用时空相关矩阵挖掘路网中相邻路段交通速度之间的关联性，利用K-means聚类算法划分历史数据集，并选取实测出租车GPS数据验证模型对交通速度短时预测的准确性。实验结果表明，与ARIMA、PLS回归和LSTM模型相比，该模型的预测误差减少了约30%。

关键词：城市交通；速度短时预测；K-means聚类；偏最小二乘回归；时空相关矩阵

中图分类号：U121 文献标志码：A

随着中国机动化进程不断加快，高峰出行困难成为大中城市所普遍面临的难题。作为智能交通运输系统的一项重要功能，交通控制与诱导调控策略的制定主要依赖于交通速度预测的结果。交通速度预测按照预测时间窗的长度通常划分为长时预测和短时预测，长时预测的时间步长通常以日、月或年计算，短时预测更倾向于对交通状态的微观描述，观测时间通常小于15min［1-2］。预测短时交通速度，实时评价交通状况，能够起到疏导交通拥堵、减少环境污染和驾乘人员等待时间、提高交通参与者的安全、为驾驶人提供有效出行信息服务的作用。国内外学者利用各学科领域内的知识开发了各种用于短时交通速度预测的方法，这些方法大致分为两大类：经典方法和基于深度学习的方法。经典预测方法包括统计方法和传统的机器学习方法［3］。统计方法假设未来数据与历史数据具有相似性，通过建立数据驱动的统计模型对交通速度分析预测，而交通速度数据具有复杂的非线性特征，往往不满足统计方法的假设，且这些方法多适用于小数据集［4-5］。传统的机器学习模型整体的非线性有限，预测效果并不是最佳的［6-8］。深度学习的出现使人工智能在交通速度预测的潜能得到进一步开发［9-14］。在数据集有限的应用情景下，深度学习模型难以有效的挖掘数据的规律，同时具有计算复杂度高、可解释性差的缺点。为了实现交通流量、交通速度、行程时间的短时预测，将多个模型组合以提升模型预测性能［15-17］。模型的组合方式、权重参数的确定以及训练数据集的平衡问题是组合模型研究中的难点［18-19］。为了克服传统模型无法有效提取交通速度数据非线性特征这一缺点，本文聚焦路网交通速度之间关联性的挖掘，建立时空相关矩阵，利用K-means聚类算法把相似状态的交通速度聚类进行建模分析，放大数据的局部特征，更准确地把握交通速度的变化趋势。综合考虑模型的预测精度与计算时间复杂度，使模型具有更高的解释性，选择偏最小二乘回归模型作为最终的预测模型。

1 研究方法

1.1 路网时空相关性的挖掘

为分析相关路段交通流对目标路段交通流的影响程度，估计交通流之间的相关性，而不是直接对交通流本身进行聚类。若城市道路网络中某一区域内含有P节路段，且每一路段上都装有环路检测器（传感器）以采集实时的交通速度数据，可以得到P条路段的历史交通速度数据所组成的时间序列数据V=（V1，V2，…，VP），

2 实证分析

2.1 研究区域概况

为验证提出模型的有效性，选取青岛市西海岸新区长江中路作为主要的研究区域。青岛市西海岸新区长江路是一条东西走向的主干道，沿线串联了新区的行政、商务、教育、餐饮、居住功能区，路口较多，交通流密集，尤其是上下班的早晚高峰时段，人车交织，导致通车效率不高、交通事故频发，长江中路路段尤为严重。作为新区核心位置的主干道，长江中路的交通服务品质难以满足日益增长的社会需求，成为新区主要的道路“瓶颈”。

将青岛市西海岸新区长江中路作为目标道路，为清晰、直观地观察各条路段的地理位置，从OpenStreetMap官网下载路网矢量数据，如图1所示。研究地点具有典型拓扑结构，展示了交通流之间不同程度的时空相关性，这七条道路虽位于不同的方向，但间接相连，每条道路对应不同的道路名称，具体对应关系见表1。

2.2 数据预处理

研究数据为青岛市西海岸新区长江中路2017年8月7日至2017年8月20日出租车GPS轨迹数据，利用Python软件对其预处理，获得有效数据1 752 694条，出租车GPS原始轨迹数据示例见表2。

其中，v（k）为当前路段在时间间隔k内的平均速度，vi，n为第n辆出租车在第i个GPS点处的速度值，i为当前路段内GPS点的编号，I为当前路段内所有GPS点的数量，n是当前路段内出租车的编号，N为当前路段上所有出租车的数量，Nk是时间间隔k内经过当前路段的车辆数。

为了解西海岸新区长江中路交通速度的宏观特征，基于预处理后的数据，利用Python软件绘制2017年8月7日至8月20日交通速度热力图（图2），交通速度存在明显的周期性和日相似特征，即不同天的同一时间段的速度值有着相类似的趋势规律，而同一天的不同时间段存在着较大的差异。图2中颜色的深浅代表了交通速度值的大小，颜色越深，速度就越小，代表道路越拥堵，长江中路8月7日至8月20日的交通流速度数据存在明显的双峰现象，且出行的早高峰集中于07∶00～08∶30时间段，晚高峰集中17∶00～19∶00时间段。

2.3 构建时空相关矩阵

根据长江中路早晚高峰时段的分布状况，利用式（2）分别计算长江中路2017年8月19日8∶30的早高峰时空相关矩阵与2017年8月19日19∶00的晚高峰时空相关矩阵，时间延迟d分别设置为18与24个时间间隔，每个时间间隔为5 min，相应的时空相关矩阵热力图如图3所示。

图中颜色的深浅代表了目标路段R3的交通速度与其他路段交通速度之间相关性的大小，颜色越深代表相关性越强。结果分析发现，早高峰时段，当时间延迟为0时，路段R3与路段R1、路段R4、路段R5以及路段R7的相关系数均为正值，且大于0.5。晚高峰时段，在时间延迟为0时，路段R3与路段R1、路段R2以及路段R4（相关系数的绝对值大于0.5。7条路段在不同时间延迟下相关系数的变化趋势相似，但在同一时间延迟下路段之间交通速度的相关性强度有较大差异。这说明选择的路段之间存在较强的相关性，可以通过时空相关矩阵的聚类来捕获交通流之间的时空相关的异质性。

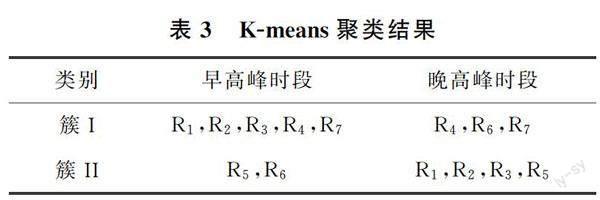
2.4 K-means聚类结果

为了确定聚类数目m值，采用方差比准则（Calinski-Harabaz Index，CHI）评价聚类效果，CHI基于数据集特性评估聚类效果，值越大代表聚类的效果越好［16］。CHI值随m值的变化趋势如图4所示。可知，m=2时CHI值取得最大值，说明两种情况均在划分为两簇时聚类效果最佳，因此将训练数据集分为两簇。

K-means聚类结果见表3。可以看出，早、晚高峰时段的数据虽均被划分为两簇，但两簇之间并不完全相同。如路段R1、R3始终在同一簇中，说明路段R3与路段R1的交通状态最为相似；而路段R6缺少办公楼、商场、医院等因素吸引人车流入，始终在数量少的一簇内。在不同的高峰时段，路段R4与路段R5被划分到了不同的簇中，这可能与路段所处的地理位置、交通流流向以及周边的兴趣点（Point of Interest，POI）属性相关。路段R4为城市主干道，西邻富春江路小学，东邻青岛西海岸新区中心医院，早高峰时段与相邻路段的车流来往密切，而路段R5穿过居民区，在晚高峰时段与相邻路段的车流关系密切，说明同一天不同时间段的交通速度之间存在差异性。

2.5 基于偏最小二乘算法的短时交通速度预测

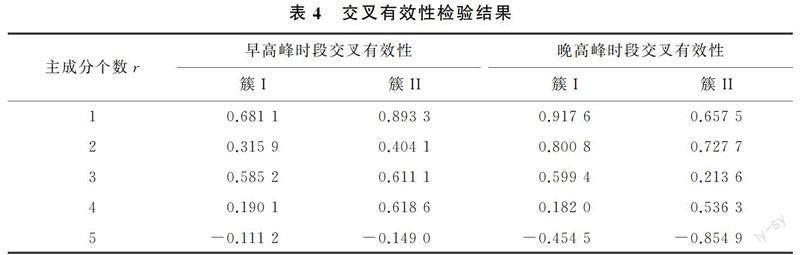
利用K-means聚类算法得到与目标路段R3在早晚高峰时段最相关的路段，筛选出与目标路段的交通速度具有高相关性的历史数据集，使用更新后的数据集构建基于偏最小二乘算法的短时交通速度预测模型。由偏最小二乘算法的建模过程可知，只需选取前r个主成分建立回归方程就可以达到较好的预测精度，r个成分的选择提取可通过进行交叉有效性检验来确认［20］。交叉有效性检验结果见表4。

由表4可知，前4个主成分的交叉有效性均大于0.097 5，但第5个主成分交叉有效性小于0.097 5，不满足交叉有效性提取条件，表明该成分不能明显改善模型的拟合能力，因此，模型只提取前4个主成分，得到标准化偏最小二乘回归方程为

其中，y*zao、y*wan分别为长江中路在早高峰时段和晚高峰时段的预测模型。最终预测的效果如图5所示。

对比图5（a）与（b），早高峰时段交通速度的预测值更接近于真实值，晚高峰时段的预测值误差略大，说明该模型对高频率波动的数据预测精度相对较差，但预测值与真实值的总体变化趋势是一致的。长江中路交通速度整体较为平缓，早高峰时段集中在15～25 km/h，晚高峰时段集中在10～20 km/h，晚高峰速度值低于早高峰，因为长江中路位于经济开发区中心，商场较多，晚间时段人口集中，车流密度大。

2.6 模型评价

其中，yi为交通速度的真实值；i为模型预测值；N为测试样本集的个数。对比结果见表5、表6。

添加“周”周期并采取对历史数据集先聚类后预测的方法，模型的预测精度有了较明显的改善。与经典模型相比，本文提出的基于K-means聚类与PLS回归预测模型的预测精度最佳。这说明通过构建时空相关矩阵并对其进行聚类，筛选出与目标路段相关性最强的路段，更新训练数据集，可以提高模型的预测精度。相比于LSTM模型，PLS回归模型具有更高的预测精度，且模型的训练时间更少。这说明PLS回归模型不仅能够以量化的方式给出模型提高精度过程，具有更强的解释性，且模型的计算复杂度更低。

3 结论

本文的交通速度短时预测模型通过计算时空相关矩阵挖掘路网中相邻路段之间交通速度的关联性，利用K-means聚类更新数据集，结合PLS回归模型预测交通速度。本文模型相比于传统方法具有更高的预测精度，模型的预测速度和可解释性也有较大的提升，是一种可行的交通速度短时预测方法。后续研究中，将考虑组合模型的方式，在模型训练过程中选择添加其他时段的交通速度数据，以增强模型的适用性。

参考文献

［1］VLAHOGIANNI E I， KARLAFTIS M G， GOLIAS J C. Short-term traffic forecasting： Where we are and where we′re going［J］. Transportation Research Part C-Emerging Technologies， 2014， 43（1）： 3-19.

［2］袁健， 范炳全. 交通流短時预测研究进展［J］. 城市交通， 2012，10（6）：73-79.

［3］周辉宇， 李瑞敏， 黄安强， 等. 基于时空关联规则挖掘的城市交通拥堵传导预测［J］. 系统工程理论与实践，2022， 42（8）： 2210-2224.

［4］张国赟， 金辉. 基于改进ARIMA模型的城市轨道交通短时客流预测研究［J］. 计算机应用与软件， 2022， 39（1）： 339-344.

［5］LI W， WANG J X， FAN R， et al. Short-term traffic state prediction from latent structures： Accuracy vs. efficiency［J］. Transportation Research Part C-Emerging Technologies， 2020， 111： 72-90.

［6］CHEN R， LIANG C Y， HONG W C， et al. Forecasting holiday daily tourist flow based on seasonal support vector regression with adaptive genetic algorithm［J］. Applied Soft Computing， 2015， 26： 435-443.

［7］LI Y F， JIANG X， ZHU H， et al. Multiple measures-based chaotic time series for traffic flow prediction based on Bayesian theory［J］. Nonlinear Dynamics， 2016， 85（1）：179-194.

［8］PRIAMBODO B， AHMAD A， KADIR R A. Spatio-temporal K-NN prediction of traffic state based on statistical features in neighboring roads［J］. Journal of Intelligent and Fuzzy Systems， 2021， 40（5）： 9059-9072.

［9］RUMELHART D E， HINTON G E， WILLIAMS R J. Learning representations by back-propagating errors［J］. Nature， 1986， 323： 533-536.

［10］  SUN Z Y， HU Y J， LI W， et al. Prediction model for short-term traffic flow based on a K-means-gated recurrent unit combination［J］. IET Intelligent Transport Systems， 2022， 16（5）： 675-690.

［11］ KANG C L， ZHANG Z Y. Application of LSTM in short-term traffic flow prediction［C］// 2020 IEEE 5th International Conference on Intelligent Transportation Engineering （ICITE）. Beijing， 2020： 98-101.

［12］ LI Z Y， GE H X， CHENG R J. Traffic flow prediction based on BILSTM model and data denoising scheme［J］. Chinese Physics B， 2022，31（4）：214-223.

［13］ BRUNA J， ZAREMBA W， SZLAM A， et al. Spectral networks and locally connected networks on graphs［DB/OL］.［2022-08-30］. https：//arxiv.org/pdf/1312.6203.pdf.

［14］ SHEN G J， HAN X， CHIN K， et al. An attention-based digraph convolution network enabled framework for congestion recognition in three-dimensional road networks［J］. IEEE Transactions on Intelligent Transportation Systems， 2021，23（9）： 14413-14426.

［15］ CHENG Z Y， WANG W， LU J， et al. Classifying the traffic state of urban expressways： A machine-learning approach［J］. Transportation Research Part A-Policy and Practice， 2020， 137： 411-428.

［16］ 王旭鵬， 王梦灵. 基于相似性聚类的交通流概率组合预测模型［J］. 华东理工大学学报（自然科学版）， 2022， 48（3）： 381-387.

［17］ ZHANG Z H， WANG Y P， CHEN P， et al. Probe data-driven travel time forecasting for urban expressways by matching similar spatiotemporal traffic patterns［J］. Transportation Research Part C-Emerging Technologies， 2017， 85： 476-493.

［18］ GUO Y N， YANG H， CHEN M Y， et al. Ensemble prediction-based dynamic robust multi-objective optimization methods［J］. Swarm and Evolutionary Computation， 2019， 48： 156-171.

［19］ YANG L K， GUO Y N， CHENG J， et al. Manifold distance-based over-sampling technique for class imbalance learning［C］// 33rd AAAI Conference on Artificial Intelligence/31st Innovative Applications of Artificial Intelligence Conference/ 9th AAAI Symposium on Educational Advances in Artificial Intelligence. Hawaii， 2019： 10071-10072.

［20］ 王德政， 张益农， 杨帆. 基于MapReduce的并行PLS过程监控算法实现［J］. 计算机工程与应用， 2018， 54（24）： 61-65+175.

Short-term Prediction of Traffic Speed Based on K-means Clustering and PLS Regression Model

JIA Xiu-yan， SUN Qiu-xia， LI Qing

（College of Mathematics and Systems Science， Shandong University of Science and Technology， Qingdao 266590， China）

Abstract： To achieve effective extraction of local features of traffic flow and to improve the interpretability of traffic prediction models， a K-means clustering and PLS regression model was proposed to predict short-time traffic speed. The Spatio-temporal correlation matrix was calculated to explore the correlation between the traffic speeds of adjacent road sections in the road network. The K-means clustering algorithm was used to divide the historical data set. The PLS regression model was used to make the predictions. To verify the accuracy of the model for short-time traffic speed prediction， the GPS data of taxis was selected for validation. The experimental results show that the models prediction error is reduced by about 30% compared with the ARIMA， PLS regression， and LSTM models.

Keywords： urban transportation; short-term speed prediction; K-means clustering; partial least squares regression; spatio-temporal correlation matrix

收稿日期：2022-09-09

基金項目：山东省自然科学基金面上项目（批准号：ZR2021MF113）资助。

通信作者：孙秋霞，女，博士，副教授，主要研究方向为交通大数据分析与建模。E-mail：qiuxiasun@sdust.edu.cn。