关于经典高斯和及其一个新的恒等式

张文鹏,高洁洁

(西北大学 数学学院,陕西 西安 710127)

设q为整数,χ表示模q的Dirichlet特征,对任意整数m,经典高斯和G(m,χ;q)定义为:

其中e(y)=e2πiy,i2=-1。

设p为奇素数且p≡1 mod 3,λ是模p的任意3阶特征,则有恒等式

(1)

Chen Z Y等[6]研究了4阶特征所对应的高斯和性质,并证明了如下结论。

对任意素数p满足p≡1 mod 4,有恒等式

(2)

这里值得指出的是在式(2)中常数α(p)有着特殊的意义。事实上当p≡1 mod 4时,一定可以表示成两个非零整数的平方和。即(参阅文献[3]中定理4-11)

p=α2(p)+β2(p)=

其中r是模p的任意二次非剩余。

Chen L[7]对模p的6阶原特征的情况进行了讨论,并证明了对任意素数p≡1 mod 6以及6阶原特征ψmodp,有恒等式

式中i2=-1,d与式(1)中的定义相同。

纵观以上几个高斯和的结果,其特点是这些原特征的个数均为2,即欧拉函数φ(4)=φ(3)=φ(6)=2。最近,Zhang W P等[8]研究了12阶特征的情况,证明了对任意素数p≡1 mod 12及12阶原特征χ12modp,有

(d2-2p)·(4α2(p)-3p),

(3)

其中d和α(p)的定义与式(1)与式(2)中相同。

由式(3)立刻推出恒等式

(4α2(p)-3p)|。

因为φ(12)=4且当p≡1 mod 8时,模p的8阶原特征的个数也是4,即欧拉函数φ(8)=4。所以我们自然会想到,对应的高斯和是否也存在一个类似于式(3)的恒等式,本文的主要目的就是研究这一问题,并利用初等方法以及经典高斯和的性质证明下面的结果。

定理1设p是一个奇素数且p≡1 mod 8,那么对模p的任意8阶特征χ8,有恒等式

注释本文中的定理虽然给出了8阶特征高斯和的计算公式,但是其结论也有缺陷性,即表达式中含有多项式的二次特征和不能计算出具体值。对于其中包含的二次特征和,是否能计算出它的精确值是一个有趣的公开问题!

此外,注意到φ(5)=4,所以当p≡1 mod 5时,模p的5阶原特征个数也是4。对于5阶特征以及2h阶特征(h≥4)对应的高斯和,是否也有一个类似于我们定理的计算公式,它是一个有意义的研究课题。建议有兴趣的读者与我们一起考虑!

1 若干引理

为了完成定理的证明,需要以下引理。在下文中,将用到初等数论知识以及高斯和性质,这些内容在文献[1-3]中有详细的描述,这里不在赘述。

引理1设p是一个奇素数,χ为模p的任意非主特征,则有恒等式

τ(χ)·τ(χχ2)

证明事实上这一结论的一般情况可参阅文献[15],这里给出这一特殊情况的简单证明。

对模p的任一非主特征,由经典高斯和的性质,有

(4)

另一方面,对任意整数b且(b,p)=1,由恒等式

χ2(b)·τ(χ2),

也有

(5)

结合式(4)和(5),有恒等式

(6)

τ(χ2)·τ(χ)·(χχ2)。

于是证明了引理1。

引理2设p是一个奇素数且p≡1 mod 8,χ8为模p的8阶原特征,则有恒等式

(7)

类似也有

(8)

或者

于是证明了引理2。

引理3设p是一个奇素数且p≡1 mod 8,则有恒等式

证明由勒让德符号的性质可得

(9)

应用高斯和的性质,有

(10)

同理可得

(11)

结合式(9),(10)及(11),可得

2χ4(2)·χ8(-1)·

于是证明了引理3。

2 定理的证明

(12)

由式(12)及引理3立刻推出

于是完成了定理1的证明。

3 结语

本文主要利用经典高斯和的性质研究了一类特殊高斯和方幂和的计算问题,并给出了它们的一个精确计算公式。即证明了如下结论:设p为素数满足p≡1 mod 8,χ8为模p的任意8阶特征,那么有恒等式

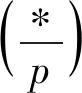
显然这一研究结果是有意义的,它不仅扩充了经典高斯和的研究内容,而且有助于有关方面研究工作的进一步展开!