基于空间重构相干声源的麦克风阵列性能评价技术研究

唐 俊，孙鑫淼，李佳勇，闫 磊

基于空间重构相干声源的麦克风阵列性能评价技术研究

唐 俊1, 2，孙鑫淼1, 2，李佳勇1, 2，闫 磊3

(1. 天津大学建筑工程学院，天津 300350；2. 天津大学天津市港口与海洋工程重点实验室，天津 300350；3. 北京航天计量测试技术研究所，北京 100076)

基于波束形成算法的麦克风阵列系统被广泛应用于噪声源定位中，空间分辨率、动态范围是阵列进行多声源定位中的关键性能参数．工程中常用的阵列性能评估方法为小尺寸声源测试法，受声源尺寸及指向性的影响，其在使用不同声源对同一阵列进行测试时，测试结果往往有较大误差，且该测试方法对环境要求较高．基于此，本文提出了一种基于多通道标准耦合腔声源的空间声源重构方法，可重构出任意位置、频率及强度的空间点声源，通过标准耦合腔输出至对应坐标的麦克风传感器，重构两个相干点声源可代替实际空间小尺度声源对麦克风阵列性能参数进行测量分析．本文选取工程中常用的30通道螺旋形麦克风阵列，分别进行数值模拟、标准耦合腔实验及实际小尺寸声源对比实验．在2～4kHz频段内，多通道耦合腔标准相干声源对阵列的测试结果与数值模拟结果高度一致，表明该方法的有效性．实际小尺寸声源的对比实验结果表明：耦合腔标准声源重构法受测试环境影响程度更低，分析麦克风阵列性能时测量误差小、精度高．

麦克风阵列；声源重构；空间分辨率；动态范围；波束形成

近年来，随着声源定位算法的发展和传感器精度的提高，基于麦克风阵列的声源定位技术在机械噪声测量[1-2]、飞跃噪声测试[3-4]、小型无人机定位[5]等领域有着十分广泛的应用．根据不同的定位原理，其主要分为广义互相关延时估计法[6]、高分辨空间谱估计法[7-8]以及波束形成(beamforming)算法．由于波束形成[9-13]算法具有速度快、精准度高、鲁棒性好等优点，其对稳态和瞬态声源均有良好的识别性能，因此被广泛应用于麦克风阵列定位系统．

波束形成算法是通过对信号进行三维空域加权处理从而实现对信号源定位的一种方法．其性能主要体现在空间分辨率和实际动态范围两方面，该性能直接决定了阵列的多声源识别能力，因此麦克风阵列系统性能参数定量研究对实际应用中的阵列选型具有重要的指导意义．国内外学者从不同方面进行了相关研究．Mukwevho等[14]设计了一维全向线性阵列结构，并评估了该结构下不同波束形成算法的声源识别性能．Cigada等[15]指出了波束形成算法的关键参数，并分析了不同参数对阵列最大可分辨率、空间分辨率和噪声抑制水平的影响．褚志刚等[16-18]以多通道、传感器等距分布的球形阵列为例，通过仿真分析了阵列直径对分辨性能和旁瓣抑制性能的影响. Son[19]提出了一种基于重构声源的不规则阵列插值方法，使稀疏阵列具备与密集阵列相同的阵列波束形成性能．

以往的研究大多通过数值模拟方式评估指定结构下阵列关键性能参数．在实际应用中，由于阵列定位系统的影响(如阵列加工精度、传感器的幅相误差、数据采集设备误差等因素)，关键性能参数均会受到不同程度的影响，导致性能参数偏离理论值，从而造成测量误差．Prasad[20]提出了使用点声源的测试方法，即使用两个尺寸小、空间指向性强的扬声器来近似点声源，并将其应用于航空测量领域. Aldeman[21]提出了一种新型混合螺旋阵型，并基于实际小尺寸扬声器对该阵型完成了一系列角分辨率性能测试，在保证了阵列高分辨性能的同时减小了阵列尺寸．该方法对扬声器尺寸、指向性及测试环境要求较高．目前针对不同阵列定位系统的空间分辨率、动态范围等关键性能参数如何定量分析以及测量结果如何精确溯源等重要问题，尚缺少一种能同时保证工程实施性和精度的评估测试方法．

为解决上述问题，本文提出了一种空间标准相干声源重构方法，基于多通道耦合腔声源搭建了高精度的空间相干多声源重构系统．在阵型选取方面，常见的阵型主要有均匀圆阵、正多边形平面阵以及螺旋阵列[21]．均匀阵列构建简单，但典型问题是鬼影较多．与均匀阵列和正多边形阵列相比，螺旋阵列各频率分辨率接近，鬼影少，各方面指标较好，适用于各种场景，因此被广泛应用于工业噪声定位中．常用的通道数量主要有30、64等，通道数量的增加不会影响该阵型的本质性能，因此本文以工业中常见30通道螺旋形麦克风阵列为研究对象，对麦克风阵列的阵列分辨率及动态范围这两个关键性能参数分别进行数值模拟和试验研究．数值模拟与重构相干声源测试结果的高度一致性验证了本文提出的多通道耦合腔标准相干声源重构方法的有效性，与实际小尺度声源的测试结果对比进一步展示了该方法在减小测量误差、适应测试环境等方面的优势．空间标准相干声源重构方法可有效精确评估麦克风阵列性能，具备良好工程实施性．

1 相干声源重构算法与重构系统

1.1 标准相干声源重构算法

在使用小声源对阵列性能进行实际测试中，阵列平面与声源平面的距离有限，符合近场模型[22]，声源的辐射声波更接近球面波，不同位置传感器接收到的声压信号幅值和相位均存在一定的差异，如图1所示.

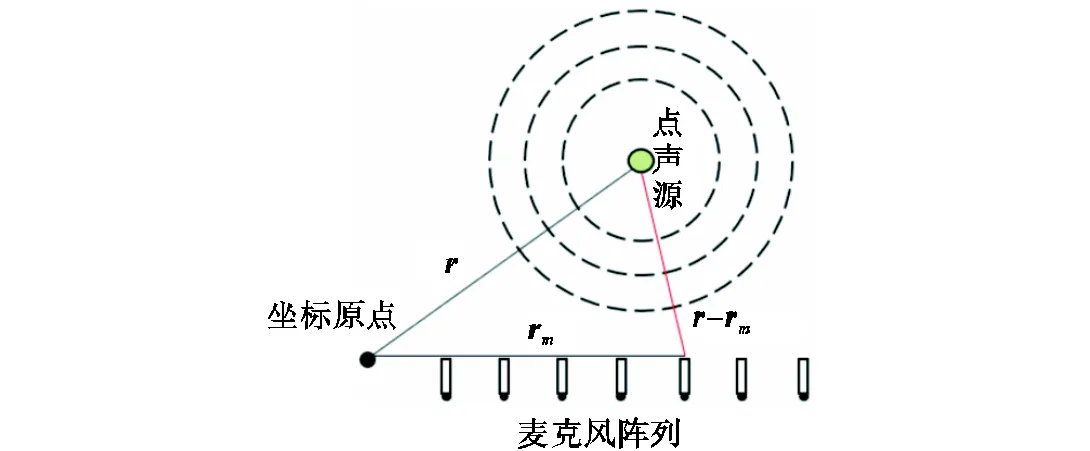
图1 点声源辐射声场[22]

假设单极子点声源位于声源计算平面上位置，0为声源信号，无反射的自由声场中的格林函数为

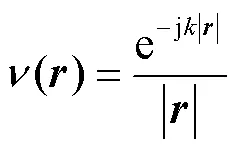
式中为波数．

则各传声器接收的声压信号为

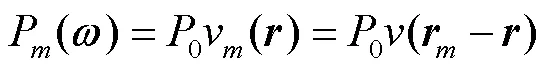
当有空间有多个点声源时，阵列各传声器接收的声压信号为空间各点声源的叠加[23]，即

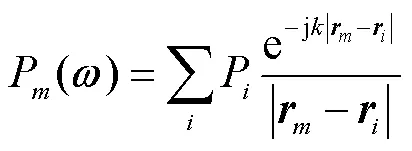
式中P是位于处的第个点声源信号．

如图2所示，用螺旋形麦克风阵列作为阵型，以阵列中心为空间坐标原点，阵列直径为，声源到阵列面的垂直距离为0，声源位于处，号麦克风传感器位于处．

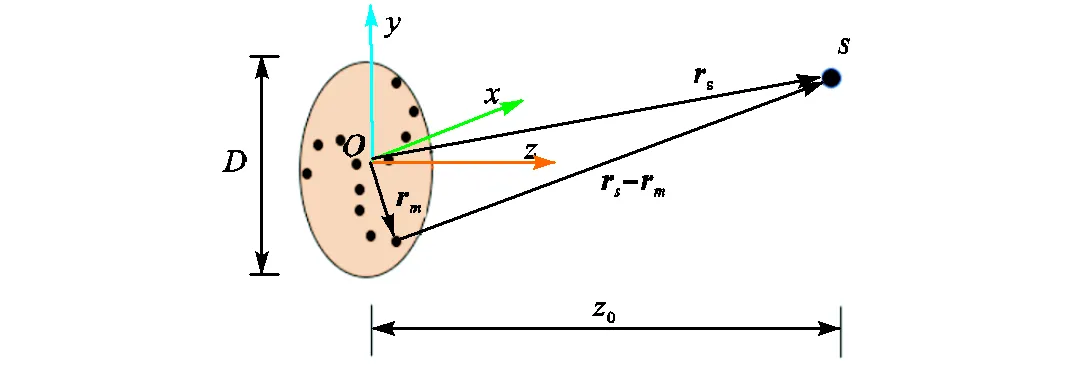
图2 阵列模式示意

假设声源数量为，麦克风数量为，声源(＝1，2，…，)相对号麦克风(＝1，2，…，)的转向矢量可表示为

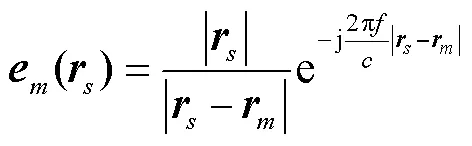
假设声源强度为q，号麦克风传感器接收到的声压信号p可表示为

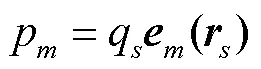
推广至多声源，式(5)可写成矩阵形式为

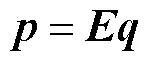
式中：为麦克风阵列接收到的声压信号，∈R×1；为转向矢量矩阵，∈R×；为声源强度，∈ R×1.

1.2 标准相干声源重构系统

由相干声源重构算法可根据多声源与阵列传感器的相对位置关系计算出每个传感器接收到的标准相干声压信号，并通过标准耦合腔声源将该声压输出至待测试阵列，其结果相当于空间中真实存在多个点声源时阵列传感器接收到的动态声压信号．

相干声源重构系统由上位机(编号①)、多通道信号输出卡(编号②)、耦合腔标准声源(编号③)、待测试阵列系统(编号④)、数据采集装置(编号⑤)和声源定位下位机(编号⑥)组成，如图3所示．阵列固定后，以阵列平面中心为空间坐标原点，传感器空间坐标位置唯一．通过第1.1节物理模型可重构空间存在多个声源时各个传感器接收到的动态声压信号，上位机程序将计算好的电信号输出至对应的耦合腔标准声源，通过耦合腔实现电声转换，并将动态声压信号输送至麦克风阵列各传感器．由于耦合腔腔体的密闭环境，降低了测试的环境要求，同时通道之间互不干扰．

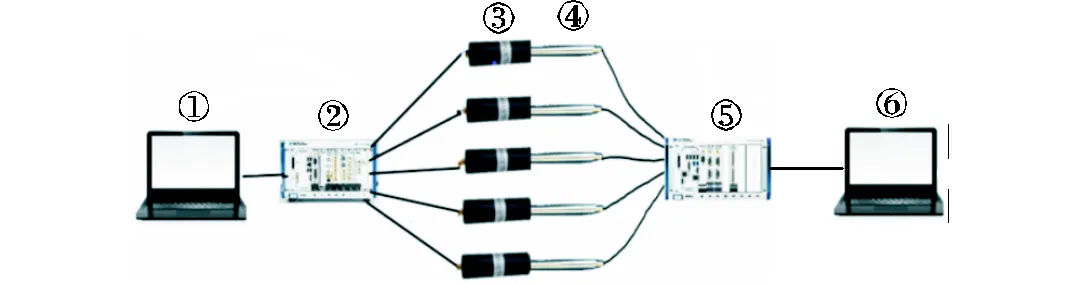
图3 相干声源重构系统示意

系统中的耦合腔标准声源采用活塞式声发射面板，通过耦合腔设计将标准声源和传声器连接，传声器插入腔体后使用带密封圈的紧固螺栓固定，保证耦合腔内是一个封闭的空间，从而组成了一个耦合腔标准声源，该声源可按照预设值发出所需的声信号．

为保证输出信号的幅相精度，在100～4000Hz频段内对标准耦合腔声源进行幅相特性分析，建立误差修正系数．幅相误差分析过程如图4所示：将信号源1()分为两路，上支直接输送至幅误差分析模块，下支驱动耦合腔标准声源发声，使用B&K 4938传感器作为参考麦克风得到声信号2()输送至误差分析模块，系统中2()相对信号源1()产生的幅相误差仅来自于耦合腔标准声源．

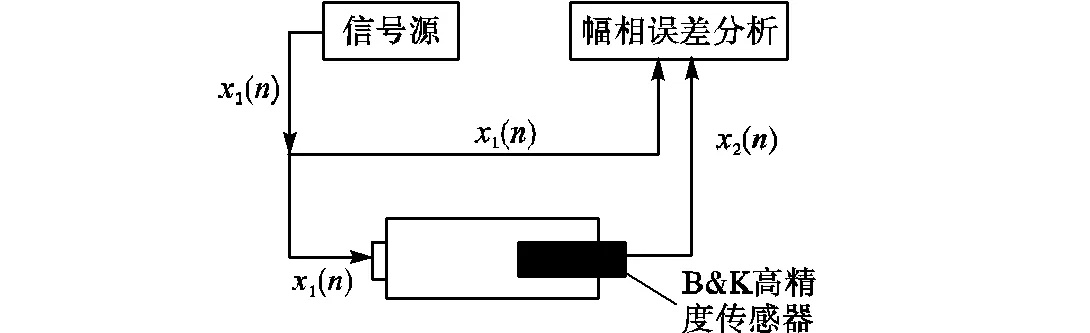
图4 耦合腔声源幅相误差分析[22]

本文使用了30个耦合腔标准声源构建了多通道相干声源重构系统，30通道耦合腔声源幅相误差分析如图5所示．如图5(a)所示，耦合腔声源在不同频率下的最大平均振幅为1.023V，最小为0.908V．不同频率下平均振幅的标准偏差为0.03，显示了耦合腔声源的幅频响应具有良好的一致性．从图5(b)可以看出，1()和2()在不同频率下的相位误差约为0.00004°，平均相位差和标准偏差都非常小，声源相位一致性良好．根据多通道耦合腔声源幅相误差分析结果可以建立校正数据库来修改声源的输出以确保其输出信号的同步和准确性．

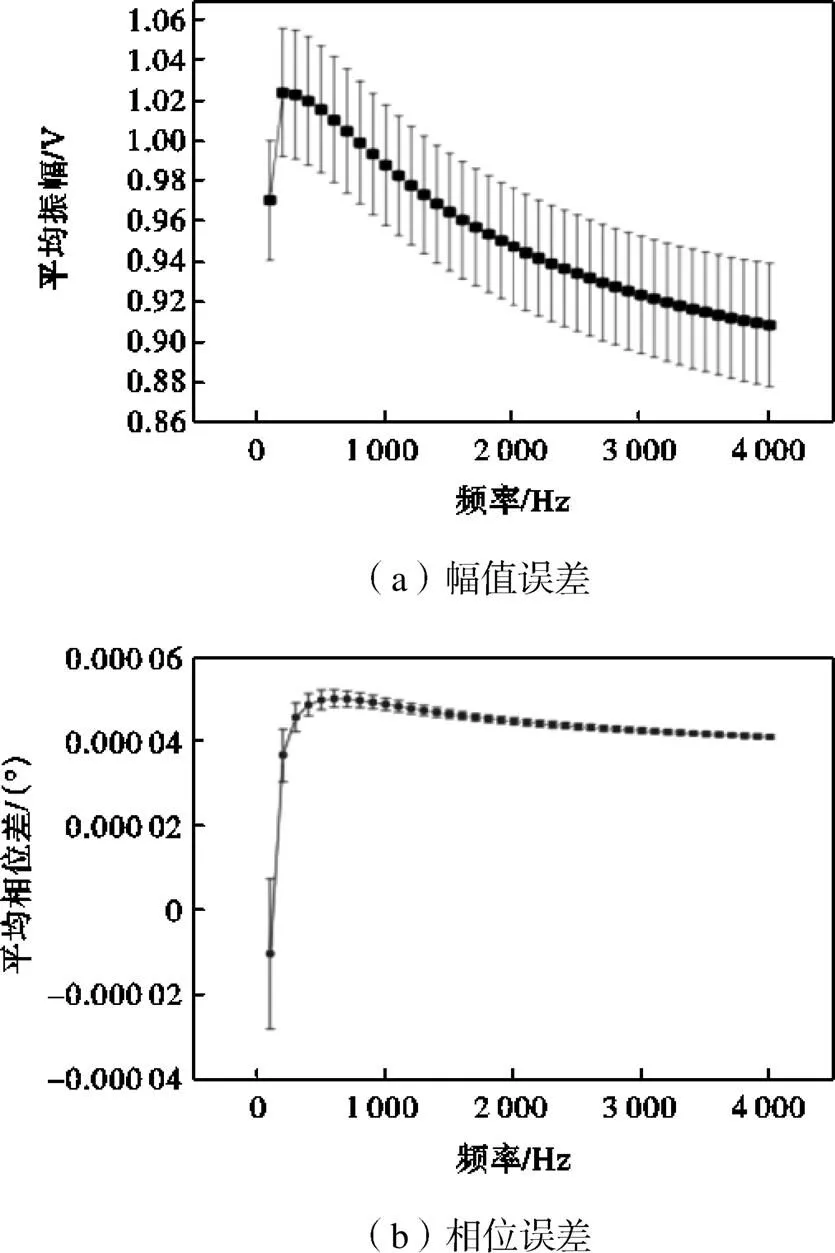
图5 耦合腔声源幅相误差系数曲线

2 麦克风阵列关键性能分析

选择30通道麦克风阵列为研究对象，应用波束形成算法进行空间声源识别定位，对阵列的空间分辨率和动态范围两个关键性能参数开展仿真研究．

2.1 麦克风阵列参数

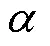
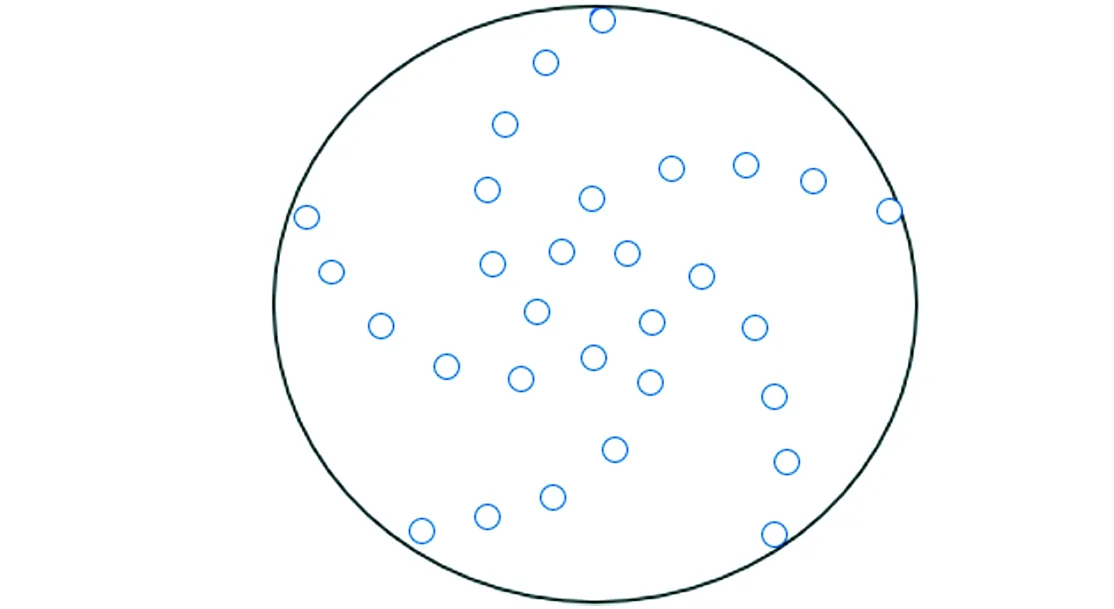
图6 麦克风阵列阵型

表1 阵列模式主要参数

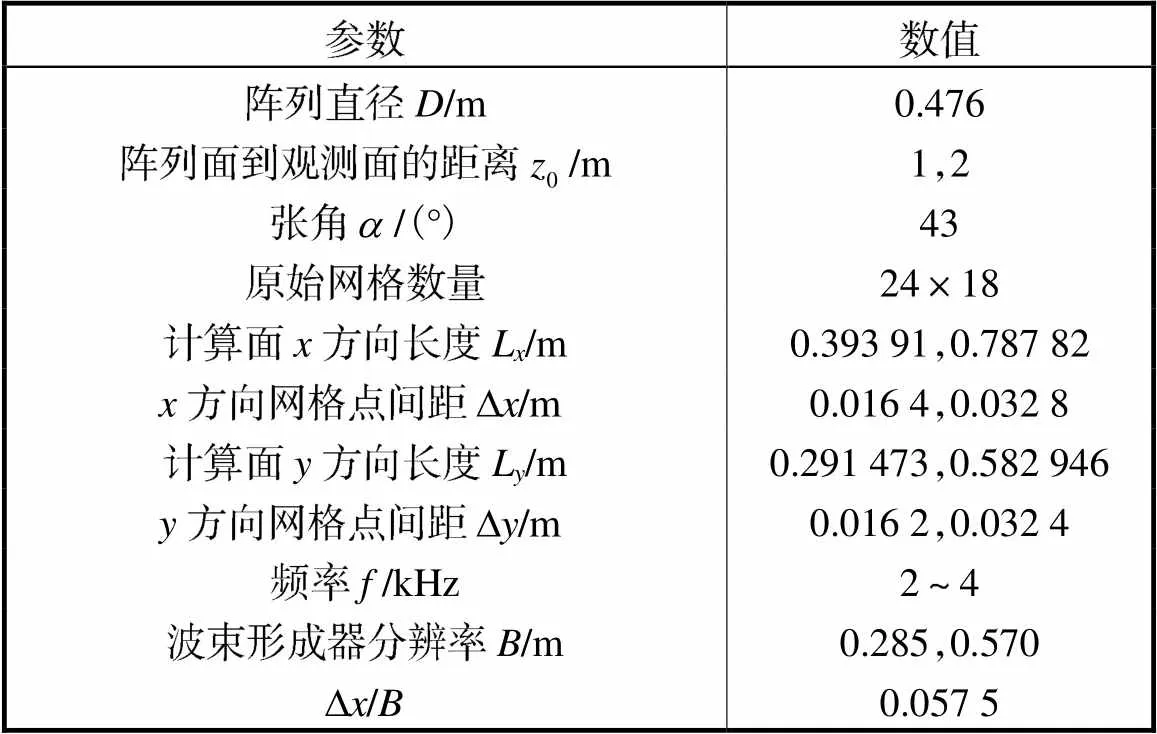
Tab.1 Main parameters of array mode

2.2 空间分辨率

空间分辨率是声源计算平面上能够被准确识别的两同频等强度声源间的最小距离，其反映了阵列对多声源的识别能力，是多声源识别问题中阵列的主要性能参数之一．数学上常用基于瑞利准则的分辨 率[16]定义空间分辨率．瑞利准则为最小可分辨距离(空间分辨率)的常用近似方法，可表示为

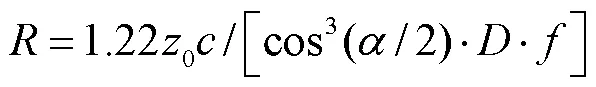
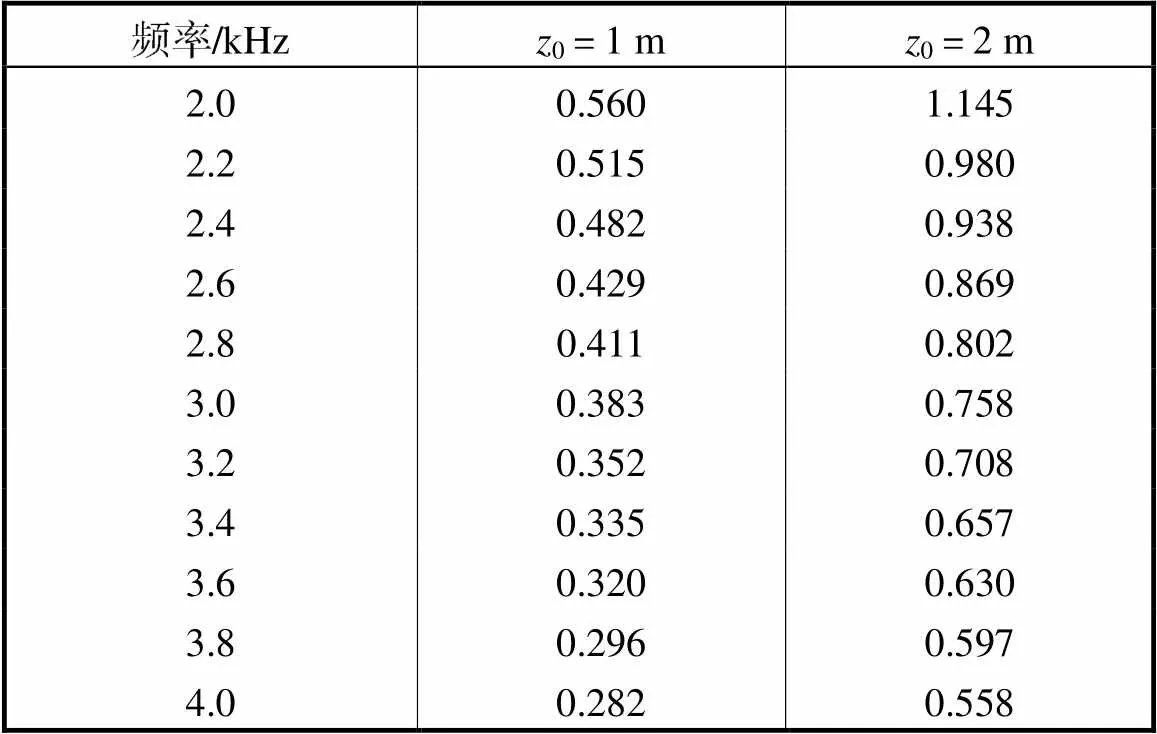
式中为阵列最小可分辨距离．由式(7)可知0、是除阵列固有属性外影响空间分辨率的主要因素，与测试时两声源连线所沿方向(轴、轴和不在、轴上)无关．测试中[21]常通过缩小两声源(固定0下的同一平面内)的间距，直至声源发生混叠，从而确定阵列无法分辨的最小距离，即空间分辨率．因此本文通过缩小位于轴两声源间距，对图6所示阵型的麦克风阵列性能进行数值模拟，使用波束形成算法[26]进行声源识别定位．表2为0分别为1m和2m时阵列空间分辨率测试结果．同时为验证重构算法有效性，使用式(7)估算出的最小可分辨距离进行对比．

表2 单频声源不同距离下的最小分辨距离

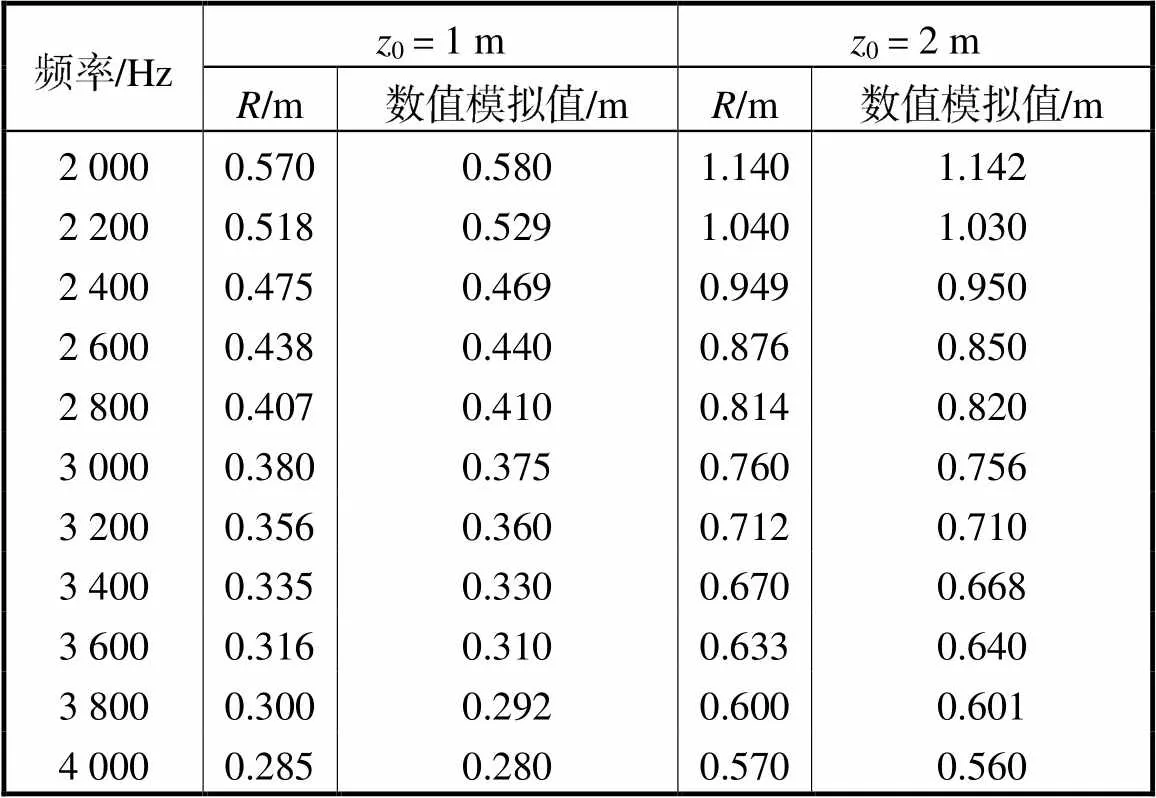
Tab.2 Minimum resolution distance of single-frequency sound source at different distances

设声源间距为，最小可分辨距离为min，图7给出了频率为4kHz、声源距离阵列面为1m时的仿真效果：当＞min时，声压图观测到两主瓣峰值，可清晰分辨；当≈min时，两声源处于可分辨的临界位置；当＜min时，两声源完全发生混叠，仿真结果显示只存在一个扭曲声源，无法清晰分辨．

由表2可知，使用重构算法对阵列进行数值模拟，在距离固定时，声源频率越高，最小可分辨距离越小，空间分辨能力越强；而频率固定时，距离越大，最小可分辨距离越大，空间分辨能力越弱．重构算法评估出的最小可分辨距离与接近．当频率大于3kHz时，数值模拟值与误差约为2～8mm；在频率为2kHz时，误差有所增大，但小于20mm．

2.3 有效动态范围

麦克风阵列的动态范围为主瓣峰与最大旁瓣水平的差值．数学上常用最大旁瓣水平(maximum side lobe，MSL)函数定义，旁瓣是具有多个传感器阵列进行定位时的固有特性[27]．当波束进行空域扫描时，来自非声源位置的波束发生相消干涉，形成旁瓣．来自声源位置的波束发生相长干涉，形成主瓣峰，可通过最大旁瓣水平MSL函数进行表征．式(8)为波束形成算法的权值：

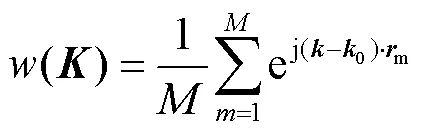
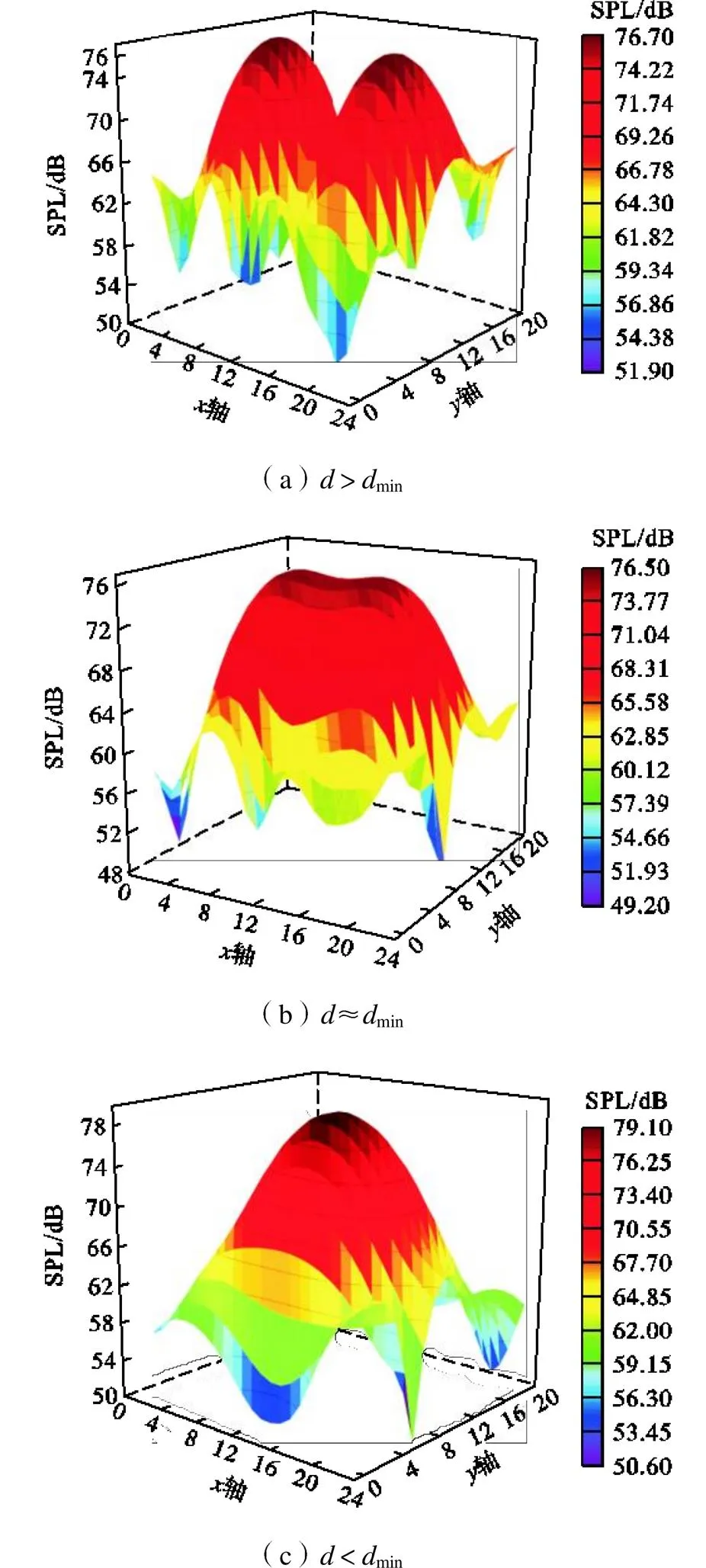
图7 不同声源间距下数值模拟对比

波束形成输出的最大旁瓣相对于主瓣峰值动态范围的高低，反映了其抑制旁瓣干扰的能力．式(9)为阵列径向投影函数定义式，由波束形成权值可得最大旁瓣水平定义，见式(10)．

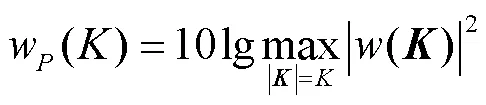
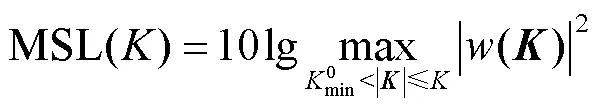
结合式(8)、(10)可以看出，麦克风阵列最大旁瓣水平与频率、阵列阵型、传感器坐标位置均相关，测试中[16]常通过指定声源位置观测其最大旁瓣水平.在实际应用中其定义为两声源的最大可分辨声压级差，通过固定两声源位置并逐渐增大声压级差，当声压级较低的声源被旁瓣掩盖时，该声源所对应的声压级即为最大旁瓣．

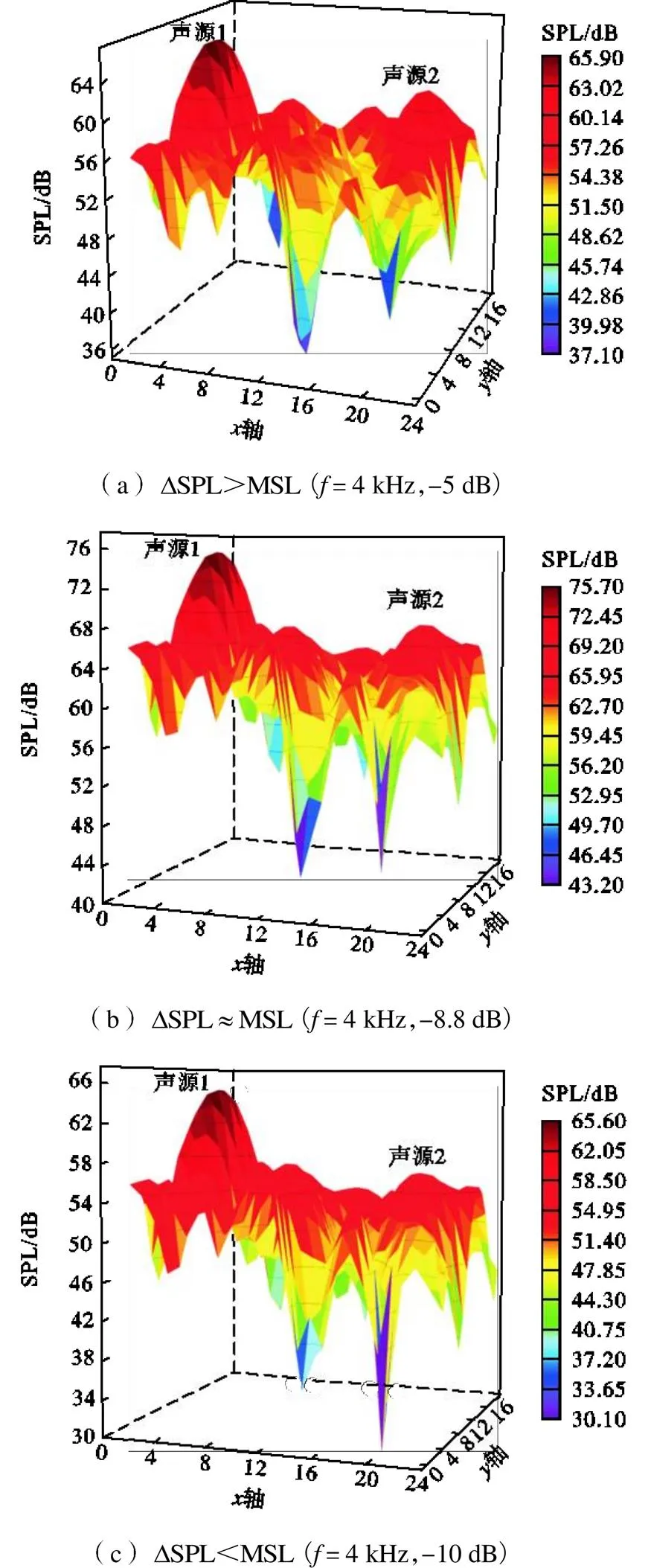
图8 可分辨声压级差

改变声源频率，分别找出不同频率下不能清晰分辨的两声源声压级最大差值，即为待测阵列最大动态范围，结果如表3所示．

表3 数值模拟不同频率下可分辨最大声压级差

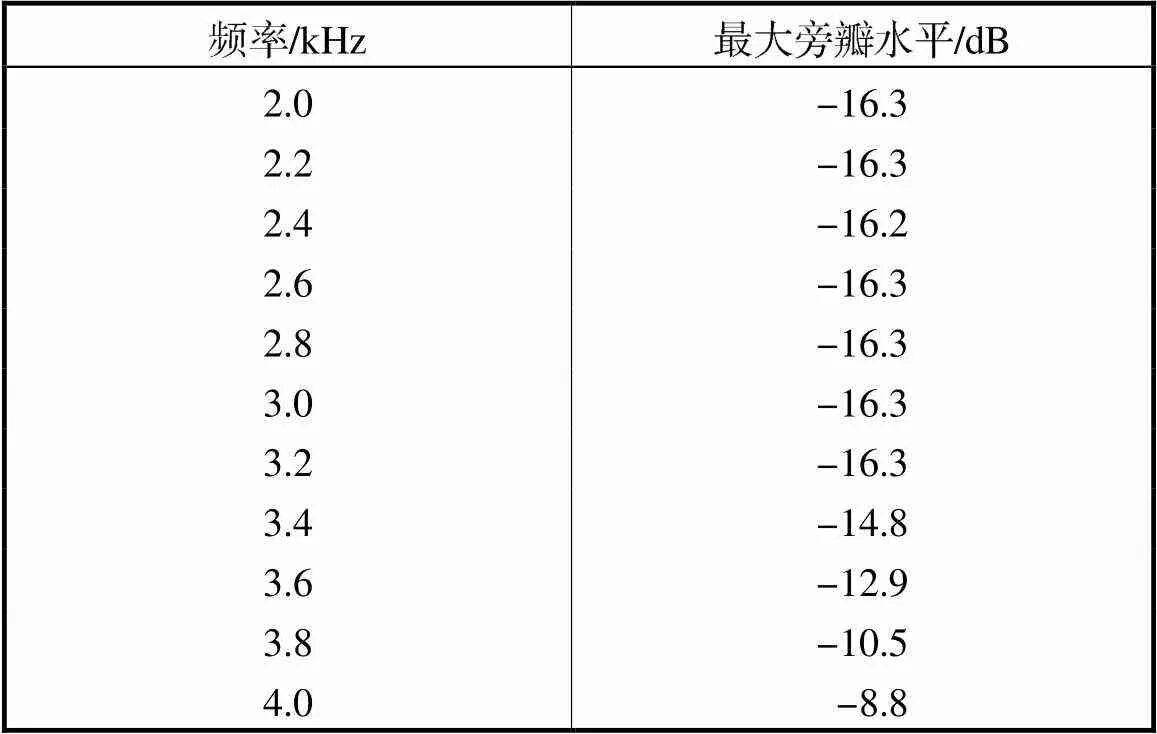
Tab.3 Numerical simulation of maximum distinguishable sound pressure level difference at different fre-quencies

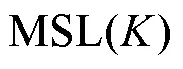
3 麦克风阵列性能测试实验与误差对比分析

搭建标准相干声源重构系统对麦克风阵列性能进行测试，作为比较，搭建一套小尺度声源测试系统对同一个麦克风阵列进行性能测试．

3.1 测试实验系统

实验测试对象为30通道螺旋形麦克风阵列，阵列使用PCB130E22传声器．通过声压图和摄像头视频画面叠加，对声源进行空间可视定位．为保证波束声压图与摄像头采集画面的一致性，摄像头位于阵列几何中心，阵列采样频率为25.6kHz．为保证数据同步采集和接收，使用NI-9264 DA输出卡将重构声源信号输出至耦合腔标准声源，并通过NI-9231采集卡对阵列传感器接收到的时域声压信号进行接收，进一步通过交换机输送至上位机．多通道重构相干声源系统与麦克风阵列的连接如图9所示．

图9 多通道重构相干声源测试系统

3.2 基于耦合腔的标准声源重构实验

基于标准相干声源重构系统，构建空间中的两个标准点声源，分别评估麦克风阵列的空间分辨率和动态范围这两个性能参数．

3.2.1 空间分辨率评估实验

麦克风阵列使用延迟求和波束形成算法对空间声源进行定位成像测量，图10给出了声源频率为4000Hz、声压级为50dB、声源间距变化时的阵列的空间分辨率测试结果．两个声源的初始位置分别位于(0.4m，0m)和(-0.4m，0m)，逐渐缩小两个同频点声源的距离．当两声源坐标分别为(0.2m，0m)和(-0.2m，0m)，即声源间距大于最小识别范围时，声压图可清晰观测两主瓣峰；当两声源坐标分别为(0.14m，0m)和(-0.14m，0m)，即声源间距为0.28m时，处于有效识别区域边缘，重构的声压图出现部分混叠；当声源间距为0.2m时，小于有效识别区域，发生混叠效应，重构的声压图只有一个扭曲的声源，无法有效分辨．由于麦克风阵列测量的声源是系统根据多通道信号构造而成，在空间中并不实际存在，为了更为准确地评估阵列的空间分辨率性能，移除背景图像，便于观测计算平面整体声压级分布．表4给出了2～4kHz频段内被评估的麦克风阵列的最小可分辨距离．

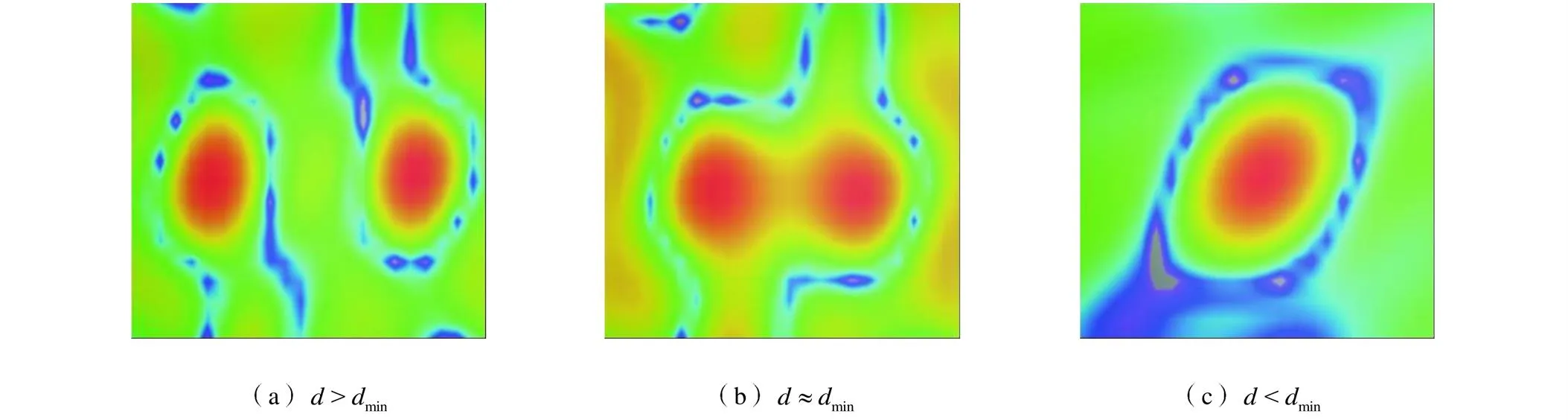
图10 基于耦合腔重构系统的空间分辨率实测结果对比

表4 耦合腔声源重构系统的空间分辨率测试(单位：m)

Tab.4 Spatial resolution measurement of coupled cavity sound source reconstruction system(unit：m)

3.2.2 动态范围评估实验

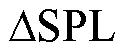
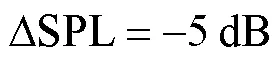
3.3 小尺度声源测试对比实验

为研究耦合腔相干声源重构系统的测量误差，本文设计了如图12所示的小尺寸声源的控制试验台，使用该控制试验台对麦克风阵列进行性能测试．小尺寸声源控制试验台由两台信号发生器、两台前端口径为6mm的声源(内部使用型号为惠威S5N的扬声器)、双通道功率放大器、电动滑台和位移机构组成．试验台通过高精度步进电机控制滑轨调整声源位置，单滑轨长为1m，且最小运动控制精度为1mm.

图11 基于耦合腔重构系统的动态范围实测结果对比

表5 耦合腔声源重构系统的动态范围测试

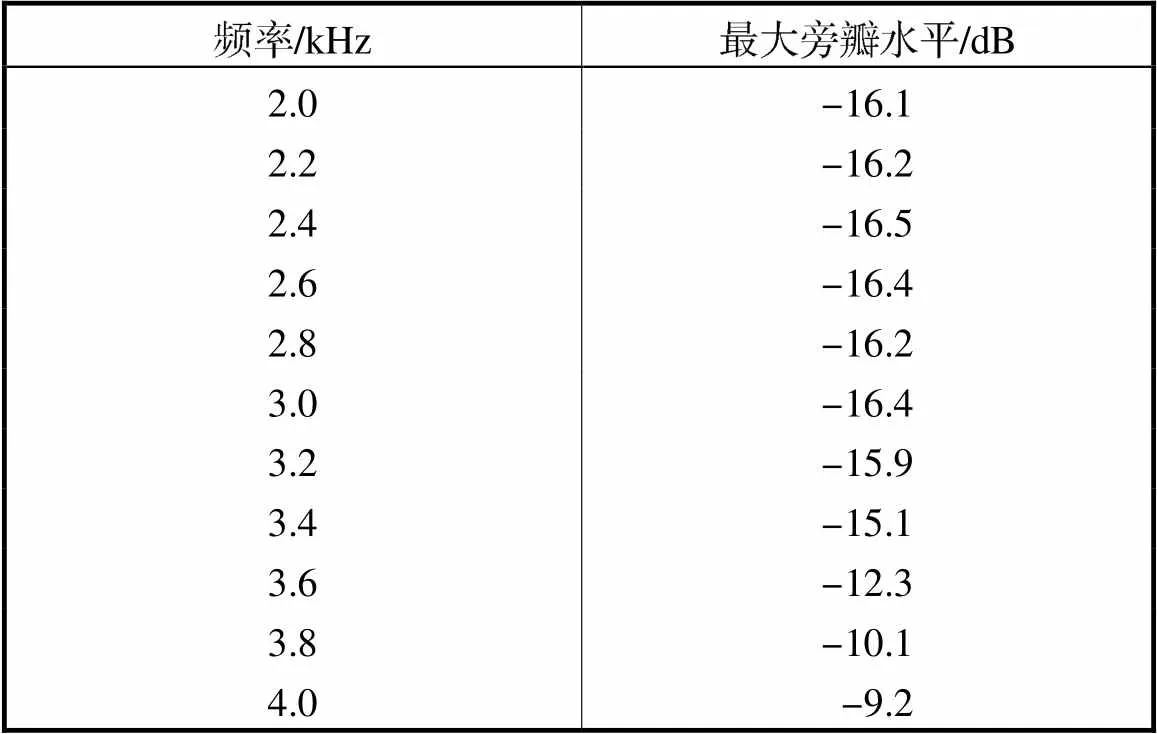
Tab.5 Dynamic range measurement of coupled cavity sound source reconstruction system

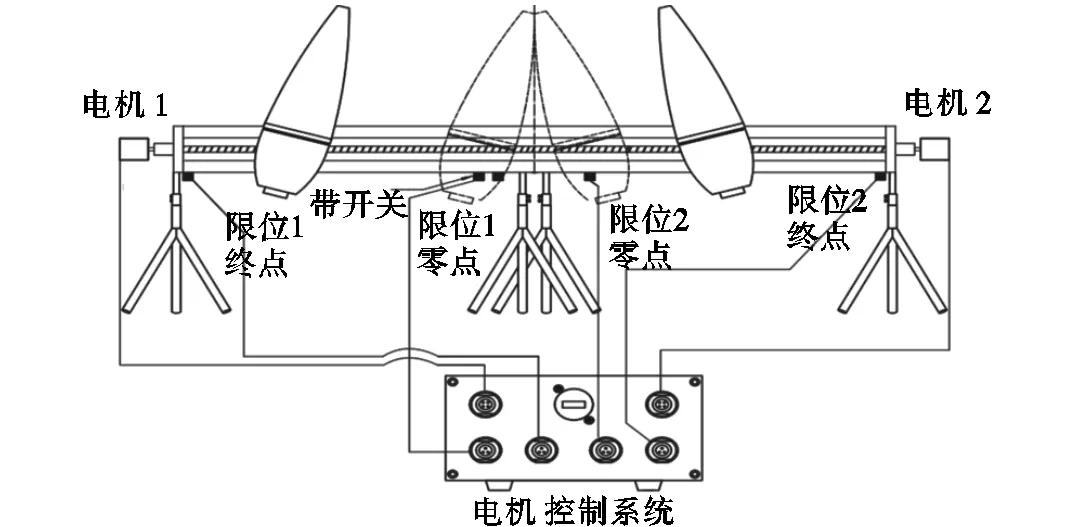
图12 声源控制装置连接示意

无论何种形式的声源，当声波波长远小于声源几何尺寸时，即可视为点声源．但在实际评价中，当声源中心到阵列几何中心的距离超过声源最大几何尺寸的2倍时，可将该声源近似为点声源．本文的小尺寸声源满足上述要求．

在2～4kHz频率范围内由驱动试验台的两个小尺寸声源发声，麦克风阵列对两个声源进行定位成像测量．基于麦克风阵列对声源的成像结果分别评估阵列的空间分辨率和动态范围，实验结果如图13所示.

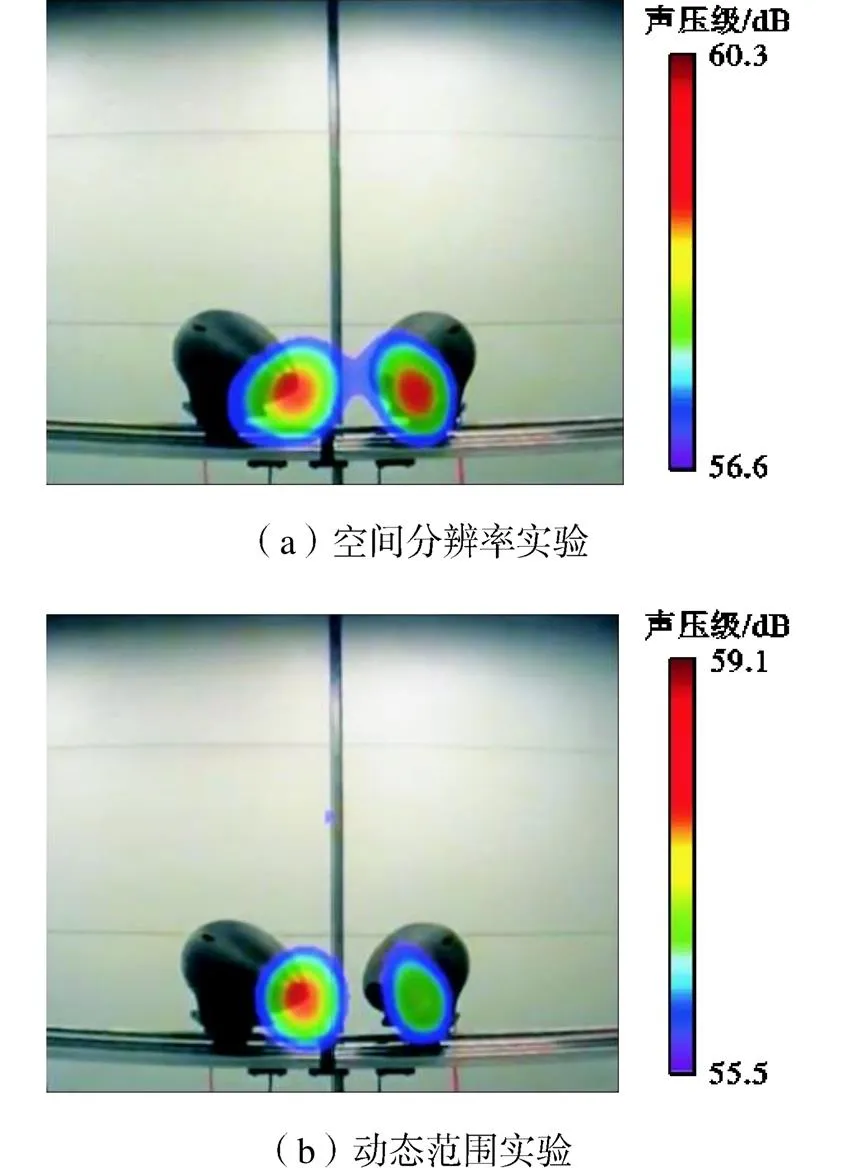
图13 实际小尺寸声源实验

3.4 实验结果分析

本文分别应用标准相干声源重构系统和小尺度声源系统对同一个麦克风阵列进行空间分辨率和动态范围的性能测试，将两种实验系统对麦克风阵列性能的评估结果和数值模拟仿真进行了对比．

图14为声源距离麦克风阵列1m和2m时3种方法得到的麦克风阵列的空间分辨率．整体上，声源到阵列距离0＝2m时，使用3种方法得到的阵列空间最小分辨距离约为0＝1m时的2倍．声源重构系统的测试结果与数值模拟的一致性较好，在较低的2.0～2.5kHz频率范围内，最小空间分辨距离的差值约为1.0cm，而在较高的3.5～4.0kHz频率范围，差值仅为2.0～3.0mm．

使用小尺寸声源测量声阵列的空间分辨率，结果呈现整体偏移的情况，在3.5～4.0kHz频率范围内，测量的最小空间分辨距离的差值约为3.0cm，而在2.0～2.5kHz频率范围内差值达到6.0cm．

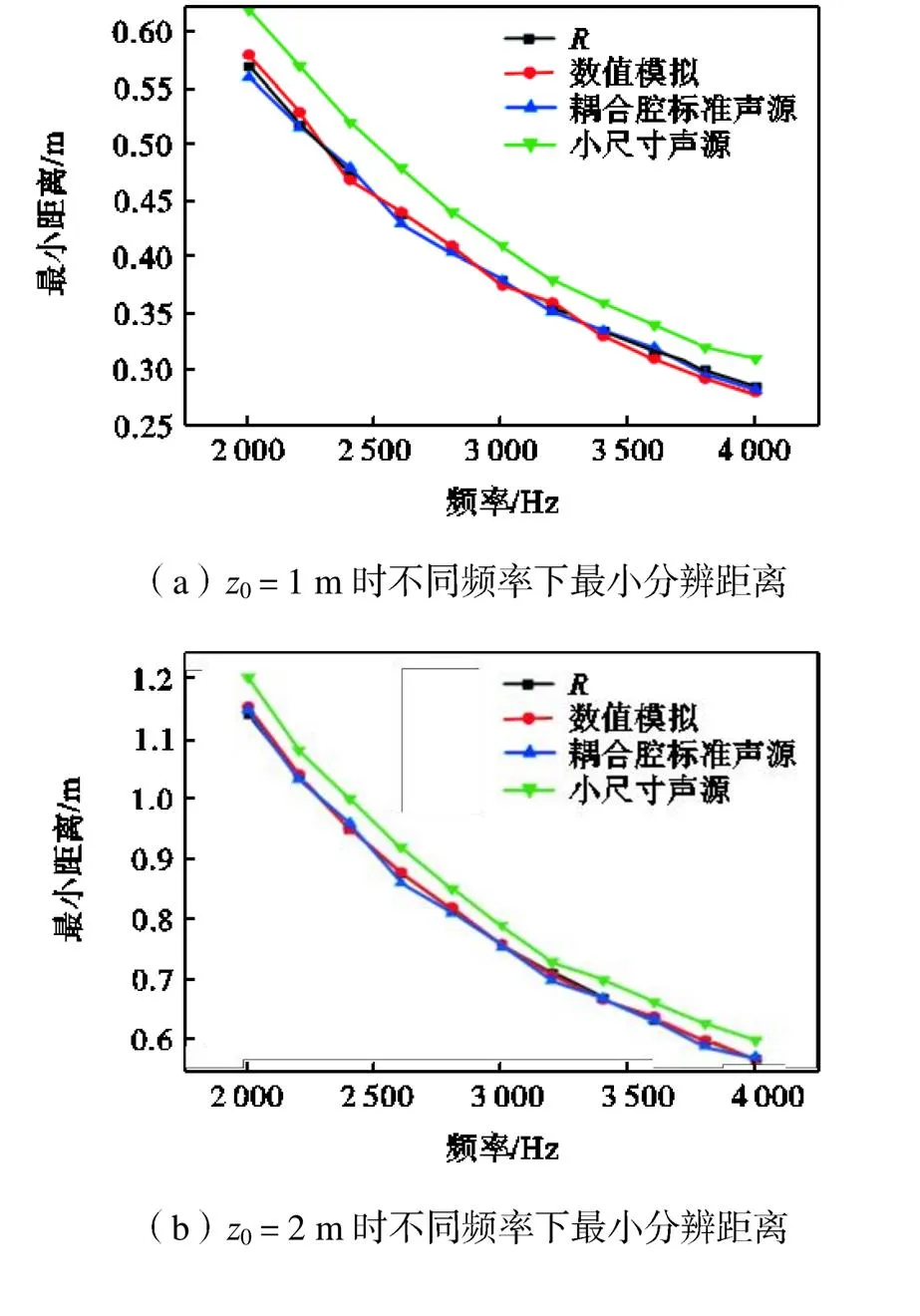
图14 不同距离下的阵列空间分辨率对比

图15为声源距离麦克风阵列1.0m时3种方法得到的麦克风阵列的动态范围．由图15可知，当频率升高时，最大旁瓣水平升高，阵列的有效动态范围变低，声源重构系统的测试结果与数值模拟的一致性较好．

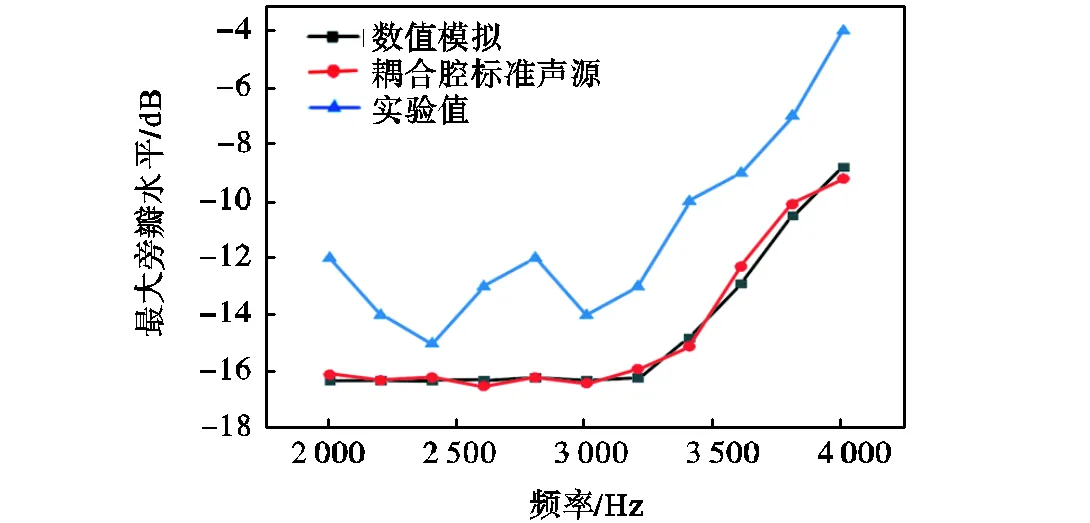
图15 不同频率下的最大旁瓣水平

使用小尺寸声源测量声阵列的动态范围时，由于实验环境并非完全理想，且声源具有一定的尺寸，不能完全视为点声源，测试误差较大，测量得到的最大旁瓣水平比数值模拟结果高约3～4dB．在2～3kHz频段内，最大旁瓣水平在-12～-15dB内波动，相比声源重构系统的测试结果与数值模拟结果，小尺寸声源的测量误差较大．

以上实验对比分析结果表明，基于标准相干声源重构系统对麦克风阵列的性能评估方法优于传统的小尺度声源方法，具有更小的测量误差．

4 结 论

对麦克风阵列声源定位关键性能参数进行评估时，使用小尺寸声源进行测试对实验环境及声源尺寸要求较高，不满足工程应用中精确、高效的测试需要．本文提出了一种基于多声源相干声场的空间标准重构声源测试方法，分别对麦克风阵列的空间分辨率和动态范围这两个关键性能参数进行了实验测量，结果表明该方法是一种较为理想的麦克风阵列性能参数测量手段，主要优势如下．

(1)对实验环境要求低，在基于耦合腔标准声源对待测阵列进行实测时，实验环境要求低，腔体内的声场特性受环境因素影响小．

(2)避免了由实际小声源的指向性问题和空间尺度引起的测量误差，同时也进一步减少了声源位置的测量误差并提高了测量效率，在实际工程中有广阔的应用前景．

［1］ 贾文强. 基于局部近场声全息的机械噪声源特征提取技术研究[D]. 上海：上海交通大学机械与动力工程学院，2011.

Jia Wenqiang. Fanlt Feature Extraction Technique Based on Patch Near-Field Acoustical Holography[D]. Shanghai：School of Mechanical Engineering，Shanghai Jiao Tong University，2011(in Chinese).

［2］ 梅继丹，石文佩，马 超，等. 近场反卷积聚焦波束形成声图测量[J]. 声学学报，2020，45(1)：15-28.

Mei Jidan，Shi Wenpei，Ma Chao，et al. Near-field focused beamforming acoustic image measurement based on deconvolution[J]. Acta Acustica，2020，45(1)：15-28(in Chinese).

［3］ Brusniak L. DAMAS2 validation for flight test airframe noise measurements[C]//2nd Berlin Beamforming Conference. Berlin，Germany，2008.

［4］ Takaishi T，Inoue T，Lee H-H，et al. Noise reduction design for landing gear toward FQUROH flight demonstration[C]//23rd AIAA/CEAS Aeroacoustics Conference. Denver，USA，2017.

［5］ Yang Y，Liu Y，Li Y，et al. Aerodynamic and aeroacoustic characteristics of a multicopter propeller during forward flight[C]//2018 Joint Propulsion Conference. Cincinnati，USA，2018.

［6］ 唐 俊，汪 照，白宇田. 基于稀疏过零点信息的抗幅值失真时延估计方法[J]. 天津大学学报(自然科学与工程技术版)，2022，55(2)：211-220.

Tang Jun，Wang Zhao，Bai Yutian. Anti-amplitude distortion time delay estimation method based on sparse cross-zero information[J]. Journal of Tianjin University (Science and Technology)，2022，55(2)：211-220(in Chinese).

［7］ Schmidt R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation，1986，34(3)：276-280.

［8］ Zhao S，Saluev T，Jones D L. Underdetermined direction of arrival estimation using acoustic vector sensor[J]. Signal Processing，2014，100：160-168.

［9］ Humphreys J W M，Brooks T F，Hunter J W W，et al. Design and use of microphone directional arrays for aeroacoustic measurements[C]// 36th AIAA Aerospace Sciences Meeting and Exhibit. Reno，USA，1998.

［10］ Chiariotti P，Martarelli M，Castellini P. Acoustic beamforming for noise source localization—Reviews，methodology and applications[J]. Mechanical Systems and Signal Processing，2019，120：422-448.

［11］ Ma W，Liu X. Phased microphone array for sound source localization with deep learning[J]. Aerospace Systems，2019，2(2)：71-81.

［12］ Williams J R. Fast beam-forming algorithm[J]. The Journal of the Acoustical Society of America，1968，44(5)：1454-1455.

［13］ Porteous R，Prime Z，Doolan C J，et al. Three-dimensional beamforming of dipolar aeroacoustic sources [J]. Journal of Sound and Vibration，2015，355：117-134.

［14］ Mukwevho T，Jordaan J，Noel G. Advanced beamforming techniques for acoustic source localization[C]//IEEE Africon Conference. Nairobi，Kenya，2009.

［15］ Cigada A，Ripamonti F，Vanali M. The delay & sum algorithm applied to microphone array measurements：Numerical analysis and experimental validation[J]. Mechanical Systems & Signal Processing，2007，21(6)：2645-2664.

［16］ 褚志刚，杨 洋. 球形传声器阵列三维波束形成性能[J]. 农业工程学报，2012，28(11)：80-85.

Chu Zhigang，Yang Yang. Three-dimensional beamforming performance of spherical microphones array[J]. Transactions of the Chinese Society of Agricultural Engineering，2012，28(11)：80-85(in Chinese).

［17］ 褚志刚，周亚男，王光建，等. 基于声压球谐函数分解的球面波束形成噪声源识别[J]. 农业工程学报，2012，28(增1)：146-151.

Chu Zhigang，Zhou Yanan，Wang Guangjian，et al. Noise source identification by spherical beamforming based on sound pressure spherical harmonics decomposition[J]. Transactions of the Chinese Society of Agricultural Engineering，2012，28(Suppl1)：146-151(in Chinese).

［18］ 褚志刚，杨 洋，蒋忠翰. 波束形成传声器阵列性能研究[J]. 传感技术学报，2011，24(5)：665-670.

Chu Zhigang，Yang Yang，Jiang Zhonghan. Study on the beamforming performance of microphones array[J]. Chinese Journal of Sensors and Actuators，2011，24(5)：665-670(in Chinese).

［19］ Son P L. Irregular microphone array design for broadband beamforming[J]. Signal Processing，2022，193：108431.

［20］ Prasad M G. Aeroacoustic measurements[J]. Applied Mechanics Reviews，2003，56(5)：B66-B67.

［21］ Aldeman M R. A hybrid spiral microphone array design for performance and portability[J]. Applied Acoustics，2020，170：107512.

［22］ 张羽霓，王庆庆，唐 俊，等. 应用于传声器阵列定位校准的空间点声源声场拟合方法[J]. 声学技术，2020，39(4)：445-450.

Zhang Yuni，Wang Qingqing，Tang Jun，et al. Sound field fitting method of spatial point source for microphone array positioning calibration[J]. Technical Acoustics，2020，39(4)：445-450(in Chinese).

［23］ 杜功焕，朱哲民，龚秀芬. 声学基础[M]. 南京：南京大学出版社，2012.

Du Gonghuan，Zhu Zhemin，Gong Xiufen. Fundamentals of Acoustics[M]. Nanjing：Nanjing University Press，2012(in Chinese).

［24］ Ma W，Liu X. Improving the efficiency of DAMAS for sound source localization via wavelet compression computational grid[J]. Journal of Sound and Vibration，2017，395：341-353.

［25］ Ma W，Liu X. DAMAS with compression computational grid for acoustic source mapping[J]. Journal of Sound and Vibration，2017，410：473-484.

［26］ Brooks T F，Humphreys W M. A deconvolution approach for the mapping of acoustic sources(DAMAS) determined from phased microphone arrays[J]. Journal of Sound and Vibration，2006，294(4/5)：856-879.

［27］ Michel U. History of acoustic beamforming[C]//1st Berlin Beamforming Conference. Berlin，Germany，2006.

Performance Evaluation Technology for Microphone Array Based on Spatial Coherent Sound Source Reconstruction

Tang Jun1, 2，Sun Xinmiao1, 2，Li Jiayong1, 2，Yan Lei3

(1. School of Civil Engineering，Tianjin University，Tianjin 300350，China；2. Tianjin Key Laboratory of Port and Ocean Engineering，Tianjin University，Tianjin 300350，China；3. Beijing Aerospace Institute for Meteorology and Measurement Technology，Beijing 100076，China)

The microphone array system based on the beamforming algorithm is widely applied in noise source loca-tion, and its spatial resolution and dynamic range are key performance parameters when it is used to locate multiple sound sources. As a commonly used array performance evaluation method in engineering, the small-scale sound source test method is affected by the size and directivity of the sound source. Therefore, when different sound sources are used to test the same array, the test results usually have large errors, and the test method has high requirements on the environment. On this basis, a spatial sound source reconstruction method based on multi-channel standard coupled cavity sound source is proposed in this paper, which can reconstruct a spatial point sound source of any position, fre-quency and intensity. This point sound source is output by the standard coupled cavity to the microphone sensor of the corresponding coordinates, and the reconstruction of two coherent point sound sources can replace the actual spatial small-scale sound source to measure and analyze the performance parameters of the microphone array. A 30-channel spiral microphone array commonly used in engineering was selected for conducting numerical simulations, a standard coupled cavity experiment and a contrast experiment with an actual small-scale sound source. In the 2—4 kHz fre-quency band, the test results of multi-channel coupled cavity standard coherent sound sources on the array were highly consistent with the numerical simulation results, indicating the effectiveness of the proposed method. The results of contrast experiment with the actual small-scale sound source show that the reconstruction method of coupled cavity standard sound source was less affected by the test environment. When this method was used to analyze the perform-ance of microphone array, the measurement error was small and the accuracy was high.

microphone array；sound source reconstruction；spatial resolution；dynamic range；beamforming

10.11784/tdxbz202210004

O422.2

A

0493-2137(2023)08-0860-10

2022-10-06；

2023-02-21.

唐 俊（1979—  ），男，博士，副研究员.Email：m_bigm@tju.edu.cn

唐 俊，tangjun@tju.edu.cn.

国家重点研发计划资助项目(2020YFA0405700).

the National Key Research and Development Program of China(No. 2020YFA0405700).

(责任编辑：武立有)