基于双层模型预测控制的微电网经济调度
2023-06-20舒晓欣林其友王庆华
舒晓欣,林其友,张 健,田 佳,王庆华,周 丹
(1.国网芜湖供电公司,安徽 芜湖 241000;2.国网淮北供电公司,安徽 淮北 235000;3.国网安徽省电力有限公司,安徽 合肥 230001;4.浙江工业大学 信息工程学院,浙江 杭州 310023)
近年来,由于化石燃料价格的不断上涨以及偏远地区用电量的不断增长,可持续能源系统的需求也日益增加,利用含分布式电源的微电网供应系统解决方案可以有效降低系统的运行费用[1],分布式能源发电受到了越来越多的关注。自治能源供应系统的应用包括紧急备用系统、偏远地区电信塔站、军事应用和海岛供电等。目前,国内外学者针对提高微电网运行经济效益方面的研究主要采用确定性优化和随机优化两类方法。确定性优化通过采用蒙特卡洛法和场景法[2]将微电网经济调度问题转化为多代理协同问题或非线性规划问题进行求解。支娜等[3]引入代理商来对微电网元件进行建模,并通过各个代理商之间的竞价实现微电网的最优调度。也有研究利用启发式搜索方法,来实现模型的求解,如混合量子遗传算法[4]、多周期引力搜索[5]和粒子群优化算法[6]。高佳等[7]引入分段非线性惯性系数改进粒子群算法从而更为快速有效地求得多元互补微电网运行优化结果。而随机优化则采用概率学方法构建随机规划模型来获取具有一定鲁棒性的可行解。刘一欣等[8]采用鲁棒优化来处理微电网运行中的不确定性,但由于考虑了最恶劣场景下的可行性使得所得结果偏于保守。而模型预测控制(Model predicted control,MPC)由于其适应性和对不确定性问题的鲁棒性而引起关注。Parisio等[9]利用模型预测算法对包括电池组和柴油发电机系统最优运行的线性混合整数优化问题进行了求解。Palma等[10]采用基于神经网络预测算法的MPC对孤岛微电网经济运行进行求解。然而上述研究并未考虑实际中存在的众多干扰因素,且由于描述模型方程的过度简化而导致功率调度存在误差问题,如电池组模型常不能提供或吸收所需的所有功率并以低效的方式运行,非线性组件模型的线性近似导致高功率损耗和次优控制[11]。
基于上述分析,为了提高微电网对于预测误差及系统不确定性的鲁棒性,在同时考虑长期和短期两阶段递归优化的前提下,提出基于双层MPC的微电网经济调度方法。建立电池组充放电控制策略的微电网调度优化模型,并将MPC控制引入到在实时负荷和光伏功率预测的权重因子更新过程中,从而改善了模型的自适应性和准确性。
1 微电网模型
系统包括光伏、电池组和柴油发电机,为了实现离网能源系统可靠的在线控制,需要对所有组件搭建合适的数学模型,以确保将由建模误差引起的不确定性保持在最低限度。
1.1 光伏模型
光伏发电机基于太阳辐射产生输出电流,需要考虑模块中的温度变化。基于能量平衡方程,模块温度Tmod的动态方程为
(1)
式中:Cmod>0为热容量;G为吸收的辐射;Qrad为辐射传热;Qconv为对流传热;Pel为产生的电功率。对于其中的二极管模型,光伏模块的电压VPV的推导计算式为
Vdiode(t)=VOCmod(t)(1+αVOC(Tmod(t)-TSTC))
(2)
VPV(t)=Vdiode(t)-IPV(t)Rseries
(3)
式中:Vdiode为二极管电压;VOCmod为模型开路电压;IPV为温度校正系数;IPV为标准测试条件(STC)下的温度;IPV为电流;Rseries为串联电阻。电流计算式为
IPV(t)=
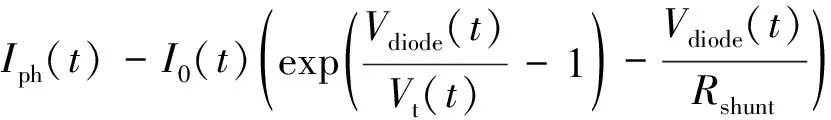
(4)
式中:Iph为太阳照射下的电流;I0为二极管反向饱和电流;Vt为端电压;Rshunt为分流电阻。电压计算时选择VOCmod∈{0,VOCSTC}确定最大功率点,最大功率跟踪点(Maximum power point tracking,MPPT)处的光伏功率为PPV=IPV(t)VPV(t)nmnst,包括部件数nst和每个部件中的模块数nm。
1.2 电池组模型
电池组的关键物理特性是其标称电压和荷电状态(State of charge,SOC),在不同参数设置情况下,带有附加归一化容量系数的基本Shepherd方程式为
Vb(t)=E0,c-gc(1-xSOC(t))+
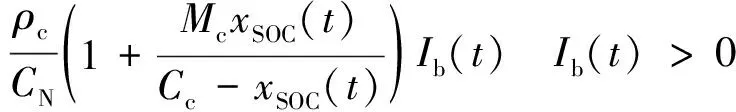
(5)
Vb(t)=E0,d-gc(1-xSOC(t))+
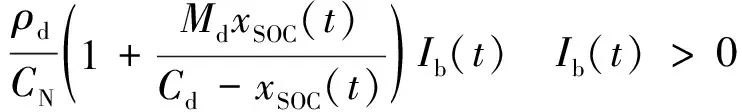
(6)
式中:CN为标称电池组容量;E0,c/d为充放电时电池的开路电压电平;gc/d和Mc/d为充放电时电池的电解液上的比例常数;ρc/d为充放电时电池的容量电阻值;Cc/d为充放电时电池的归一化容量系数;xSOC为充电状态。
电流Ib计算式为
(7)
(8)
Icell=
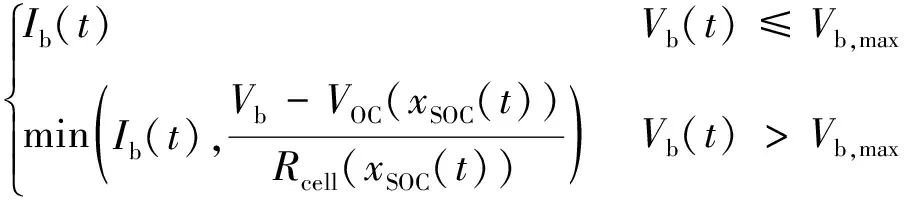
(9)
式中:Pb为从电池组施加或吸收的功率;Icell为电池组的电流;Vb,max为截止电压。
1.3 分布式柴油发电机模型
柴油发电机模型有连续和离散两种状态,其特征与对应的关闭时间δtoff,i∈{0,1,…,δtoff,max}对应,发电机运行状态(开/关)δstate,i∈{0,1}且输出功率为Pdg,i,其中i∈{0,1,…,Ndg}(Ndg为发电机数量)。关闭时间定义为
(10)
只要δtoff,i的值小于最小关闭时间,发电机输出功率就等于零。为了确定柴油发电机的运行成本,引入发电机的启动/关停状态辅助变量δu/d,i,计算式为
δu,i(tk)=δstate,i(tk)(1-δstate,i(tk-1))
(11)
δd,i(tk)=δstate,i(tk-1)(1-δstate,i(tk))
(12)
2 双层模型预测控制模型
提出的双层MPC方法,包括离散动态规划(Discrete dynamic programming,DDP),以在可接受的时间范围内寻求最优解。在第二层控制中通过调整柴油发电机的运行提高控制对预测误差的鲁棒性。为了展开所提的两层模型预测控制方法,提出一种用于负荷和光伏发电预测的自适应预测算法。
2.1 光伏发电和负荷预测
MPC方法可以确定24 h内能源系统的最优运行状态,在计算过程中,需要预测第二天的光伏功率和负荷需求,并在每次迭代时更新。在没有与电网连接,没有网络或天气预报接入的偏远地区能源系统中,光伏发电和负荷需求的预测一般基于前几天的数据。因此,使用的预测算法提出了一种在偏远地区的微电网系统能够实施的有效方法。该方法由季节性自回归综合移动平均模型(Seasonal auto regression integrated moving average model,SARIMA)和指数平滑方法组成。SARIMA模型是自回归移动平均(Auto regression moving average,ARMA)模型的扩展,用于描述具有非平稳均值和季节性行为的时间序列,选择SARIMA模型的原因在于其对不同负荷断面的适应性,适用于预测天数多且参数少的情况。SARIMA模型可表示为
φP(L)Φ(Ls)(1-L)(1-Ls)yk=θqΘQ(Ls)ak
(13)
式中:Lyk=yk-1为滞后算子;ak为随机冲击系数;φP(L),θq(L),Φ(Ls),ΘQ(Ls)定义为符合顺序的滞后算子的多项式,其中s为季节性程度。
多项式中的所有参数采用负荷/光伏数据训练集确定,选择包括功率曲线变化的随后30天进行参数确定。趋势程度(1-L)、季节性分量(1-LS)以及滞后项的阶数由系统情况和部分自相关函数确定。
2.2 双层模型预测控制
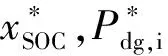
2.2.1 模型预测控制
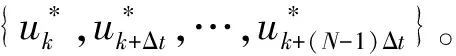
2.2.2 离散动态规划
用于解决优化问题的DDP基于Bellmans最优性原理[12],该最优性原则指出,在最优决策序列问题中,每个子序列也必须是最优的,将优化问题分解为多个子问题,这些子问题单独求解,可得到整个优化问题的全局最优解。所有状态和输入变量以及优化范围都是离散化的,其计算时间仅随着范围大小线性增加,因此可使用短的采样时间和长的仿真范围。
为了保证多个柴油发电机有足够的计算时间,通过引入柴油发电机可能输出功率的误差区间实现对搜索空间的限制,一台发电机的搜索空间如图1所示。通过对一台或多台发电机进行优化分析得到平均负荷需求功率和柴油发电机平均输出功率,分析结果表明发电机通常在负荷需求附近的某个间隔内运行。新的搜索空间包括误差区间以及附加的发电机无功率输出即处于关闭状态。虽然无法保证最优解位于此间隔区间内,但仿真结果表明,对于额定功率的±20%间隔,最优解仍然处于可能的组合内。参考状态每10 min更新一次,要是没有这种限制,只有一个发电机的系统能够满足9 s的计算时间要求,其中具有两个发电机的系统则需要200 s计算时间。DDP能够保证找到离散化优化问题的全局最优,因此适用于所提的包含中等数量源的非线性混合整数优化问题。
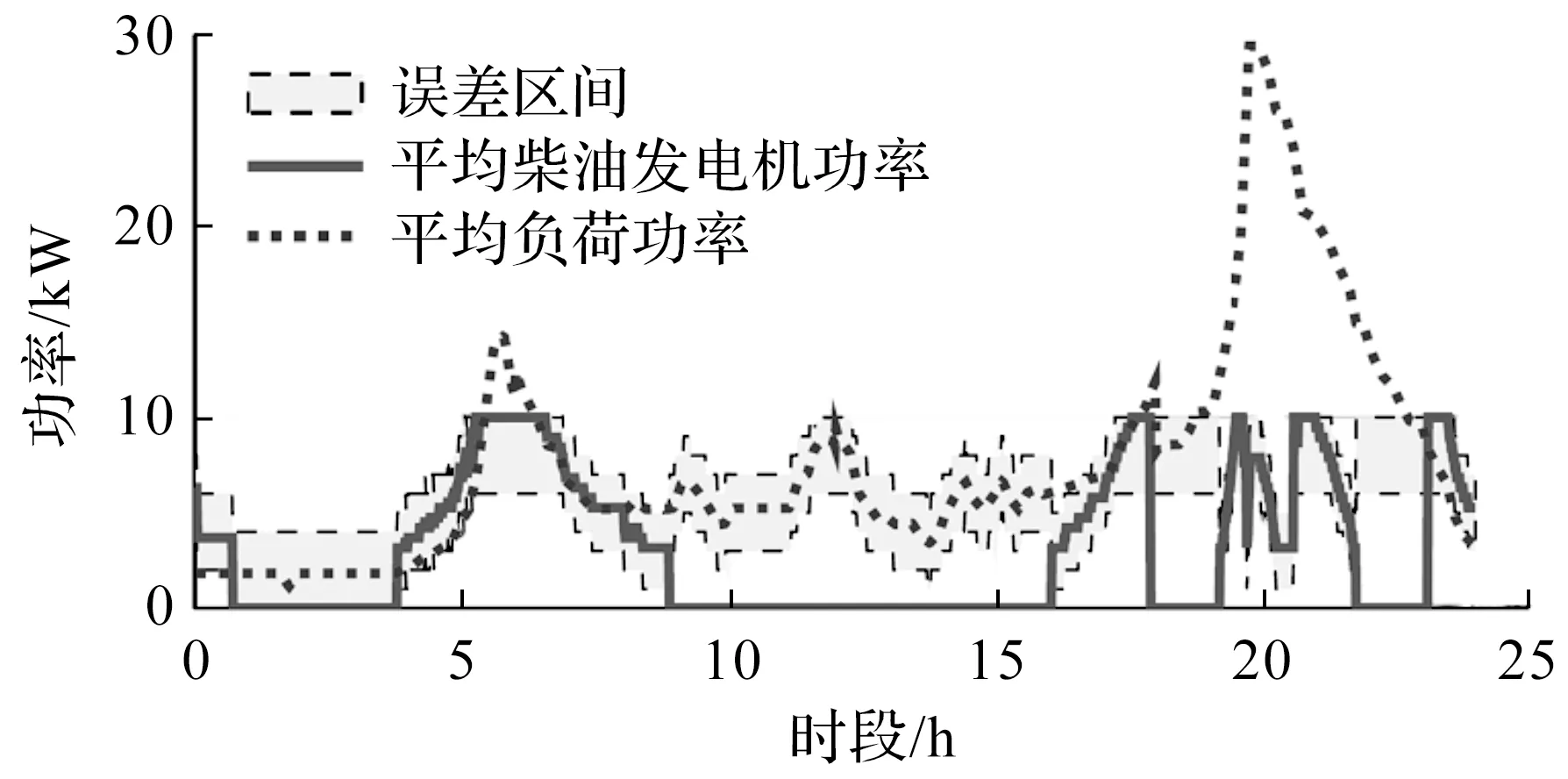
图1 10 kW柴油发电机的搜索空间范围
2.2.3 边界值问题
第二层优化用于处理预测误差或者光伏功率的波动问题。与第一层优化不同,第二层采用连续而非离散的状态变量来计算开/关时间,该层包括柴油发电机开/关时间切换的BVP优化问题,使用实际系统状态以及负荷需求和光伏功率的预测来计算开/关时间的切换。与之前的MPC方法相比,这里每2 min进行一次递归计算,通过最小化状态终点之间的误差使得参考SOC状态和实际状态相匹配。只要一个10 min时间间隔,包括发电机的启动/停止时间、发电机最长关闭时间或正在运行,就会激活第二层优化。这进一步使发电机能够启动或关闭,即使在第一层没有计算启动/停止时间。因为第一层中已知最佳控制轨迹的形状以及柴油发电机功率,所以可将计算柴油发电机开/关时间的优化问题表示为BVP形式,开/关时间是优化的唯一变量。令开启时间为tONi,柴油发电机功率切换方式可定义为
(14)
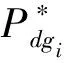
电池组动力学的BVP动态方程为
(15)
(16)
(17)

BVP边界条件为
(18)
(19)
柴油发电机的开/关时间的切换可以在数值上计算得到对应的切换功率并应用于系统,该计算每2 min递归执行一次,其中开/关时间每10 min计算一次,每次迭代时更新负荷和光伏功率的预测值。采用打靶法求解BVP时,将原始的BVP问题转换为了初始值问题(Initial value problem,IVP)。最小化MPC中确定的SOC参考轨迹的端点与预测的SOC轨迹之间误差时可能会出现一些问题,因为不一定达到参考的SOC值,而IVP公式则可以克服该问题。
3 算例仿真
验证分析所提的实时控制方法对不同环境条件、光伏功率和负荷需求的适应性。光伏功率曲线以及负荷曲线不仅包括两天内功率输出的变化,还包括了一天内太阳能数据的变化。结合天气情况得到的负荷曲线如图2所示。光伏、电池组和柴油发电机的参数如表1所示。
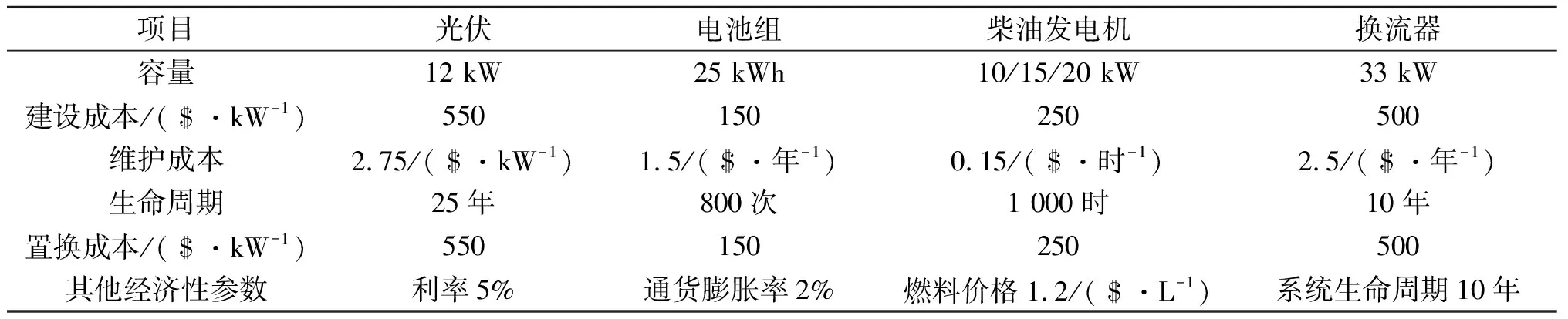
表1 各元件基本成本参数
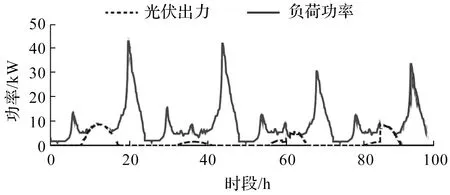
图2 3天内的负荷和光伏功率曲线
考虑5 d内的最优功率分配问题。预测误差选取为24 h内预测值与实际值之间误差之和,该计算在第一层优化中实现,结果如表2所示。由表2可知使用自适应预测模型可以降低预测误差的平均值和最大值。

表2 有无自适应权重预测算法对比
假设已知光伏功率和负荷需求,由DDP确定的最优柴油发电机和电池组的状态与使用双层MPC方法确定的柴油发电机输出功率的比较的曲线如图3,4所示,该方法将最优调度问题与柴油发电机的开/关时间切换问题相结合。由图3,4可以看出:比较柴油发电机的最优运行状态与MPC方法确定的状态,两种情况下发电机之间的功率调度平均仅相差0.54~1.09 kW。笔者所提的两层在线控制得到的柴油发电机输出功率和离线计算的最优控制的功率轨迹在大多数时间保持一致。由于负荷需求的大幅变化和光伏功率预测误差导致柴油发电机的附加启动,会降低控制对预测误差的灵敏度,因此在所提方法中引入第二层优化。此外,对能源系统进行适当的数学描述,包括所有部件的相关特性和运行约束,从而限制了建模误差,使得能够进行合适的实时控制,并应用于实际系统。图4中,电池组功率最优结果与MPC解决方案之间存在略微的偏差,这是由柴油发电机的不同操作引起的。然而,电池组总是能够提供多余的能量以保证不间断的电力供应,所提方法可以在线实施,在高水平上计算所有组件的最优功率调度和功率设置,其中较低级别的附加控制器用于控制瞬时动态。
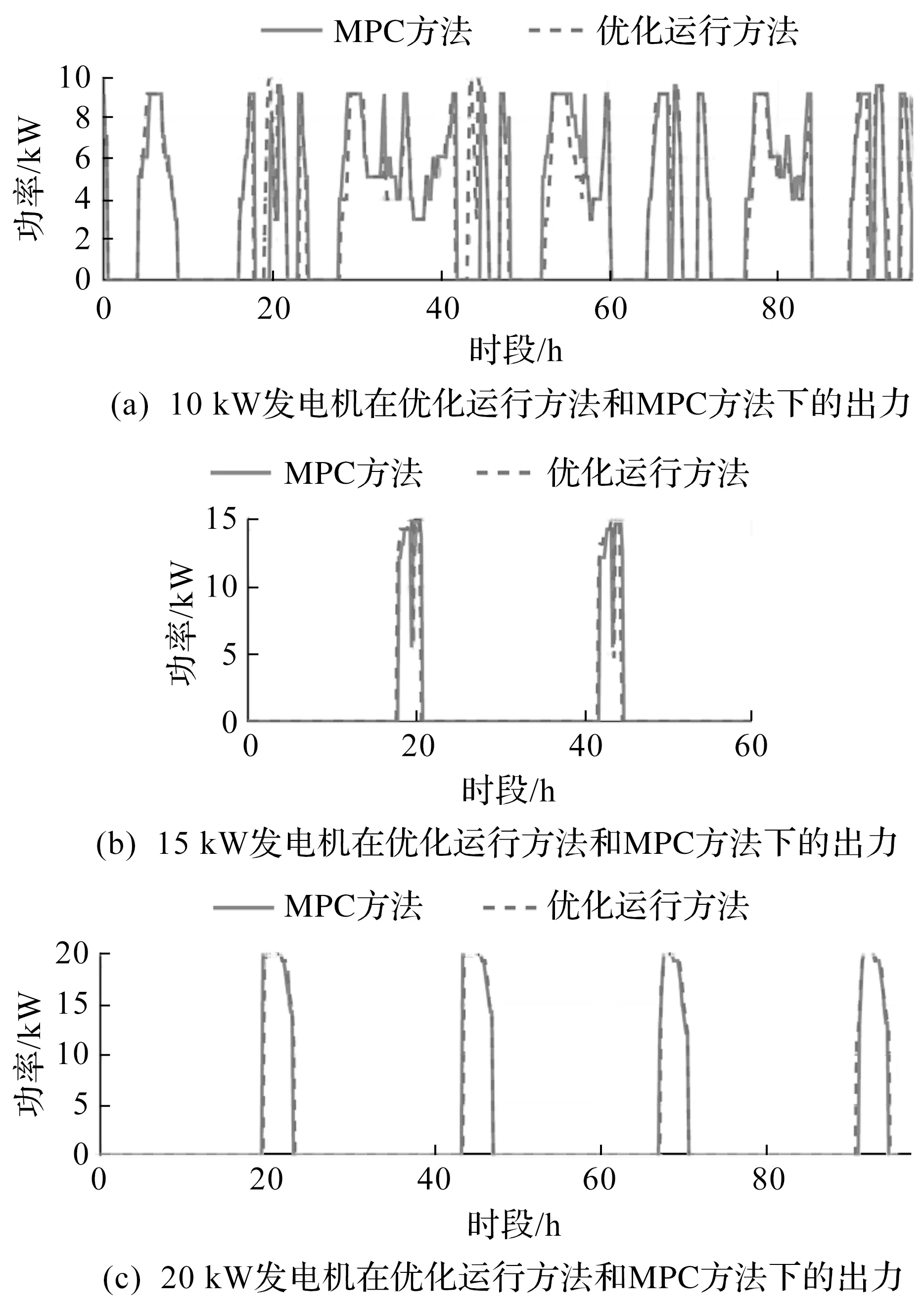
图3 优化运行方法和MPC方法下的发电机最优输出功率
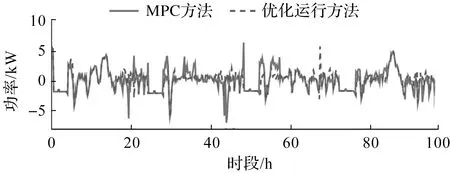
图4 电池组在优化运行方法和MPC方法下的出力对比
4 结 论
提出了一种有效的两层模型预测控制方法,用于呈现混合孤岛能源系统特征的微电网的在线控制,通过算例分析得出模型预测控制的经济调度方法能够最小化运行成本并提高对负荷需求和光伏功率引起的不确定性问题的鲁棒性,包含所有重要系统特性有助于进行适当的在线控制;提出的控制策略增加了微电网对不确定性的鲁棒性,满足所有复杂的运行约束并且计算成本低廉,因此适合于微电网的实时控制。
