含未知控制方向的多智能体系统输出同步控制

陈宇翔,彭钧敏

(1.义乌工商职业技术学院 建筑工程学院,浙江 义乌 322000;2.湖南工业大学 电气与信息工程学院,湖南 株洲 412007)

由于多智能体的广阔应用背景,自21世纪以来,多智能体的协同控制引起了控制界的广泛关注。早期的相关工作聚焦于具有线性模型的个体,或一阶非线性个体。目前,多智能体系统中个体模型是非线性系统的情形正在为研究者所关注,如分数阶系统、链式系统、随机系统、下三角系统、非标准三角系统、欧拉—拉格朗日系统和具有准单侧李普希茨非线性动力学的系统等。此外,不确定性和扰动可以更准确地反映系统实际情况,包括不可测的速度信号、输入约束、未建模的动态以及随机扰动等情形也被同时考虑在内。当多智能体系统中个体为高阶系统且含有不确定性时,目标将从状态一致变更为输出同步。高频控制增益的符号,即控制方向,直接决定了控制是正反馈还是负反馈,对于系统的性能十分重要,已有的研究通常假设其符号为正,而在某些实际系统,如舰船姿态控制、硬盘伺服系统中,其符号是未知的,因此,在控制方向未知条件下如何对系统进行控制就成为了一个难题。Nussbaum[1]提出用Nussbaum函数处理未知控制方向的基础上,Jiang等[2-7]的研究逐步将这一方法推广应用至高阶非线性系统,且考虑未知参数等情形。随着多智能体系统研究的深入,Peng等[8-12]逐步将此类未知控制方向的系统模型引入到多智能体系统中,以考虑其协调控制问题。

相较于现有研究成果[9-12],笔者研究取消了对未知控制方向的诸多假设和限制,即智能体可以有不同且相异的控制方向,而控制器的设计并不需要提前知道控制方向的相关先验信息。在传统李雅普洛夫函数构造中,Nussbaum函数会在求导之后出现[3-5],笔者构造了一种新型的分析函数,即Nussbaum函数直接出现在分析函数中,而非其导数,不仅可以简化证明过程,而且可以扩大此方法的适用范围。

1 预备知识与问题描述

1.1 预备知识

1.1.1 符号定义

在笔者研究中,Rm×n表征i实矩阵。M≥(≤)0表示M是正(负)半定矩阵,M>(<0)表示M是正(负)定矩阵。Null(M)表示矩阵M的零空间,sup(·),inf(·)分别表示最小上界和最大下界,符号sing(·)是经典的符号函数。对于连续可微函数f:Rn→R,行向量∂f/∂x为[∂f/∂x1,∂f/∂x2,…,∂f/∂xn]。

1.1.2 图论相关知识

加权图用G=(V,E)表示,其中V={1,2,…,N}是一个由n个节点组成的非空有限集合,边集E⊆V×V被用来描述智能体之间的通信。其中节点i的邻居集用Ni={j|j∈V,(i,j)∈E}表示。j∉Ni意味着不存在节点j到节点i的路径。一系列边{(i,k),(k,l),…,(m,j)}代表存在一个节点i到节点j的路径,对于无向图来说,如果对于任意节点i,j∈V,存在由节点i到节点j的路径,则称该图是联通的。

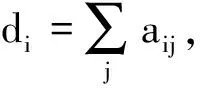
1.1.3Nussbaum函数

Nussbaum函数是具有下列性质的函数,表达式为

(1)

常用的Nussbaum函数包括ek2cos(k),k2sin(k)和k2cos(k)等。

1.2 问题描述

1.2.1 已知条件

考虑一个由n个个体组成的多智能体系统,个体i的模型表达式为

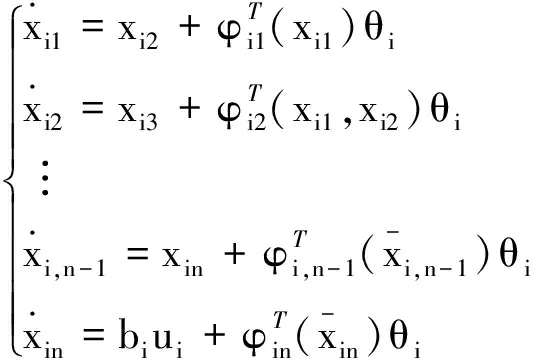
yi=xi1i=1,2…n

(2)

1.2.2 控制目标

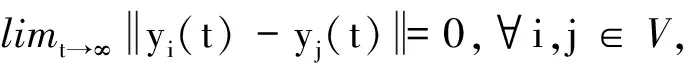
2 控制器设计

对于模型如式(2)的个体i,设计分散控制器,其表达式为

(3)

(4)

其中

(5)

其中a2,a3,…,an>0;函数φim,wim,ψjm表达式分别为

(6)

参数估计器更新率计算式为

(7)

(8)

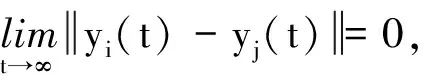
3 理论证明

第一步:定义

(9)

可得Vi1沿式(2)的导数为

(10)

进一步,将式(10)改写为

(11)

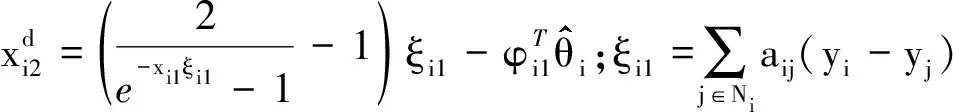
(12)

(13)

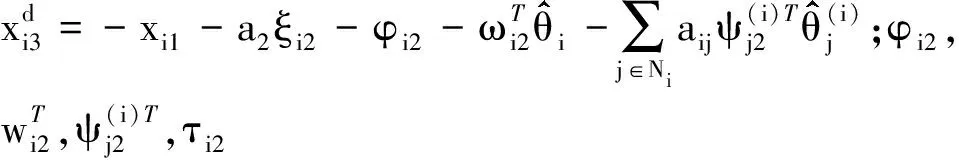
(14)

(15)

通过式(12,14),有

(16)

式中γ1,γ2>0为控制增益。

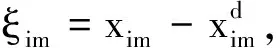
(17)

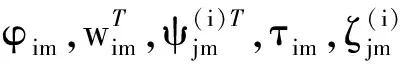
(18)

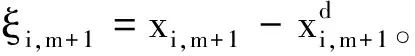
(19)

可得

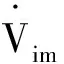
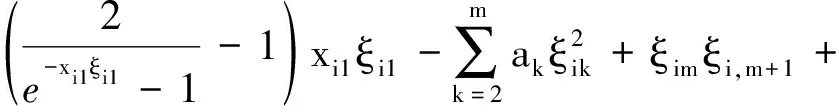
(20)

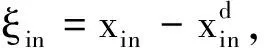
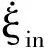
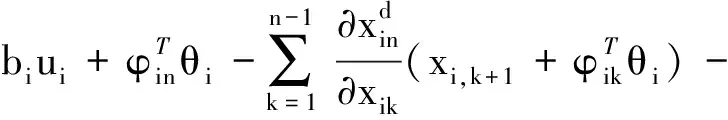
(21)

定义

(22)

注意到

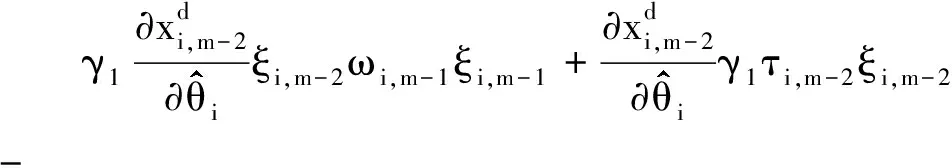
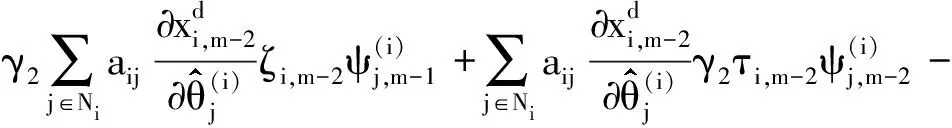
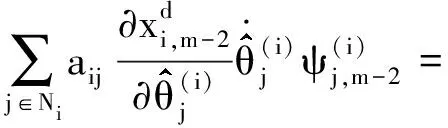
(23)

Vin的导数为

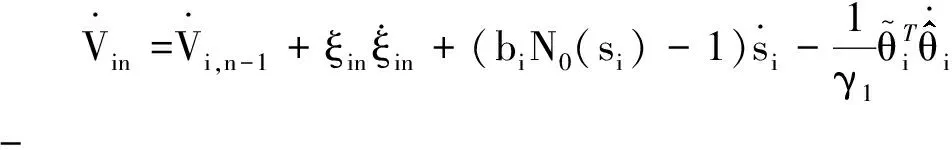
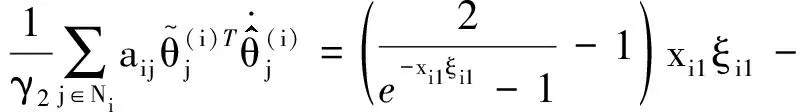
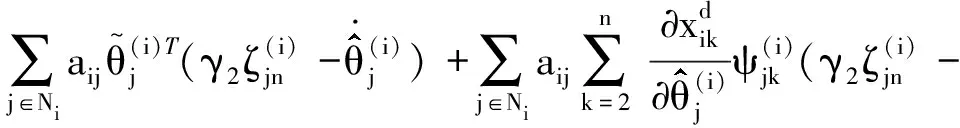
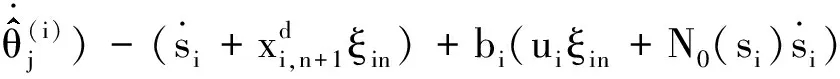
(24)

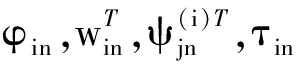
(25)

接下来,将采用反证法证明时间区间[0,+∞)上闭环系统解的存在性。

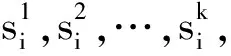
(26)

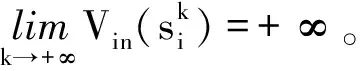
(27)

此外

(28)

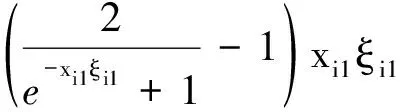
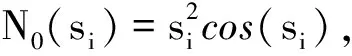
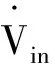
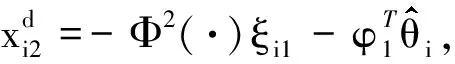
4 仿真结果

通过一个仿真案例来验证笔者提出的控制器的有效性。考虑一组3个个体的输出同步问题,个体在图1中用‘1～3’表示。为了简单起见,当aij>0时,将aij设置为1。个体i的动态模型为

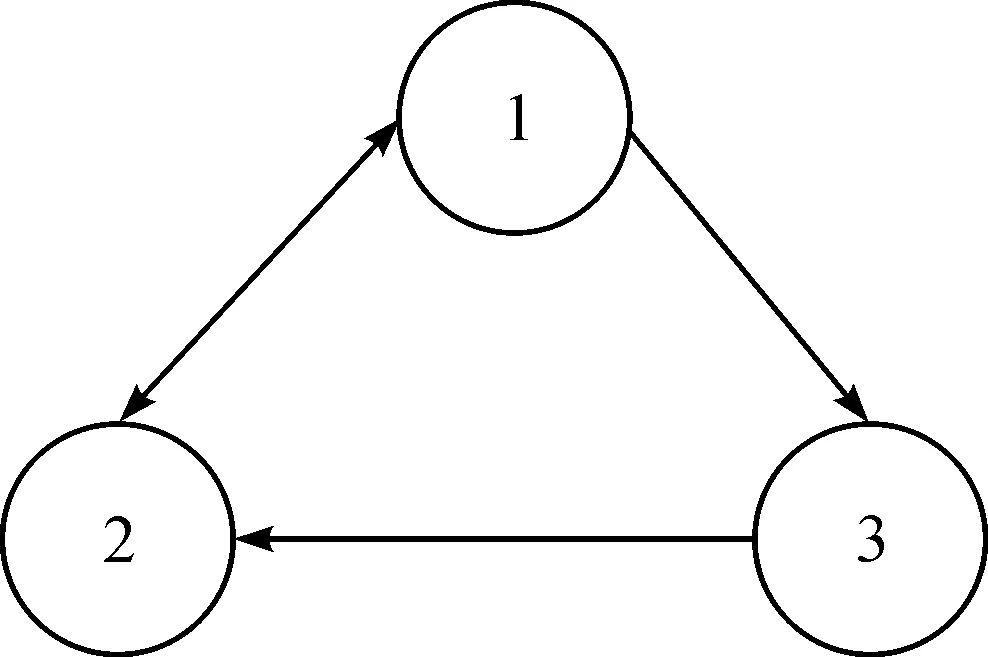
图1 多智能体系统通信拓扑图

(29)

对于xi=[xi1,xi2]T,yi和ui分别为个体i的状态、输出和输入;不确定参数bi的符号代表控制方向,同样未知;θi为未知参数。

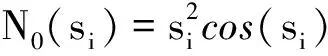
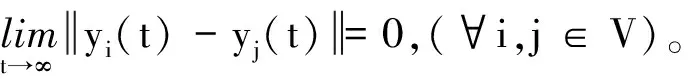
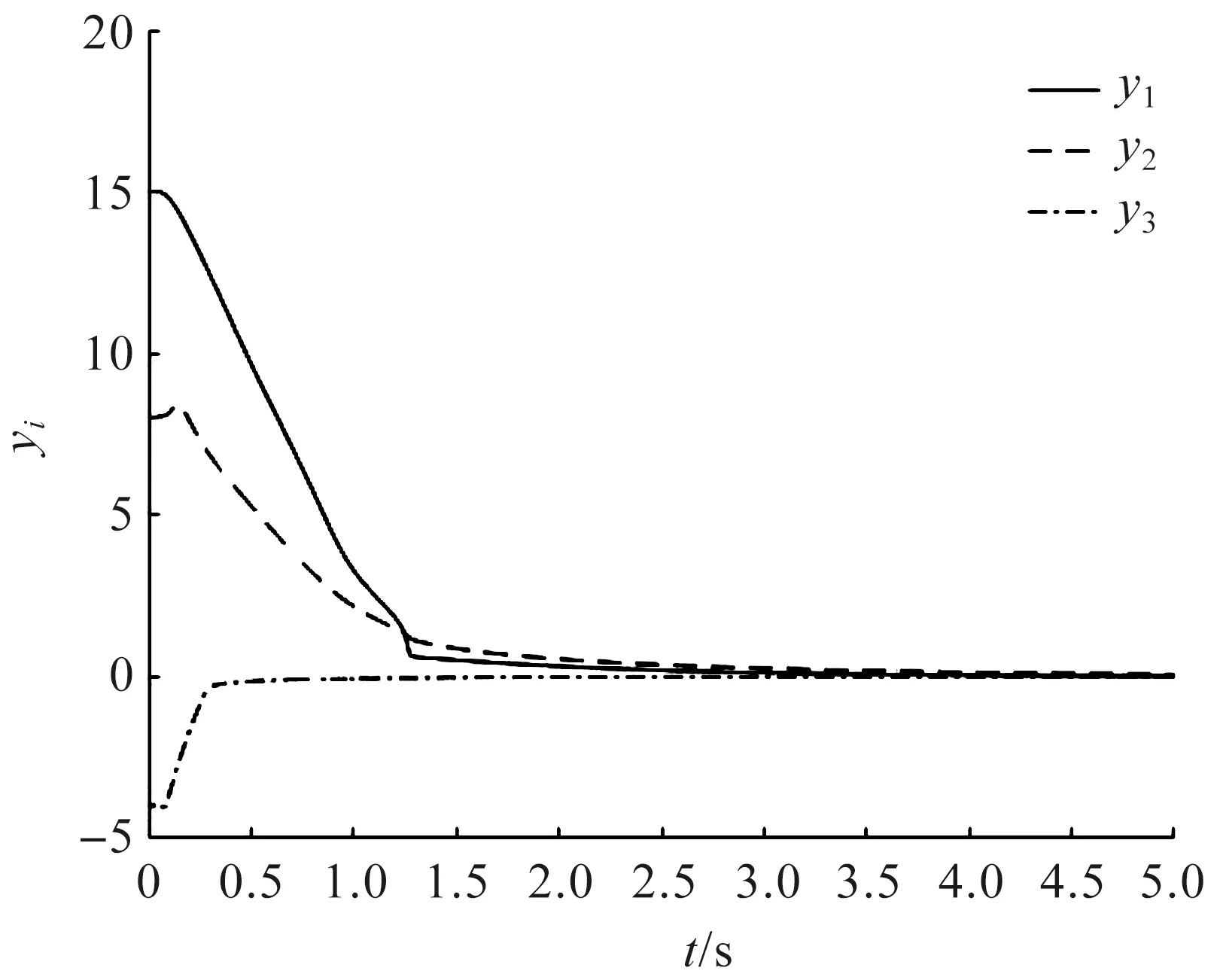
图2 个体输出轨迹yi(t)(i=1,2,3)

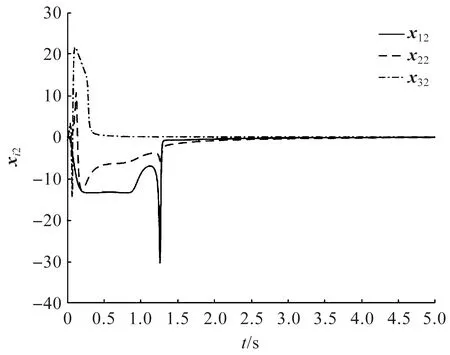
图3 个体状态xi2(t)(i=1,2,3)

图4 状态量si(t)(i=1,2,3)

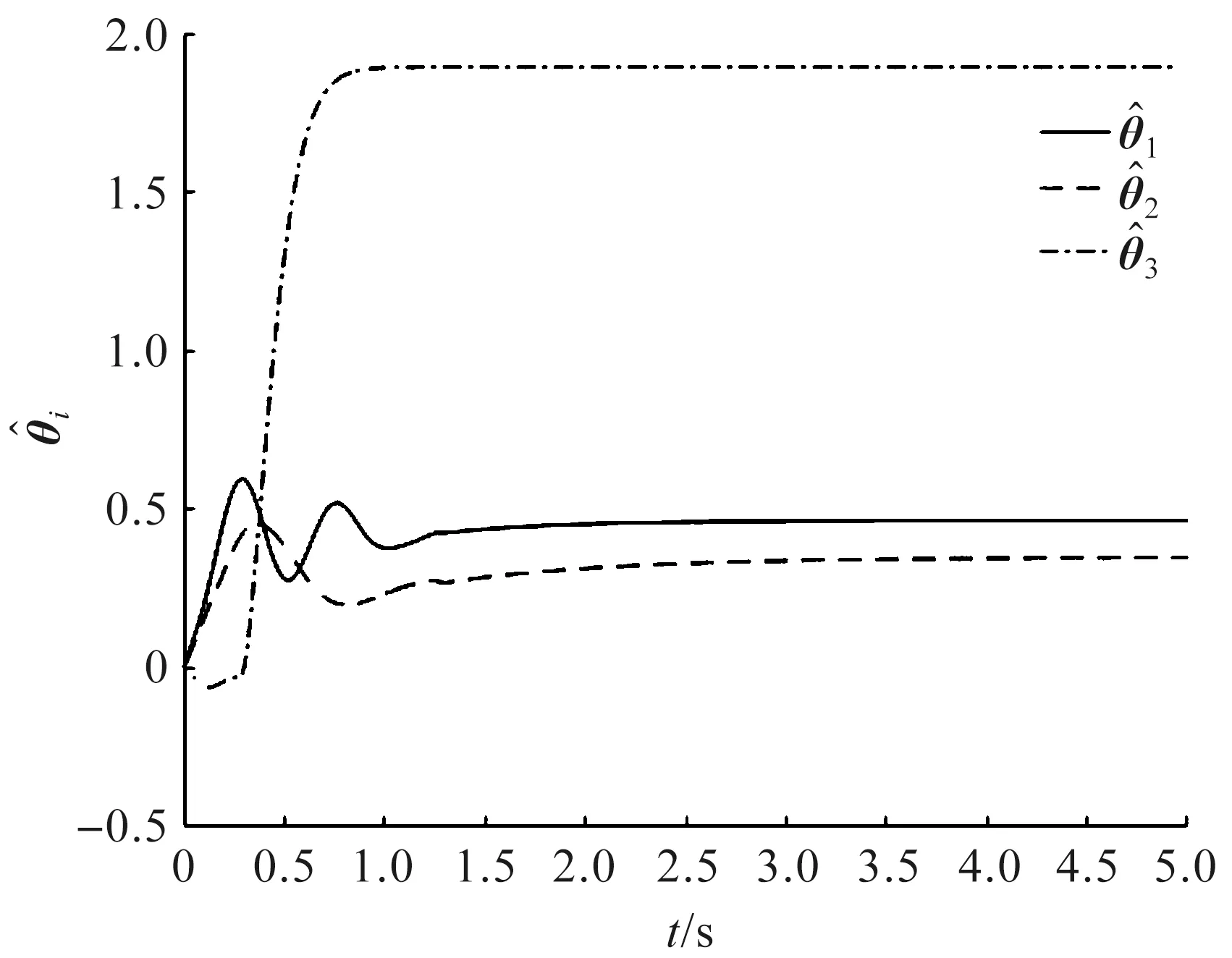
图5 参数估计器

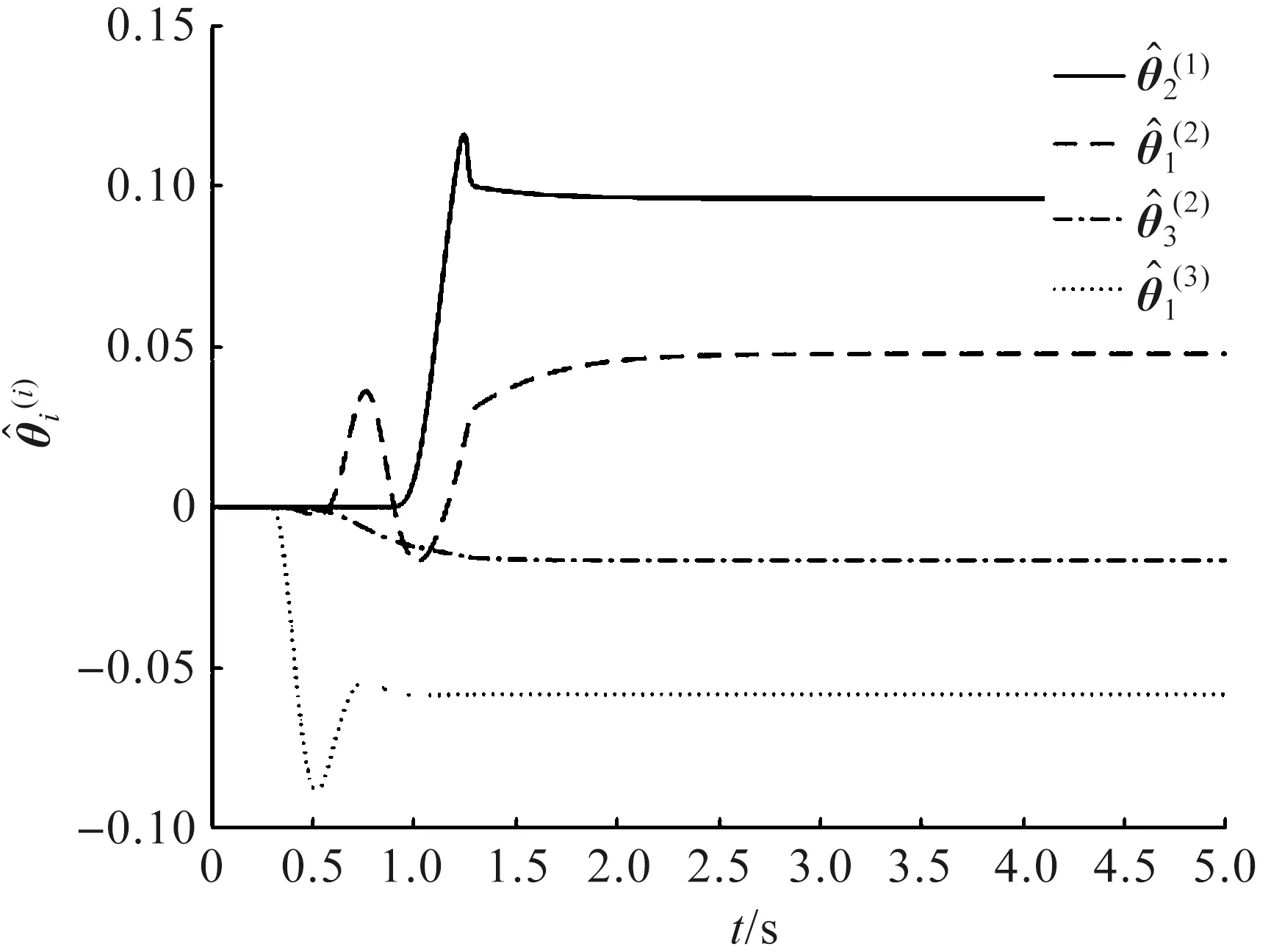
图6 参数估计器

笔者未来的研究方向将聚焦于这种具有时变延迟的多智能体系统的收敛速度[18]和非严格反馈形式的个体模型[19]。

5 结 论

笔者研究了具有参数不确定性和未知控制方向的多个严格反馈系统构成的多智能体网络系统的输出同步问题,其中通信拓扑为有向图结构。首先,为每个个体用反推方式设计了一个分散控制器,在实现输出同步的同时保证整个系统有界;其次,提出了一种新的分析函数构造方法,即Nussbaum函数项直接出现在分析函数本身,而不是其导数中,从而可以简化证明过程。仿真案例表明了笔者方法的有效性,后期将应用至超级电容储能系统,以实现故障模式(即发生某些超级电容单体极性反转)下的电压均衡控制。