从“数学本质”视角看“三角形中位线”

广州市花都区教育发展研究院(510800) 王进

新课标(2022 版)强调以学生发展为本,以核心素养为导向,要求整体把握教学内容,强化数学本质的理解.本次课标修订中的课程内容架构,呈现实施以“大概念”、“大单元”理念为主要理论支撑的课堂教学设计.“核心素养”、“核心知识”、“大单元设计”等一系列在课标中高频出现的词汇,其共同指向的就是要抓住学科的本质,数学课堂教学需要从零散概念中,理清数学知识的内在逻辑,提炼出数学的本质问题,这样才能将能设计出符合学生深度学习需求的数学课堂[1].笔者在执教“三角形的中位线”一课时,基于数学知识内在逻辑,基于深度学习需要,基于数学知识本质,从“数学本质”分析为切入点,理清“三角形的中位线”知识的内在逻辑,设计数学味浓、逻辑性强、注重素养的深度学习课堂.

1 数学本质一: 三角形中位线是“三角形”和“平行四边形”的“桥梁”

我们认识特殊图形的逻辑往往是: 由整体到局部、化未知为已知,在平行四边形的学习中我们是由定义推导出平行四边形的性质和常用判定.在研究过程中,我们往往做辅助线的方法将平行四边形转化为三角形.反之三角形我们可以通过“中位线”的分割,找到三个平行四边形.所以其数学本质为: 平行四边形转化为三角形易研究;三角形用中位线分割可转化为平行四边形(而且也分割成四个全等三角形)[2].

1.1 基于数学本质的探究活动一: 引入三角形中位线的定义

1.1.1 联系实际与旧知: 回顾平行四边形的研究思路

师问: 前几节课我们研究哪些知识?

答: 研究了平行四边形的定义、性质、判定

师问: 在由平行四边形推导其性质和常用判定时,我们往会作怎样的辅助线? (可提示: 如何由“两边平行”推导到“两边相等”的)

答: 作对角线来构建全等三角形

师总结: 在研究平行四边形时往往转化为三角形来研究

1.1.2 画图感受,发现问题

(1)画一画: 按要求画图.①把平行四边形面积两等份;②把平行四边形面积四等份;

学生常用等分方法一:

学生常用等分方法二:

【对比以上方法】

让学生分析利弊: 大部分学生都会选择连对角线,这样是利用平行四边形图形特点,较容易操作,而分割成平行四边形需要取中点、平移线段,相对麻烦.

以上研究结论: 平行四边形转化为三角形是常用、可行、易操作的研究问题方式.

1.1.3 引导学生逆向思考

(1)今天我们来逆向思考,你能否将三角形分割成面积两等份和四等份?

(2)画一画: 按要求在以下画图区画出图形

【学生常有的分割方式】

面积两等分

面积四等分

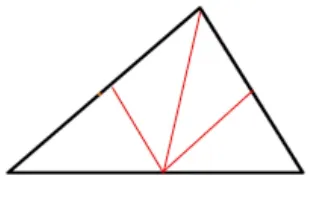
面积四等分

教师引导: 能否分成四个形状和面积都一样的图形? (如上图)

总结在研究平行四边形时往往会转化成三角形,因为转化为三角形后易研究,而三角形中位线的可将其分成四个全等的三角形,这里可以找到三个平行四边形,这种分割是对三角形的一种完美的分割.

1.1.4 给出三角形中位线定义

如上右图,ΔABC中,D,E分别是边AB,AC的中点,连接DE.像DE这样,连接三角形两边中点的线段叫做三角形的中位线.

2 数学本质二: 三角形中位线的研究是从局部(三角形)回归到整体(平行四边形),呈现了数学问题的对立和统一

三角形中位线既是对三角形的特殊线段的研究,也是将三角形的问题回归到平行四边形问题的一种路径.如下图方式一: 三角形的三条中位线完美的分割成四个全等的三角形,同时也得到三个平行四边形,方式二: 一条中位线分割成一个三角形和一个梯形,可拼成一个平行四边形.之前是“整体”到“局部”,现在是“局部”到“整体”,这也体现了数学问题的对立与统一.

方式一:

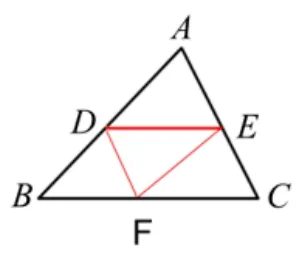
可得.ADFE、.BFED、.DFCE.

方式二:

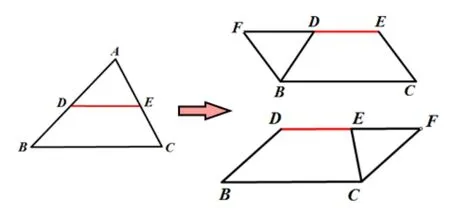
可得.ADFE,.DFC B.

2.1 基于数学本质的探究活动二: 探索三角形中位线定理

教师提问: 观察DE为ΔABC的中位线,DE与哪条线段存在特殊关系?

教师引导学生: 两条线段的关系往往可以从“位置”与“数量”思考.

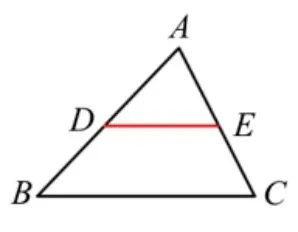
2.1.1 提出数学问题

如图: 在ΔABC中,D,E分别是边AB,AC的中点,

求证:DE//BC,DE=

2.1.2 思路自然生成

思路一: 从平行入手

经验告诉我们“判别平行”往往从“角相等”(同位角、内错角、同旁内角)来入手,而证明角相等可通过证全等,但此时的同位角(如: ∠ADE与∠B)所在的ΔADE与ΔABC并不全等,需其他思路.

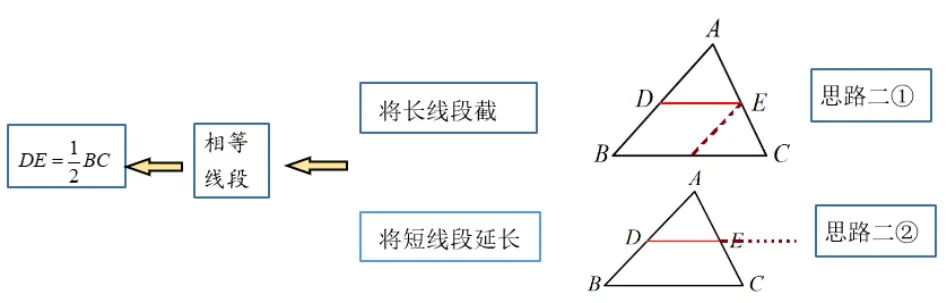
思路二: 从线段长短入手

长线段与短线段的倍数关系,可将长线段截短或将短线段延长,构建全等三角形,证明线段相等.

①将长线段截短(如图思路二①)此时又多了一条中位线,证全等的难度增加.

②将短线段延长(如图思路二②),可构建易证的全等三角形,可理解为将ΔADE旋转至梯形DBCE右侧,构建出平行四边形,是可行的方法.

2.1.3 严格规范论证

证明如图,延长DE到F,使DE=EF,连接CF.

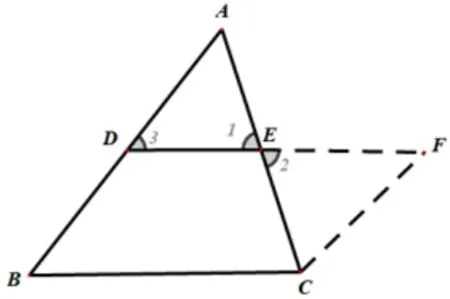
∵AE=CE,∠1=∠2,

∴ΔABC∽=ΔCDA(SAS),

∴∠3=∠F,AD=CF,

∴CF//BD,又∵AD=BD,∴CF=BD,

∴四边形BCFD是平行四边形,∴DF//BC,DF=BC.

∴DE//BC,DE=

3 数学本质三: 中位线定理提供了证明线段平行和线段成倍分关系的根据

对于三角形(这个三条线段围成的闭合图形)内部线段的研究,我们研究的顺序是: 三角形三边(线段两端都在顶点),再到三角形内的特殊线段及中线、高、角平分线(线段一端为顶点,另一端在边上),再到三角形中位线(两端均在边上).中位线定理也就是为“两端均在边上中点”这一特殊情况提供了推理位置关系、数量比例关系的根据.

3.1 基于数学本质的探究活动三: 三角形中位线定理的运用

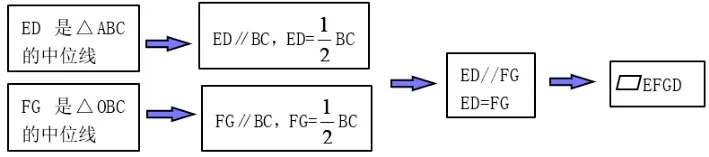
【巩固新知】已知: 如图,在ΔABC中,中线BD、CE相交于O,点F、G分别是OB、OC的中点.求证: 四边形EFGD是平行四边形.

【思路生成】

4 反思与总结

数学知识方面: 学了三角形中位线定理及其运用数学素养方面(四个一): ①一个技能: 证明线段平行和线段成倍分关系的方式根据.②一个方式: 观察、猜想、论证是研究数学问题常用的方法.③一个思想: 转化思想.将三角形的问题转化为平行四边形来解决.④一个道理: 数学问题的对立与统一.研究图形往往从整体(平行四边形)到局部(三角形),也可以由局部(三角形及其中位线)回归整体(平行四边形).

5 .结束语

新课标(2022 版)实施后,对于教师的数学专业素养要求更高了,我们需理清数学内在逻辑,抓住数学本质,才能在零散概念中提炼出核心问题来,共同构成学科的有机整体;才能有效引导学生发现和提出、分析和解决数学问题;才能将有限的、深层次的重要观念进行有意义的联结;才能让学生真正经历深度学习,最终落实学生的核心素养[3].