基于舍选抽样BRDF离散数值的散射光线追迹方法

乔文佑，高志山，袁群，朱丹，许宁晏，伦旭磊，车啸宇

（南京理工大学 电子工程与光电技术学院，南京 210094）

0 引言

在空间相机、卫星激光通信、引力波探测等高精度空间平台光机系统中，杂散光对系统信号的影响是不容忽视的［1-3］。光机系统的元器件是杂散光的重要来源，其表面光散射特性直接影响着系统内杂散光分布情况，针对系统元器件表面散射特性进行光线追迹和杂散光分析，是光学设计及仿真中重要的研究内容。以蒙特卡洛法（Monte Carlo Method，MCM）模拟抽样为基础，基于描述表面散射特性的双向反射分布函数（Bidirectional Reflectance Distribution Function，BRDF）来进行散射光线追迹，是目前科研实验及杂散光分析软件的常用算法。

应用MCM 实现散射光线准确追迹的关键在于由BRDF 模型建立正确的散射光线追迹概率模型，常用的概率模型求解方案主要为反变换法［4］。以反变换法设计概率模型进行光线追迹的方法，主要核心内容：1）选用现有的BRDF 模型解析式对实测BRDF 数据进行拟合解析，选出合理的BRDF 模型；2）将BRDF 转化为概率密度函数（Probability Density Function，PDF），通过求解PDF 的累积分布函数（Cumulative Distribution Function，CDF）的反函数，完成合理采样并以此确定散射光线方向，最终实现光线追迹。然而，系统元器件表面由于其微观形貌特点和纹理分布的特殊性，表面散射特性显示出复杂多样化，且伴随加工技术创新及新材料表面的出现，商用软件包内建的或现有的BRDF 模型或相关修正模型，可用于精确表征表面散射属性的模型种类有限。BRDF 模型参数解析过程繁杂，存在拟合误差，模型适用条件存在限制等问题［5-6］。同时，反变换法虽然可高效产生服从指定分布的随机样本，但是多数散射模型的BRDF 受光线坐标变量θ与φ调制，在复杂概率模型设计过程中，对形式复杂的PDF，其CDF 存在无解析解的情况，反变换法失效［7］。

针对以上问题，为简化表面散射特性的建模分析过程，增强散射光线追迹方法的适用性，本文提出了一种直接使用散射表面BRDF 离散数值的散射光线追迹方法。对随散射角离散变化的各向同性散射表面BRDF 离散测量数据组，由散射角半球空间转换到方向余弦空间，通过等间距赋值插等值方式，得到方向余弦空间内完整分布的BRDF 数据。利用舍选抽样法不受限于CDF 求解过程的优点，设计新的散射概率模型，即计算方向余弦空间内BRDF 数值比表示离散光线的概率分布，设定检验条件筛选出散射光线空间坐标，实现散射光线追迹。

1 理论基础

1.1 双向反射分布函数表征模型

双向散射分布函数（Bidirectional Scattering Distribution Function，BSDF）是描述材料表面对入射光在半球空间内散射情况的度量函数［8］，表征结构表面散射特性，被广泛应用于光学遥感等测量领域［2，9］。BSDF 实际包括反射和透射两个部分，如对透射部分的散射光感兴趣，需要定义双向透射分布函数（Bidirectional Transmittance Distribution Function，BTDF）。因篇幅有限，不失一般性，以表面散射光线追迹算法为例，讨论与反射部分BRDF 有关的散射光线追迹方法，方法同样适用于透射情形。BRDF 被定义为空间某一散射方向光线的辐射亮度与入射光照在材料表面上的辐射照度比值，即

式中，光线入射角由θi与φi两个分量表示，分别为入射光线的天顶角与方位角；散射光线的散射角也由θs与φs两个分量表示，分别为散射光线天顶角与方位角；dLs(θi，φi，θs，φs)为散射方向的辐射亮度；dEi(θi，φi)为入射方向的辐射照度，物理模型如图1 所示。

图1 BRDF 物理模型Fig.1 BRDF physical model

自然界中，具有各向同性散射特征的表面是普遍存在的，工程应用中，加工工艺决定了光机系统的很多介质表面散射可近似看作是各向同性的，对此类介质表面散射特性表征的经典BRDF 模型有ABg 模型［5］、Harvey 模型［10］等。该类模型解析式中，可将变量(θi，φi，θs，φs)转换成变量为R的函数，

式中，ri与rs分别为入射光线与散射光线在方向余弦x-y坐标系中投影单位向量，如图1 所示。xi和yi与xs和ys分别为入射光与散射光在方向余弦坐标系中的坐标，其中xi=sinθicosφi，yi=sinθisinφi，xs=sinθscosφs，ys=sinθssinφs，即为半球空间内光线的天顶角与方位角在方向余弦空间的变量关系。在方向余弦空间（x-y坐标系）中，光线映射成点，与镜像反射光线映射点等间距位置的BRDF 数值始终相等。可根据入射光线和镜像反射光线映射点所在平面（如图2 方框切面xs=0）内的BRDF 数据，通过等间距赋值插等值方式，得到散射表面在方向余弦空间内完整分布的BRDF 数据，即散射角半球空间内任意散射角度光线的BRDF 值。

图2 方向余弦空间介质表面BRDF 数值分布Fig.2 Cosine-space BRDF distribution on medium surface

1.2 基于蒙特卡洛-舍选抽样法的光线追迹模型

蒙特卡洛法（MCM）是一种随机统计的概率模拟方法，其思想是通过对随机变量进行统计试验，进而求得近似解的数值方法［11］。在杂光分析仿真中，MCM 是非序列光线追迹的基础算法，对光线在系统传播过程出现的散射等问题，通常采取构建散射光线分布的概率模型，将光线的空间坐标作为抽样对象，经过模拟抽样确定散射光线方向，实现散射能量在空间分布，转变为携带等能量的离散光线分布，以散射空间光线密度表征能量分布，最终完成散射光线追迹［12］。

如前所述，基于MCM 实现散射光线追迹的关键，在于对其概率模型的正确构建，而概率模型求解方法常使用反变换法，但反变换法时常失效［7，13］。对于已知光机表面BRDF 离散实测数据的情形，可以舍弃由实测数据经模型拟合、PDF 和CDF 获取、求解CDF 的反函数等复杂繁琐的技术途径，引入舍选抽样法，直接应用BRDF 离散实测数据组，得到用于散射光线追迹的光线抽样概率函数。

舍选抽样法也称为拒绝采样法［14］，旨在由简单样本完成对复杂样本的抽样。以一维函数为例，设由BRDF 实测数据获取的PDF 函数记为P(x)，通过建立检验条件，对产生的随机数样本完成服从P(x)分布的舍选抽样，具有采样灵活、操作方便等优点。舍选抽样法既可以用于连续分布对象，也可以用于离散分布对象，以舍选抽样法设计概率模型时对多维等复杂数学分布对象同样适用。如图3，舍选抽样时，会选取密度函数c⋅M(x)，c⋅M(x)也被称为挤压函数，使得c⋅M(x)能够覆盖待抽样对象的密度函数 ，其中c为拒绝常数且通常取c=max {M(x)/P(x)}。为保证高效的抽样效率，选取的c⋅M(x)应尽量贴近P(x)曲线且表达式简单。

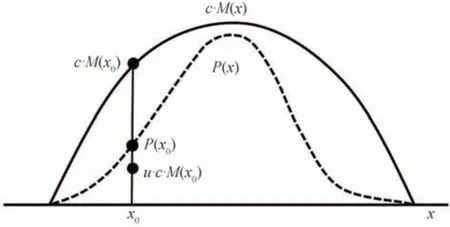
图3 舍选抽样模型Fig.3 Rejection sampling model

舍选抽样过程中，首先生成密度函数为c⋅M(x)的一个伪随机数x0，再从均匀分布（0，1）中产生一个伪随机数u，当u满足关系式（3）检验条件时，x0为接受样本，否则拒绝，重新生成随机数。重复以上过程，即可得到许多概率密度为P(x)的伪随机数，最终完成对样本x的抽样。

舍选抽样算法的抽样效率η，实则为c⋅M(x)的样本被接受成为P(x)的样本的概率，即有

可见，抽样效率由选取的函数c⋅M(x)与P(x)共同决定，两者越贴近，抽样效率越大。若c⋅M(x)函数在极小值处，存在函数值与P(x)最贴近，抽样效率最大，若c⋅M(x)函数在极大值处，存在函数值与P(x)最贴近，抽样效率最大。当函数c⋅M(x)越接近P(x)，舍选抽样的效率越高，但相应的抽样难度也越来越大。由于P(x)形式复杂多样，若一一选取贴合度高的挤压函数，不仅选取困难且对其他形式分布的抽样对象存在适用性问题。为了降低抽样难度及提升通用性，对函数c⋅M(x)取常数Z处理，一般Z值可取P(x)的最大值，即

对于常数Z的处理方式，虽然在一定程度上降低了抽样效率，但可以做到对任意分布形式的P(x)函数，都可进行模拟抽样，同时规避了反变换法过程中积分求解难题，通用性好。

接下来，需要解决的问题是，如何从半球空间内任意散射角度光线的BRDF 值（由BRDF 离散测量值得到）产生密度函数P(x)。从概率论角度看，密度函数P(x)的本质，是描述随机变量的输出值在某个确定的取值点附近的可能性。因此，最简捷的产生方法，是将方向余弦空间内的个体BRDF 离散数值与总体BRDF 离散数值总和的比值，作为表征各抽样点相应密度函数值P(x)。对于二维情况，由BRDF 实测数据计算的P(xi，yj)表达式如式（6）。

式中，设定方向余弦空间BRDF 的变量(xi，yj)取随机数，即为待舍选的抽样样本，且需要满足x2i+yj2≤1。 此时，Z=max(P(xi，yj))，式（3）改写为u⋅max(P(xi，yj))≤P(xi，yj)，则在舍选抽样过程中，检验条件“u⋅max(P(xi，yj))≤P(x∗i，yj∗)且(x∗i)2+(yj∗)2≤1”对样本(x∗i，yj∗) 进行舍选，完成服从P(xi，yj)分布的抽样，以此来确定散射光线方向，为直接利用BRDF 离散数值的散射光线追迹方法奠定基础，算法流程如图4 所示。

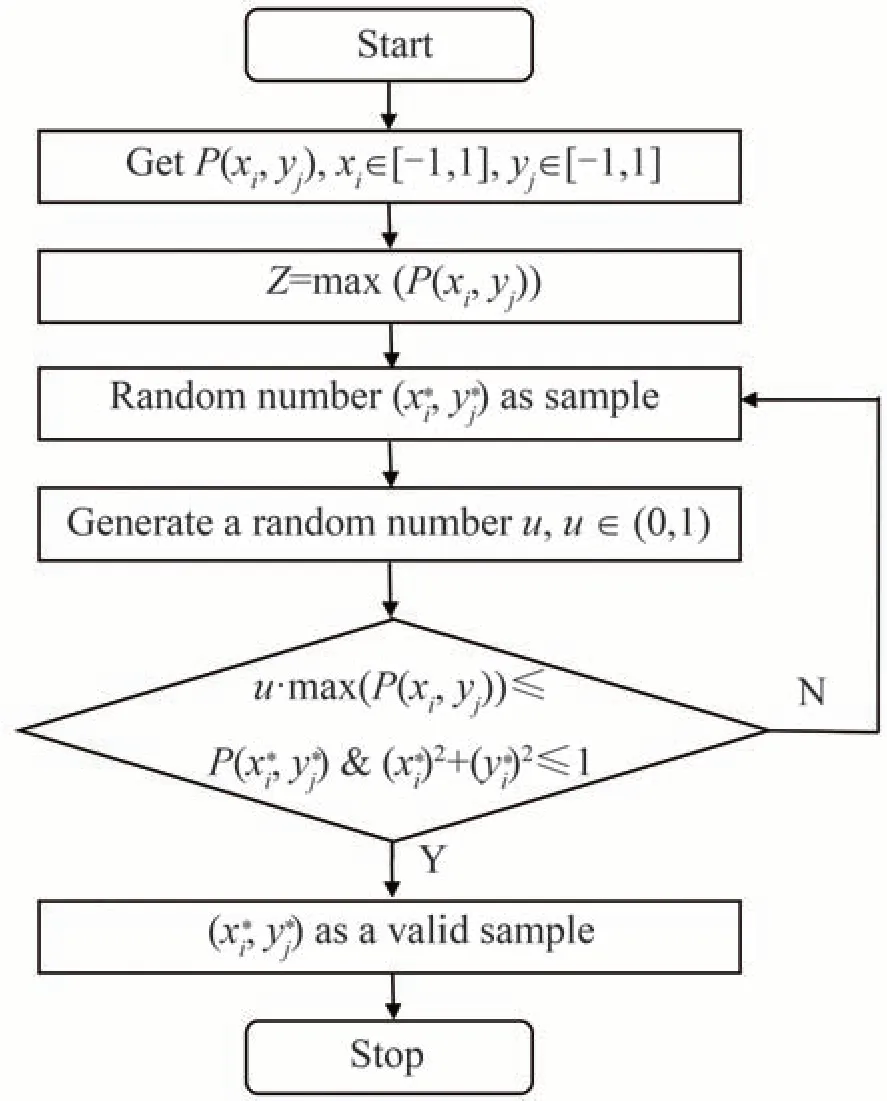
图4 舍选抽样算法流程Fig.4 Flow chart of rejection sampling method

2 仿真验证

2.1 仿真设置

为验证基于舍选抽样BRDF 离散数值的散射光线追迹方法的准确性，设置相同的入射角、追迹光线数量等仿真参数，利用Matlab编写了本文光线追迹仿真程序，并选择与商用软件LightTools相同的概率分光原理设计概率模型［7］，获取散射光线追迹结果的数据群，与相同条件的LightTools软件散射光线计算结果进行比对。

不失一般性，为了方便与LightTools 软件结果的比对，光机表面BRDF 的离散实测值，应选择LightTools 软件中具有的内建光机表面模型，在相同入射角、追迹光线数量情况下，通过对散射角离散获得BRDF 数值，即获取其半球空间中入射光线与镜像反射光线所在平面内的BRDF 离散测量数据，作为本文方法Matlab 追迹程序中散射表面BRDF 实测值。

Harvey 模型是光机表面BRDF 建模的常用散射模型，常用于表征粗糙度在纳米量级的光学表面散射特性，式（7）为Harvey 模型BRDF 表达式。在LightTools 中设置Harvey 散射表面属性，可以表征不同光机表面的模型参数，构建光线追迹仿真系统。

仿真中，对于反射镜表面，Harvey 模型参数为b0=2.43，L=1.8×10−2，s=−2.32［15］；以及Harvey 模型参数为b0=1.185×10−2，L=3.10×10−2，s=−1.9［16］的光学面，仿真设置入射光线能量为1 W，追迹光线数为107，散射能量分析面为边长0.5 mm 的正方形，界面内网格数为100×100，图5 为LightTools 中散射几何空间仿真示意图，表1 为仿真元件的空间坐标。

表1 仿真系统坐标Table 1 Simulation system coordinates

图5 散射仿真系统Fig.5 Scattering simulation system

2.2 验证分析

基于Harvey 模型，按照2.1 所述参数设置方法，构建散射光线追迹仿真系统，仿真结果能量分布如图6所示，其中（a）为本文方法Matlab 追迹程序的计算结果，（b）为LightTools 软件的计算结果。

图6 Harvey 仿真模型散射能量分布图，b0=1.185×10−2，L=3.10×10−2，s=−1.9Fig.6 Scattering energy distribution of Harvey simulation model， b0=1.185×10−2，L=3.10×10−2，s=−1.9

由图6 可以看出，仿真结果是与追迹光线数量匹配的数据群，数据量较大。为对比仿真结果的偏差，本文引入了通用质量指数（Universal Quality Index， UQI）。UQI 是通用的图像质量多元素同步评价指标，其定义包含了相关性损失、亮度失真和对比度失真三个元素［17］，可以量化图像之间的相对失真程度。因为成像本质与能量分布相关，因此，本文采用UQI 作为仿真结果相似性的评价值，通过计算UQI 来量化散射能量分布的相似度。UQI 表达式为

由于蒙特卡洛模拟过程中采样具有随机性，造成连续散射光线追迹仿真结果并不完全相同，为验证仿真的精确度，对上述Harvey 模型及参数进行了多次同步仿真。通过观察Matlab 追迹程序第n次与LightTools 第n次仿真散射能量之间的UQI 值动态范围，验证本文光线追迹方法的合理性。

图7 为不同Harvey 散射模型参数表征的材料表面散射光线追迹仿真结果，对每种参数模型分别进行了10 次关于本文光线追迹方法与LightTools 同步仿真对比。可见，本文光线追迹方法与LightTools 同步仿真结果的UQI 值动态范围分别在0.999 4～0.999 5 和0.999 2～0.999 3 区间，且UQI 值的波动范围小，说明本文光线追迹方法与LightTools 仿真得到的散射能量分布高度一致，因此，本文基于舍选抽样BRDF 离散数值的散射光线追迹方法具有较高地准确度与稳定度。对于不同材料表面散射仿真结果评价的UQI 值出现的差异，是由BRDF 模型种类及其模型参数决定。

图7 Harvey 模型仿真UQI 动态范围Fig.7 The UQI range of Harvey model simulation

为了进一步验证本文基于舍选抽样BRDF 离散数值的散射光线追迹方法的适用性，同上述仿真对比过程，选择能够对大量光机结构表面建模的ABg 模型。其中，选择了用于表征材质为BK7 平凸型准直物镜［18］表面散射特性和发黑铝合金［5］表面散射特性的ABg 模型参数，进行多次同步光线追迹仿真实验，模型参数见表2。

表2 仿真系统坐标Table 2 Simulation system coordinates

不同参数的ABg 模型所表征的材料表面散射光线追迹仿真结果如图8 所示。可见，本文光线追迹方法与LightTools 同步仿真结果的UQI 值动态范围分别在0.999 0～0.999 1 和0.998 7～0.998 8 区间，UQI 值的波动范围小，说明两者仿真所得到的散射能量分布高度一致，本文基于舍选抽样BRDF 离散数值的散射光线追迹方法不仅准确度高，对不同表面散射特性的表征同样具有良好地适用性。

图8 ABg 模型仿真UQI 动态范围Fig.8 The UQI range of ABg model simulation

2.3 复合散射表面应用

由于系统元器件或涂层表面微观形貌特点和纹理分布的特殊性，其表面散射呈现复杂多样化，单一BRDF 解析模型很难对测定的散射数据进行高精度拟合，通常需要多个BRDF 解析模型进行复合拟合，并确定各BRDF 模型的权重系数，复合BRDF 模型如式（9）所示。

式中，BRDF1、BRDF2分别为各种类BRDF 模型，k1、k2分别为各类BRDF 模型的权重系数。

为验证本文基于舍选抽样BRDF 离散数值的散射光线追迹方法对复合散射表面光线追迹的适用性，在LightTools 软件中构建了包含朗伯散射与高斯散射的复合散射表面光线追迹模型。其中，朗伯散射模型表达式为

式中，ρ为总反射比。

高斯散射模型表达式为

式中，K为归一化常数，，σx与σy为高斯分布的标准差。

LightTools 仿真模型中设置朗伯散射与高斯散射的权重系数k1与k2分别为0.3 与0.7，朗伯散射的总反射比ρ为1，高斯散射分布的标准差σx与σy均为15°。通过以上复合BRDF 模型及参数，获取其半球空间中入射光线与镜像反射光线所在平面内的BRDF 离散测量数据，作为本文方法Matlab 追迹程序中散射表面BRDF 实测值，利用Matlab 追迹程序与LightTools 软件进行多次同步仿真对比。

图9 为复合散射表面基于本文光线追迹方法与LightTools 软件建模进行10 次同步仿真对比结果。可见，本文光线追迹方法与LightTools 同步仿真结果的UQI 值动态范围在0.998 8～0.998 9 区间，UQI 值的波动范围小，说明两者仿真得到的散射能量分布高度一致。因此，本文基于舍选抽样BRDF 离散数值的散射光线追迹方法对于复合散射表面的光线追迹同样具有良好的适用性。

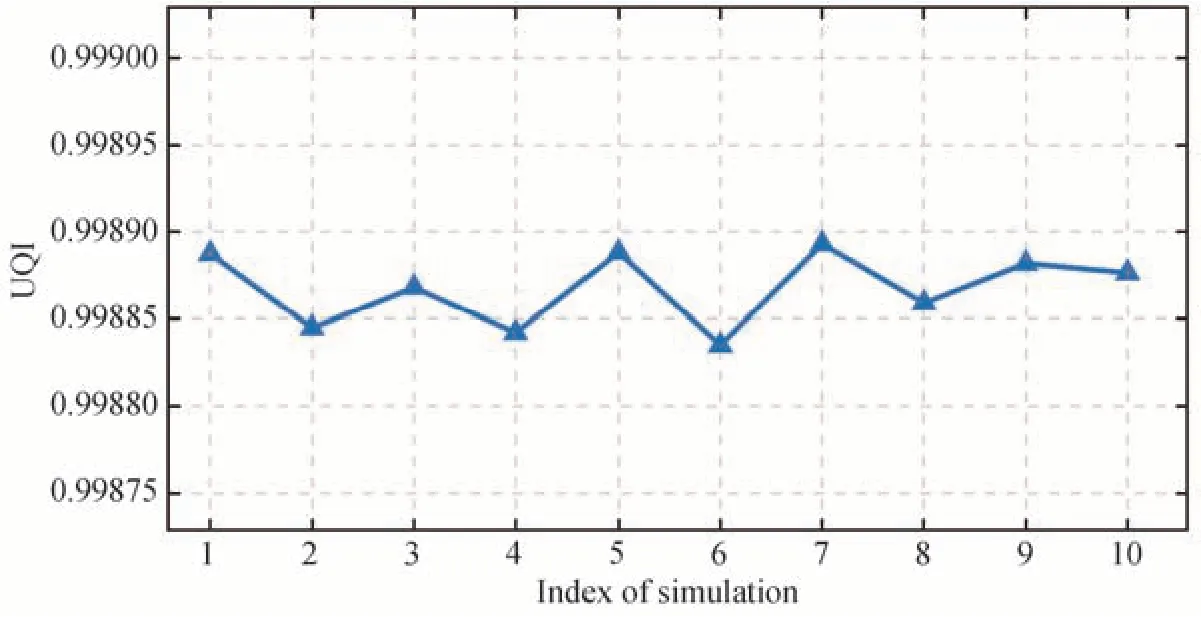
图9 复合散射表面模型仿真UQI 动态范围Fig.9 The UQI range of ABg model simulation

相较于LightTools 软件无法直接构建介质表面为Harvey、ABg、高斯等复杂的复合散射表面仿真模型，本文提出的基于舍选抽样BRDF 离散数值的散射光线追迹方法具有良好的光学仿真优势，可以准确、便捷地完成此类复杂的复合散射表面光线追迹。

3 结论

为简化表面散射特性建模分析过程，增强散射光线追迹方法的适用性，本文提出了一种直接使用散射表面BRDF 离散数值的散射光线追迹方法。基于蒙特卡洛法模拟散射光线分布思想，以方向余弦空间内BRDF 数值比表示离散光线的概率分布，结合舍选抽样法筛选出散射光线的空间坐标，实现散射光线追迹。该方法不仅避免了对BRDF 模型选用的繁杂过程，同时也规避了反变换法过程中积分求解难题。为了验证本文光线追迹方法的准确性与适用性，在相同入射角、追迹光线数量情况下，选用光学软件LightTools 设置表征各类光机元器件表面散射特性的Harvey、ABg 以及复合散射表面的BRDF 模型及参数，进行建模仿真。利用Matlab 编制本文光线追迹方法的仿真程序，通过LightTools 设置的BRDF 模型及参数，获取其半球空间中入射光线与镜像反射光线所在平面内的BRDF 离散测量数据，作为本文方法Matlab 追迹程序中散射表面BRDF 离散实测值，进行同步光线追迹仿真。采用UQI 作为LightTools 软件仿真与本文光线追迹方法仿真结果比对的评价值。结果显示，UQI 值均在0.998 以上且波动范围小，说明本文基于舍选抽样BRDF 离散数值的散射光线追迹方法准确度高且具有良好地适用性。随着加工制造技术和光学涂层工艺的不断更新，为满足精密光学系统研制中对新型机械加工材料和涂层表面散射特性的分析工作，本文散射表面光线追迹方法可为此项工作提供一种简捷准确地分析途径与思路，具有重要的实际应用和推广价值。