水翼空化流场的调控和优化研究
2023-06-15赵伟刘真威陈石阳丁耀东李平
赵伟,刘真威,陈石阳,丁耀东,李平
(西安交通大学热流科学与工程教育部重点实验室,710049,西安)
在水力机械运行过程中,当局部压力降低为饱和蒸汽压时,液相变为气相产生空化。空化会在叶轮旋转过程中周期性生成和溃灭,引起水力机械的振动和噪声[1-2]。空化溃灭时形成的冲击波会对设备表面产生高度集中的表面应力,附着型空化的周期性脱落与不稳定流动会导致表面应力的反复作用,造成表面材料的侵蚀,影响设备的安全运行[3-4]。因此,改善空化流场,抑制和削弱空化对水力机械产生的破坏,对于提高效率、保持水力机械安全稳定的运行至关重要。
NACA翼型在水力机械中获得大量应用,但NACA翼型的开发主要以飞机机翼为应用目标,没有考虑空化问题。因此,在保持水动力性能的基础上,有必要设计符合水力机械抗汽蚀性能的NACA翼型。常欣等[5]对三维水翼型线进行了优化设计,优化后翼型前缘厚度减小并呈流线型,水翼升阻比提高。黄胜等[6]利用多目标优化算法,以提高升阻比和改善水翼表面压力分布为优化目标,对不同翼型的型线进行了改进,改进后水翼的厚度减小,升力效率和空泡性能提高。黄斌等[7]利用粒子群优化算法对NACA66(MOD)水翼型线进行了改进,获得的最优方案中,最大拱度位置向尾缘移动,最大厚度略微增加。李靖璐等[8]采用自由变形法对NACA0012水翼进行了型线调整,研究发现,水翼厚度减小可使阻力系数降低,后缘扭转可使升力系数增加。Luo等[9]利用NSGA-Ⅱ算法对水轮机叶片翼型进行了优化设计,改进后水翼前缘附近的曲率半径增大,翼型厚度减小,升阻比和最小压力系数增加,运行效率提高,减小了空化发生的可能性。上述研究结果表明,改进水翼型线可以实现空化流场的整体调控,并改善水翼的水动力性能。
以流场中空化发生的局部位置及后续发展趋势为着眼点,其调控方法主要有主动式控制和被动式控制。被动控制方法中,布设流动控制结构是一种易于实施和维护的控制方式。Kadivar等[10]在水翼表面分别布置了圆柱形和半球形涡发生器,研究发现在合适位置布置涡发生器可以抑制空泡脱落,减小水翼尾迹区的压力脉动。顾魏等[11]分别在35%弦长和75%弦长位置处布置单个展向挡流条,发现35%弦长处的挡流条在一定的空化数范围内增强了空化的稳定性。Qiu等[12]在NACA0015水翼表面布置微涡发生器,发现微涡发生器对流体进行扰动,促进了不同能量流体的混合,形成稳定的涡流区,使空泡破灭时剧烈程度降低,减小了对水翼表面的空蚀。以上研究表明,流动控制结构可以实现局部空化流场的有效控制。在空化范围较大时,单个结构的控制作用有限,因此连续流动控制结构成为了优选方法[13-15]。
在布设多个流动控制结构时,其几何参数和相对位置会显著影响空化控制效果,而将优化算法耦合到数值求解和参数化分析过程中,则可以快速得到理想的控制结构参数。Lin等[16]将简化的共轭梯度法与数值模拟方法相结合,对微通道中肋的宽度和厚度等结构参数进行了优化设计,获得不同工况下最优设计变量组合。Mazaheri等[17]利用差分进化优化算法对翼型表面的凸起结构进行了优化设计,优化后的翼型阻力和流动分离区域减小,增强了流场的稳定性。Xue等[18]利用遗传算法对凹槽结构的数量和深度等进行了全局优化,获得的最优凹槽结构改善了凹槽区域的压力分布,抑制了空化的产生。以上研究表明,耦合优化算法能够为空化性能和水动力性能的优化提升提供有效的快速实现方法。
综上分析:本文通过改进水翼型线,进行空化流场的整体优化;通过布设连续流动控制结构,并基于广义模式搜索算法进行结构优化,快速实现空化流场的局部精准调控。
1 数值计算方法
1.1 物理模型和边界条件
在水翼空化流场研究中,本文选择NACA0009、NACA0012和Clark Y 3种典型水翼型线进行对比分析。NACA0009和NACA0012为低速对称翼型,弯度均为0,具有低阻力系数,是水力机械中的基础翼型;Clark Y水翼为非对称翼型,具有高升力系数。图1展示了NACA0009、NACA0012和Clark Y 3种水翼型线的对比,3种水翼弦长相等,均为0.1 m。其中,NACA0009水翼最大厚度为9.90 mm,位于49.5%弦长处;NACA0012水翼最大厚度为12.0 mm,位于30%弦长处;Clark Y水翼最大厚度为11.7 mm,位于28%弦长处,吸力面最大凸起高度为9.16 mm,位于36%弦长处,最大弯度位于42%弦长处。
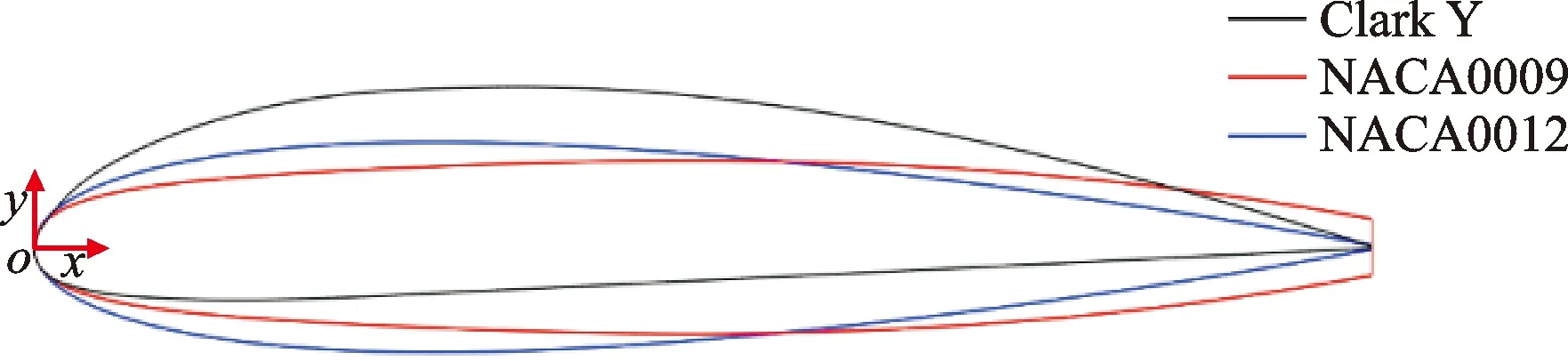
图1 3种水翼型线对比
计算域如图2所示,采用速度入口和静压出口,水翼表面和上下壁面为无滑移壁面。流体温度为20℃,在此条件下饱和蒸汽压为2 300 Pa,水的密度为998 kg·m-3,蒸汽密度为0.017 kg·m-3,水的动力黏度为0.001 kg·m-1·s-1,蒸汽动力黏度为9.60×10-6kg·m-1·s-1。在入口速度为10 m·s-1条件下,针对攻角为6°和8°,空化数为1.5、1.3、1.0和0.8等工况时,对比分析不同水翼的流场特性。
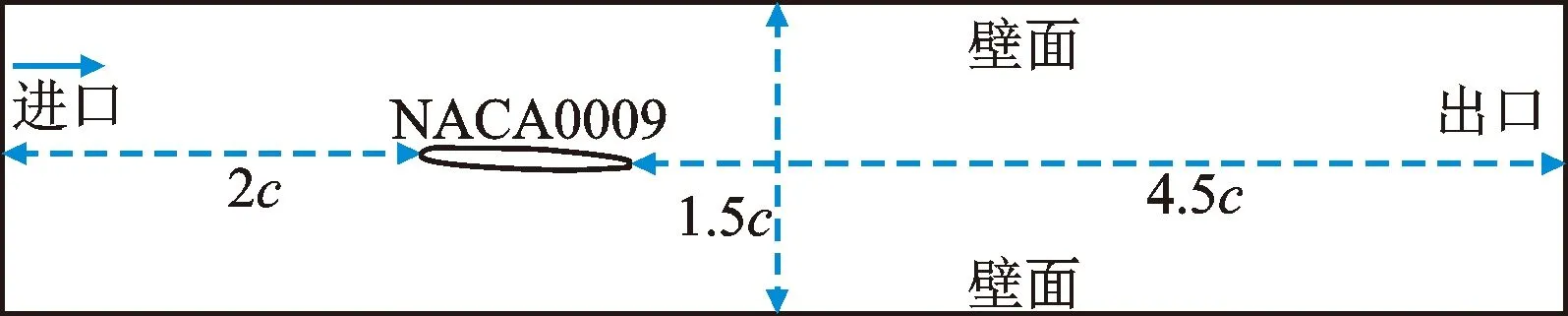
图2 水翼空化模型计算域
1.2 数值计算方法
1.2.1 基本控制方程
本文研究采用均质混合流模型[19],其中液相和气相具有相同的速度和压力,空化流动非稳态求解控制方程如下。
混合相的连续性方程为

(1)
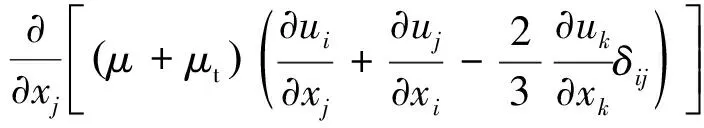
(2)
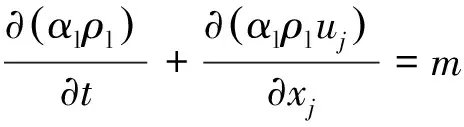
(3)
其中混合相的密度和黏度分别为
ρ=αvρv+ρl(1-αv)
(4)
μ=αvμv+μl(1-αv)
(5)
式中:ρ为混合相密度;ui(i=1,2,3)表示与坐标轴xi平行的速度分量;αv为气相体积分数;下标l代表液相,下标v代表气相;m为两相之间的传质速率。
1.2.2 湍流模型
本文采用剪切应力输运(SSTk-ω)湍流模型[20]对空化流动进行计算,该模型如下
(6)
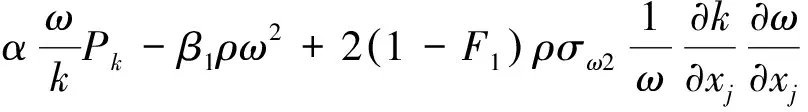
(7)
式中:k为湍动能;Pk为湍流产生率;ω为湍流频率;σk=0.85;σω1=0.5;σω2=0.856;F1为混合函数。
由于原始的SSTk-ω模型过度预测了空化区域的湍流黏度,因此Ducoin等[21]对SSTk-ω模型进行了修正,考虑了混合相局部可压缩性的影响,提出了基于局部气相体积分数的混合湍流黏度求解方法,将原公式中的湍流黏度μt修正为
μt_mod=μtf(ρ)
(8)
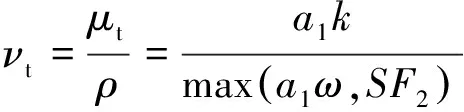
(9)
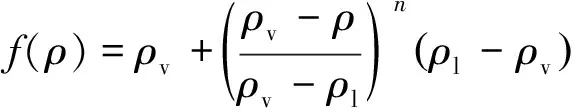
(10)
式中:a1=0.31;S为液体表面张力系数;F2为混合函数。通过调节n降低空化区域的密度,从而减小湍流黏度,参照文献[21-22],当n取3时,对空化区域湍流黏度的预测满足本研究的精确度要求。
1.2.3 空化模型
Zwart空化模型在非稳态空化模拟中具有较好的效果,自提出至今,进行了大量验证[23]。考虑Rayleigh-Plesset方程的二阶项对空化数值模拟的影响,Geng等[24]通过数学推导对Zwart空化模型进行了修正,得到更接近实验的计算结果,修正后的空化模型为

(11)
式中:me为蒸发传质速率;mc为冷凝传质速率;αnuc为汽核体积分数,取5×10-4;R为1×10-6m;Fcond为凝结系数,取0.01;Fvap为汽化系数,取50。
1.2.4 参数定义
空化数σ是描述空化状态的无量纲参数,其定义为
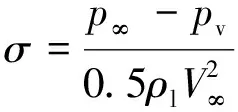
(12)
式中:p∞为出口压力;V∞为来流速度。
压力系数定义为
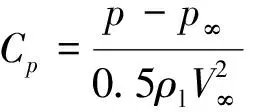
(13)
反映水翼水力特性的升力系数、阻力系数分别定义为
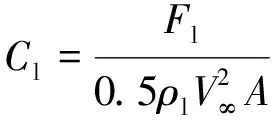
(14)

(15)
式中:Fl、Fd分别为水翼所受的升力和阻力;A为翼型投影面积,二维翼型时为翼型弦长。
1.3 模型验证
1.3.1 网格无关性验证
本文中对流体域进行结构化网格划分,并对水翼近壁区进行网格加密,调整第一层网格高度,确保离壁面最近的第一个点位于黏性底层内,基于下式保证y+<1,网格划分如图3所示。

图3 水翼周围及两端网格示意图
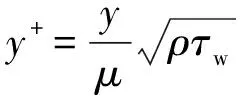
(16)
式中:y为单元中心到壁面的距离;τw为壁面切应力。
为确定合理的网格数,对网格进行无关性检验,保持第一层网格高度和增长率不变,不断对网格进行加密,最终网格数分别为66 048、94 748和119 608。以升力系数、阻力系数作为评价标准,结果见表1。网格3与网格2相比,参数相对误差均低于0.1%,因此,以网格3为基准,进行后续水翼网格的划分。

表1 网格无关性验证
1.3.2 数值模型验证
以稳态空化流场计算结果作为初始值,对非稳态空化流场进行计算。将NACA0009水翼在入口速度为20 m/s、攻角为2.5°、空化数为0.9时,吸力面压力系数的计算值与Dupont[25]的实验数据进行对比,验证结果如图4所示,可以看出,时均压力系数与实验值吻合较好。
图5给出了Clark Y水翼在入口速度为10 m/s、攻角为8°、空化数为0.8时,计算所得空泡形态随时间的变化及其与实验结果[26]的对比,数值计算结果清楚地描述了云状空化的产生、发展和脱落的准周期性变化,模拟空泡形态与实验结果吻合度较高。

图5 Clark Y水翼云空化空泡演变
综上可见,本文计算模型可以有效模拟水翼流场及其空化特性,模型精度足够可靠,满足下一步研究需求。
2 水翼空化流场整体调控
2.1 流线分布和水动力性能
图6和图7为不同空化数下,一个周期内空化流场随时间的变化。水翼云空化的发展过程可归纳为:空泡从翼型前缘开始产生,并逐步发展成附着在水翼表面的片状空泡;随着回射流向前缘方向运动,空泡尾端被拉伸,并逐渐脱落;脱落的空泡随流体向翼型尾缘方向移动,随着压力增大,空泡逐渐变小,最后在翼型尾缘附近消失。由于空泡的大量脱落和溃灭,造成压力脉动和冲击,对水翼壁面产生破坏。随着空化数的降低,流场压力降低,附着空泡的长度和厚度增加。最终,空泡发展的长度超过水翼尾缘,变成超空化状态。在相同空化数和不同攻角下,同一时刻空泡形态相似,但较大攻角下的空泡体积略大。
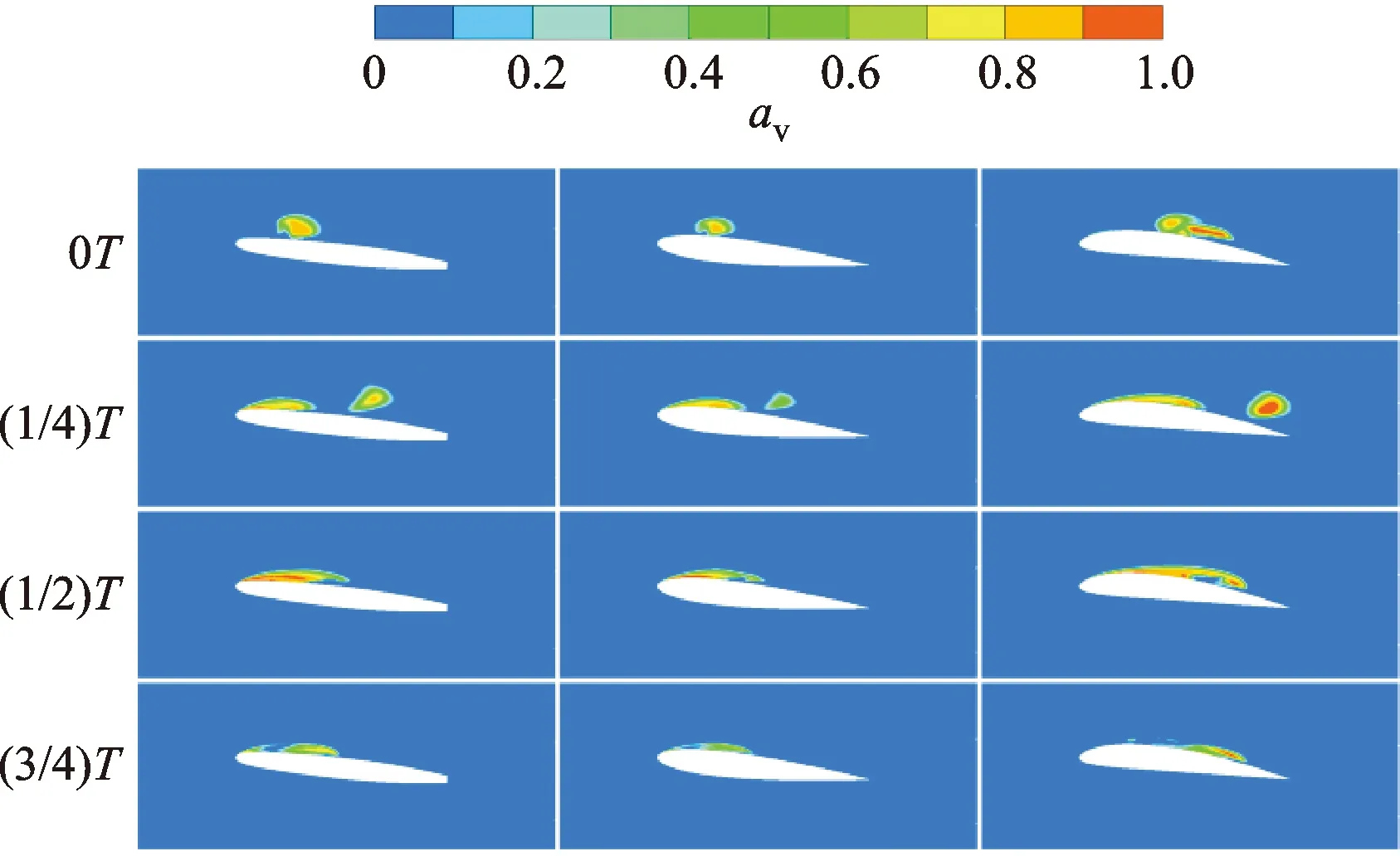
图6 α=6°和σ=1.5时气体体积分数分布

图7 α=6°和σ=0.8时气体体积分数分布
对不同水翼的不同工况进行了计算,图8为不同空化数下各水翼周围的流线分布。空泡区域属于低压区,当水翼表面的附着空化发展到一定程度,由于逆压梯度的存在,流体沿水翼吸力面反方向流动,形成回射流。回射流所在区域速度与主流速度方向相反,对空泡产生反作用,同时与空泡体接触部分不断汽化,在相互作用的过程中,区域整体的运动方向与主流方向相同,形成回射流“倒退”现象。空化数较小时,水翼表面附着空化发展到尾缘附近,导致尾缘吸力面压力降低,与压力面的压差增大,流体从压力面流向吸力面尾缘并形成回射流,因此回射流产生的位置在尾缘附近。空化数较大时,附着空化的长度较小,离尾缘有一定的距离,尾缘附近吸力面和压力面的压差较小,提供给尾缘压力面流体流向吸力面的动力较小,因此尾缘产生的回射流较小。对比不同水翼的回射流分布可以看出,在较小空化数下,NACA0009和NACA0012水翼吸力面尾缘产生的回射流运动的更加深入,而相同空化数下Clark Y水翼吸力面尾缘产生的回射流运动的距离较短。比较3种水翼的型线可以看出,Clark Y水翼吸力面较大的凸起高度,改变了回射流运动的角度,使附着型空化更容易被剪断,从而抑制了回射流向前缘的发展,抑制了空化的发展。因此,在保持吸力面较大凸起高度的条件下,将最大凸起高度位置沿来流方向适当后移,可以抑制回射流的发展,减小空泡的脱落。

图8 α=6°时不同空化数下水翼流线分布
升阻比是评价水力机械水动力性能的重要参数。升阻比越高,意味着效率越高,同样的工作条件下可以节省更多的能源。图9给出了不同工况下3种水翼的升阻比大小。如图9所示,随着空化数的升高,各水翼的升阻比也逐渐升高。仅在攻角为6°、空化数为1.0时,NACA0009水翼升阻比大于Clark Y水翼升阻比,其余工况下Clark Y水翼的水动力性能均优于NACA0009水翼和NACA0012水翼。对于不同水翼,攻角为6°时的升阻比均大于攻角为8°时的升阻比。尽管攻角增大,升力系数也随之增大,但阻力中的诱导阻力增加比重更大,因而最终的结果是升阻比减小。Clark Y水翼的升阻力特性与NACA0012水翼、NACA0012水翼的升阻力特性不同。如表2所示,对于NACA0012水翼,升力系数和阻力系数均小于Clark Y水翼,而阻力系数对升阻比的影响较大。因此,NACA0012水翼和具有高升力系数的Clark Y水翼在升阻比上差别较小。NACA0012水翼具有最小阻力系数,NACA0009水翼的阻力系数介于NACA0012水翼和Clark Y水翼之间。结合图1中3种水翼的型线对比可以得出,翼型吸力面凸起高度过小和过大都会使阻力系数增大。因此,为保持高升力系数的同时拥有较小阻力系数,型线的凸起高度需要介于Clark Y水翼和NACA0012水翼的凸起高度之间。

表2 α=6°的时水翼升力系数、阻力系数
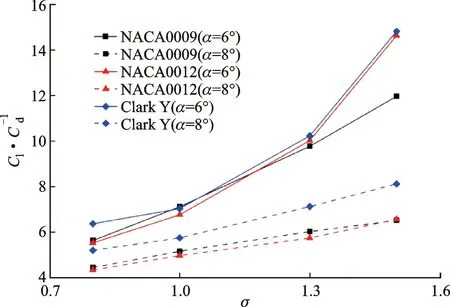
图9 不同工况下的升阻比
2.2 新水翼结构与流场分析
为保证水动力性能的同时,实现对空化的整体调控,本研究依据多项式形式的型线方程设计新水翼型线[27]。在对比分析的3种水翼中,Clark Y水翼综合性能最佳,通过Clark Y水翼的数据点拟合型线方程,确定多项式中的各项系数和幂指数,得到待优化的初始型线方程
y=pxa1(c-x)b1±qxc1(c-x)d1±
rxs1(c-x)t1
(17)
式中:p、q、r均为大于0的常数。对于上下型线,指数a1、b1、c1、d1、s1、t1可以取不同的值,但均为大于0的常数。
基于前文翼型对比分析得出的型线优化思路,以NACA0012水翼和Clark Y水翼型线作为新水翼型线优化的参数变化范围。以改善水翼的空化性能和水动力性能为目标,通过对比不同的常数值,调整型线方程对型线进行优化,进而确立新水翼型线,方程式如下
(18)
式中:ys、yp分别为吸力面、压力面型线方程。由型线方程建立新水翼模型,命名为NF水翼模型。
新水翼型线和现有3种水翼的对比如图10所示。新水翼的最大厚度为11.3 mm,在33%弦长处,吸力面最大凸起高度为8.34 mm,在38.4%弦长处。新水翼吸力面凸起高度介于NACA0012水翼和Clark Y水翼之间,并且与Clark Y翼型相比,吸力面最大凸起高度的位置沿来流方向后移。

图10 新水翼型线示意图
通过翼型优化方案,建立了新的翼型结构。图11展示了不同空化数下新水翼流线分布,可以看出,空化数较小时,回射流从尾缘产生并向前缘流动;空化数较大时,回射流产生的位置提前。与图8各水翼流线分布相比,在相同的空化数下,新水翼吸力面回射流向前缘运动的距离比NACA0009水翼和NACA0012水翼小。虽然新水翼吸力面最大凸起高度小于Clark Y水翼,但新水翼吸力面最大凸起高度向后移动了一定的距离,所以回射流发展的距离相比Clark Y水翼增大不明显。因此,利用优化方案建立的新水翼抑制了回射流的发展,减小了回射流对空泡脱落的影响。
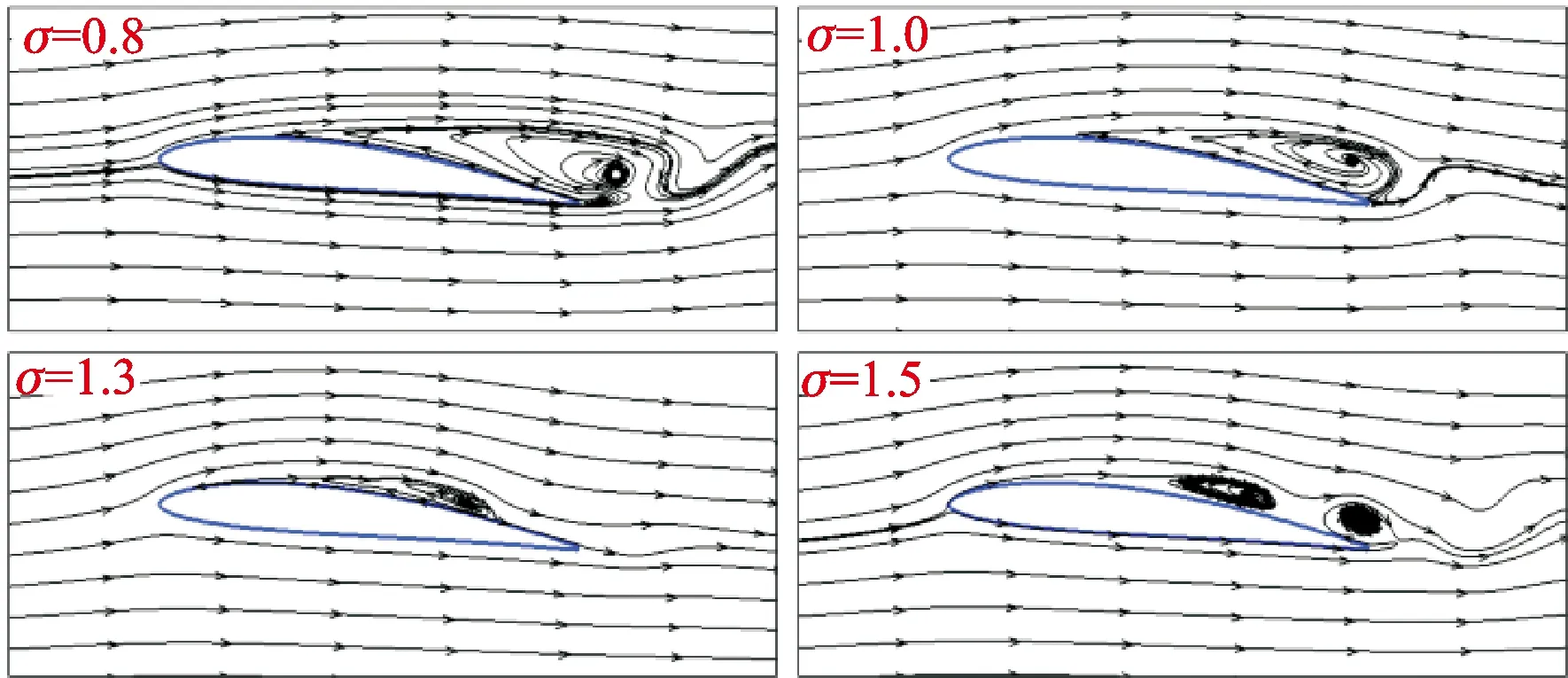
图11 α=6°时不同空化数下新水翼流线分布
新水翼与Clark Y水翼在攻角为6°和8°时的水动力性能如图12所示,可以看出,在相同攻角和相同空化数条件下,新水翼的水动力性能优于Clark Y水翼,升阻比最大提升48.8%。这意味着,根据不同流场特性对比分析得出的型线优化思路,为提高水翼水动力性能提供了方向。新水翼升阻比变化规律与其他3种水翼相同,即升阻比随空化数的升高而升高,且攻角为6°时的升阻比大于攻角为8°时的升阻比。另外,由于新水翼吸力面具有较大的凸起高度,所以新水翼阻力系数较大的同时具有较大的升力系数,升阻比特性与Clark Y水翼类似。

图12 新水翼升阻比特性
3 新水翼流场局部调控
3.1 TR水翼及优化算法
为进一步对新翼型的空化流场进行局部调控,在新水翼上添加流动控制结构。参考空化流场中流动控制结构布置的原则[28-30]可知,控制结构离前缘过近或过远都难以对空化起到有效的控制作用,而控制结构高度过高会对流场产生强烈扰动,对空化造成不良影响。因此,控制结构需选取合适的高度和间距,并且布置在水翼空化覆盖范围内。针对空化区域较大的σ为0.8和1.0两种工况,本文在新水翼吸力面均匀添加3个三角形凸起控制结构,研究多个控制结构对空化流场的影响。新水翼表面添加多个控制结构的模型如图13所示,命名为TR水翼模型。
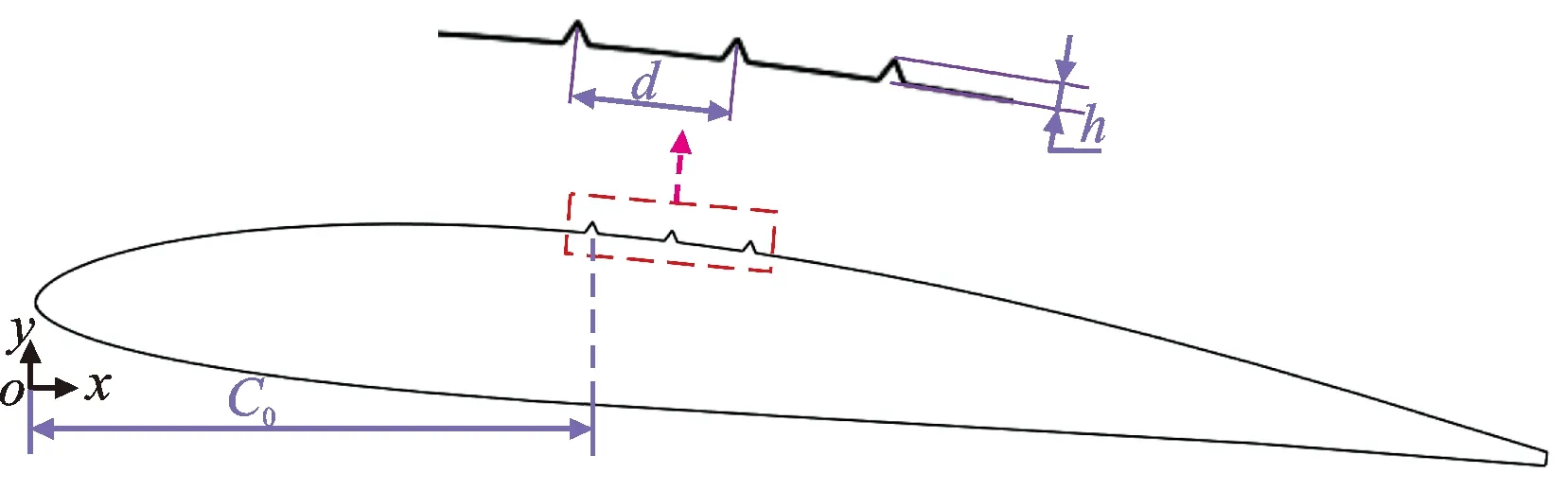
图13 TR水翼模型
利用给定的流动控制结构进行水翼空化调控研究时,存在遗漏流动控制结构最优设计参数的可能。为了实现流动控制结构设计的快速寻优,以及水翼性能的最大化提升,针对TR水翼,利用广义模式搜索算法进行优化设计。在优化过程中,以流动控制结构起始位置C0、控制结构高度h以及相邻控制结构的间距d作为设计变量,以代表水翼水动力性能的升阻比作为目标参数。为保证结构的正常添加,避免远离水翼吸力面前缘,以及控制结构由于间距过小而互相干扰等问题,给出各设计变量[C0,h,d]变化的上下限,对控制结构的添加进行限制,下限为[0.1,0.03,0.003],上限为[0.7,0.3,0.01]。控制结构优化流程如图14所示,利用Matlab调用相应的程序,自动完成几何建模、网格划分以及数值计算,并对结果进行处理。最后,利用Matlab中的优化算法完成目标参数的寻优和对比,并将调整的设计变量参数重新输入,继续下一次迭代。
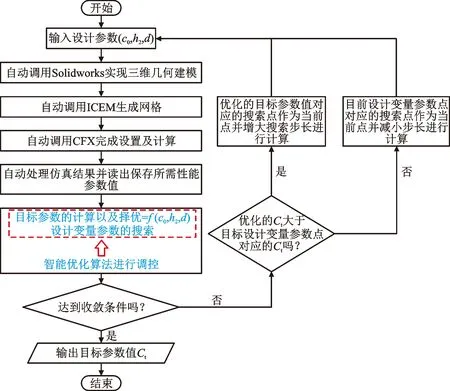
图14 添加控制结构的水翼优化流程图
利用模式搜索算法对函数式(17)进行求解,验证该优化方法的可靠性,得到
f=-x2-2y2+0.4cos(3πx)+
0.6cos(4πy)
(19)
式中:x,y∈[-10,10]。该函数为多峰函数,在[0,0]处具有最大值1。通过模式搜索方法进行最大值搜索,经过多次迭代之后,在x=-0.534 3×10-15,y=-0.104 1×10-15处得到最大值1,两坐标值接近理论值0,由此验证了优化程序的可靠性。
3.2 优化结果与分析
在优化设计中,将攻角为6°和8°时优化前的模型分别命名为TR6和TR8,同时将各工况优化后的模型按照以下规则进行命名:TRα-σ。基于新水翼流场分析结果,综合考虑空泡和回射流产生的位置及大小等,选定本次优化的初始点为x0=[0.025 m,0.000 6 m,0.005 m],即控制结构起始位置C0在弦长25%位置处,控制结构高度h为0.6 mm,相邻控制结构间距d为5 mm。表3为优化前后控制结构参数对比,从优化结果可以看出,优化后流动控制结构初始位置后移,同时控制结构的高度以及间距都增加。
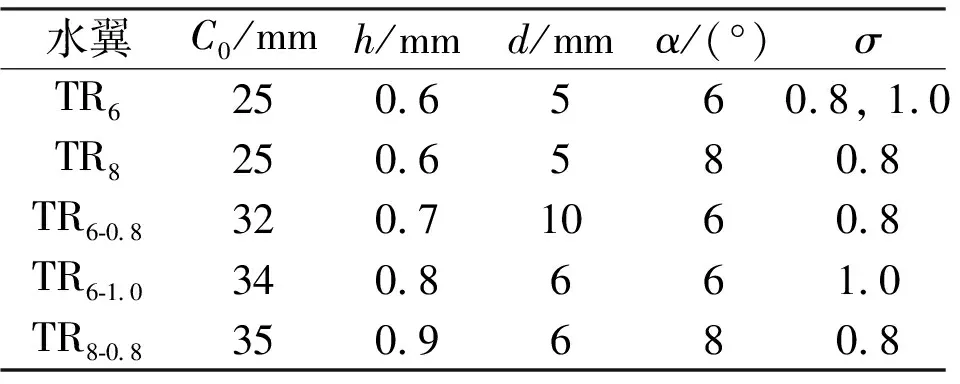
表3 不同工况下流动控制结构优化结果
优化后水翼特性与NF水翼、TR水翼特性的对比如图15和图16所示,可以看出,相对于NF水翼,TR水翼升阻比减小,空化厚度Cy与长度Cx增加。通过优化设计后,水翼的升阻比增加,与NF水翼相比,TR6-0.8水翼升阻比提升了9.5%,TR6-1.0水翼升阻比提升了13.6%,TR8-0.8水翼升阻比提升了4.8%。同时,优化后水翼空化的发展得到了抑制,空化长度Cx与厚度Cy均有所减小。这意味着,使用优化设计程序实现了流动控制结构的优化,空化流场得到局部调控。
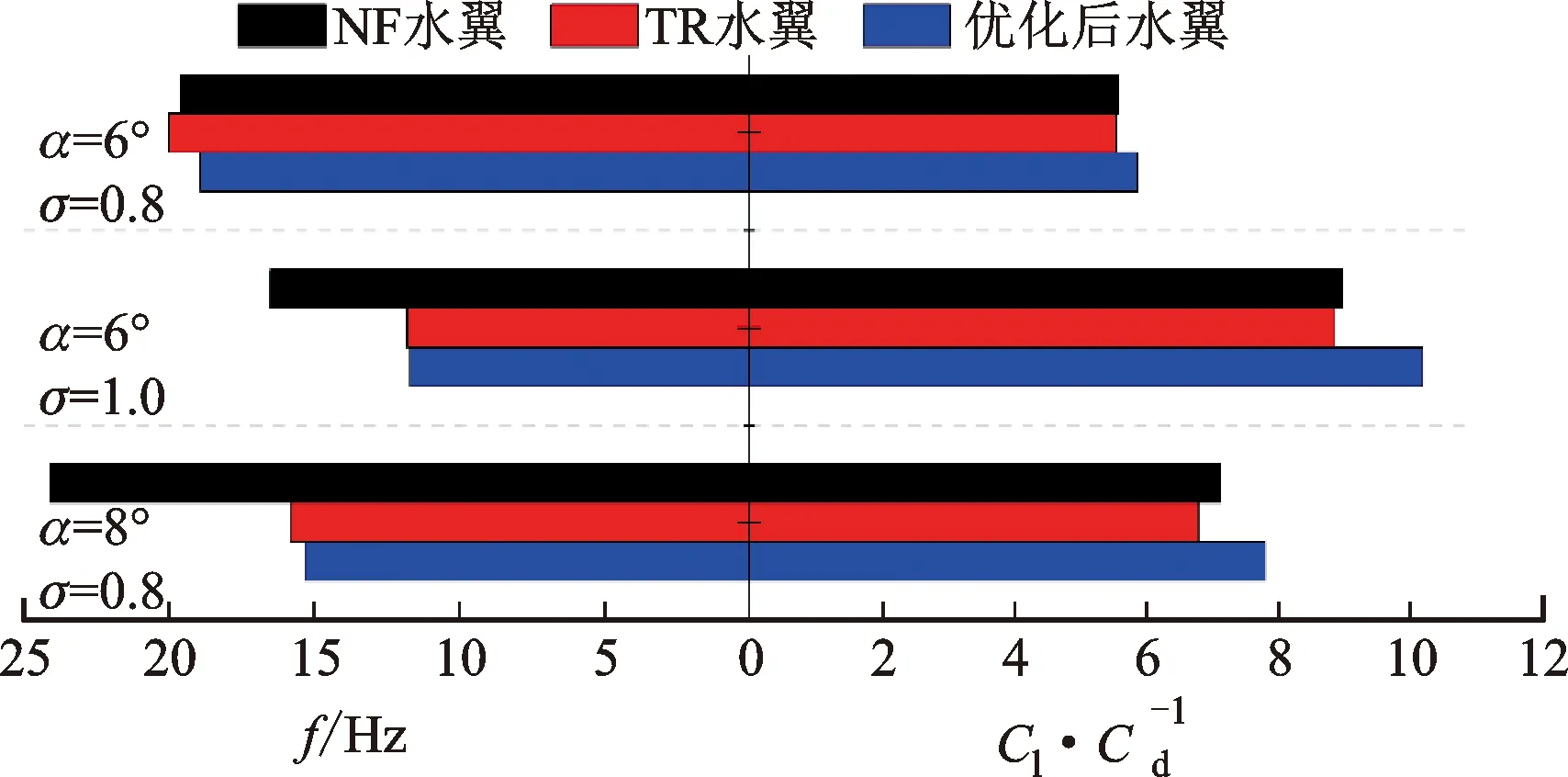
图15 优化前后水翼空泡脱落频率和升阻比
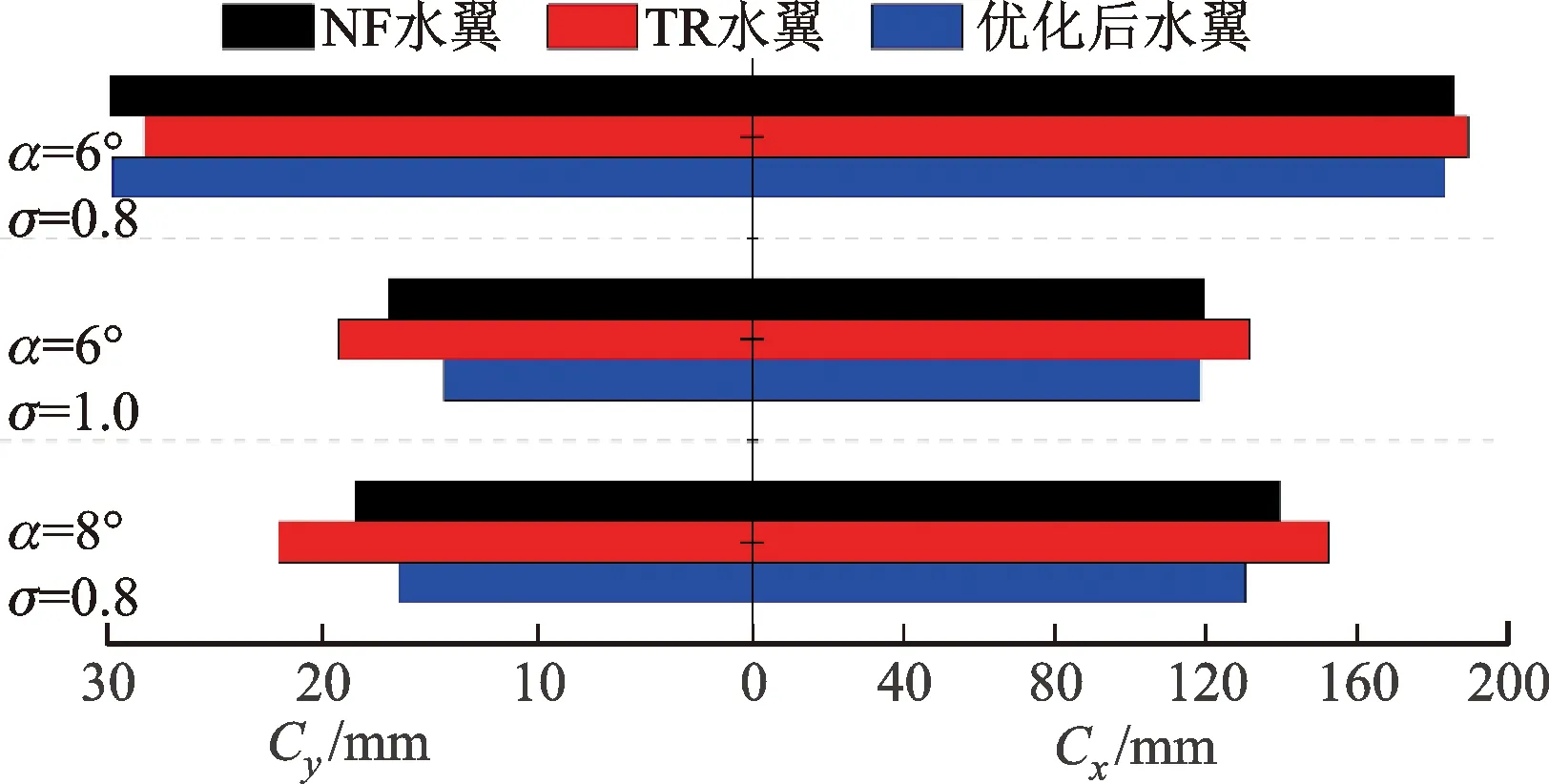
图16 优化前后水翼空化厚度和空化长度
图17和图18分别给出了攻角为6°、空化数为0.8条件下,控制结构优化前后,即TR6水翼和TR6-0.8水翼的气体体积分数与流线分布在一个周期内的变化,其中图17(a)和图18(a)为水翼周围流场图,图17(b)和图18(b)为控制结构附近局部放大图。优化后的TR6-0.8水翼对空化的抑制作用更大,空化的长度和厚度明显减小。与TR6水翼相比,TR6-0.8水翼的气体体积分数减小,空化流场得到改善。从流线分布可以看出,在空泡初生时刻,水翼尾缘处回射流还未产生,控制结构处由于自身形状原因产生涡结构。由于TR6-0.8水翼控制结构之间的间距大于TR6水翼,TR6-0.8水翼控制结构处的涡结构较大,因此TR6-0.8水翼控制结构对空化流场的改善作用更大。在空泡脱落时,由于回射流的切割作用,使空泡变的不稳定。从空泡脱落时控制结构处的流线分布可以看出,回射流受到3个连续控制结构的阻碍作用,向前缘的深入运动得到连续抑制。TR6水翼控制结构初始位置在弦长25%处,回射流绕过后面两个控制结构,虽然控制结构对回射流起到了阻碍作用,但是TR6水翼的控制结构位置离前缘较近,不仅没有起到抑制空化的作用,还导致空化长度和厚度增加。对于TR6-0.8水翼,由于控制结构的位置在弦长32%处,并且高度更大,回射流在绕过第二个控制结构到达第一个控制结构后,没有再绕过第一个控制结构,充分抑制了回射流向前的深入运动。同样的,优化后得到的TR6-1.0水翼和TR8-0.8水翼都对回射流产生了较大的抑制作用。通过布设连续流动控制结构,能够实现空化流场的局部调控,但需要合适的控制结构参数及布局,通过优化算法,快速实现了这一过程。
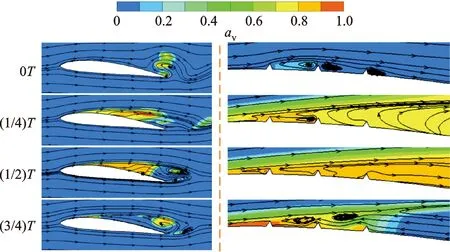
(a)水翼周围 (b)控制结构附近
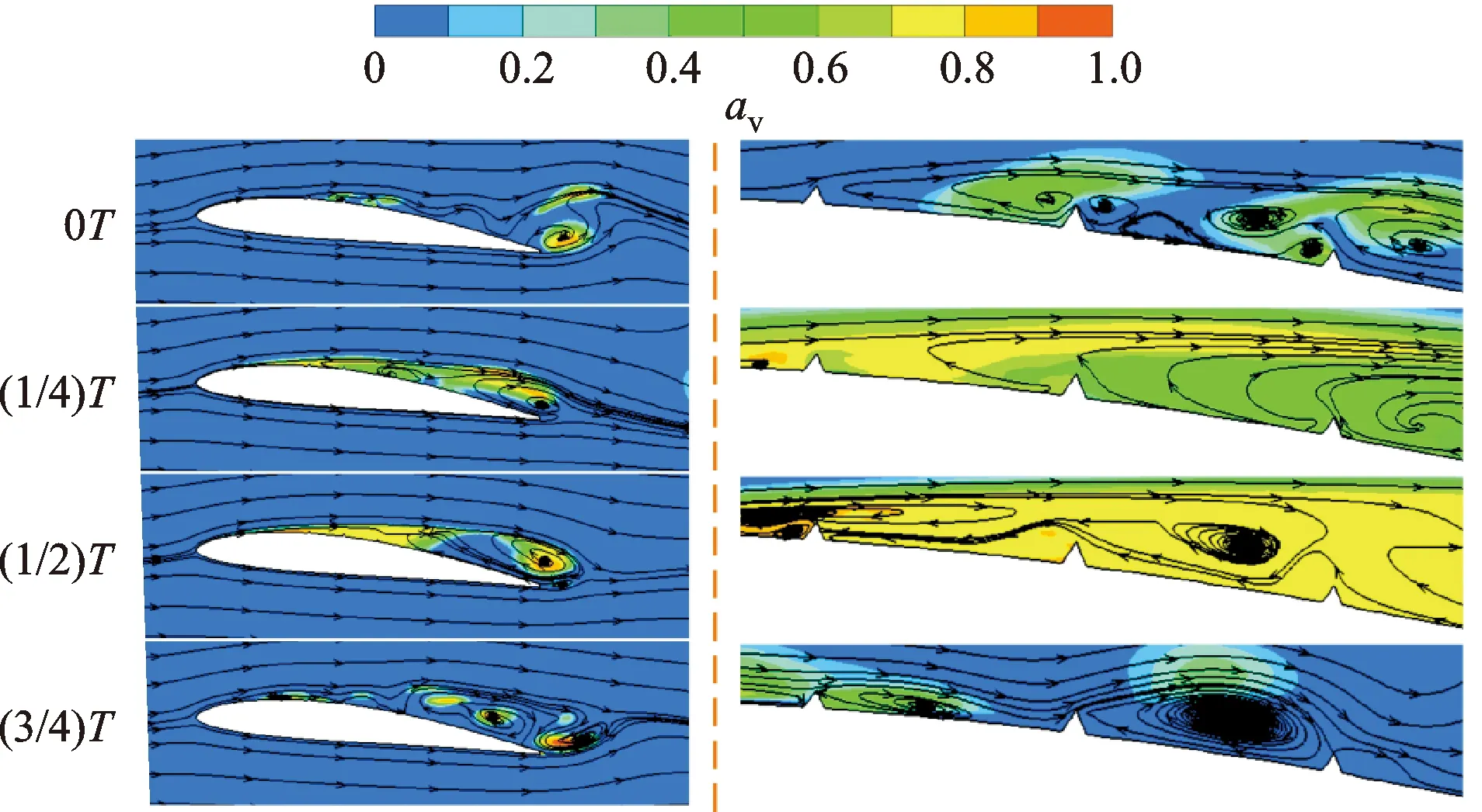
(a)水翼周围 (b)控制结构附近
4 结 论
本文在不同攻角和空化数的工况下,对NACA0009、NACA0012和Clark Y 3种水翼的流场进行了对比分析。通过改变型线,设计了新水翼,对空化流场进行整体控制。进一步地,结合广义模式搜索算法在新水翼吸力面布设多个控制结构进行了优化设计,对空化流场进行局部调控。主要研究结论如下。
(1)在相同工况下,3种水翼中Clark Y水翼的水动力性能最优,同一时刻不同水翼产生的空泡形态相似。对于同一水翼,空泡体积会随攻角的减小和空化数的增加而减小,相应的升阻比也会升高,水动力性能提升。
(2)为保持高升力系数的同时拥有较小阻力系数,新水翼型线的凸起高度需要介于Clark Y水翼和NACA0012水翼之间;在保持吸力面较大的凸起高度条件下,将最大凸起高度位置沿来流方向适当后移,可以抑制回射流的发展。
(3)新水翼的水动力性能优于NACA0009、NACA0012和Clark Y 3种水翼,升阻比明显提高,最大提高48.8%;与NACA0009和NACA0012水翼相比,新水翼抑制了回射流的发展,减小了空泡脱落频率,实现了对空化流场的整体调控。
(4)在新水翼吸力面布设连续控制结构,通过优化得到的TR6-0.8水翼升阻比进一步提高了9.5%,TR6-1.0水翼提高了13.6%,TR8-0.8水翼提高了4.8%,优化后水翼的水动力性能进一步提升,空化长度与厚度均有所减小,实现了对空化流场的局部调控。
(5)控制结构位置需要与水翼前缘具有一定的距离,如果控制结构离前缘较近,不仅不会起到抑制空化的作用,还会导致空化恶化。均匀布置的多个控制结构能够对回射流起到连续抑制作用,减小回射流对空化区域的影响。
