AUV 模块化对于操纵性的影响分析

刘隽，文永鹏，孙翔，朱心科，周焕银，尚红

(1.东华理工大学机械与电子工程学院，江西 南昌 330013；2.国电电力浙江舟山海上风电开发有限公司，浙江 舟山 316100；3.自然资源部第二海洋研究所，浙江 杭州 310012)

0 引言

不同的观测任务需要携带不同的传感器，而现有的AUV 设计对于更换传感器困难，因此模块化[1]是AUV 必然的发展趋势。设计能够携带多种传感器的舱段能够减少制造成本，可以根据观测任务的需要自由更换或增加舱段。

一般情况下，实现AUV 搭载更多探测设备的方法有增加附体、改变AUV 外壳外形和增加舱段等。在增加附体方面，赵金鑫[2]根据某些任务为AUV 设计了大尺度挂载，并根据操纵性分析对比，得出大尺度挂载对AUV 的操纵性运动的性能影响量，对于大型的附加载体采用该方法较好。在通过改变AUV 自身外形方面，许锦宇[3]设计出采取上下双半椭圆组合的橫截面结构，能让搭载的机械手收缩并贴合在AUV 的耐压舱外表面，并分析了AUV 在不同运动状态下机械手展开时与收起时受到力和力矩的变化，但在优化AUV 外形阻力时没有把舵和推进器加入考虑。在通过模块化设计方面，王鑫[4]根据模块化思想，设计出自定义舱段的机械结构，安装自定义舱段可以自行搭载更多传感或探测装置，同时对外形进行算法优化，有了兼具一定要求的容积和较小的直航阻力，但是在操纵性方面没有过多涉及。

考虑能源量、观测任务所需要的传感器体积尺寸以及制造成本等综合因素，本文研究的AUV 采用模块化设计，增加舱段搭载更多观测设备。良好的操纵性决定AUV 的稳定性、机动性，一定程度上影响着可携带能源量和使用成本，而增加舱段会对原来AUV 的操纵性产生影响，因此研究模块化AUV 的操纵性非常重要。

在借鉴上述研究结果的基础上，首先建立AUV 与加舱段AUV 的三维模型，通过Fluent 分别计算加装舱段的AUV 和未加装舱段AUV 的水动力系数，通过受力分析，建立数学模型进行仿真，给出水平回转运动仿真、水平面Z 形操舵仿真及空间定常螺旋下潜3 个方面的仿真结果，并分析加装舱段AUV 和未加装舱段AUV 操纵性发生的变化。

1 AUV 的模块化舱段设计

模块化设计的AUV 不同舱段之间采取螺纹连接方式，舱段可以设计为密封舱段或者透水舱段，这里设计采用透水舱段，舱段安装有传感器和浮力材料等，与密封舱段之间通过水密接插件进行数据传输与能源供给，在原AUV 上安装附加舱段后，会改变物理属性如质量、重心、排水体积等，并且也会改变计算的水动力系数数值，最终在操纵性上表现出来。

模块化AUV 与安装附加舱段的模块化AUV 设计参数如表1 所示。

表1 AUV 设计参数Tab.1 AUV design attributes

2 AUV 动力学分析与建模

建立坐标系，对AUV 的水动力、复原力、控制面作用力和推进器推理4 个方面的受力进行分析，建立完整的六自由度运动方程。

图1 模块化AUV 与附加舱段Fig.1 Modular AUV with additional compartments

2.1 坐标系的建立

建立空间运动坐标系描述AUV 的空间运动，如图2所示。采用国际水池会议（ITTC）推荐的和造船与轮机工程学会（SNAME）术语公报的体系分别建立惯性（定系）坐标系和动系坐标系。

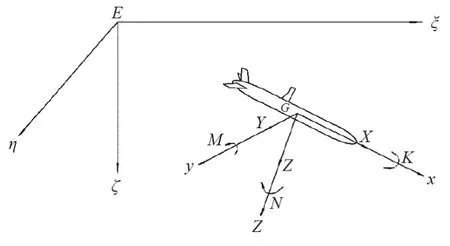
图2 惯性坐标系和动坐标系Fig.2 Inertial and moving coordinates

2.2 六自由度空间运动方程

由刚体动力学理论可得水下航行体在空间六自由度运动方程[5]的一般形式如下：

其中：

式中：m为AUV 质量；Ixx，Iyy，Izz分别为质量m对ox，oy与oz轴的转动惯量；XG，YG，ZG分别为AUV 重心坐标在随体坐标系的位置；u，v，w，p，q，r，分别为运动（加）速度，角（加）速度在动坐标系Gx，Gy，Gz轴的投影；X，Y，Z，K，M，N分别为作用力，力矩对动坐标系Gx，Gy，Gz轴的投影；Fluid，Propeller，Rudder 和Static 分别代表水动力（矩），推进器推力（矩），控制面舵力（矩）和复原力（矩）。

公式中的作用力与力矩X，Y，Z，K，M，N包括AUV 在航行过程中所受到的水动力（矩）重力（矩）和浮力（矩）、推进器的推力（矩）、控制舵的作用力（矩）。整个AUV 动力系统的控制输入分为对纵向的推进器推力Fu，水平舵的舵角 δs，垂直舵的舵角δr，AUV 系统为欠驱动系统。

2.3 水动力

AUV 所受到的水动力一般分为粘性水动力和惯性水动力两类。取等速直航状态（u0=V且u0≠0）作为泰勒级数展开点，将力和力矩泰勒展开并水动力只取到二阶项，考虑到AUV 几何模型的水平面非对称，得出下式[6]：

式中：Xqq，，等均为水动力系数；u，v，w，p，q，r，均为水动力函数的变量。

2.4 复原力（矩）

复原力（矩）描述艇身在横摇和纵摇自由度具备的横稳性和纵稳性，作用于AUV 上的静力包括重力B、浮力P及力矩M。由于重力和浮力的方向一般铅锤向下，所以在定系中的分量为（0，0，P-B）。在动坐标系表示[7]为：

重力P、浮力B对于随体坐标系原点的力矩为：

式中：（xB，yB，zB）为AUV 的浮心位置坐标；（xG，yG，zG）为AUV 的重心位置坐标；P为AUV 总重力；B为AUV 总浮力。

AUV 重心和浮心满足xG=xB，yG=yB，并且在中性浮力下重力P与浮力B相等，且相对于纵中平面对称。

2.5 控制面作用力

舵和桨布局方式为桨前舵，舵型为NACA0012 型。舵的外形参数[8]如表2 所示。

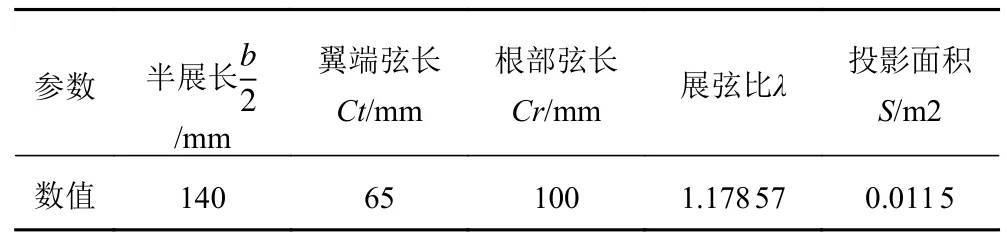
表2 NACA0012 外形参数Tab.2 NACA0012 Shape attribute

当攻角为α，速度为V时，舵受到力R的作用，可以分解为水平方向上的阻力D和与来流方向垂直的升力L，用升力系数CL和阻力系数CD来表征。本文研究的AUV 舵的升力系数与攻角关系、阻力系数与攻角关系如图3 所示。

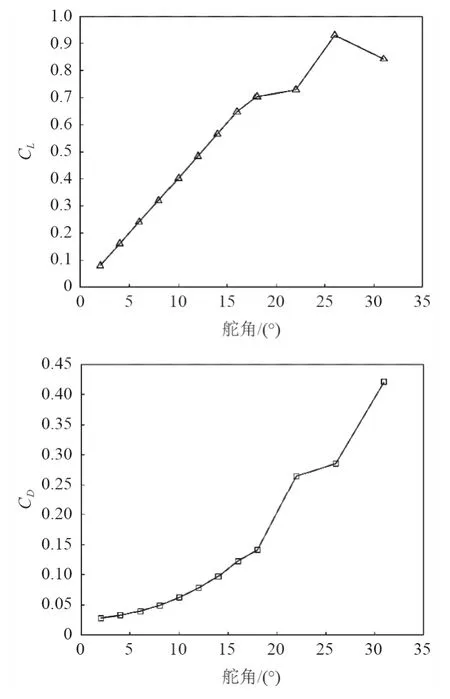
图3 NACA0012 舵的升力系数、阻力系数与攻角关系Fig.3 The relation between lift coefficient,drag coefficient and Angle of attack of NACA0012 rudder

使用Aitken 插值法最终得到的升力系数、阻力系数与舵角的函数关系式，并通过下式和舵翼安装位置得到对AUV 的力和力矩。

上式中：ρ 为流体密度；AR为舵翼投影面积；V为来流速度。

2.6 推进器推力

只在尾部安装有一个单螺旋桨作为推进器，通过试验和查询资料从而获取螺旋桨直径D、进速系数J、推力系数KT和转矩系数KQ，数据经过最小二乘法作最小二乘拟合处理，得到J与KT、J与KQ曲线，再通过AUV 航速V、当前螺旋桨转速n可求得推力T和扭矩Q。

螺旋桨主要参数如表3 所示。

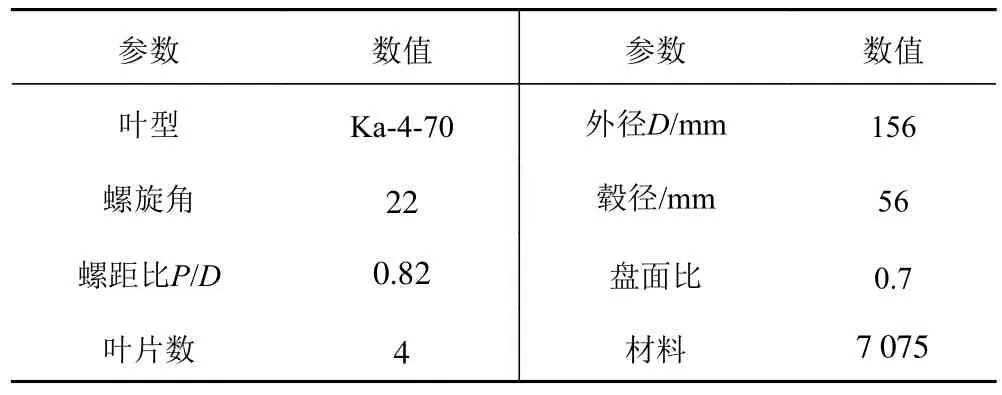
表3 Ka-4-70 螺旋桨主要参数Tab.3 Ka-4-70Main parameters of propeller

推力和转矩的表达式如下：

速度为0～2 m/s，令AUV 与加舱段AUV 以2 m/s直行，此时AUV 与加舱段AUV 的航行阻力分别为32.62 N 与37.38 N。螺旋桨推力系数KT与转矩系数KQ分别为KT=0.392 9，KQ=0.081 9，在725 r/min转速下，AUV 此时的螺旋桨推力与转矩为：

在765 r/min 的转速下，加舱段AUV 此时的螺旋桨推力与转矩为：

由上式可知，在不同转速下旋转的螺旋桨推力能够满足AUV 与加舱段AUV 在2 m/s 的直航阻力，该类型的螺旋桨能够满足要求。

3 AUV 水动力系数的仿真获取

计算AUV 六自由度运动方程所需要的水动力系数，通过分别划分AUV 和加舱段AUV 的重叠网格后导入Ansys Fluent[9]计算获得。模拟A U V 在∆u=0.25 m/s，u∈[0.25，2]直航试验[10]；水平面和垂直面斜航试验，其中漂角和攻角∆α，∆β=2°，α，β ∈[−14°，14°]；水平面和垂直面纯升沉和纯横荡试验、纯俯仰和纯摇首试验[11]，这4 种仿真通过设置Fluent 的UDF 文件进行[12]，其中震荡频率为0.2～0.625 Hz，纯升沉和纯横荡试验a=0.04 m/s，纯俯仰和纯摇艏θ0=0.1 rad。将得到的水动力系数进行无因次化处理[13]，仿真试验所得部分水动力系数如表4 所示。

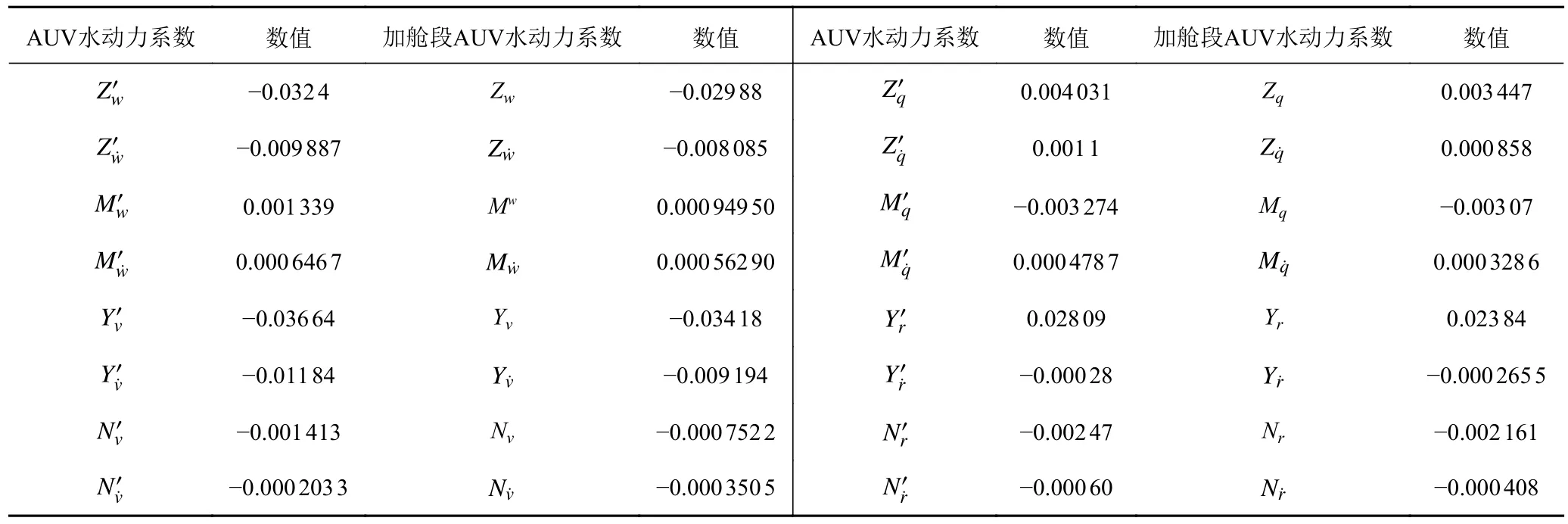
表4 PMM 仿真所得水动力系数Tab.4 hydrodynamic coefficients obtained by PMM simulation

水动力系数中含有大部分的耦合系数，为非线性系数，这些系数测定比较困难，博尔曼[14]于1989 年提出一种关于一些耦合水动力系数的近似关系式，由此可以推算出其他耦合系数。

4 建立AUV 六自由度运动仿真系统

通过Matlab 建立运动仿真程序，仿真流程如图4所示。首先初始化所有的运动状态变量，然后给输入变量赋值（推进器推力、垂直舵和方向舵的力矩），通过六自由度运动方程得到不同坐标系的加速度，根据四阶龙格库塔法[15]求解六自由度运动方程求出AUV 的状态变量（速度、位置和姿态），从而得到运动仿真的重心轨迹。

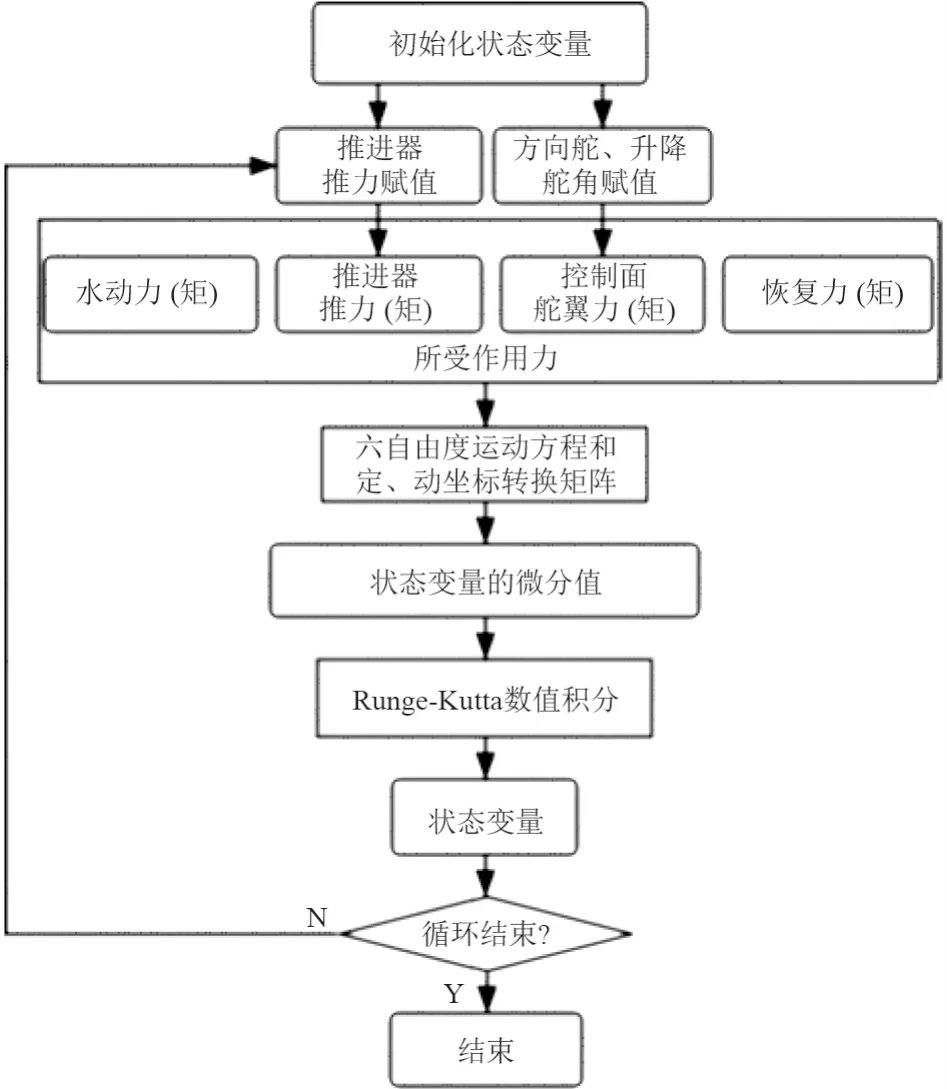
图4 AUV 运动仿真流程Fig.4 AUV motion simulation flow

5 AUV 操纵性分析

研究水平面回转运动、水平面Z 形操舵运动和空间定常螺旋下潜运动，并对AUV和加装舱段的AUV 的仿真数据进行对比，分析加装舱段后对原AUV 操纵性的影响和变化。

5.1 水平回转运动仿真试验

仿真试验为评价AUV 在水平面运动时的回转性能。设定直航速度为2 m/s，仿真总时长500 s，输入控制量的方向舵舵角δr=20°。重心在水平面的运动轨迹如图5 所示。

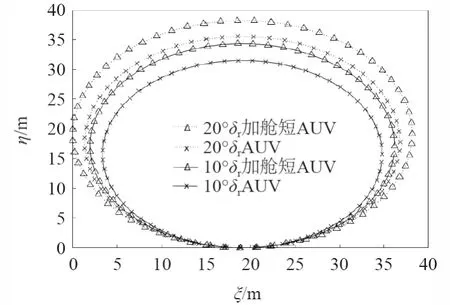
图5 10°与20°方向舵舵角下的AUV 与加舱段AUV 水平回转运动曲线对比Fig.5 Comparison of AUV and cabin added AUV horizontal rotation motion curves under different rudder angles

仿真结果如表5 所示。

表5 回转运动仿真结果Tab.5 Simulation results of rotary motion

定常回转直径D0指定常回转圆的直径。回转周期T0指在水平面回转运动中，从转舵起至回转360°所经历的时间。

5.2 水平面Z 形操舵仿真

该仿真试验是为了评价AUV 的航向改变性能。水平面Z 形操舵仿真时，设定直航速度为2 m/s，垂直方向舵舵角 δr/执行首向角 ψ为10°/10°，操舵速率为6°/s，仿真结果如图6 和表6 所示。

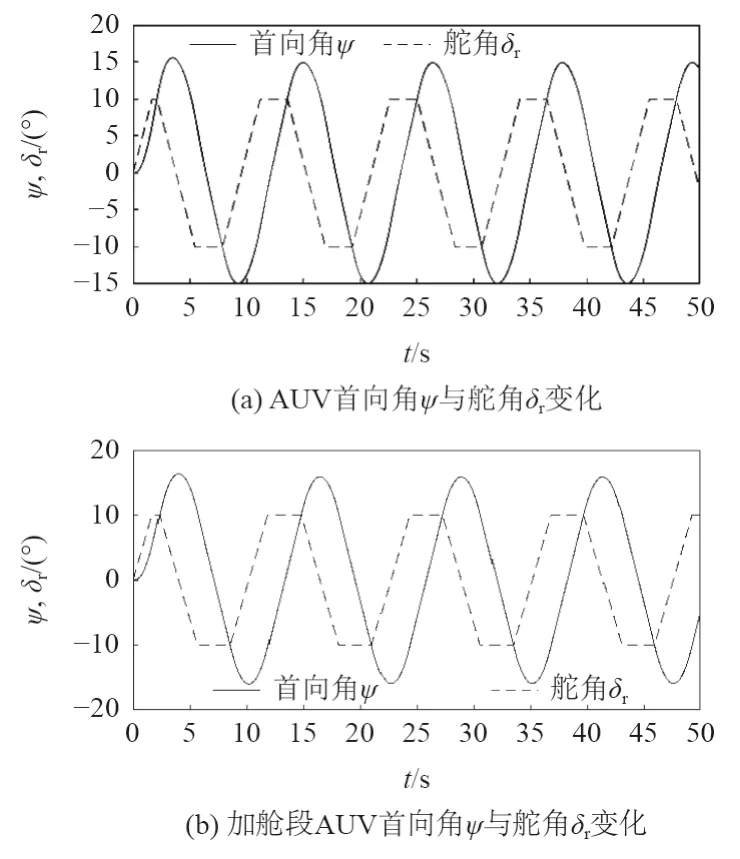
图6 水平面Z 形操舵仿真Fig.6 Simulation of horizontal Z steering

表6 水平面Z 形操舵仿真结果Tab.6 Simulation results of horizontal Z steering

初转期ta为首次操舵起至第一次操反舵止所经过的时间；超越时间tov指从操反舵开始到潜器停止朝原方向回转的时间；超越首向角 ψov指操反舵后潜器继续朝原方向回转所转过的最大角度；周期T指从操舵开始瞬间到潜器完成向右舷和左舷摆动各一次，回复到初始首向角的时间。

5.3 空间定常螺旋下潜运动仿真

该仿真试验是为了测定AUV 空间定常螺旋潜浮机动时的升矩和回转半径。仿真时使AUV 在适当深度以一个预定航速定深直航时，设定水平升降舵和垂直方向舵在预定舵角把定，此时AUV 就会同时进行回转和潜浮运动。空间定常螺旋运动的表征参数有水平面投影直径Ds和升距∆Ye。设定直航速度为2 m/s，输入控制量的方向舵舵角δr=20垂直升降舵舵角δs=20°，仿真时间为200 s，仿真结果如图7 和表7 所示。

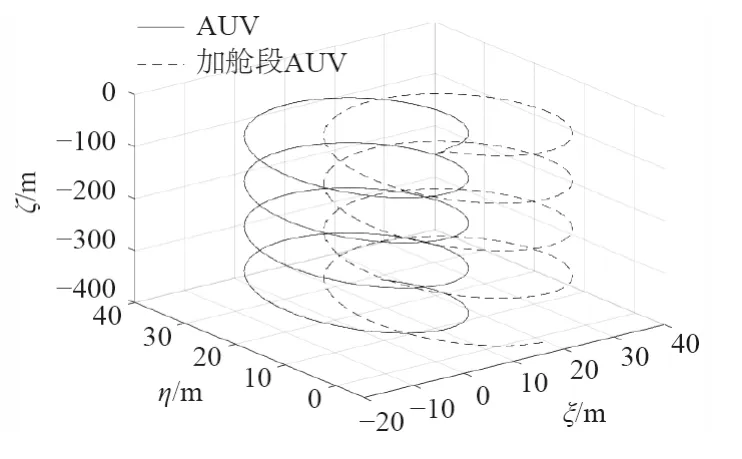
图7 u=2 m/s，δr，δs 为20°的AUV/加舱段AUV 重心轨迹Fig.7 u=2 m/s,δr,δs=20°AUV/ cabin added AUV center of gravity trajectory

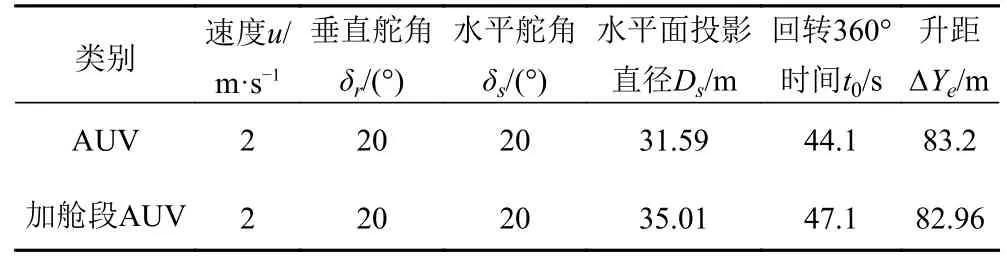
表7 空间定常螺旋下潜运动仿真结果Tab.7 Simulation results of space steady spiral diving motion

水平投影直径Ds指潜器的螺旋运动水平投影圆的直径。升矩指潜器回转360°潜深改变量。

5.4 操纵性分析对比

在水平面回转试验中，在设定条件下，加舱段AUV相比原AUV 的定常回转直径分别大了8.42%，11.37%，10.79%，12.83%，定常回转直径越大，表明加舱段AUV 相比原AUV 水平面内机动性降低。加舱段AUV 相比原AUV 的回转周期时间分别长了11.22%，9.07%，5.56% 和6.14%，表明加舱段AUV 相比原AUV 在大幅度转向的程度上减慢。因此在水平面回转实验中，加舱段AUV 与原AUV 相比，在同一舵角下回转直径D0要更大，回转周期T时间更长，水平面大舵角转向机动性更低。

在水平面Z 形操舵试验中，在设定条件下，加舱段AUV 相比AUV 初转期时间长了8.49%，加舱段AUV 相比原AUV 周期时间长了9.61%，表明加舱段AUV 相比AUV 首向改变减慢。加舱段AUV 相比AUV 的超越时间tov长了22.63%，加舱段AUV 相比原AUV 的超越艏向角大了14.83%，表明加舱段AUV 相比AUV 运动惯性增大。上述4 个特征量表明，加舱段AUV 相比AUV 对舵的响应较快，转首性较好、应舵较快。

在空间定常螺旋下潜试验中，在设定条件下，加舱段AUV 要比原AUV 的水平投影直径大10.83%，加舱段AUV 要比原AUV 的回转360°所需时间长6.8%，表明加舱段AUV 回转360°比原AUV 回转速度减慢。原AUV 要比加舱段AUV 的升矩大0.29%，表明加舱段AUV 比原AUV 下潜速度减慢。上述2 个特征量表明在三维空间的运动下，附加舱段的AUV 要相对于AUV 下潜减慢，空间运动性能下降。

6 结语

运用Solidworks 分别建立AUV 与安装附加舱段的AUV 的几何模型，并通过Ansys Fluent 分别计算AUV 与安装附加舱段AUV 水动力系数以及舵翼的水动力性能。建立AUV 操纵运动数学模型，通过进行AUV 与加舱段AUV 分别为水平回转运动、水平面Z 形操舵、空间定常螺旋运动操纵性仿真试验，对AUV 的操纵性能进行预报。最后对比AUV 与加舱段AUV 的操纵性试验所得试验数据，表明安装了附加舱段的AUV 相比原AUV的运动性、应舵性均下降。