间隙对水润滑轴承冷却性能影响研究
2023-06-15吴廉巍罗斌邹群
吴廉巍,罗斌,邹群
(1.海军装备部驻武汉地区第二军事代表室,湖北 武汉 430000;2.中国舰船研究设计中心,湖北 武汉 430000)
0 引言
水润滑轴润滑冷却是影响轴承摩擦、减振、磨损等性能的重要因素。敖庆章等[1]对水槽参数(角度、数量、深度)的作用进行了研究;戴燕[2]利用Fluent方法模拟了水槽参数、船尾倾角和轴承运行状态对轴承的冷却特性的变化;周春良等[3]采用流体力学方法,对船舶用水油密封的橡胶支座进行了计算,并对其内周向沟槽的作用进行了数值模拟;张国渊等[4]采用有限差分数值计算法,考虑了流体在流体中的紊流、粘度、密度、压强和压强的关系[5],采用雷诺方程,计算了流体在流体中的三维压力场[6]和温度场的分布和动态特征。在使用水润滑的情况下,通常要将轴套安装在轴颈上,以避免水对其进行腐蚀。为了保证后轴和内衬之间的牢固连接[7],不会出现相对松动和打滑,必须使用干涉的方式[8]。关于过盈配合的过盈量,在技术上没有具体规定,也没有具体的计算,通常由设计人员根据实际情况来确定。
杨成仁等[8]在水润滑的基础上,进行了大量的理论分析和实验比较。研究发现,轴承间隙、载荷和速度对影响动压水膜成形的主要影响因子是:相同的材质和表面质量,在相同的速度下,随着轴承的缝隙增加,载荷容量降低,而随着间隙的减少,载荷容量增加。与普通的多通道式水油橡胶轴承相比,在60~70 mm 轴颈处,其最大的间隙是0.12~0.14 mm。这些结果可为确定水力润滑轴承的缝隙提供参考。
段芳莉[9]在MARC 的基础上,建立了适用于各种流体状态下的雷诺方程,研究了平面和凹面式的油膜润滑特性,对其在不同工况下的偏位角、膜厚形状、压力分布、承载能力及摩擦因数进行了数值模拟,并对平面和凹面式橡胶层在静接触状态下的变形及应力变化情况进行了分析。余江波[10]应用多层格子方法,对一、二维介质中污水润滑的橡胶轴承进行了计算。采用Herrebrugh 最小厚度公式对于结构特殊的水润滑轴承进行了仿真计算,得出了在这种尺寸下,水润滑轴承的润滑状况随着速度和负载改变而发生的规律。
结果表明,由于在轴承内部有间隙,间隙处的水流状况发生变化,势必会对压力分布、速度分布、橡胶衬层及承载量等造成一定的影响。在各种工作条件下,水润滑轴承的润滑状态可以分为混合润滑、部分弹性流体动压润滑和完全弹性流体动压润滑。
在实际应用中,由于设备的启停以及外部负荷的急剧改变,使得轴颈和支座发生了碰撞和摩擦[11],并产生了较多的热。试验转轴的高转速运行,也会对水膜做功,从而提高水膜的温度。高温会对其工作特性产生一定的不利作用[17],所以必须将其迅速地进行散热。但由于密封垫的间隙太窄,无法充分发挥出良好的散热作用,因此,为了提高其散热性能[18–20],必须在其内部加大轴承直径。在橡胶轴承中,存在的空隙不仅可以改善其热辐射[21],而且可以改善其耐摩擦材料的磨蚀特性。
本文就转轴和轴承内衬过盈配合的过盈量作为可变条件,轴承水膜的温度分布及温度最高值作为输出结果,分析结果并讨论。
1 冷却分析理论体系
1.1 温度计算过程
轴承的热源主要有内部和外部热源两部分,前者如摩擦热,后者如冷却水初始温度等。
与之相比,轴承的热源以摩擦为主。摩擦热值与摩擦力矩和轴承转速有密切关系。由该方程推导出的摩擦力矩为:
式中:P为作用在轴承上的载荷;d为轴颈直径;μ为轴承的摩擦系数。
轴承摩擦热计算公式为:
式中:n为轴的旋转速度,r·min−1。
轴承热流密度计算公式为:
式中:l为轴承长度,m。
以式(1)~式(3)计算船舶轴系尾轴承的摩擦热流量。
1.2 流体流动状态
水润滑轴承内的流动状态,按照雷诺数Re判断。
式中:ρ流体密度,kg/m2;u为平均流速,m/s;d为管道直径,m;μ为动力粘性系数,N(m2·s)。
1.3 冷却水流量
尾轴架轴承利用海水进行润滑和冷却的,其入口流量跟航速以及导流罩的工作状态有关。尾轴架轴承上有n个水槽,每个水槽面积为s1mm2,水膜横截面积为s2mm2,过流面积为S:
冷却水流量为Q1时,与v1对应的尾轴架轴承入口流量是冷却水流量和过流面积的比值,公式为:
2 冷却有限元分析过程
2.1 水润滑轴承内径参数
如图1 所示,不同内径的轴承对应有不同的间隙值,随着轴承内径的增加,间隙值也在不断增加,呈现正相关关系。
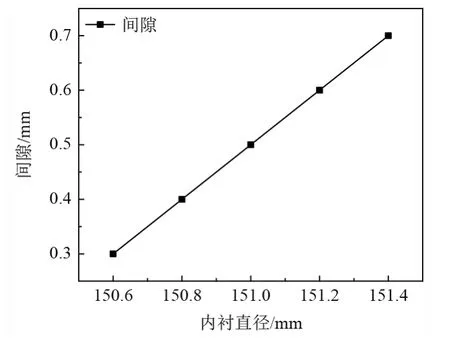
图1 轴承内径与间隙值的变化曲线Fig.1 Variation curve of bearing bore and clearance value
表1 为6 种轴承的内径参数及间隙值。
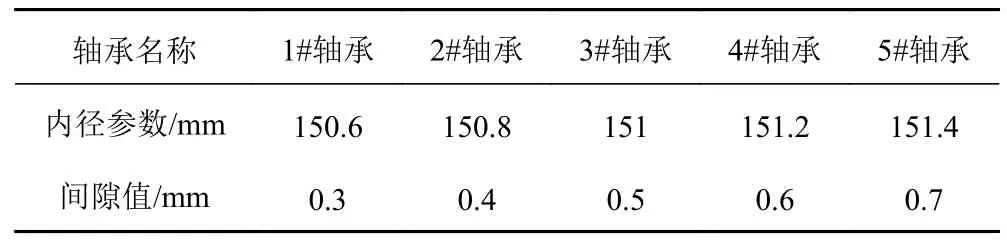
表1 不同轴承内径及间隙值Tab.1 Different bearing bore and clearance values
图2 为不同轴承的最小水膜厚度和最大水膜压力,表2 为润滑计算结果。
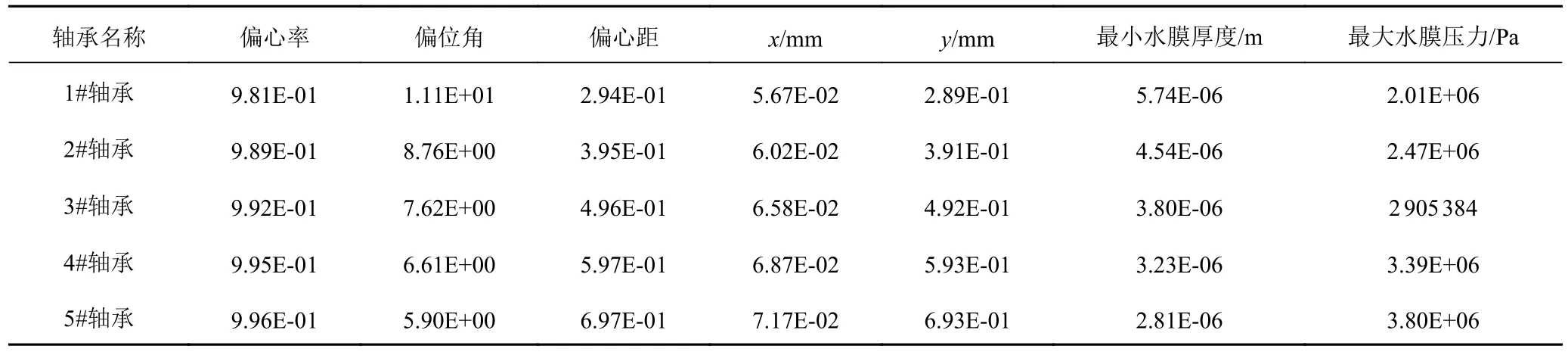
表2 润滑计算结果Tab.2 Lubrication calculation results
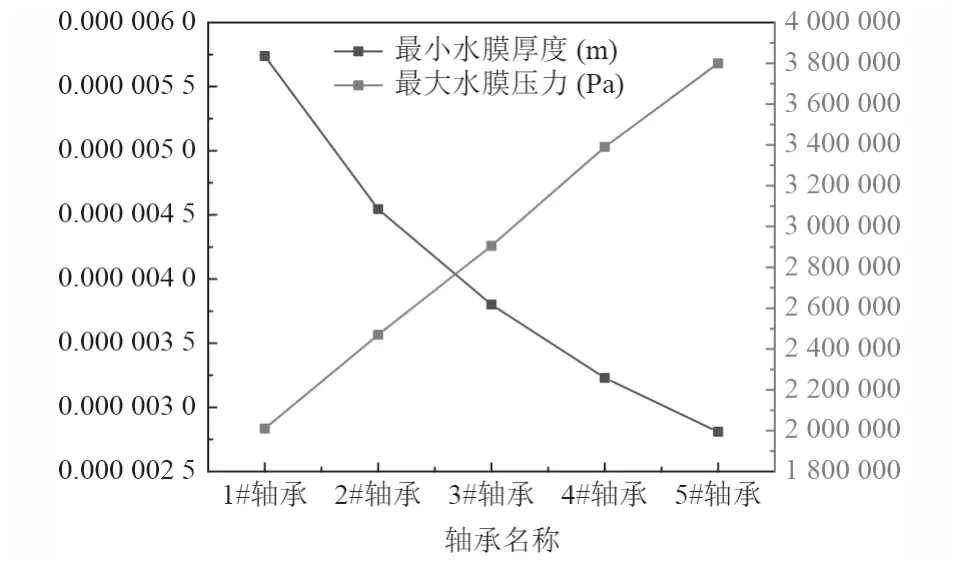
图2 不同轴承的最小水膜厚度和最大水膜压力Fig.2 Minimum water film thickness for different bearings,maximum water film pressure
分析数据表明,随着轴承内径的增加,偏心率、偏位角、偏心距有所增加;同时水膜的旋转中心也在不断向着第1 象限的正方向偏移;偏心度增大,水膜压力和承载能力增大;随着轴承内径的增加,最大水膜压力不断增加,而最小水膜厚度不断减小。
本文得到的最大水膜压力、最小膜层厚度等数值与已有的文献[9]进行了比较。通过与试验数据的比较,表明本文所建的模拟方法是可行的,模拟的效果可以很好地反应出水润滑轴承润滑的特点。研究表明轴承间隙是影响水膜压力、水膜分布和承载能力的重要因素。
2.2 有限元建模
1)建立水膜模型
利用SolidWorks 软件建立多沟槽水润滑轴承的水膜模型,如图3 所示。

图3 仿真水膜模型Fig.3 Simulated water film model
2)流体域网格划分
网格的分割直接关系到数值解的准确性、求解速度和收敛速度。
多沟槽水润滑轴承具有多个弧形、多个凹槽,而且流体的厚度方向比轴向和圆周向的直径都要小得多,常规的六面体网格划分方法很困难,需要用 ICEM专用的流体网格软件。ICEM 是应用于流体力学建模的前处理软件,在ICEM 的基础上进行网格分割,如图4 所示。
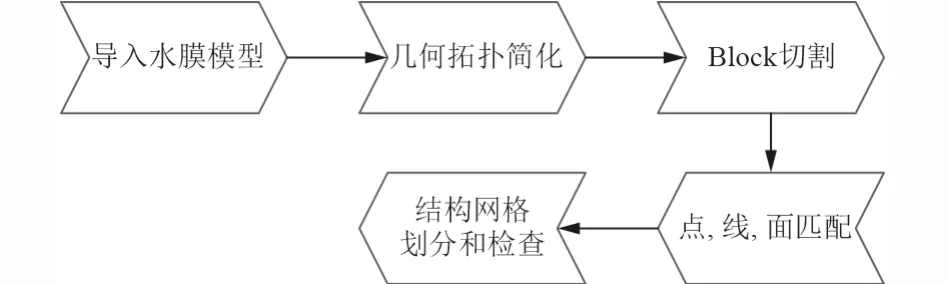
图4 网格划分流程图Fig.4 Flow chart of grid division
利用 ICEM CFD 模块进行单元分割,可以实现对整个单元进行整体的控制,实现对单元数目的有效控制,以获得高品质的网格。另外,在膜厚度的Y向上设置3 个格子,以更好地模拟流场厚度的流动和动态。其他部件则需要更少的栅格,每个单位的大小只有2 mm。该系统具有114257 个单元,可以对其进行简单的单元分割。设置固态节点的数目为13130,如图5 所示。

图5 水膜网格Fig.5 Water film grid
图6 轴承水膜模型边界条件设置Fig.6 Bearing water film model boundary conditions settings
3)模型材料的确定
该轴承包括2 个部件:1 个是铜套,1 个是高分子材料,轴承的材质见表3,主轴是用海军黄铜制作。
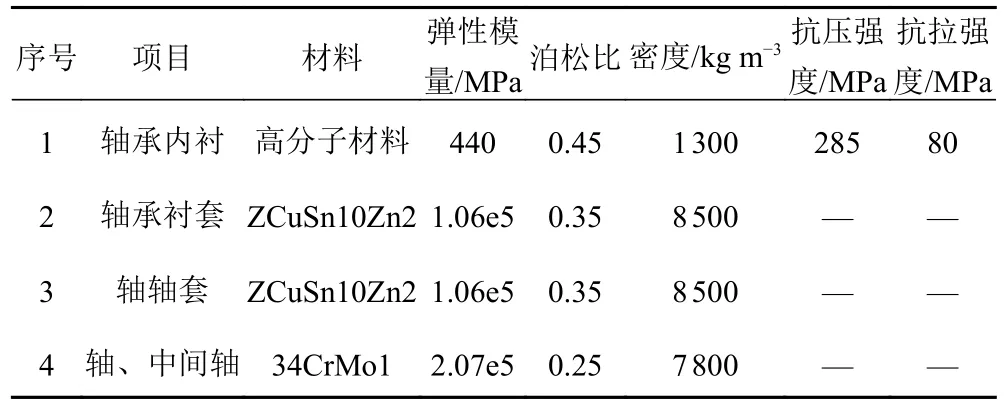
表3 水润滑轴承与试验转轴材料Tab.3 Water-lubricated bearings and test spindle materials
4)边界条件设计
求解区边界主要包括入口边界、压力出口边界、外壁面边界和旋转墙边界4 个部分,水膜内壁作为热流量的热源。
5)冷却水流量
艉轴架轴承利用海水进行润滑和冷却,其入口流量与航速及导流罩的工作状态有关,一般根据经验进行设定。
6)水槽过流面积
尾轴架轴承上有7 个水槽,每个水槽面积为800 mm2,水膜横截面积为smm2,过流面积为S。
轴承内径与过流面积的关系如表4 所示。
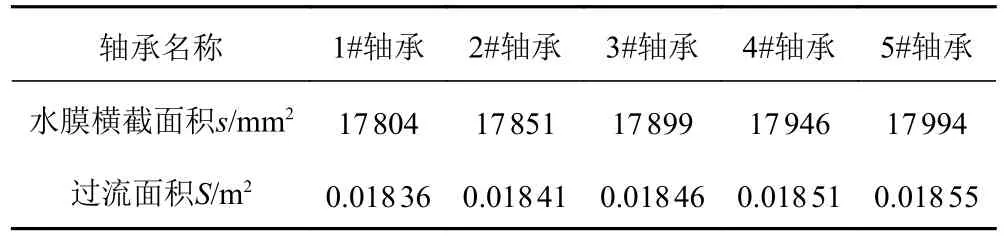
表4 轴承内径与过流面积的关系Tab.4 Relationship between bearing inner diameterand overflow area
7)入口流量
冷却水流量为Q=13 m3/h时,与vi对应的轴承入口流量如表5 所示。

表5 不同试验轴承的入口流量计算Tab.5 Calculation of inlet flow rate for different test bearings
具体边界条件设置如下:
1)入口边界是冷却水进口。通过经验公式,采用不同的进口流速vi,0.08 MPa 的进口压力。
2)出口边界是具有0.075 MPa 的压力出口。
3)将模型的外围设置为壁面边界,而将外壁材料作为轴承内衬,并假设不存在任何物质置换,具有粘滞特性的非滑动状态。
4)由于试验转轴围绕轴的中心转动,试验转轴的内壁被设置为旋转墙,并且转动墙的材料被设定为轴套管的外壁表面,旋转速度为200 r/min。该模型的传热极限是恒定的热通量。在此基础上,对某一转速下滚动轴承的摩擦热进行求解,并将其平均分配到水膜的内壁上,也就是在模型旋转壁的边缘状态下,其入口处的初始温度为305 K(32°C),而除了旋转的墙壁之外,其他的壁面都是等温的,在305 K 左右。
3 冷却结果分析
划分网格阶段完成,导入Fluent 软件进行后处理,进水口温度统一设置为32°C,入口流速为vi,5 个轴承水膜的温度云图如图7 所示,最高温度值及温度上升幅度如图8 所示。

图7 不同轴承内径最高温度变化的冷却结果Fig.7 Cooling results for different bearing inner diameter maximum temperature variation
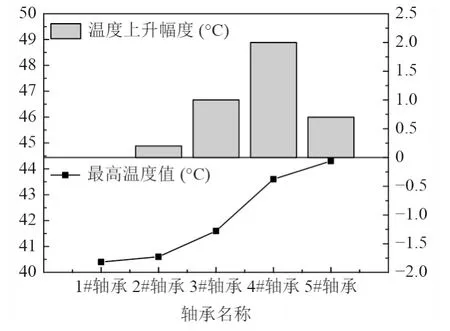
图8 不同轴承最高温度变化及温度上升幅度Fig.8 Variation of maximum temperature and temperature rise of different bearings
结果表明,温度上升幅度n是由上一个最高温度值ki减去下一个最高温度值ki+1的结果除以上一个最高温度值ki的百分比。温度上升幅度可以反映不同间隙的轴承对于温度的敏感性。随着轴承间隙越大,最小水膜厚度反而越小。这是由于进水流量一定,整体的间隙变大后,水膜分布范围变大,从而导致最小水膜厚度遭到稀释,最终导致了间隙由0.3 逐步增加到0.7,最高水膜温度由40.4°C 上升到44.3°C,并且随着间隙越来越大,在间隙0.3~0.6 mm 阶段,温度增幅逐步提高,在间隙0.6~0.7 mm 阶段增幅减小,说明在间隙0.6 mm 是水膜最高温度的突增点。
4 结语
1)对于铜套配合来说,过盈量是最大的敏感因素。同样结构的水润滑轴承,轴承间隙越大,轴承的最小水膜厚度越小,最大水膜压力越大。本文建立的轴承间隙从0.3 mm 逐步升高至0.7 mm,最小水膜厚度5.74E-03 mm 降低至2.81E-03 mm,间隙0.3 mm 时的最大水膜压力是2.01E+06 Pa,增加到间隙0.7 mm 时的最大水膜压力为3.80E+06 Pa。
2)随着轴承间隙的逐步提高,轴承水膜最高温度持续增加,在轴承间隙0.3 mm 时计算出的最高温度为40.4 °C,在轴承间隙0.7 mm 时计算出的最高温度为44.3 °C。其中温度增幅在间隙0.3~0.6 mm 时持续增加,在间隙0.6~0.7 mm 时降低,说明轴承间隙对于最高温度有一个温升突变点为,间隙0.6 mm 时刻。设计水润滑轴承时应充分考虑轴承间隙的因素,避开轴承温升的突增点。
