综合环境因素影响下预应力混凝土安全壳变形规律研究*

汪 全 赵东拂,2,3,4 杨昕光

(1.北京建筑大学土木与交通工程学院,北京 100044;2.北京建筑大学大型多功能振动台阵实验室,北京 100044;3.北京建筑大学工程结构与新材料北京市高等学校工程研究中心,北京 100044;4.北京建筑大学北京节能减排与城乡可持续发展省部共建协同创新中心,北京 100044;5.中冶建筑研究总院有限公司,北京 100088)

核电厂发生核事故时,安全壳作为阻止裂变产物向环境泄漏的最后一道屏障,确保其完整性尤为重要[1]。为了验证安全壳的整体密封性、结构性能和强度是否满足要求,在机组首次换料大修及后续每十年必须进行安全壳结构整体性试验。

在该试验中,预应力混凝土安全壳结构主要承受试验压力作用,并对其变形、应变、温度、预应力钢束力值等进行监测,是一种典型的低荷载、小量程的精密试验,测量精度要求较高[2]。例如,在最大试验内压作用下,穹顶竖向位移仅为安全壳高度的万分之一左右,而变形测量精度需达几十万分之一。因此,需考虑诸如环境温度、太阳辐射、风速等综合环境因素对安全壳结构整体性试验的影响,对安全壳变形进行合理的修正,以得到符合精度要求的测量结果。

目前,国内外关于环境因素作用下结构温度场及作用效应的研究主要集中在桥梁、水工结构等工程领域[3-5],对于安全壳结构的相关研究尚不够深入。林志伸等通过理论推导和编程计算,分析了外围环境因素作用下安全壳的温度场,计算结果与实测结果吻合较好[6]。刘世豪通过有限元方法分析了施工初期安全壳的温度场及温度应力,更准确地预测了安全壳整体和局部开裂情况[7]。黎鹏飞等采用大型有限元软件对安全壳分别进行了正常运行、严重事故工况下的稳态和瞬态分析,模拟了安全壳的温度场变化,确定了最不利温度效应[8]。张冰基于热传导和热对流模拟计算了安全壳在整体密封试验时内部温度场分布情况,验证了安全壳34 m以上空间温度出现分层分布现象[9]。

综上,为提高安全壳整体性试验的变形测量精度,并对其进行合理的修正,研究环境温度、太阳辐射等综合环境因素作用下预应力混凝土安全壳的变形规律是十分必要的。通过有限元模拟,研究环境温度、太阳辐射、辐射换热以及不同热边界条件施加方法对安全壳变形的影响规律,探明预应力混凝土安全壳结构在综合环境因素下的变形规律,研究可为安全壳结构整体性试验与核电厂安全运行提供理论与技术支持。

1 理论方法

1.1 热传导方程

基于傅里叶热传导理论[10],忽略混凝土内部产生的热量,可得热传导方程如下：

(1)

式中：λ为混凝土的导热系数,W·m-1·K-1;T为结构表面温度;n为表面法线方向;I、Qc、Qr分别为太阳总辐射、对流换热和辐射换热的热流密度,W·m-2。

1.2 热边界条件

环境因素作用下安全壳的热边界可分为三类：太阳辐射、对流换热和辐射换热。太阳辐射包括太阳直射辐射、散射辐射以及太阳辐射到达地面后的反射辐射。对流换热为安全壳与内外空气的热交换。辐射换热包括结构向环境发射的辐射和环境向结构发射的辐射。

上述三类热边界施加主要有两种方法：1)分别施加法[11],即将太阳辐射、对流换热和辐射换热边界条件通过不同的方式同时施加于结构上;2)综合系数法[12],即将太阳辐射、对流换热和辐射换热转化为综合温度和综合换热系数进行施加。

1.2.1热边界分别施加

安全壳热边界条件复杂,为了简化计算,将上述不同热边界条件使用Robin边界进行求解[13]：

(2)

式中：α为混凝土太阳辐射吸收系数;I为太阳总辐射强度,W·m-2;hc、hr分别为对流换热系数和辐射换热系数,W·m-2·K-1;Ta、T分别为环境温度和结构表面温度,℃。

对流换热系数与结构表面粗糙度、风向、风速等有关,其中风速影响最大,聂玉东对众多对流换热系数进行回归分析[14],并按式(3)计算对流换热系数：

hc=4v+5.4

(3)

式中：v为风速,m/s。

辐射换热主要与辐射发射者和辐射接受者的温度以及物体有关,辐射换热系数可由式(4)计算[15]：

hr=εC0(546+Ta+T)[(273+Ta)2+(273+T)2]

(4)

式中：ε为物体辐射发射率,混凝土结构取值为0.88,空气取值为0.82;C0为斯蒂芬-玻尔兹曼常数,其值为5.67×10-8W·m-2·K-4。

1.2.2综合换热系数和综合温度

将式(2)化简成下式：

(5)

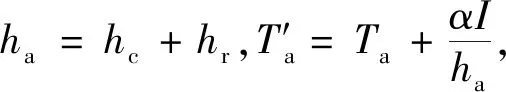
(6)

式中：ha为综合换热系数;T′a为综合温度,式(6)表示环境温度叠加太阳辐射、对流换热和辐射换热的一个综合效果。

1.3 太阳辐射强度

安全壳接收到的太阳辐射主要有三部分：太阳直射辐射、太阳散射辐射、太阳直射辐射和散射辐射到达地面后的反射辐射。

1.3.1太阳直射辐射强度

太阳辐射穿越大气层时,不改变原来传播方向的为太阳辐射直射强度[16]。一般认为太阳直射辐射强度在穿越大气层时按指数规律衰减,Kehlbeck基于Bouguer-Lambert定律提出一种幂指数模型用于计算光线垂直的平面太阳直射辐射强度[17],即：

Id=I0Pm

(7)

其中P=0.9tu·ta

m=1/sinh

式中：I0为太阳常数,取1 353 W·m-2;P为大气透明系数[18];tu为林可氏浑浊度系数;ta为相对压强;m为大气质量;h为太阳高度角。

1.3.2太阳散射辐射强度

太阳辐射穿越大气层时被大气层散射部分中的一部分从各个方向散射到结构表面的为太阳散射辐射强度[16]。太阳散射辐射强度通常与结构表面的方位角无关与表面倾角有关,水平面散射强度可按下式计算[19]：

Is=(0.271I0-0.942Id)sinh

(8)

其他倾斜面散射强度：

(9)

式中：θ为表面倾角,即斜面与水平面之间的夹角,筒身θ=90°。

1.3.3地面反射辐射强度

太阳直射辐射和散射辐射到达地面后,一部分被地面吸收,一部分被地面反射回去,反射回去的为地面反射辐射强度[20]。反射辐射强度可按下式计算：

(10)

式中：r为地面太阳辐射反射系数,取0.2。

综上所述,结构物接收到的太阳总辐射强度可按下式计算：

I=Idcosφ+Is+Ir

(11)

式中：φ为太阳入射角,穹顶可认为cosφ=sinh。

刘诚通过太阳辐射模型计算得到北京地区晴天水平地面的太阳辐射强度与实测值吻合良好[11],说明了该模型的适用性和正确性。

2 工程概况

某核电站安全壳结构形式为带密封钢衬里的预应力混凝土结构,外形为带圆穹顶的圆柱形筒体,剖面见图1。该安全壳具有4个扶壁柱,沿筒均匀分布,且设备闸门孔竖向中线与206.666 gr(gr为角度单位,1 gr=0.9°)扶壁柱中线重合,筒体内径37 m,壁厚0.9 m。穹顶内半径为24 m,壁厚0.8 m,扁球壳。钢衬里厚6 mm,底板厚5.5 m。安全壳混凝土强度等级PS40。由廊道顶部至筒体顶部布置144根竖向预应力钢束导管;环向布置223根钢束导管,每根钢束呈360°包角,均匀锚固在4个扶壁柱上。穹顶设置174根钢束导管,钢束锚固于环梁。钢绞线穿入钢管,张拉后注入水泥浆,避免钢绞线的腐蚀。

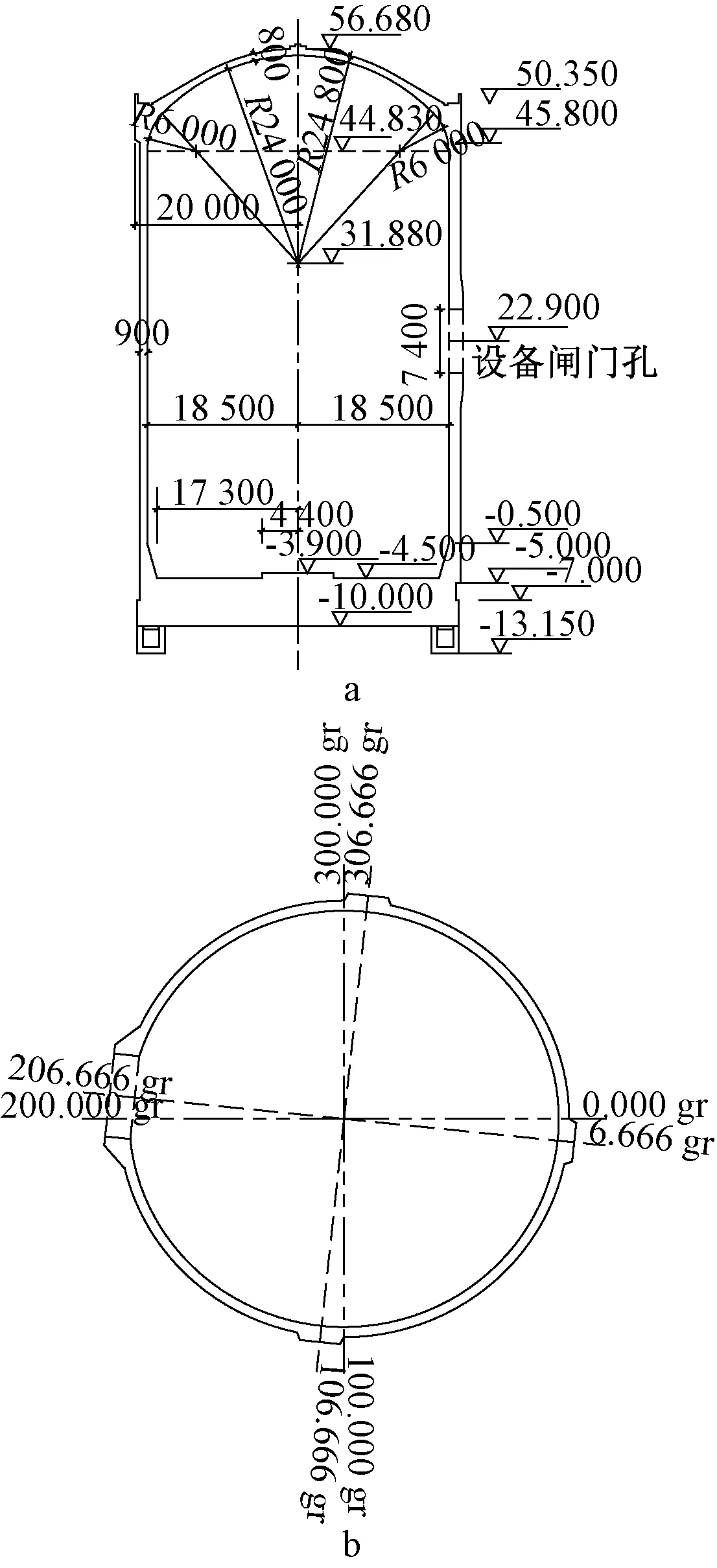
a—安全壳结构竖向剖面(高程单位为m,其他单位为mm);b—安全壳结构水平剖面(+22.9 m)。图1 安全壳结构剖面Fig.1 Structural cross-section of containment

3 有限元模型与参数

3.1 有限元模型

采用大型通用有限元软件ABAQUS进行计算分析,预应力混凝土安全壳有限元模型如图2所示。考虑到计算精度和计算成本,筒身和穹顶选用温度位移耦合的C3D8T和C3D6T三维实体单元。预应力钢束选用温度位移耦合的T3D2T杆单元,预应力钢束采用Embedded约束到混凝土中。钢内衬选用温度位移耦合的S4T和S3T壳单元进行模拟。钢内衬与混凝土采用Tie绑定约束。

a—混凝土壳体;b—钢内衬;c—预应力钢束。图2 预应力混凝土安全壳有限元模型Fig.2 Finite element model of pre-stressed concrete containment

3.2 边界条件

在ABAQUS中可将太阳辐射定义为荷载,通过Thermal中的surface heat flux进行定义,属于第二类热边界条件。对流换热可在ABAQUS Interaction模块,通过surface film condition定义,属于第三类热边界条件。辐射换热根据式(2)近似通过第三类热边界条件在Interaction模块中surface film condition定义。如采用综合换热系数和综合温度,将三种热边界转化成对流换热边界,可在ABAQUS Interaction模块,通过surface film condition进行定义,综合换热系数即film coefficient,综合温度即sink temperature。

3.3 材料参数

混凝土太阳辐射吸收系数α为0.6[21]。其他材料参数见表1。

表1 材料参数Table 1 Materials parameters

3.4 环境温度

计算模拟时间选用5月下旬某连续6日,起算时间为上午10时,计算总时长为144 h,天气晴,气温18～30 ℃,风力3级。安全壳结构初始温度为24 ℃。

假设白天环境温度按余弦变化,夜间环境温度按线性变化,环境温度可按下式计算[11]：

Ta(t)=

(12)

式中：Tmin和Tmax分别为日最低和最高气温,分别为18 ℃和30 ℃;tr和ts分别为日出和日落时间,以小时为单位,按24 h制计算,分别为6时和18时;td和tn分别为白天和夜间时长,td=ts-tr,tn=24-td。假设安全壳壳内空气温度保持恒定为24 ℃。

3.5 换热系数

假设计算周期内风力为3级,故安全壳外表面风速取4 m/s,由式(3)计算得到外表面对流换热系数为21.4 W·m-2·K-1。安全壳内部风速为0,内部对流换热系数为5.4 W·m-2·K-1。

由式(4)可知辐射换热系数是一个关于结构温度和环境温度的函数。文献[14]表明,当辐射换热系数取一个固定近似值时对计算结果影响较小,满足精度要求。因此取辐射换热系数近似值为5.4 W·m-2·K-1。

4 计算工况

计算分析了4种工况下预应力混凝土安全壳的变形响应。工况1：将太阳辐射、对流换热和辐射换热三种热边界以不同施加方式同时施加在结构表面。工况2：将三类热边界转化成综合换热系数和综合温度施加在结构表面。工况3：忽略太阳辐射,其他设置同工况1。工况4：忽略辐射换热,其他设置同工况1。本文根据实际情况作了如下简化与假设：1)穹顶不考虑太阳辐射到达地面后的反射辐射;2)筒身由于受到周围核电厂房的遮挡,假设筒身不受太阳直射辐射影响。具体工况见表2。

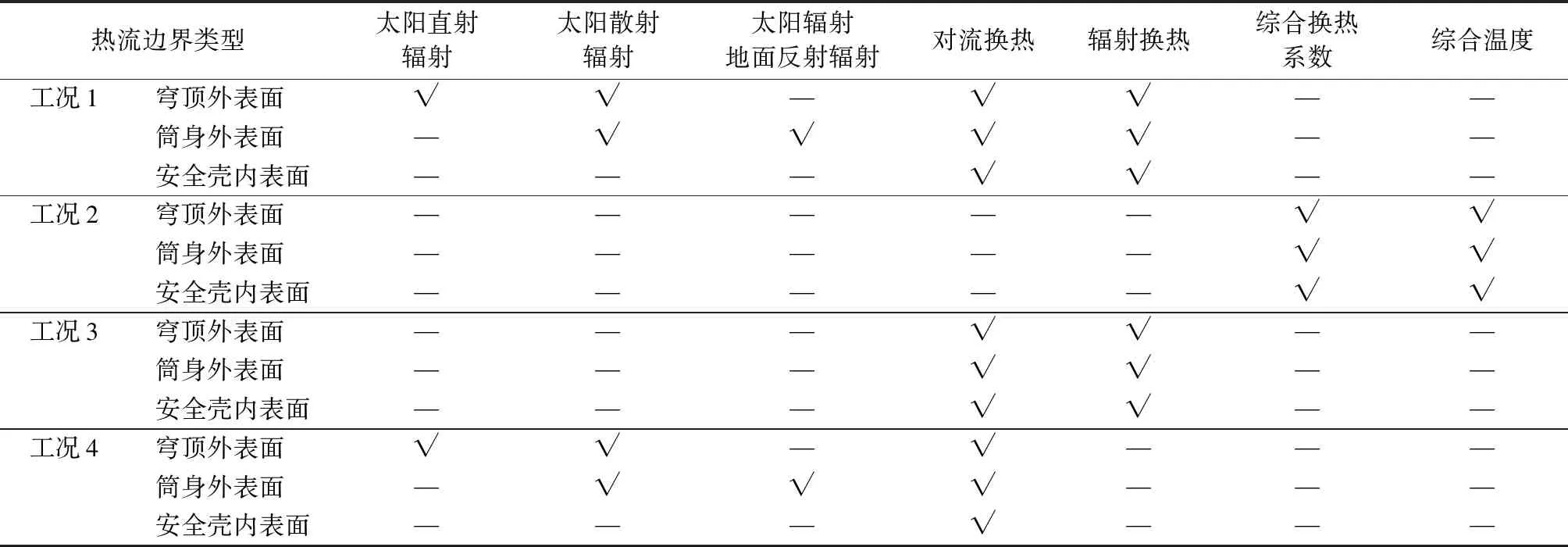
表2 安全壳热流边界详情Table 2 Details of containment heat flow boundary

5 结果分析

通过ABAQUS进行了4种工况的模拟计算,各工况的安全壳位移等值线云图如图3～6所示。在4种工况下,随着环境温度的升高,安全壳变形整体外扩,随着环境温度的降低,安全壳变形整体回缩。在工况1、2和4下穹顶竖向位移最大值位于穹顶中心附近,而在工况3下穹顶竖向位移最大值位于穹顶边缘靠近闸门一侧。在4种工况作用下,安全壳筒身水平径向位移和竖向位移最大值均位于设备闸门附近。

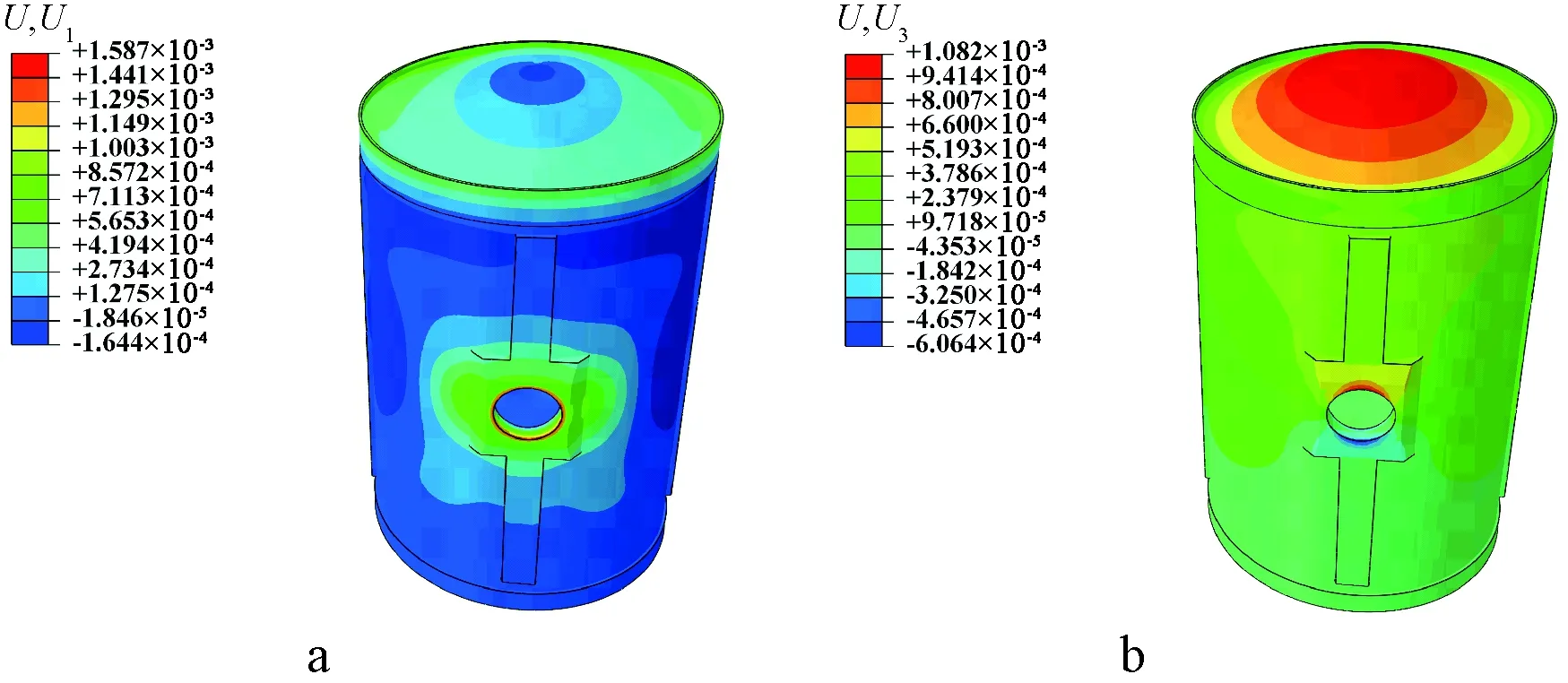
a—第104小时水平径向位移;b—第104小时竖向位移。图3 工况1下安全壳位移等值线云图 mFig.3 Contour cloud of containment displacement under the working condition one

a—第104小时水平径向位移;b—第104小时竖向位移。图4 工况2下安全壳位移等值线云图 mFig.4 Contour cloud of containment displacement under the working condition two

a—第104小时水平径向位移;b—第104小时竖向位移。图5 工况3下安全壳位移等值线云图 mFig.5 Contour cloud of containment displacement under the working condition three

a—第104小时水平径向位移;b—第104小时竖向位移。图6 工况4下安全壳位移等值线云图 mFig.6 Contour cloud of containment displacement under the working condition four

为研究上述4种工况下安全壳位移变化情况,分别选取了穹顶不同高程的2个点和筒身同一高程、不同方位的3个点,并输出其竖向位移和水平径向位移的时程曲线。图7为点位示意,A点位于穹顶中心外表面,B点位于穹顶360.5 gr方向,高程54.56 m处外表面,C、D、E点位于筒身高程26 m,方向分别为352.8,255.4,119.5 gr处外表面。

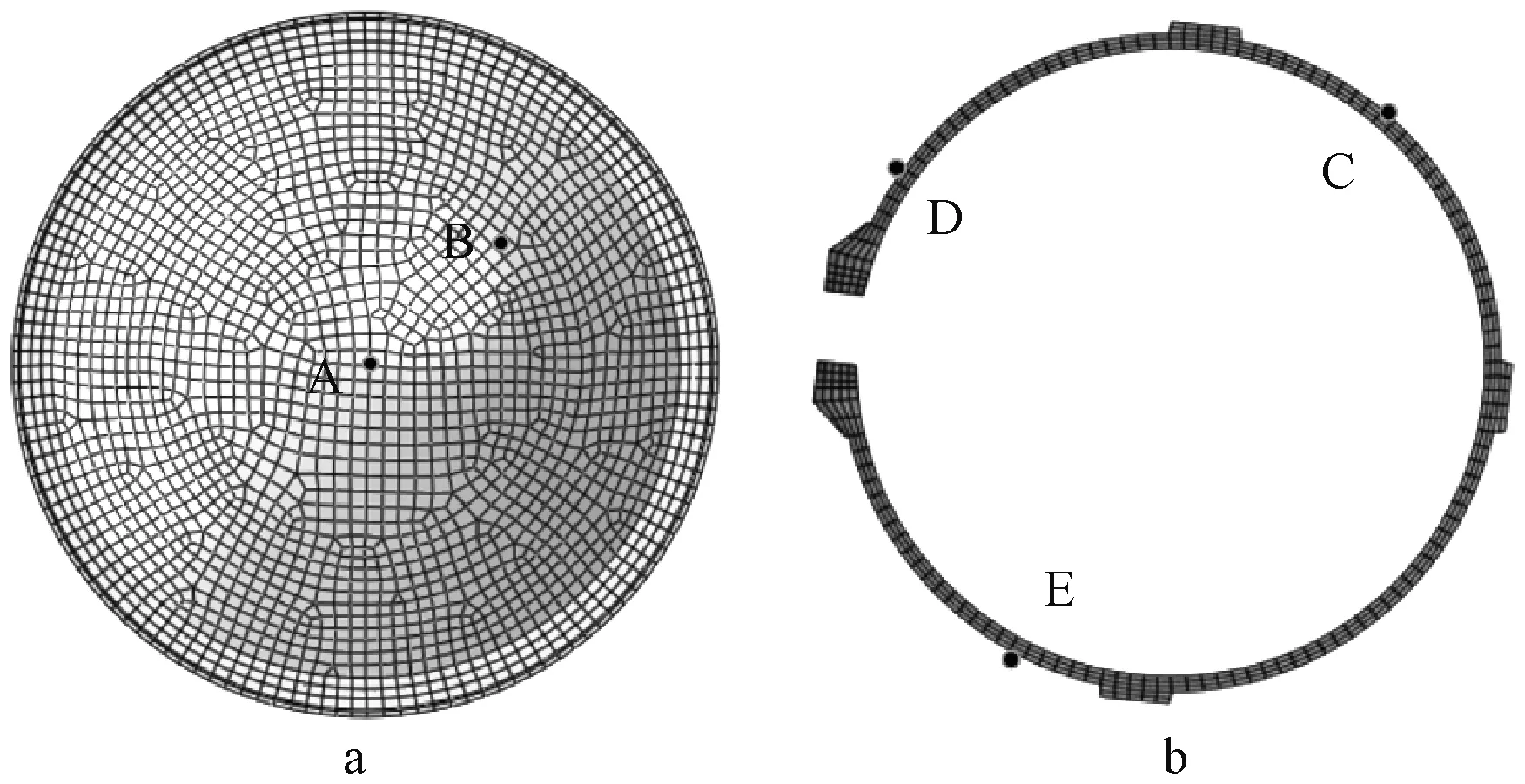
a—穹顶点位示意;b—筒身点位示意。图7 点位示意Fig.7 Point location schematic

图8为4种工况下穹顶A点竖向位移时程曲线。由图可知,3 d(上午10时至次日上午10时为1 d)后安全壳变形基本趋于平稳,初始温度场对结构变形的影响逐渐可忽略,故后续分析取第4～6天的数据进行各工况对比分析,以消除初始温度场对结构变形的影响[22]。

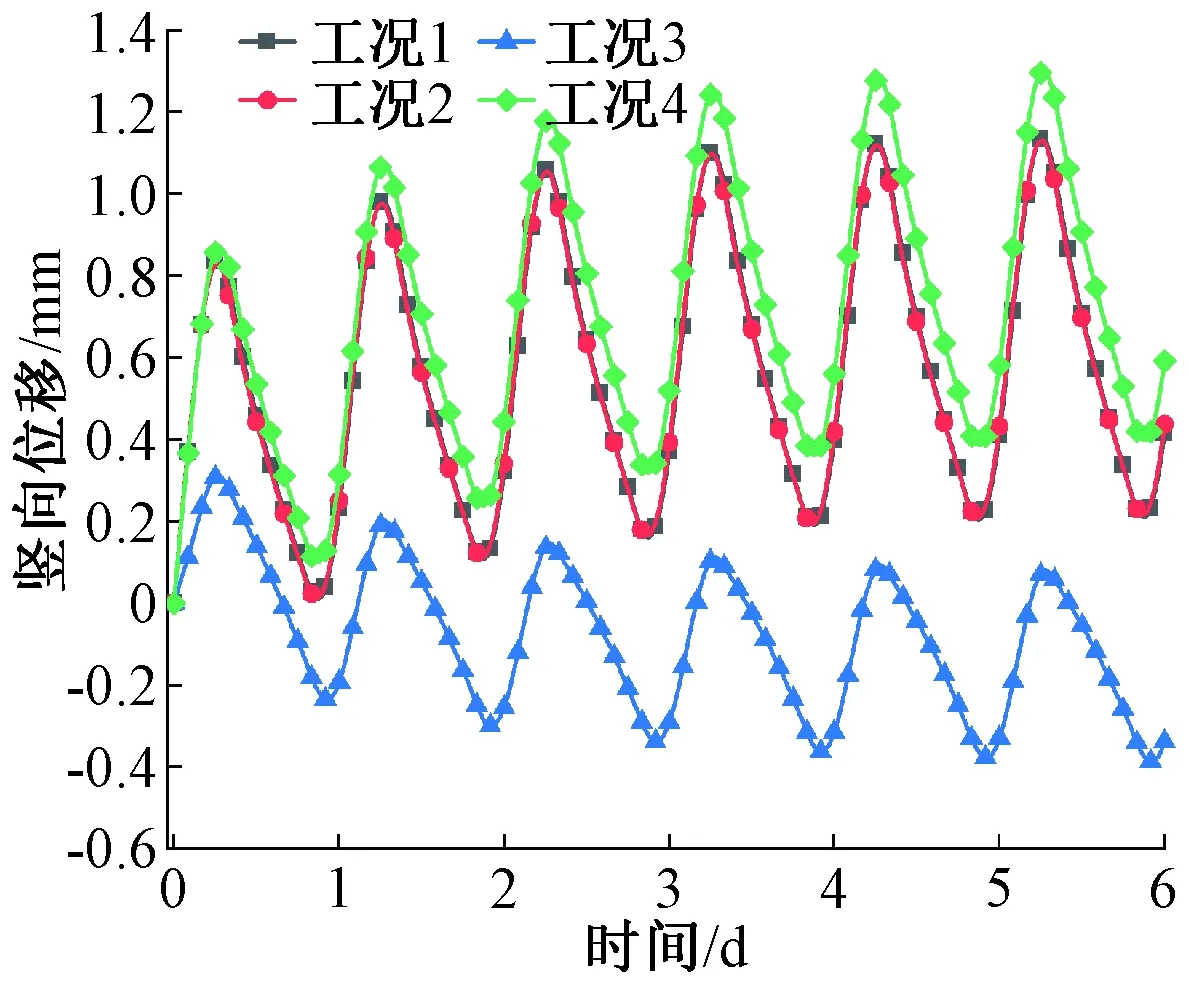
图8 4种工况下穹顶A点竖向位移时程曲线Fig.8 Time course curve of vertical displacement at point A of the containment dome under four working conditions

图9为4种工况下穹顶竖向位移时程曲线。由此可知,各工况下穹顶竖向位移随环境温度近似呈正弦曲线变化,且较环境温度变化滞后约2 h。工况1下穹顶A、B两点竖向位移平均幅值(波峰值与波谷值之差的一半)分别为0.459 mm和0.399 mm;工况2下穹顶A、B两点竖向位移平均幅值分别为0.454 mm和0.395 mm。上述两种工况下穹顶A、B两点竖向位移平均幅值相差不足1%。这说明不同热边界条件施加方法对穹顶位移的影响可忽略。有学者通过热边界分别施加法[11]或综合系数法[13-14]进行结构温度场研究,模拟结果均与实测值吻合良好。

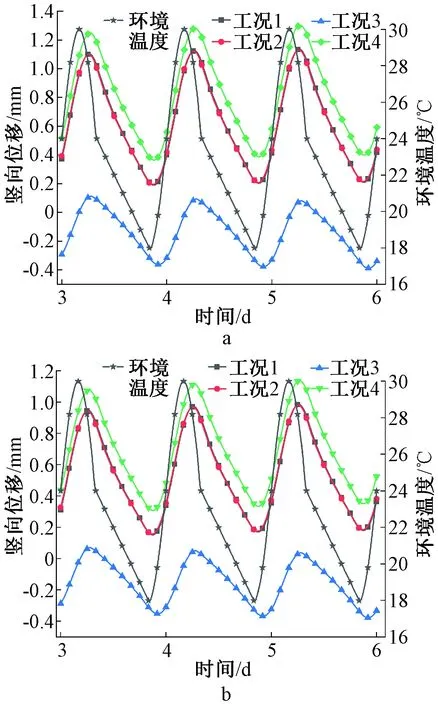
a—穹顶A点;b—穹顶B点。图9 4种工况下安全壳穹顶竖向位移时程曲线Fig.9 Time course curve of vertical displacement of containment dome under four working conditions

工况3下穹顶A、B两点竖向位移平均幅值分别为0.235 mm和0.208 mm,较工况1分别减小了49%和48%。这是由于工况3忽略了太阳辐射,导致穹顶竖向位移平均幅值较工况1大幅度减小。由此可知,太阳辐射是影响安全壳变形的主要因素,在计算时不可忽略。

工况4下穹顶A、B两点竖向位移平均幅值分别为0.444 mm和0.387 mm,与工况1相差约4%。这说明辐射换热是影响安全壳变形的次要因素,为了保证模拟的准确性,应在分析中考虑辐射换热对安全壳结构变形的影响[11-13]。

图10为4种工况下筒身水平径向位移时程曲线。同穹顶竖向位移变化规律相似,各工况下筒身水平径向位移随环境温度近似呈正弦曲线变化,较环境温度变化滞后约2 h。工况1下筒身 C、D和E点水平径向位移平均幅值分别为0.062,0.058,0.076 mm;工况2下筒身C、D和E点水平径向位移平均幅值分别为0.062,0.057,0.075 mm。因此,上述两种工况下筒身水平径向位移平均幅值几乎相同,与穹顶竖向变形规律一致,说明两种热边界施加方法对安全壳结构变形的影响可忽略。

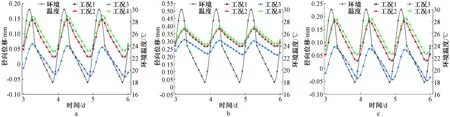
a—筒身C点;b—筒身D点;c—筒身E点。图10 4种工况下安全壳筒身水平径向位移时程曲线Fig.10 Time course curve of horizontal radial displacement of containment barrel under four working conditions

工况3下筒身C、D和E点水平径向位移平均幅值分别为0.049,0.046,0.060 mm,较工况1分别小21%、20%和21%。由于筒身忽略了太阳直射辐射,工况1和工况3的筒身水平径向位移平均幅值较穹顶竖向幅值有所减小,但太阳散射辐射和反射辐射对安全壳结构水平径向变形的影响仍较大,应在分析时予以考虑。

工况4下筒身水平径向位移平均幅值分别为0.058,0.054,0.069 mm,与工况1相差约9%,同样说明辐射换热对安全壳结构变形存在一定的影响。

综上,通过各工况的对比分析,说明安全壳位移随环境温度近似呈正弦曲线变化,环境温度和太阳辐射是影响安全壳变形的主要环境因素,辐射换热对安全壳变形的影响有限,不同热边界条件施加方法对安全壳变形的影响可忽略。

6 结 论

通过有限元数值模拟,研究了环境温度、太阳辐射、辐射换热以及不同热边界条件施加方法对安全壳变形的影响,阐明了预应力混凝土安全壳结构在综合环境因素下的变形规律,主要结论如下：

1)各工况下安全壳位移随环境温度近似呈正弦曲线变化,且较环境温度变化滞后约2 h。

2)太阳辐射、环境温度是影响安全壳变形的主要环境因素,应在安全壳结构整体性试验时予以考虑,以对变形测量结果进行合理的修正。当忽略太阳辐射时,穹顶竖向位移平均幅值降低了约49%,筒身水平径向位移平均幅值降低了约21%。

3)辐射换热对安全壳结构变形影响有限,是影响安全壳结构变形的次要环境因素,为提高模拟精度,建议考虑辐射换热的影响。

4)两种热边界条件施加方法对安全壳变形的影响可忽略,为了计算简便,可采用综合系数法进行施加。