伦敦色散力校正对含能分子晶体结构和弹性力学性能的影响

李怡薇,范晓静,魏 巍,韩旭辉,何春林,胡 涛,邵自强,陈 攀

(1.北京理工大学 材料学院,北京 100081;2.上海大学 材料科学与工程学院,上海 200444)

引 言

混合炸药在制备或经历冲击加载的过程中,含能分子晶体不可避免地发生形变,首先发生的是弹性形变[1]。了解弹性形变过程有助于进一步预测材料的力学响应和失效,因此弹性力学与材料的引爆和爆炸性能具有一定的相关性。同时,含能晶体的分子类型、晶体结构、微观结构和变形机制等共同决定动态压缩过程中对爆轰的感度。因此,了解弹性变形的微观机制,有助于提高其安全性,并调控含能材料的宏观性能。

能有效测试弹性张量的实验手段包括共振超声光谱(RUS)[2]、脉冲受激散射(ISS)[3]、布里渊散射[4]和纳米压痕技术[5]等,这些技术已应用于季戊四醇四硝酸酯(PETN)、六硝基六氮杂异伍兹烷(CL-20)、奥克托金(HMX)、黑索金(RDX)等。但由于各类含能分子晶胞类型不尽相同以及不同实验测试手段的局限性,导致所采集数据有限而不足以完整求解弹性张量。另外,含能材料由于其性质的特殊性,在进行实验时安全性能无法得到保证,样品的均一性和结晶度等很难统一,导致重复测试的可行性有待提高。而采用计算模拟获取弹性力学性质的方法可以减少危险性,缩短实验周期,具有可重复模拟、灵活性好和安全性高等特点。

当前主流的计算模拟方法主要包括第一性原理从头算、密度泛函理论法、半经验分子轨道方法以及分子力学(Molecular Mechanics: MM)和分子动力学(Molecular Dynamics: MD)[6]。Liu等[7]基于分子动力学(MD)模拟,对CL-20、HATO和FOX-7的晶体和分子结构、分子间相互作用和能量进行了预测和比较。Shi等[8]利用MM和MD方法研究了温度对CL-20、1-氨基-3-甲基-1,2,3-三唑硝酸盐(1-AMTN)晶体、CL-20/1-AMTN-共晶体以及混合物的力学性能的影响,结果表明,所有模型的力学性能在200～350 K之间都有明显的下降趋势,晶体的硬度、脆性和刚度都相应降低。

随着计算化学的发展,密度泛函理论(DFT)被广泛使用,结合不断优化的色散校正,DFT被认为是模拟凝聚态体系的黄金标准,也被用于典型含能分子晶体的弹性张量预测。本研究以CL-20、三氨基三硝基苯(TATB)和HMX三种典型含能分子晶体为研究对象,采用DFT定量化分子间非共价键相互作用,计算3种含能材料的弹性常数,并通过调控色散校正的施加和取消分析色散校正相互作用对HMX分子晶体的影响,揭示色散校正能对力学性能张量的影响规律,从而建立晶体结构与力学性能之间的关系,为实验工作提供重要的理论补充和实际指导。

1 计算方法

1.1 模型构建

密度泛函理论计算采用Quantum Espresso软件包[9]和VASP软件包[10]。依据X射线衍射或中子衍射的测试数据构建γ-CL-20[11]、TATB[12]和HMX[13]三种分子的晶胞结构。γ-CL-20和HMX晶胞属于单斜晶系,TATB属于三斜晶系,如图1所示。

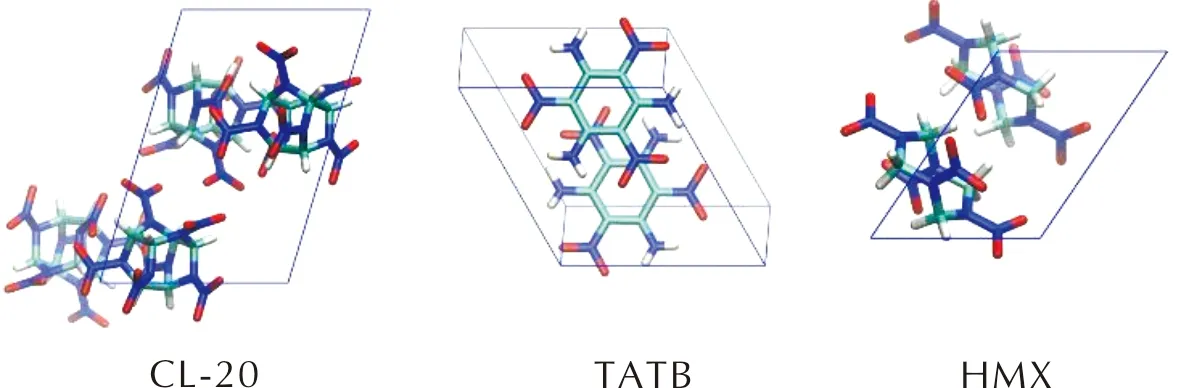
图1 CL-20、TATB和HMX的晶胞结构

1.2 IGM分析

采用Multiwfn[14]程序对周期性体系分子中的一个中心分子和周围分子的相互作用进行独立梯度模型(Independent gradient model, IGM)[15-16]分析。原子自由状态密度叠加构建的密度为准分子密度。将各个原子密度梯度直接加和得到准分子密度梯度为g(r),将各个原子密度梯度取绝对值再加和得到的准分子密度梯度gIGM(r)。二者求差,即为δg函数,δg(r)=gIGM(r)-g(r)[16]。IGM分析即利用δg函数直观地将原子间相互作用区域展现出来,原子间相互作用越强,相互作用区域的δg就会越大。IGM分析在计算时使用准分子密度方法(promolecular approach),只依赖原子坐标,不需要体系的波函数信息。输出结果明确包含片段间和片段内两组数据,因此在考察分子间相互作用时不会被分子内相互作用所干扰。在VMD[17]软件中可以将δg函数的等值面通过不同颜色投影展现出相互作用的类型和强度。绿色部分表示两个片段之间存在的短程范德华相互作用,而蓝色则代表作用力相对较强。

1.3 密度泛函理论计算

采用3种不同的色散校正方法(DFT-D2[18]、DFT-D3[19]和DFT-D4[20-21])进行密度泛函运算。能量收敛阈值和原子力收敛阈值分别设置为1.0×10-6Ry和1.0×10-5Ry。K点设为2×2×2×0×0×0。采用不同的波函数动能截断对3种含能分子进行优化,依据能量收敛情况确定截断动能,CL-20的波函数截断动能设为160 Ry(1 Ry=1 312.7 kJ/mol),TATB和HMX的波函数截断动能设为140 Ry。

1.4 能量分解

能量分解分析(Energy decomposition analysis:EDA)一般可根据超分子方法求取(Supramolecular approach),即二聚体之间的能量等于二者的总能减去各自单体的能量(ΔE=EAB-EA-EB)。根据经典力学,分子间非共价键相互作用(Etotal)可划分为静电相互作用(Eelec)和范德华力相互作用(Evdw)(伦敦色散相互作用Edisp+泡利互斥作用EPauli):

Etotal=Eelec+Evdw

(1)

Evdw=Edisp+EPauli

(2)

可将Pauli互斥作用囊括在静电力中,其总和仍称之为静电相互作用,因此除去Pauli相互作用的范德华力可以被认为是色散作用Evdw=Edisp,分子间相互作用可以被认为由位能和色散作用组成。

Eelec=Eelec+EPauli

(3)

Etotal=Eelec+Edisp

(4)

而在密度泛函理论中,能量的组成比较复杂,包括核核斥能、核电子吸引能、经典电子库仑排斥、动能和交换能等,将色散力之外的分子间相互作用统称为位能Ester,则能量的表达式为:

Etotal=Ester+Edisp

(5)

但为求简洁,本研究仍将位能称为静电作用。静电和色散作用分别可以划分为分子内(intra)和分子间(inter)相互作用,即静电作用由分子内静电作用(EintraE)和分子间静电作用(EinterE)组成,色散作用由分子内色散作用(EintraD)和分子间色散作用(EintraD)组成,则分子间总的非共价相互作用等于以上4项能量的总和:

Eelec=EintraE+EinterE

(6)

Edisp=Evdw=EintraD+EinterD

(7)

Etotal=EintraE+EinterE+EintraD+EinterD

(8)

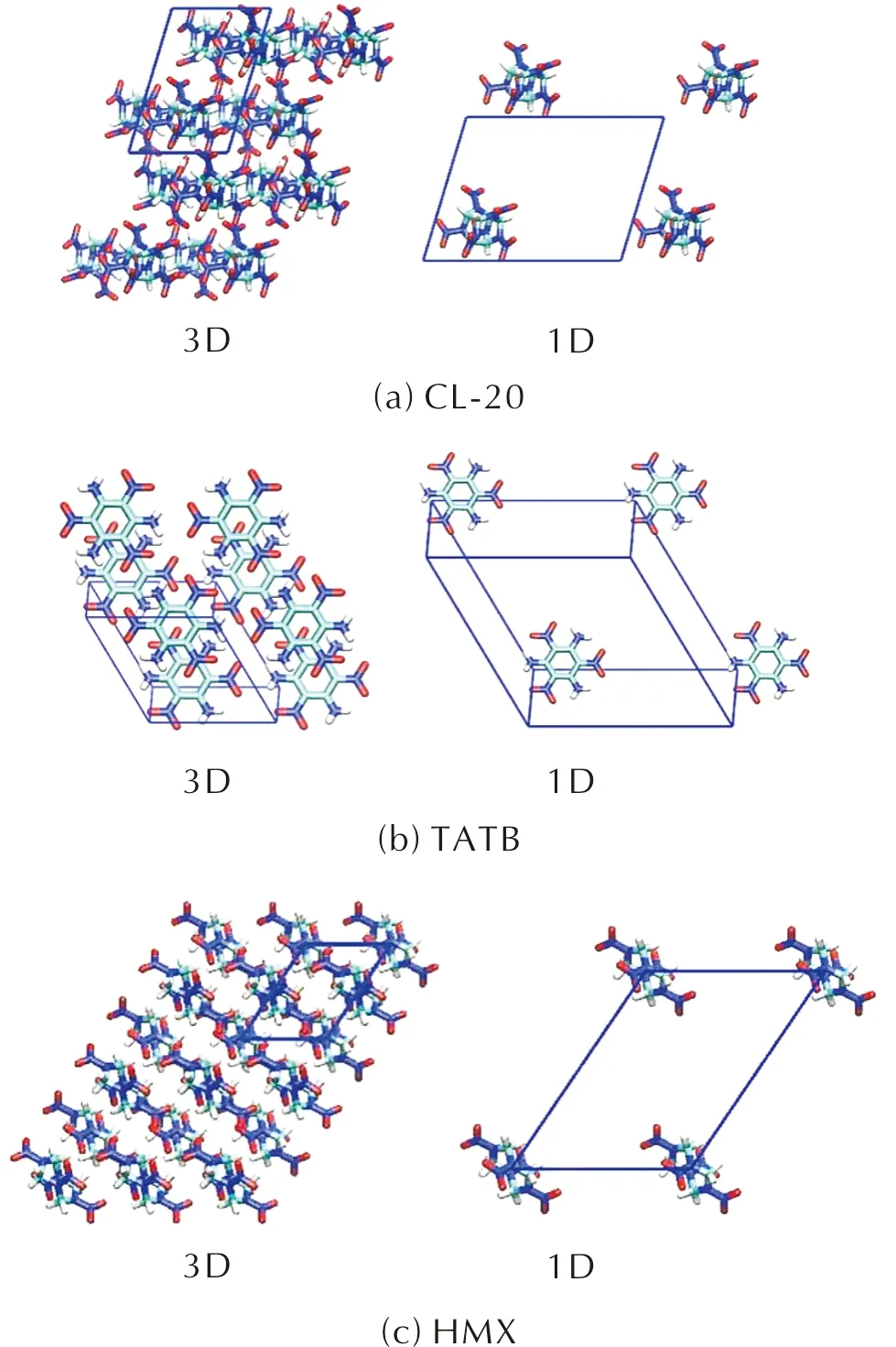
图2 CL-20、TATB和HMX非共价键相互作用能计算使用的“凝聚态”(3D)和“孤立态”(1D)

(9)

(10)

(11)

(12)

根据公式(11)和(12)可知分子内色散力等于:

(13)

由公式(9)、(10)和(13)可知分子间色散力为:

(14)

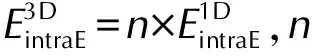
(15)

分子的内聚能为:

(16)

由此可以求取分子间不同属性的非共价键相互作用。变换不同的色散校正方法(D2、D3和D4),便可以得到基于不同色散校正方法的各项分子间相互作用。

1.5 弹性张量

固体在拉格朗日弹性理论中可以被视为均匀且各向异性的弹性介质[22]。其中拉格朗日应变η、应力τ的定义如下[23]:

(17)

τ=det(1+ε)(1+ε)-1·σ·(1+ε)-1

(18)

式中:ε为应变张量;σ为应力张量,由晶体总能量E的微分可将σ定义为:

(19)

式中:V为晶体体积。在线性范围内,拉格朗日应力和应变满足广义胡克定律:

(20)

式中:Cαβ是晶体的弹性常数,为四阶弹性张量的分量。同时,晶体总能量可以用应变的幂级数η表示为:

(21)

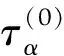
根据公式(20)和(21)可知弹性常数有两种表达方式,本研究选择能量-应变法计算弹性常数[23],即:

(22)

表1列出了在能量应变法中使用的29种变形类型[21], 每种变形类型为(xx,yy,zz,yz,xz,xy)六个方向的组合或独立变形。不同晶系所采用的应变变形组合类型不同,单斜晶体有13个弹性常数,采用η(1)、η(3)、η(4)、η(5)、η(6)、η(7)、η(12)、η(20)、η(24)、η(25)、η(27)、η(28)和η(29)共13种应变变形组合,三斜晶体含有21个弹性常数,采用η(2)、η(3)、η(4)、η(5)、η(6)、η(7)、η(8)、η(9)、η(10)、η(11)、η(12)、η(13)、η(14)、η(15)、η(16)、η(17)、η(18)、η(19)、η(20)、η(21)和η(22)共21种应变变形组合。对于每组应变变形,优化5种变形体,拉格朗日应变的最大绝对值设为0.01,即应变幅值在-0.01～0.01之间。采用DFT和色散校正方法[18-21]对每种应变变形进行能量最小化。用二阶多项式对能量E和拉格朗日应变η之间的函数关系进行拟合,其结果拟合为抛物线函数,如图3(a)所示。求其二阶导数并除以晶胞体积V,将计算结果记为a。以单斜晶系为例,采用Elastic程序[21]结合计算结果a对图3(b)中的线性方程组求解得到对应晶系的弹性常数,图3(c)展示了求解二阶弹性常数的计算流程图[23]。采用VMD软件[17]、ELATE软件[24]、Anisotropic calculator程序[25]和 PARAVIEW软件[26]对分子结构和计算结果进行可视化。

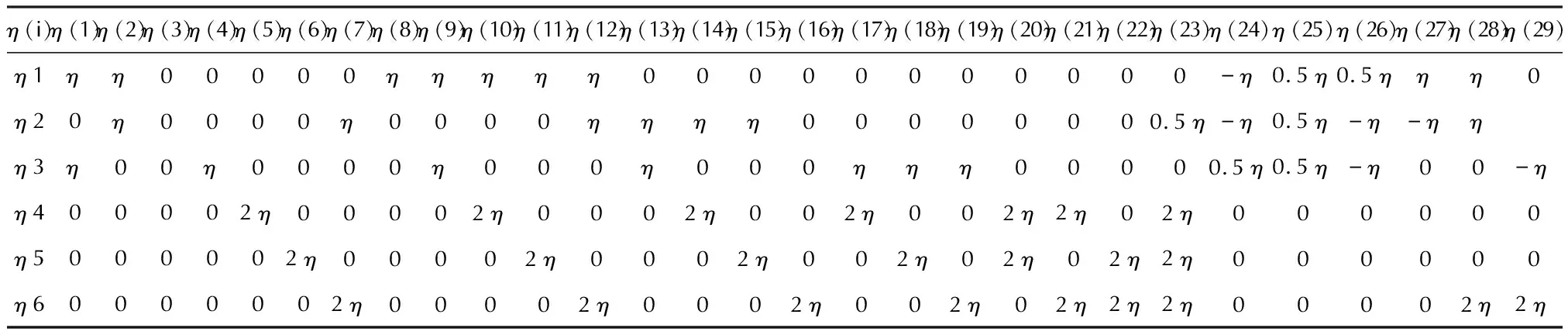
表1 用Voigt符号表示的在能量应变法中使用的29种变形类型[23]

图3 (a)HMX分子在晶胞(bc)方向上的能量-应变曲线及其拟合;(b)单斜晶胞弹性张量的线性求解方程;(c)以单斜晶系为例,求解二阶弹性常数(SOECs)的计算流程图[23]

2 结果与讨论

2.1 晶胞参数

表2为实验和DFT计算所得的CL-20、TATB和HMX的晶胞参数。当施加不同的色散校正方法时,含能分子的晶胞参数略有差异,但与实验值的平均偏差均在2%以内,其中使用D2色散校正方法计算得到的参数平均偏差最小,D4其次。当色散校正取消时,含能分子的晶胞参数和晶胞体积增加,明显偏离实验值,体积偏差超过17%,说明没有色散校正相互作用,含能分子的堆积比较松散,密度较小。DFT-D2是在常用交换关联泛函如PBE的基础上增加了额外半经验能量用于校正色散相互作用。DFT-D3为了避免重复计数问题,使用阻尼函数如零阻尼或BJ阻尼来调节色散校正在原子周围近、中程距离时的行为,考虑了电子极化。DFT-D4进一步改进,让原子色散系数与原子电荷挂钩,考虑了实际电子结构,能自适应地根据原子周围的电荷分布调整优化实时诱导偶极色散力系数,使用的是BJ阻尼函数[19-20]。

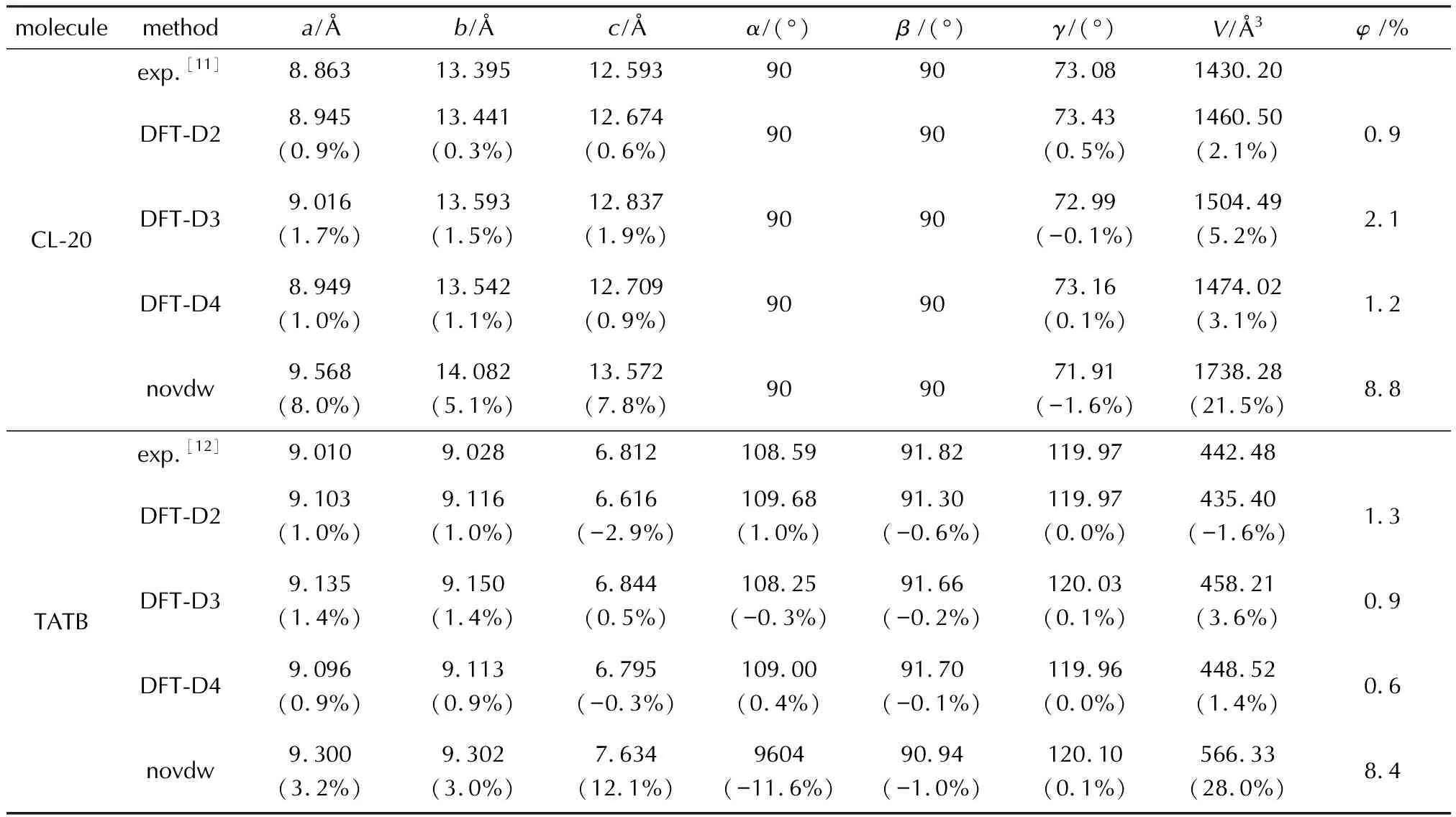
表2 调控色散相互作用所得的3种含能分子的晶胞参数和体积以及与实验值的相对偏差

2.2 能量分解

图4分别展示了CL-20、TATB和HMX的分子间非共价键相互作用力,3种含能分子均存在较强的范德华相互作用(绿色部分)。

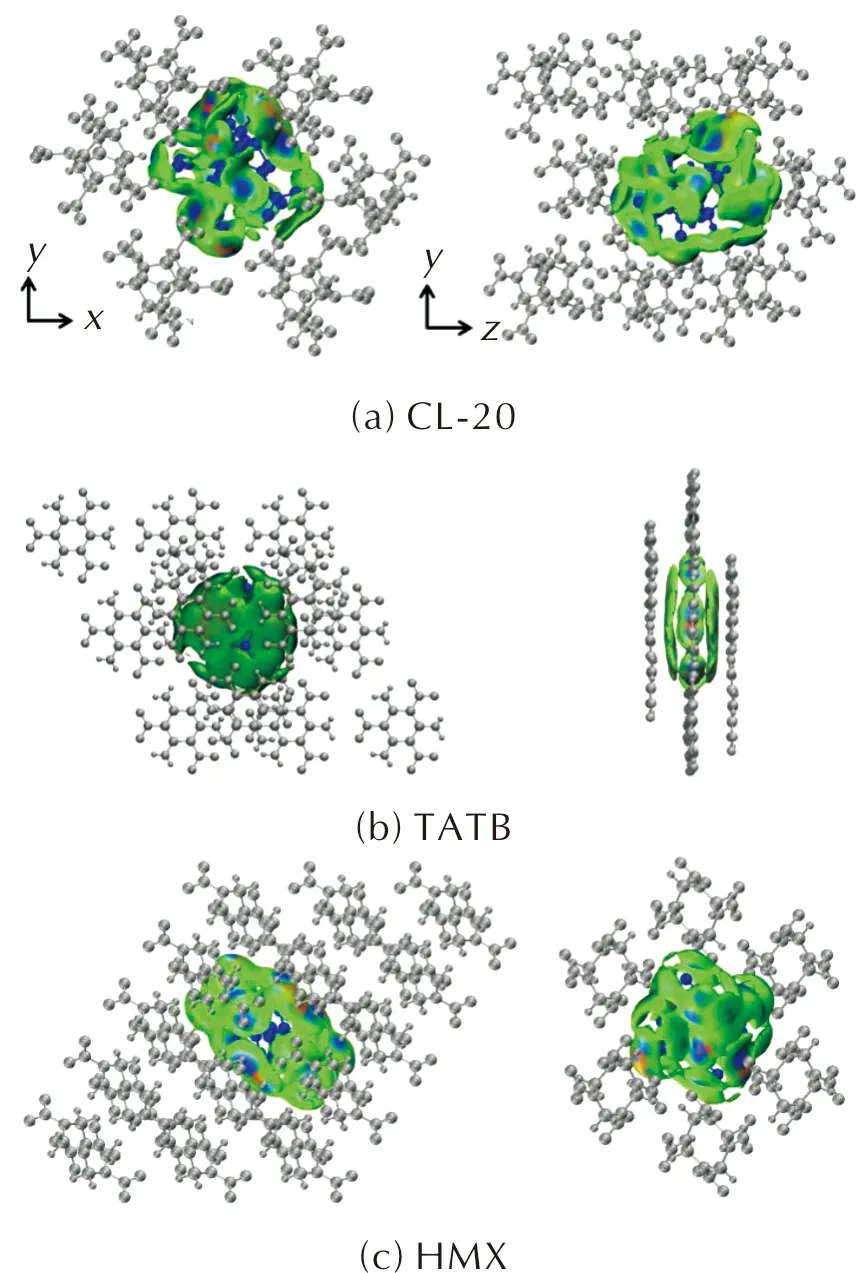
图4 基于IGM的3种含能分子的分子间相互作用图

表3为3种含能分子关于分子内色散能(intra_disp)、分子间色散能(inter_disp)、分子间静电能(inter_elec)和分子内聚能(E_cohesion)的能量分解结果。对于CL-20分子,当施加D2色散校正时,其分子内色散能为-134 kJ/mol,分子间色散能为-118 kJ/mol,而分子间静电能仅为-24 kJ/mol,分子内色散力和分子间色散力大约是分子间静电力的4.9倍或5.5倍。对比D2和D3色散校正方法,分子内色散能和分子间色散能也均大于分子间静电能。TATB和HMX的情况也是如此,无论采用哪种色散校正方法,均能观察到含能分子的分子间校正色散力大于分子间静电力,说明色散力校正对分子结构的凝聚起到主导作用。但当含能分子使用D3色散校正时,其分子内色散能和分子间色散能均略小于对应的使用D2色散校正计算出的结果,分子间静电能则稍大于使用DFT-D2色散校正计算出的结果,这主要是因为D3的色散校正能小于D2,所重现的晶体结构没有D2堆积的紧密(比较图2的体积可以看出),因此静电排斥效应较弱,静电能相对稍强。当含能分子使用D4色散校正时,以CL-20分子为例,分子内色散能为-174 kJ/mol,大约是使用D2和D3计算出的分子内色散能的两倍,分子间色散能和分子间静电能的结果与使用D3计算出的结果较为相近。

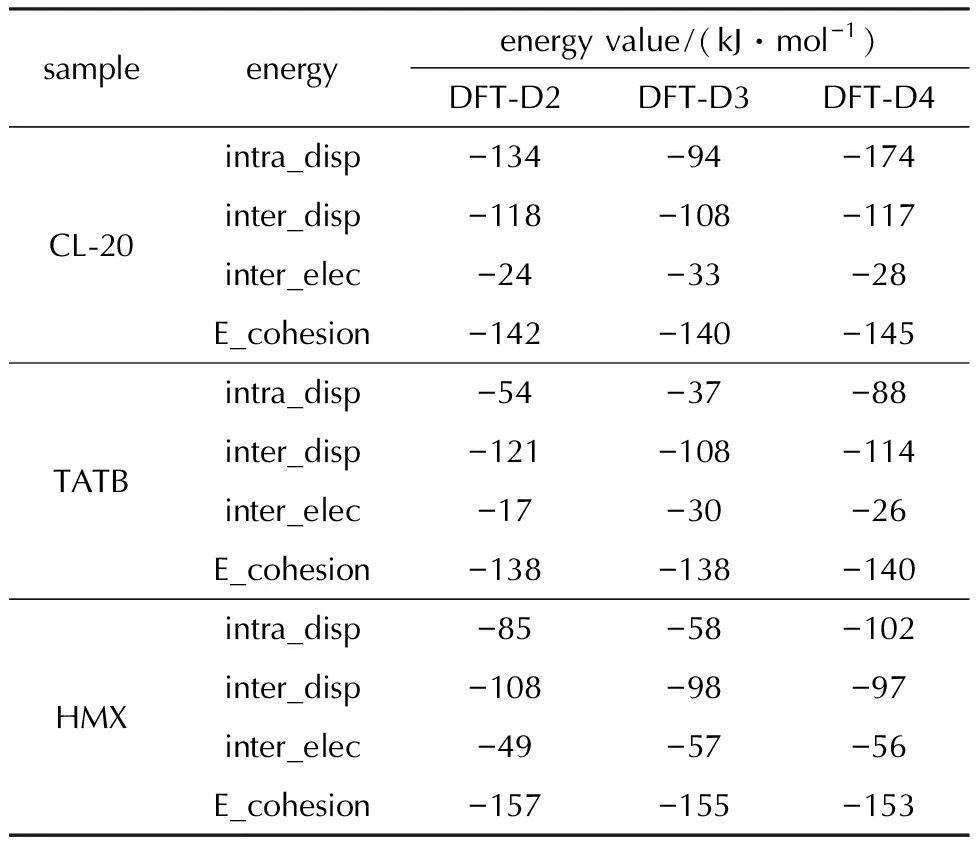
表3 3种含能分子关于分子内色散力(intra_disp),分子间色散力(inter_disp),分子间静电力(inter_elec)和分子内聚能(E_cohesion)的能量分解结果

因此可以发现,对于含能分子,使用不同色散校正方法预测的同一种分子间作用力,由D2计算得到的结果会明显大于D3和D4,分子间静电能则相反,D2得到的结果最小,D3和D4计算出的分子间色散校正能和分子间静电能结果较相近,但D4计算的分子内色散能大约是DFT-D3计算出的分子内色散能的两倍。对于同一种含能分子,采用不同色散校正方法测得的分子内聚能比较接近。总之,不同色散校正方法之间存在一定差别。这说明当考虑实际情况中电子云的极化效应,分子间色散作用减小,而分子内静电作用则变大,但分子间色散相互作用主导含能分子聚集的结论不变。

2.3 弹性常数及色散力的影响

2.3.1 γ-CL-20

γ-CL-20晶体属于单斜晶系,具有13个弹性常数。表4是利用DFT-D2色散校正计算出的CL-20的弹性常数。表5是基于Voight-Reuss-Hill表示法[26-28]近似计算出的体模量(K)、杨氏模量(E)、剪切模量(G)和泊松比(ν)。基于Hill表示法计算的模量值介于基于Reuss和Voigt表示法测定的模量值之间,与前人的研究结果一致[29]。与Haycraft等[4]利用布里渊散射法测定的CL-20的弹性常数相比,a轴对应的拉伸常数C11和剪切常数C44与实验值的偏差较大,对此暂时无法解释,但这与Hooks等[1]使用DFT-D3的计算结果一致。其他弹性常数以及各种模量与实验值呈现出较好的一致性。利用ELATE软件[23]对CL-20的弹性性质进行3D可视化分析,得到弹性常数随晶体方向而变化的表面轮廓图以及xy、xz和yz平面上杨氏弹性常数的二维投影,如图5所示。根据表4的数值和图5的表面轮廓图,可知CL-20晶体在xy和yz平面内各向异性的程度相对较低。

表4 CL-20在施加D2色散校正下的弹性常数以及实验值[4]

表5 CL-20基于Voight-Reuss-Hill(V-R-H)表示法[26-28]近似计算出的体模量(K)、杨氏模量(E)、剪切模量(G)和泊松比(ν)以及实验值

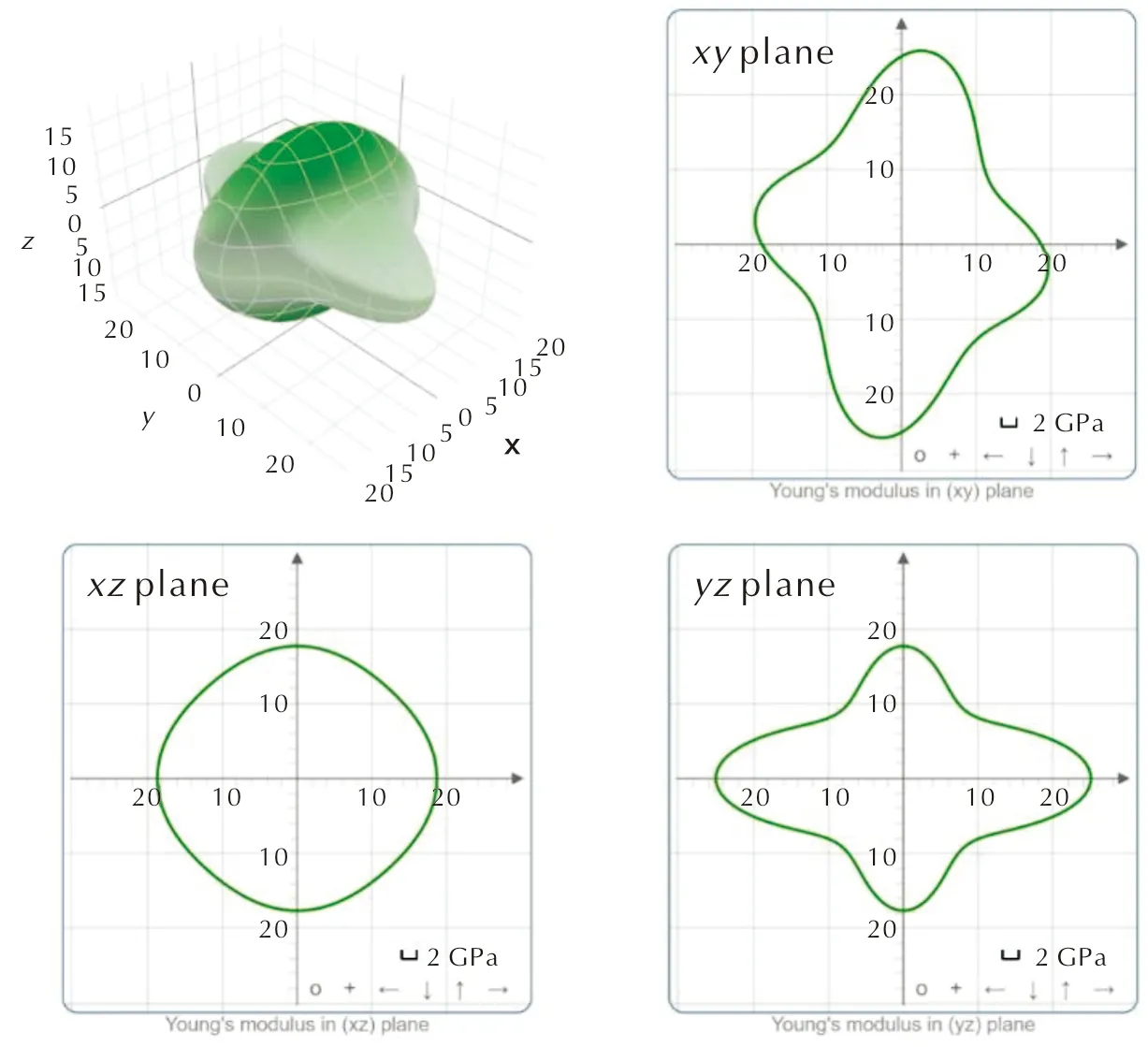
图5 CL-20在施加D2色散校正下的弹性常数随晶体方向而变化的表面轮廓图及在xy、xz和yz平面上的二维投影

2.3.2 TATB

表6显示了TATB在D2色散校正方法下的弹性常数。表7是基于Voight-Reuss-Hill表示法[27-29]近似计算出的TATB的体模量(K)、杨氏模量(E)、剪切模量(G)和泊松比(ν)。目前尚未有TATB分子弹性常数的实验数据。图6是TATB的弹性常数随晶体方向而变化的表面轮廓图及不同平面上的二维投影,可以观察到TATB分子a轴和b轴方向上的弹性常数比较接近,明显大于c轴的弹性常数,同时也大于HMX和CL-20对应的弹性常数,呈现出非常明显的各向异性特性。微观结构决定宏观性质,TATB晶体有点“类似”石墨、纤维素、凯夫拉等的层状结构,鉴于其分子呈现扁平特征,在每一层内部存在着分子内和分子间氢键相互作用以及范德华力[30],层和层之间没有氢键作用,主要依靠范德华力堆积,图4的分子间相互作用图也可以证实。TATB分子内和分子间氢键的存在是造成其感度较低的主要原因[31]。图7展示了TATB在不同平面内的结构投影,可以观察到c轴方向上没有氢键作用,仅存在范德华力,而由于氢键具有方向性,a轴和b轴方向上同时存在着氢键和范德华力。因此a轴和b轴方向上分子间相互作用明显大于c轴方向,使得C11和C22大于C33,而D2的预测结果大于D3则是由于D2的色散校正大于D3。从图7中还可以观察到在yz平面和xz平面内没有氢键的存在,而在xy(晶胞ab)平面内存在氢键,因此xy平面上的剪切模量要大于yz平面和xz平面的剪切模量,即C66大于C44和C55,分别为28 GPa、1.7 GPa和1.4 GPa。

表6 TATB在施加D2色散校正下的弹性常数以及参考值[32]

表7 TATB基于Voight-Reuss-Hill(V-R-H)表示法[27-29]近似计算出的体模量(K),杨氏模量(E),剪切模量(G)和泊松比(ν)

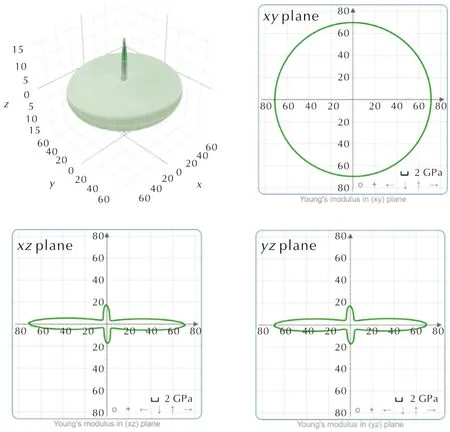
图6 TATB在施加D2色散校正下的弹性常数随晶体方向而变化的表面轮廓图及在xy、xz和yz平面上的二维投影

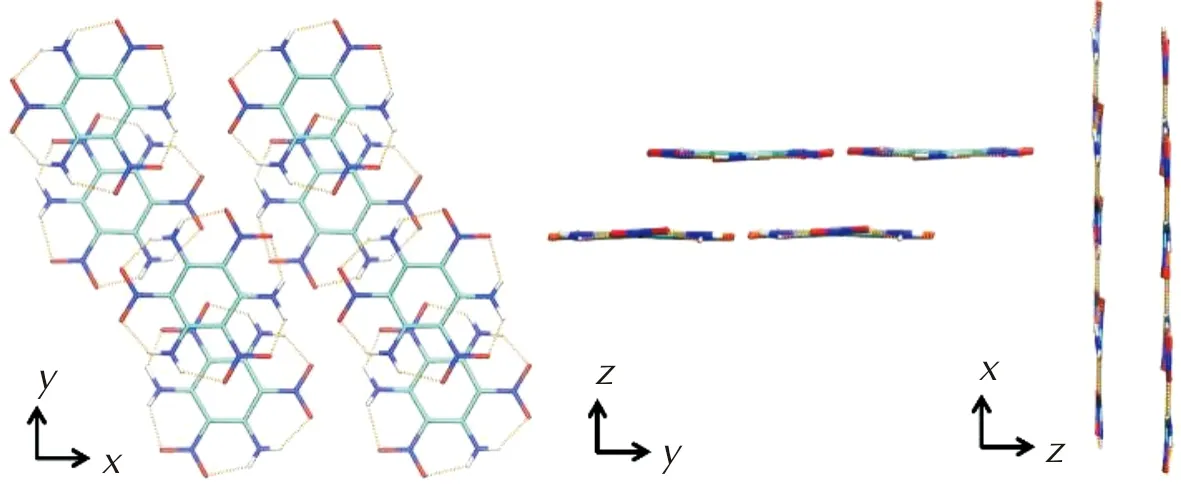
图7 TATB在不同平面内的结构投影

2.3.3 HMX

表8显示了HMX在施加D2、D3和D4色散校正方法下和取消色散校正时的弹性常数。与多组实验[33-35]和Fedorov等[32]的模拟进行了比较,其结果较为一致,差异大小主要取决于使用的色散校正方法。由表2可知,利用D3色散校正优化出的HMX的晶胞体积最大,利用D2色散校正优化出的晶胞体积最小。根据计算公式(22)可知弹性常数与晶胞体积成反比,因此使用D3计算的弹性常数最小,而D2计算出的值最大,正如表8所显示的结果。D2的弹性常数计算结果略高于实验数据,D3和D4预测的模拟值与实验值的吻合度更高。表9是基于Voight-Reuss-Hill表示法[27-29]近似计算出的HMX的体模量(K)、杨氏模量(E)、剪切模量(G)和泊松比(ν),与实验值相比[36],D3和D4计算出的模量与实验值的一致性较好。图8是HMX在D2色散校正下的弹性常数随晶体方向而变化的表面轮廓图及在xy、xz和yz平面上的二维投影,可知HMX晶体在弹性力学上的各向异性程度也较低。

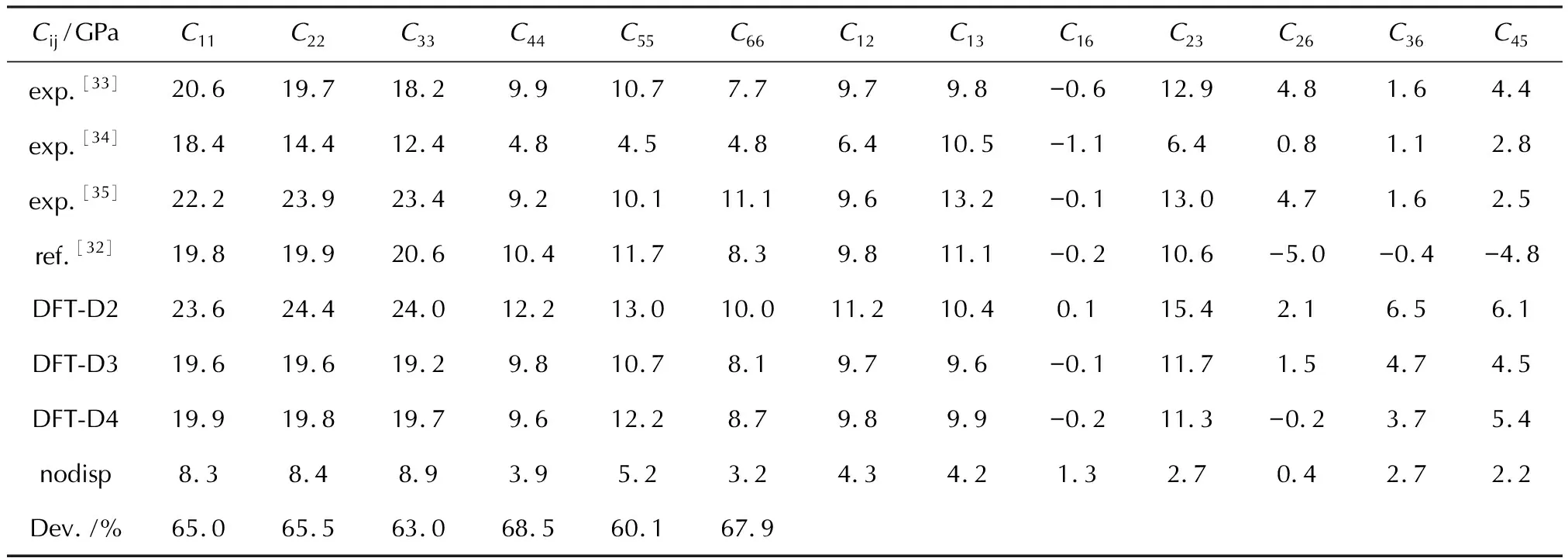
表8 HMX在施加D2、D3和D4色散校正和取消色散校正时的弹性常数及参考值[33-35],和取消色散校正时的弹性常数相较于D2计算结果的差值百分比(Dev.)

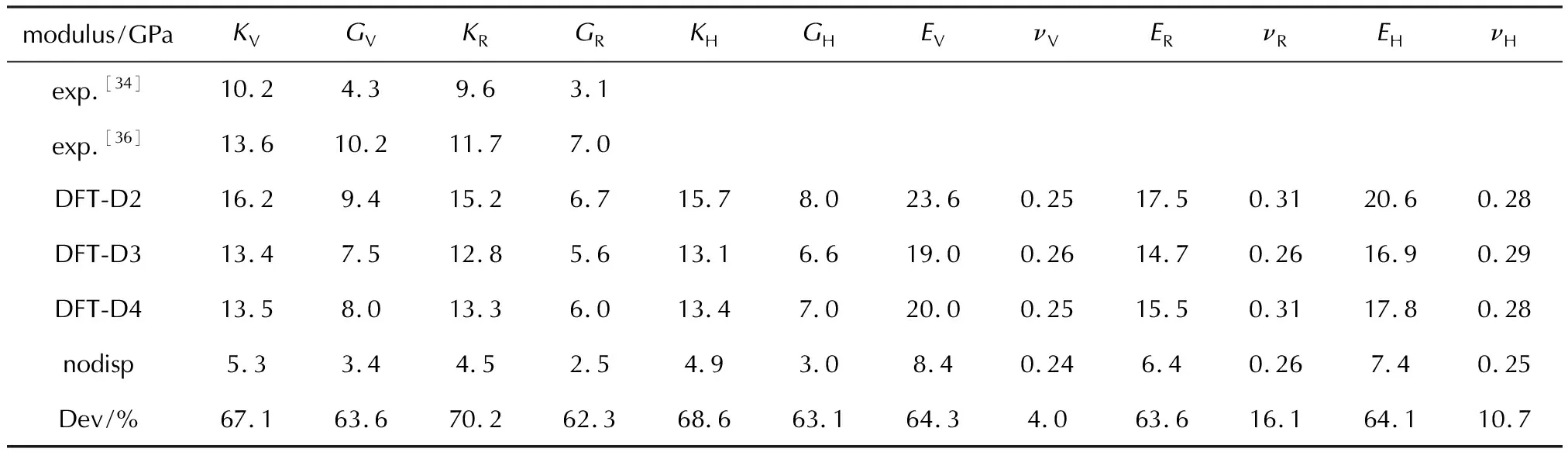
表9 HMX基于Voight-Reuss-Hill表示法近似计算出的体模量(K),杨氏模量(E),剪切模量(G)和泊松比(ν)以及实验值,和取消色散校正时的模量相较于D2计算结果的差值百分比(Dev.)[27-29,34,36]

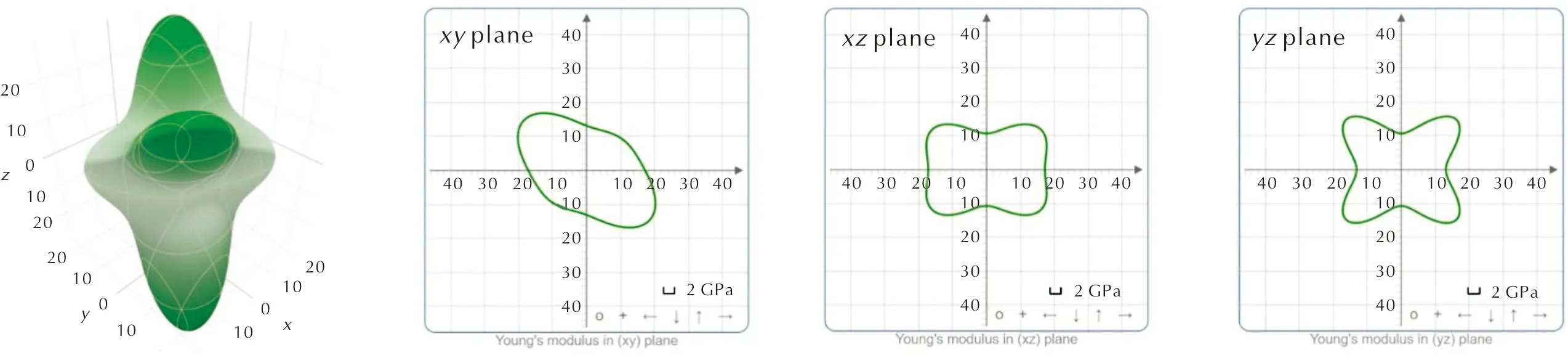
图8 HMX在施加D2色散校正下的弹性常数随晶体方向而变化的表面轮廓图及在xy、xz和yz平面上的二维投影

为定量比较CL-20、TATB和HMX弹性各向异性的程度,根据以下公式[37]对3种含能分子晶体的各向异性指数AU进行了计算:

(23)

式中:GV和GR分别是基于Voight表示法和Reuss表示法计算出的剪切模量;KV和KR分别是基于Voight表示法和Reuss表示法计算出的体模量。CL-20、TATB和HMX在采用D2色散校正下的AU分别为0.7、19.8和2.1,可知TATB的各向异性程度最大,其次是HMX,各向异性程度最小的是CL-20。与各含能分子晶体根据表面轮廓图推测出的结论一致。

当色散校正取消后,所有晶体的体积变大,分子结构变得松散,力学性能减小,弹性常数和模量明显降低,和D2计算的值相比,HMX所有方向平均下降了65%左右。其中体积在色散校正取消后增加了17.8%,如表2所示,以应变变形组合η(20)为例,能量-应变系数a在色散校正取消后了下降57.2%,如图9所示。

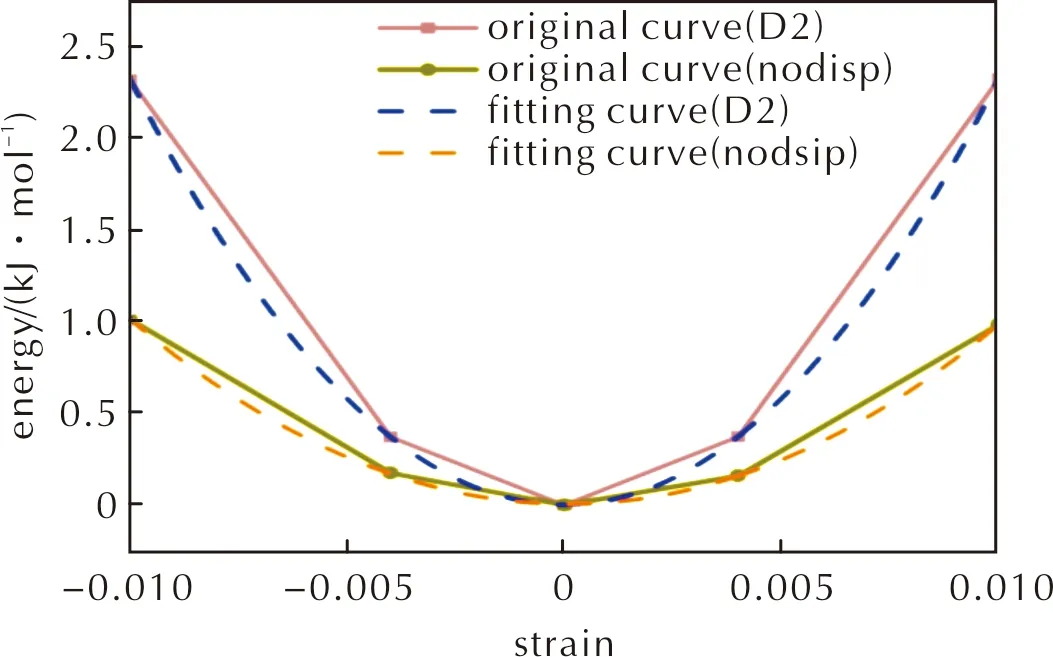
图9 HMX的应变变形组合η(20)分别在施加D2色散校正和取消色散校正时的能量—应变曲线及拟合曲线

图10是HMX分子在施加D2色散校正(网格轮廓)和取消色散校正(实面轮廓)时的弹性模量3D图。由图10可以更加直观地观察到当色散校正取消后弹性模量的下降幅度,说明色散校正能对力学性能的影响十分重要。

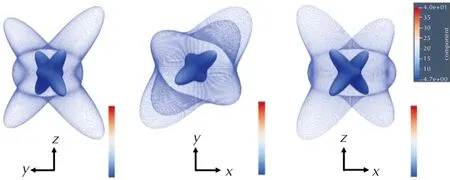
图10 HMX分子在施加D2色散校正(网格轮廓)和没有色散校正(固体轮廓)时的弹性模量3D表示图

3 结 论

(1)采用不同色散校正方法计算3种含能分子的分子间相互作用力,观察到晶体之间的分子间色散力大于分子间其他非共价键相互作用,说明色散力对分子的凝聚和结构稳定性起主导作用。

(2)与DFT-D2相比,DFT-D3和DFT-D4计算出的弹性常数与实验值的平均偏差较小,体现出电子极化作用的重要性。模拟所得的3种含能分子的弹性常数中,TATB最大,HMX和CL-20接近,这主要是由于TATB分子中各向异性的氢键结构所导致。相较之下,TATB晶格最“坚硬”,CL-20其次,HMX最小。TATB较高的弹性模量说明其分子较难发生弹性变形,引起爆炸变化所需的激发冲量则会相对较高,因此TATB的感度较低,符合“晶格越硬,流体力学冲击引发的引爆起爆感度越钝”理论[38]。

(3)使用具有色散校正的密度泛函理论可以确定具有不同晶胞对称性的分子晶体的弹性常数,理论和现有实验弹性常数之间有合理的一致性。这些弹性张量数据可以用于将来发展含能分子的塑化模型,在新的合成含能材料的弹性性质研究方面具有一定的应用价值。

(4)通过施加和取消色散校正对比HMX分子的弹性模量,发现色散校正能在含能晶体中的分子堆积起着关键作用,对含能分子晶体力学性质的贡献不可忽视。有助于理解含能材料的力学性质和结构-性能关系,对含能材料的应用控制和安全性的提高具有重要意义。

(5)弹性变形作为含能材料机械变形的初始阶段,具有重要的研究价值。大量实验和模拟方法开发致力于研究含能材料分子晶体的弹性性质,相比于基于经验力场的分子动力学模拟方法,密度泛函理论在准确度方面具有一定的优势,但和模拟数据和实验之间的差异也需要考虑温度、压力、零点振动、非谐性、动力学等物理效应。因此,将来有必要使用考虑(加载温度和压力效应)第一性原理的分子动力学模拟方法研究含能晶体的弹性性质,并适当考虑缺陷、表面等结构在经历形变时所产生的“力学热点”效应。