响应面优化电芬顿法降解印染废水工艺研究

林继辉,谢冰冰,周梦婷,马戎,戴玉梅

(闽南科技学院,福建 南安 362332)

印染工业从诞生以来经过了快速的发展,带来了巨大的经济效益,但是伴随快速发展与其巨大的经济效益的同时带来的环境污染也不可忽视,其中以印染行业排放的污水污染最为严重[1-2],其污水具备成份复杂(大多数有毒难降解的有机物)、较深的色度、在高酸碱度的同时还常含有难用常规生物方法进行处理的偶氮型染料[3-4],是一种难以使用传统的生化、物化方法处理的工业废水[5-6]。

阴极电芬顿法是近些年来新兴的一种髙级电化学氧化技术(Advanced Oxidation Process,简称AOPs)[7],它是在芬顿试剂的基础上加入电化学的方法进行改良的新型降解方法。其原理是利用电化学的方法将混合体系中的溶解氧(O2)扩散至阴极表面,在阴极表面发生还原反应形成过氧化氢(H2O2)并与溶液中的亚铁离子(Fe2+)发生芬顿反应,生成强氧化性的羟基自由基(·OH)进而氧化降解废水有机物[8-9]。阴极电芬顿法可以显著降低药剂费用[1-2]、提高反应速率并且在有效降解有机物的同时还可以避免降解过程中产生的氢氧化铁(Fe(OH)3)污泥带来的污染[10],相比于传统的芬顿法它具有处理效率高、过程控制简单、应用广、对废水pH要求宽和环境友好型等优点,是一种绿色环保的水处理方法。

响应面法(Response Surface Methodology,RSM)是一种解决多变量问题的最有效的统计方法,它将数学方法和统计方法相结合建立连续变量曲面模型[11],经常用于分析某个响应值受多种因素影响的分析和建模问题,评价响应值与各因素之间的交互作用,最终确定最佳水平范围以此达到优化响应值的目的。

文中采用不锈钢为阳极(由于采用普通铁板时容易在阳极周围产生过量的Fe3+)、多孔钛网电极板为阴极、外部投加 H2O2、Fe2+的电芬顿装置处理亚甲基蓝模拟废水,以降解率为评价指标,重点考察通电时间、pH、亚铁离子和过氧化氢投放量、电流强度(I)5个因素对其降解率影响。利用响应面(RSM)设计原理,以上述5因素为因变量、亚甲基蓝模拟废水降解率为响应值,以获得阴极电芬顿法的降解亚甲基蓝模拟废水的最优工艺参数。希望能给印染废水处理行业提供经济,高效的理论技术参考。

1 材料与方法

1.1 仪器及试剂

PS-305D直流稳压电源 深圳怡展仪器有限公司;PHS-3C pH计 上海仪电科学仪器股份有限公司;DLAB移液枪(100～1 000 μL);UV756(CRT)紫外分光光度计 上海昕瑞仪器仪表有限公司;DFS-101S集热式恒温加热磁力搅拌器 郑州长城科工贸有限公司;EL104电子天平 梅特勒-托利多(上海)仪器有限公司。硫酸钠、30%过氧化氢、氢氧化钠、浓硫酸、硫酸亚铁,亚甲基蓝(上述试剂均为分析纯)。

1.2 试验方法

1.2.1 试验装置及操作方法

取一个长×宽×高=150 mm×150 mm×150 mm的玻璃容器,在其上方架上两条铜导线并固定住。分别裁剪一块10 cm×6.0 cm的多孔钛网电极板和不锈钢板分别作为阴、阳两极的电极,将其放入含有1 000 mL的50 mg·L-1亚甲基蓝染料模拟废水的电解槽中,调节极板间距和印染模拟废水溶液的初始pH值(用稀硫酸和稀氢氧化钠溶液调节),并投加1.0 g的无水硫酸钠,将电解槽置于恒温加热磁力搅拌器加热至试验所需温度25 ℃,然后往电解槽中投放试验所需量的硫酸亚铁颗粒(以每升印染模拟废水中投放的Fe2+摩尔浓度为计算)和过氧化氢溶液并搅拌,同时接通电源开始通电,每隔5 min在同一位置取上清液测其吸光度,以确定最佳反应条件。

1.2.2 单因素试验设计

取1 000 mL 50 mg·L-1的亚甲基蓝模拟废水于试验装置中并用稀酸或稀碱溶液调节其初始溶液pH值然后依次加入1.0 g硫酸钠和一定量的硫酸亚铁及过氧化氢,再调节两极板电流值,于25 ℃的水浴中通电,开始后每5 min取上清液测其吸光度。以降解率为指标,考察了通电时间、pH、亚铁离子和过氧化氢投放量、电流强度(I)5个因素对其降解率影响。各个因素的变化取值范围为: pH(2.0、2.5、3.0、3.5、4.0),I(50、100、150、200、250 mA),硫酸亚铁投加量(0.125、0.15、0.175、0.2、0.225 mmol),通电时间(5、10、15、20、25、30、35、40、45、50 min)。

1.2.3 响应面试验设计

在单因素试验基础上,以通电时间(A)、pH值(B)、电流强度(C)、硫酸亚铁投放量(D)、过氧化氢投放量(E)5个因素,利用Design-expert 10软件中的Box-Behnken中心拟合原理以降解率为响应值,进行五因素三水平响应面试验设计,试验设计编码表见表1。

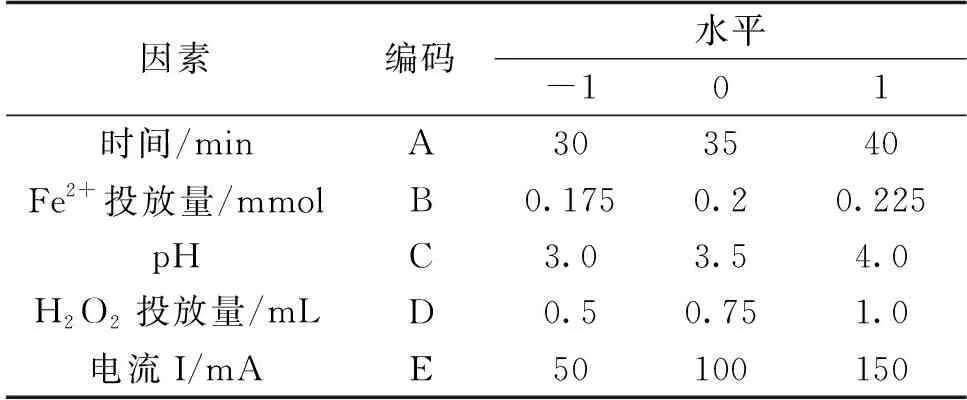
表1 设计因素与水平

1.2.4 废水降解率的计算

使用紫外分光光度计在664 nm分别测定溶液初始吸光度和降解后吸光度,然后计算亚甲基蓝模拟印染废水的降解率。

降解率的计算公式如下:

(1)

式中:A0——初始废水溶液吸光度值;

At——t时刻废水溶液的吸光度值;

Et——t时刻废水溶液的降解率。

2 结果与分析

2.1 单因素试验结果与分析

2.1.1 不同原始溶液pH对降解率的影响

取5组1 000 mL 50 mg·L-1的亚甲基蓝模拟废水分别加入5个试验装置中然后依次加入1.0 g硫酸钠电解质和0.175 mmol的硫酸亚铁、1.0 mL 30%过氧化氢溶液,调节其初始溶液的pH值分别为2.0、2.5、3.0、3.5、4.0再调节两极板电流值200 mA,于25 ℃的水浴中通电45 min,每5 min在同一位置吸取上清液并测其吸光度,考察不同亚甲基蓝模拟废水初始pH值对降解率的影响。试验结果如图1所示。

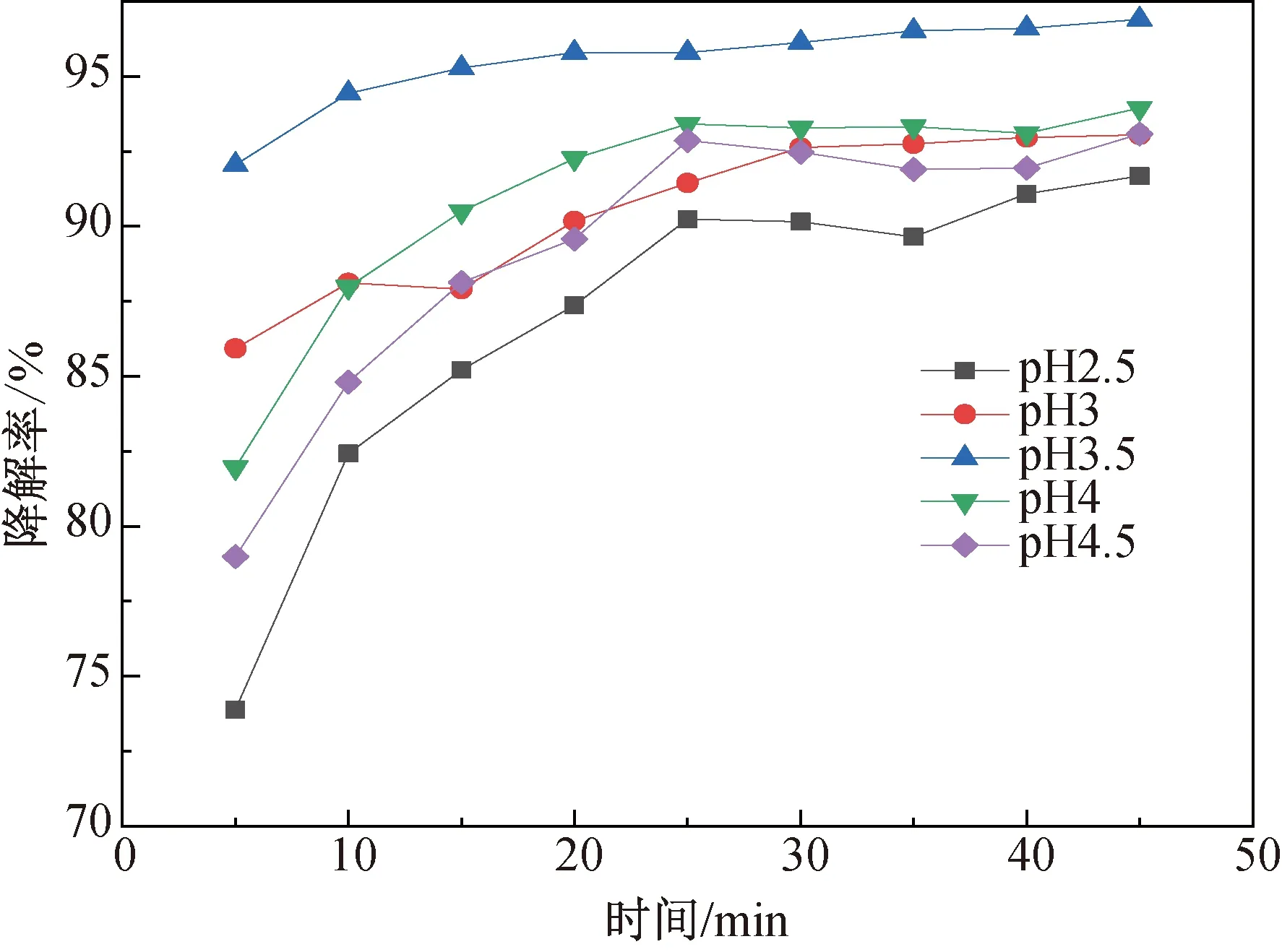
图1 pH对降解率的影响

由图1可知,当废水溶液初始溶液pH值在2.5～3.5之间变化时溶液的降解率随pH增大而升高,在pH 3.5～4.5之间时降解率随pH增加而降低,由于pH值过小时,在阴极表面发生析氢副反应[12],会影响Fe2+的催化再生以及HO2·的产生,降低了其对染料废水脱色降解能力[13]。当pH值过高时,不仅抑制·OH的产生,还会使亚铁离子和铁离子以氢氧化物的形式产生沉淀,导致脱色率降低[14-15]。在pH为3.5时降解率出现最高值。因此综合考虑确定该研究中亚甲基蓝模拟废水的初始最佳pH值为3.5。

2.1.2 不同电流大小对降解率的影响

按2.1.1方法固定其它因素条件,再分别调节两极板电流强度值I(50、100、150、200、250 mA),于25 ℃的水浴中通电45 min,每5 min在同一位置吸取上清液并测其吸光度,考察不同电流大小对亚甲基蓝模拟废水降解率的影响。试验结果如图2所示。

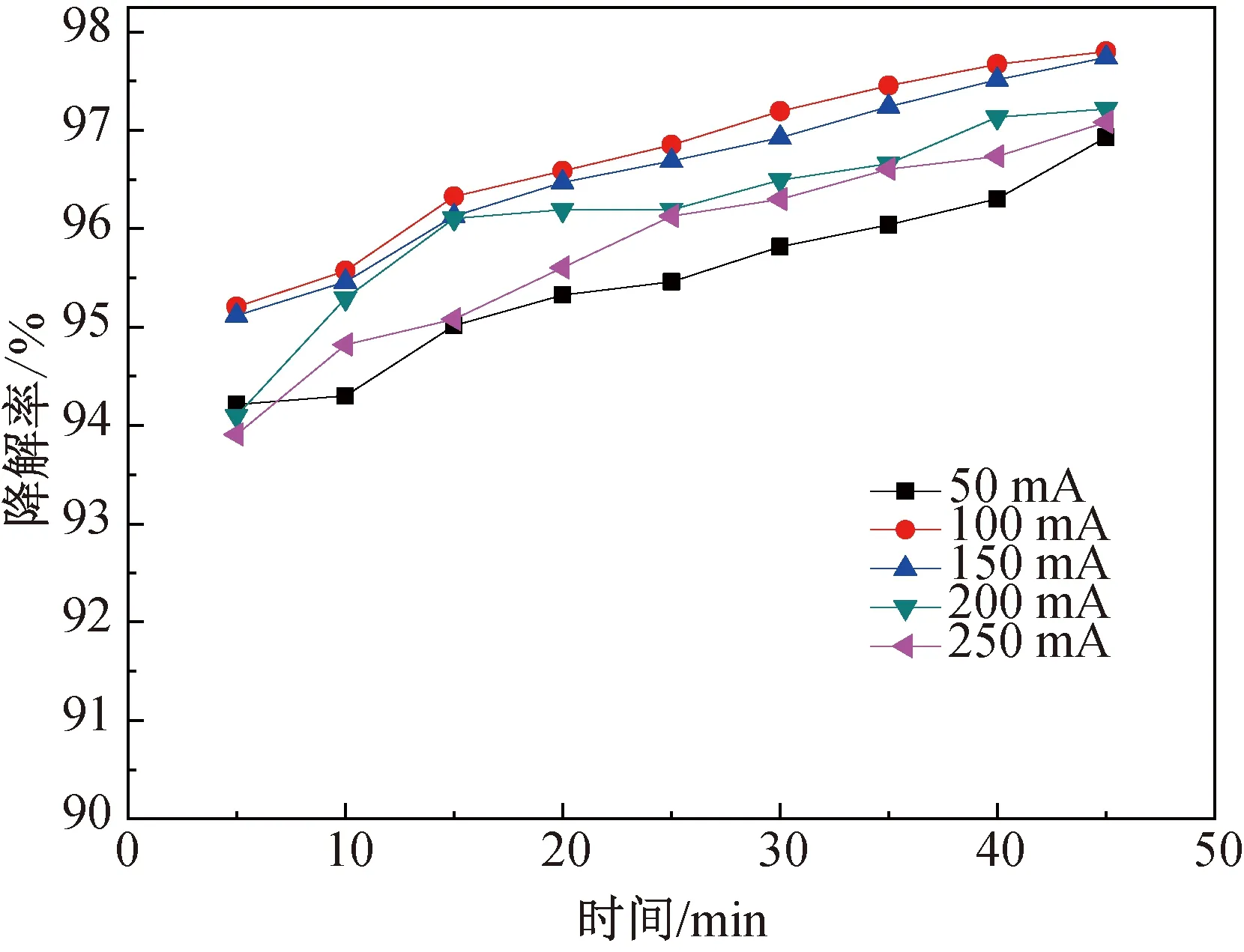
图2 电流对降解率的影响

由图2可知,电流(I)在50 mA～100 mA时降解率随电流强度增加而升高,当电流值在100 mA～250 mA变化时降解率随电流强度增高而降低。出现这种现象的原因是电流强度越大,单位时间内提供的电子越多,生成的H2O2越多[16],越有利于·OH的生成,从而使废水的降解率增大,当电流为100 mA时降解率增加到最值;但当电流过大时,H2O2会发生以下反应[17]:

O2+2H++2e-→H2O2

(2)

H2O2+2H++2e-→2H2O

(3)

因此,电流强度过大且pH比较低时反而消耗H2O2,而不利于·OH生成而使降解率有所降低。因此综合考虑确定电芬顿降解亚甲基蓝模拟废水的最佳电流强度为100 mA。

2.1.3 不同H2O2投放量对降解率的影响

按2.1.1方法固定其它因素条件,再分别加入0.5、0.75、1、1.25、1.5 mL 30%过氧化氢溶液于上述5组相同浓度的模拟废水溶液中,于25 ℃的水浴中通电45 min,每5 min在同一位置吸取上清液并测其吸光度,考察不同H2O2投放量对降解率的影响。试验结果如图3所示。

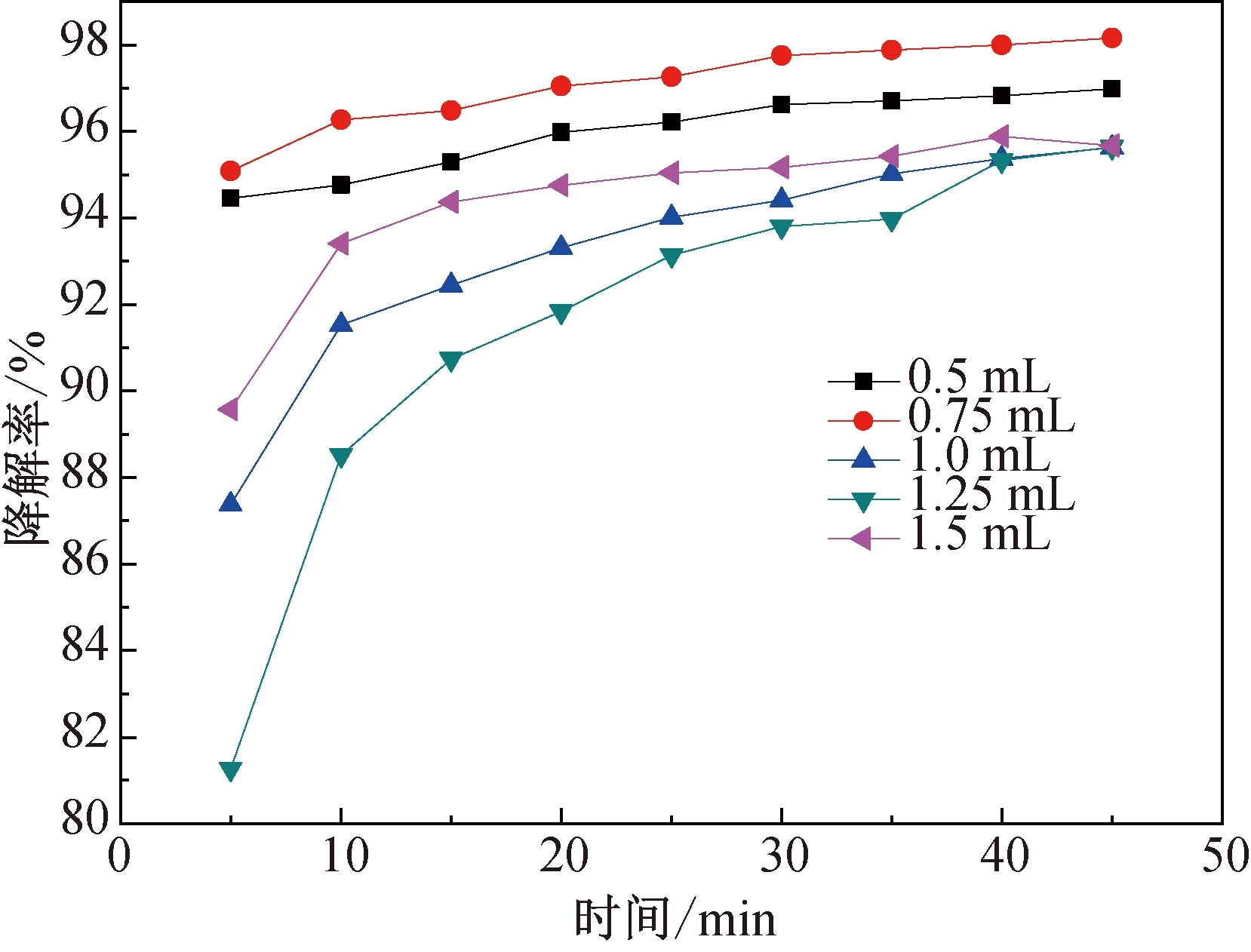
图3 H2O2投放量对降解率的影响

由图3可知,在H2O2投放量0.5 mL～0.75 mL时废水的降解率随着H2O2投加量的增加而增大,这是由于H2O2会与溶液中的Fe2+发生芬顿反应产生的羟基自由基能够促进废水的降解[18],因此降解率随着H2O2投加量的增加而升高;而在H2O2投加量在0.75 mL～1.5 mL时降解率随H2O2投放量增加而减少。综合考虑故选择H2O2投加量为0.75 mL。

2.1.4 不同Fe2+投放量对降解率的影响

按2.1.1方法固定其它因素条件,再分别投加0.125、0.15、0.175、0.2、0.225 mmol的FeSO4·7H2O于上述5组模拟废水溶液中,于25 ℃的水浴中通电45 min,每5 min在同一位置吸取上清液并测其吸光度,考察不同亚铁投放量对降解率的影响,得到结果如图4所示。

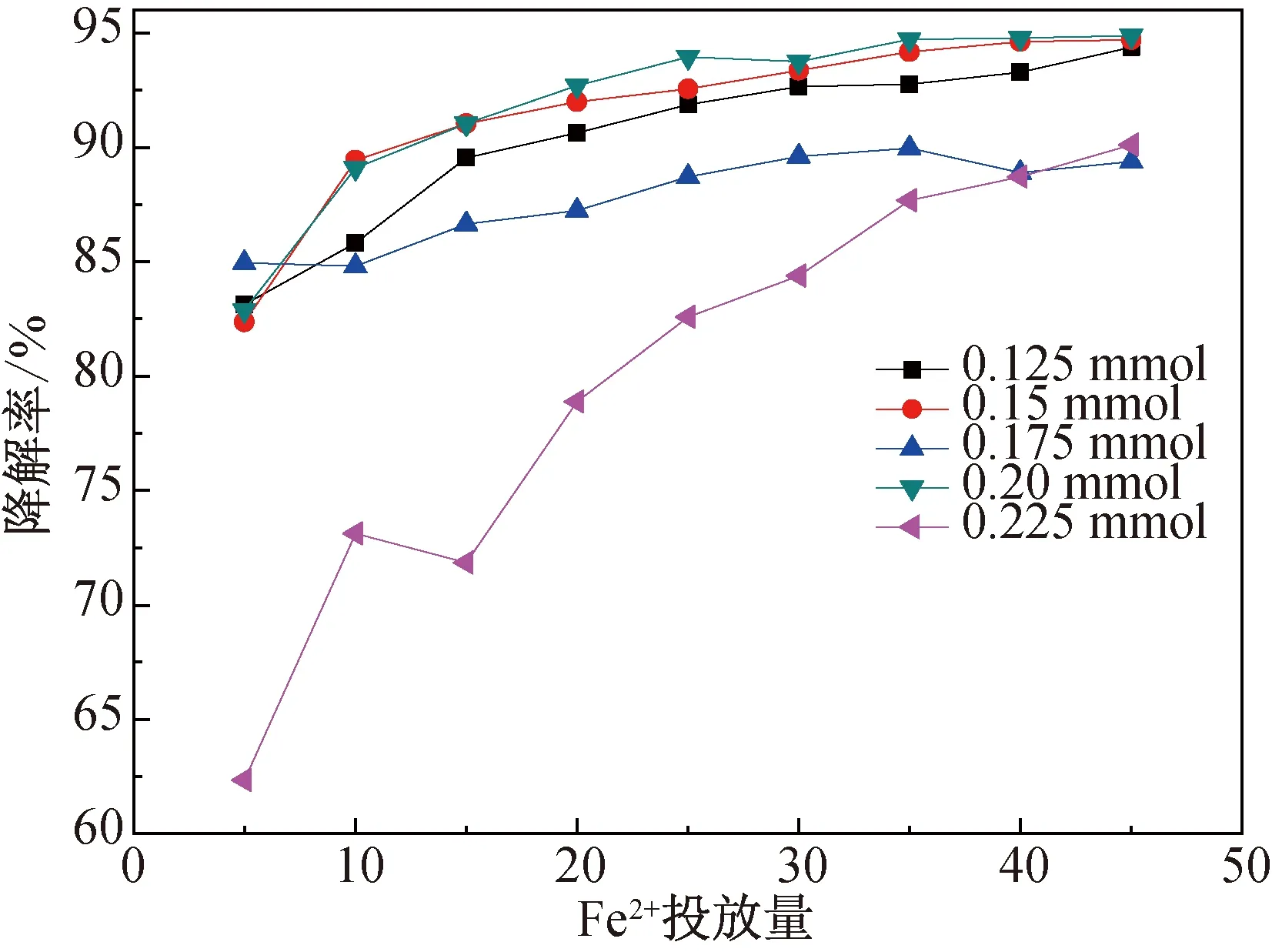
图4 亚铁投放量对降解率的影响

由图4可知,当Fe2+初始投加量在0.125 mmol～0.2 mmol之间时,降解率随着Fe2+初始浓度的升高而升高,在Fe2+初始投加量为0.2 mmol时降解率达到最大值;随Fe2+投加量继续增加至0.225 mmol时降解率开始下降。这可能原因可以从电芬顿反应机理的基本反应式(4)可知:在适当的Fe2+的浓度范围内随Fe2+升高有利于·OH的产生从而使降解率逐渐增大;但随Fe2+投加量的继续增加时,从电芬顿反应机理的基本反应式(5)可得知,过量的Fe2+会与·OH发生副反应而消耗掉溶液中的·OH,不利于降解率的提高,过量的Fe2+被氧化成Fe3+[19],所以会出现使降解率下降的情况。

H2O2+ Fe2+→OH-+·OH+ Fe3+

(4)

·OH+Fe2+→Fe3++ OH-

(5)

综上所述,过高与过低的Fe2+初始浓度都不利于反应进行,因此综合考虑选择Fe2+初始投加量0.2 mmol。

2.1.5 不同通电时间对降解率影响

按2.1.1方法固定其它因素条件,考察通电时间为5、10、15、20、25、30、35、40、45、50 min时对降解率影响,得到结果如图5所示。

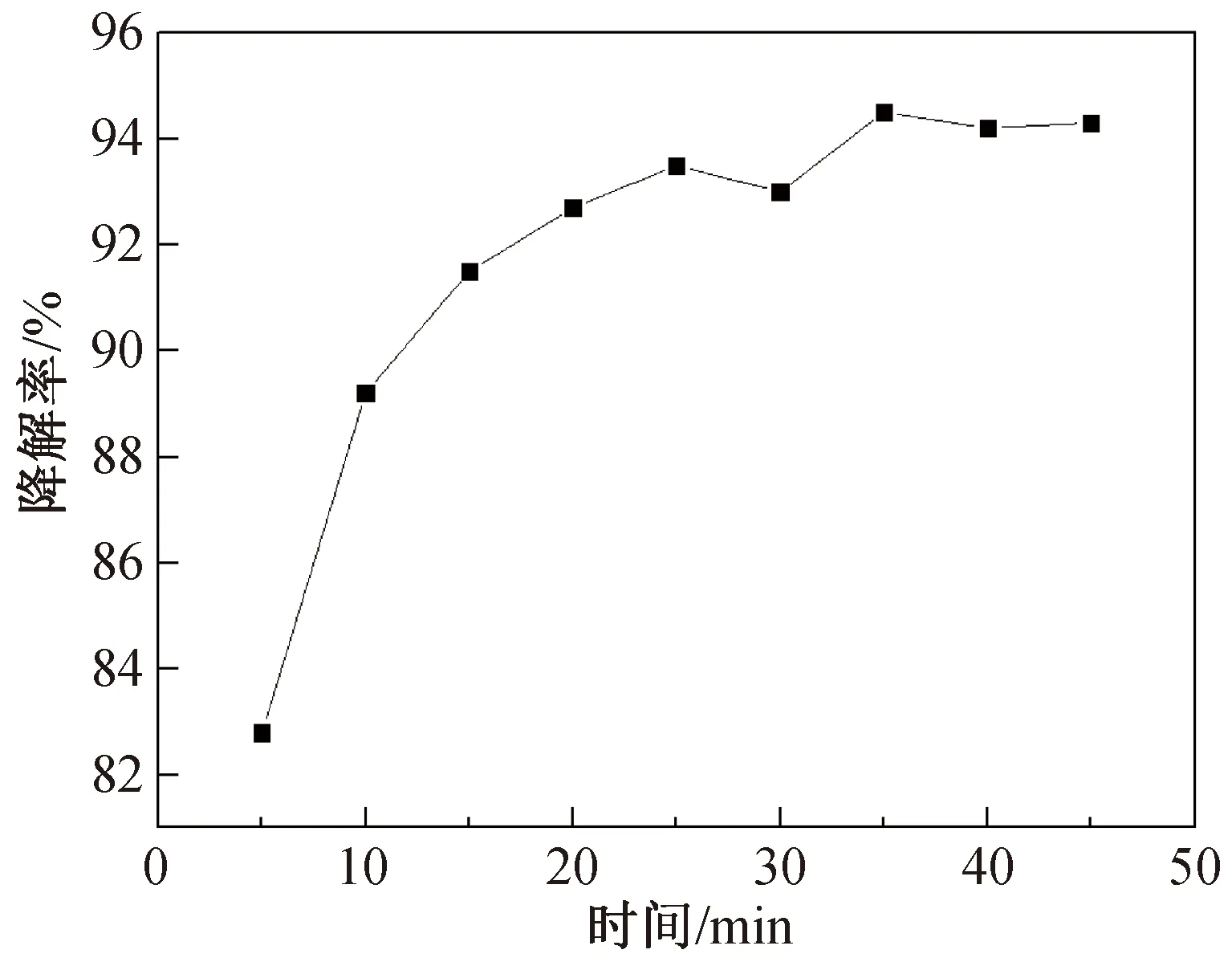
图5 时间对降解率的影响

由图5可知试验在35 min之前降解率随时间的增加而升高,35 min之后降解率趋于平稳。考虑到节约时间成本故选择35 min。

2.2 响应面试验设计结果及分析

2.2.1 响应面试验设计结果

试验以模拟废水降解率为指标,在单因素试验的基础上以通电时间、亚铁投放量、pH、过氧化氢投放量、电流强度为影响因素,设计了5因素3水平共46个点的试验方案,试验结果如表2所示。

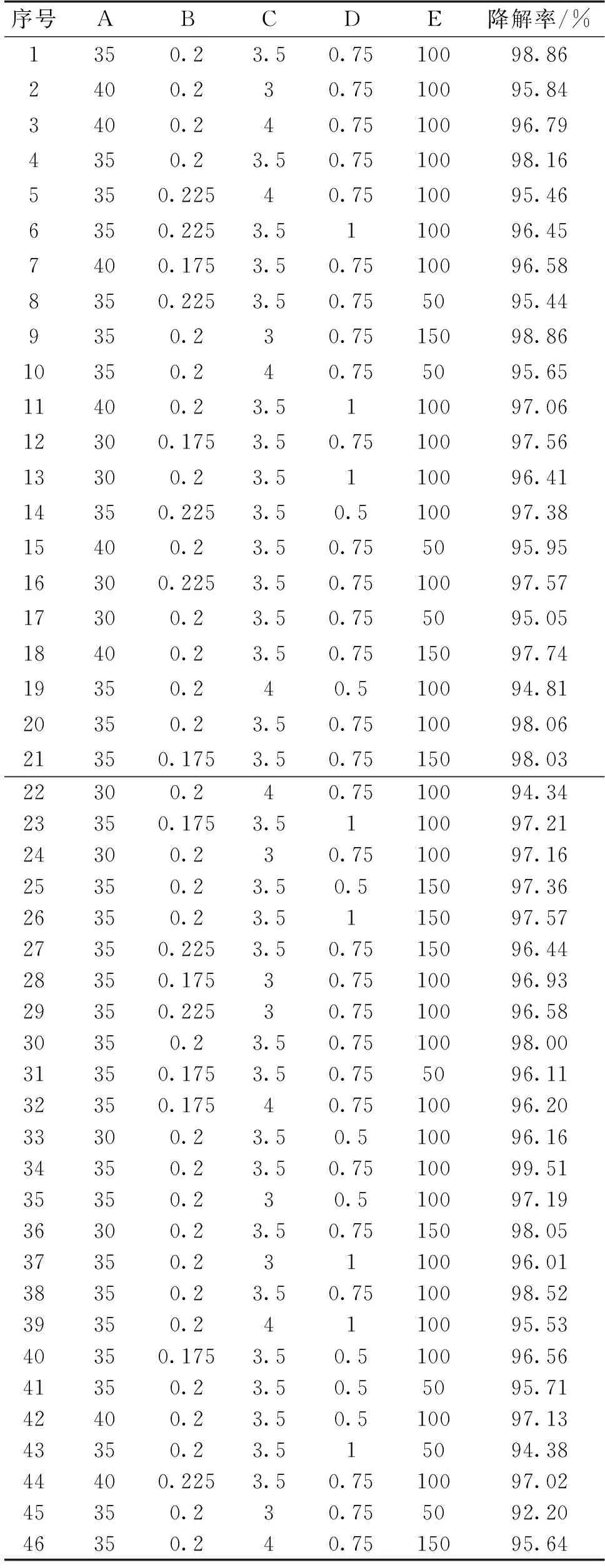
表2 试验结果

2.2.2 回归模型建立及方差分析

对电芬顿法降解印染模拟废水(亚甲基蓝)的降解率数据结果进行模型建立和方差分析结果见表3。

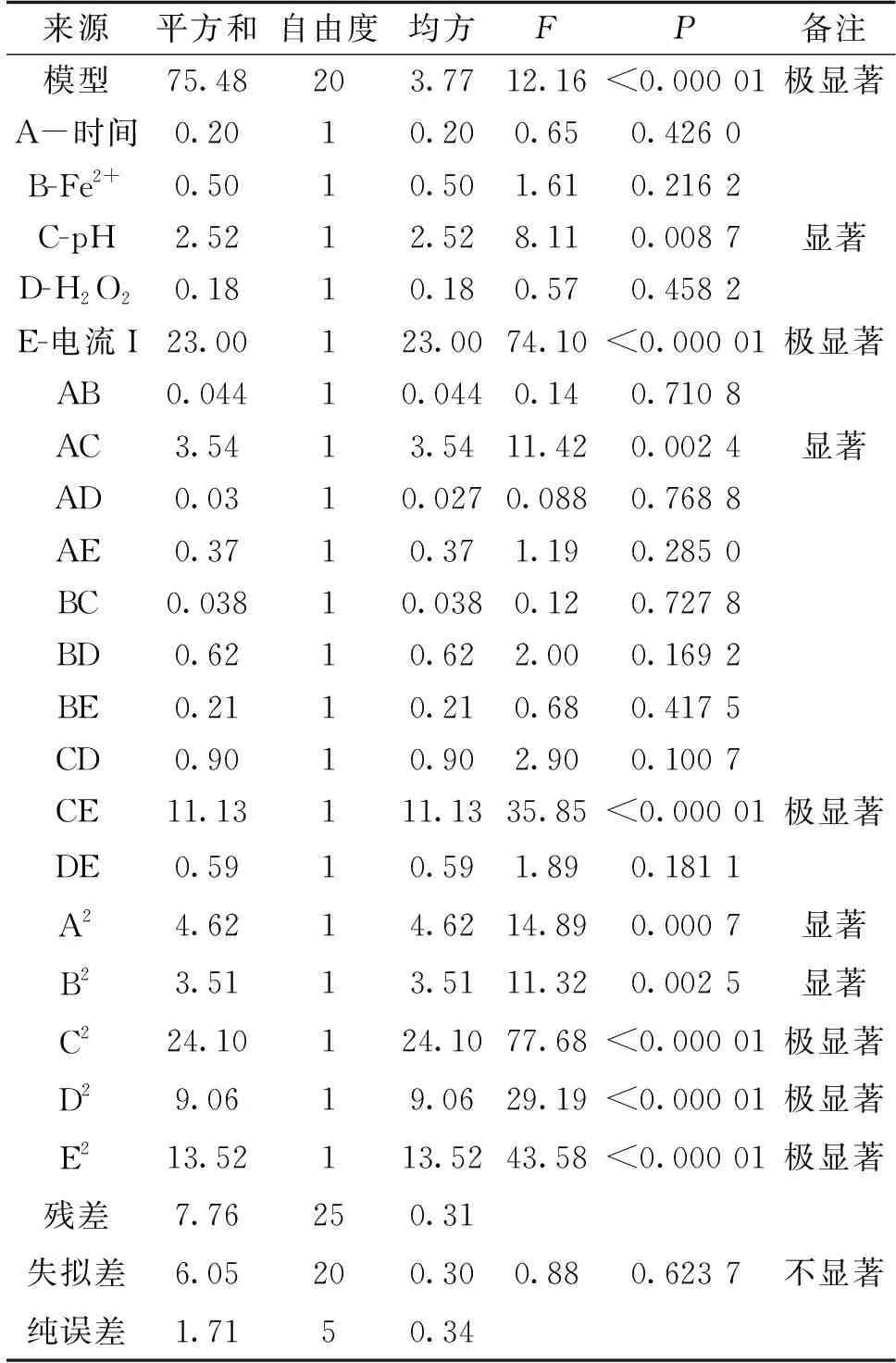
表3 二次多项式回归方程的方差分析

由响应面软件对试验结果进行数据分析得出模型回归方程为:

Y=98.52+0.11A-0.18B-0.40C-0.10D+1.2E+0.10AB+0.94AC-0.083AD-0.30AE-0.098BC-0.39BD-0.23BE+0.47CD-1.67CE+0.38DE-0.73A2-0.63B2-1.66C2-1.02D2-1.24E2

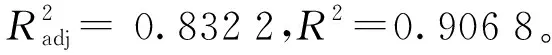
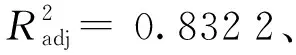
2.3 响应面各因素间的交互关系

图6为各个因素交互关系响应面图,由图可以直观地看出各响应面最大值所对应的因素水平,也可以由响应曲面的曲率反映各因素交互作用的强弱,曲率越大因素交互影响越大[20]。如图所有曲面都为凸型面,即所选范围响应值存在最大值(同时从回归方程的二次项系数都为负数说明响应面图形开口向下亦可说明其存在最大值)。在本试验中,每个响应面曲面图均为固定另3个因素后对其它2个因素进行分析,图6表现出两因素之间的交互作用,各个曲面图图形边缘线的陡峭和平缓均直接地反映了各因素对降解率的影响,如图6i图形边缘陡峭程度可知对降解率的影响电流强度(I)大于pH,同理分析图6a、6e、6h可获知对降解率的影响关系分别为:pH>亚铁投放量、亚铁投放量>时间、时间>H2O2这与表3显示的结果是一致的。

2.4 验证试验

根据响应面实验结果得到本试验的最佳工艺条件为:通电时间31.634 min,Fe2+投放量0.192 mmol,pH=3.102,H2O2投放量0.760 mL,电流强度150 mA的条件下,预测降解率为98.4%。考虑到实验的可操作性,将最佳工艺条件调整为:通电时间32 min,Fe2+投放量0.19 mmol,pH=3.1,H2O2投放量0.760 mL。

为验证模型的可靠性,在调整后的最有工艺条件下进行3组平行试验,得到平均降解率为97.3%,与预测的降解率98.4%相对偏差1.12%,小于5%。两者吻合度较高,说明模型能很好预测亚甲基蓝模拟废水的降解率,优化后的工艺参数条件是可靠的,能够为印染废水的处理提供技术参数。

3 结论

采用响应面法以降解率为评价指标对电芬顿法处理亚甲基蓝模拟废水的工艺条件进行优化,得出以下结论:

(1)由实验结果及响应面分析得出模型的回归方程为:

Y=98.52+0.11A-0.18B-0.40C-0.10D+1.2E+0.10AB+0.94AC-0.083AD-0.30AE-0.098BC-0.39BD-0.23BE+0.47CD-1.67CE+0.38DE-0.73A2-0.63B2-1.66C2-1.02D2-1.24E2;由回归方程的一次项系数模的大小得到各因素对降解率的影响顺序为:E(I,电流强度)>C(pH)>B(亚铁投放量)>A(时间)>D(H2O2投放量);由模型的回归效果显著、失拟项不显著以及相关系数可说明本次试验使用的染料废水处理工艺是可靠的。

(2)通过响应面试验结果及建立的回归模型的分析结果得到电芬顿降解亚甲基蓝印染废水的最佳工艺条件为:通电时间31.634 min,Fe2+投放量0.192 mmol,pH=3.102,H2O2投放量0.760 mL,电流强度150 mA的条件下,预测降解率为98.4%。

(3)利用模型得到了最佳工艺并且进行三组平行试验,得到了亚甲基蓝溶液平均降解率97.3%,而模型预测值为98.4%与平均降解率相对偏差为1.12%,说明模型能很好预测亚甲基蓝模拟废水的降解率,进一步说明了优化后的工艺参数条件是可靠的,能够为印染废水的处理提供技术参数。

(4)不足之处,文中还未对废水溶液温度、硫酸钠的添加量对亚甲基蓝模拟废水的降解率影响进行探讨,在后续的研究还需继续补充完善。