不同过冷度条件下HCP-Mg 凝固过程中的空位捕获
2023-06-11付佳豪张伯阳吴永全
付佳豪, 张伯阳, 张 开, 周 涛, 汪 昊, 吴永全
(上海大学材料科学与工程学院省部共建高品质特殊钢冶金与制备国家重点实验室, 上海 200444)
空位是材料中最至关重要的缺陷, 会严重影响诸如金属蠕变、屈服极限、半导体掺杂、光学器件吸收谱等重要材料属性[1-3]. 空位的形成通常是在材料加工的早期——凝固过程中被捕获进晶体. 这种捕获通常会造成其浓度超过平衡浓度, 称为“捕获效应”. Hillert 等[4]基于固液界面的渐变模型, 构建了一个用于描述纯金属快速凝固过程中空位捕获的经验模型, 并认为空位捕获必须在凝固速度超过1 m/s 的条件下才会发生.
空位捕获现象是公认的事实[5], 但关于凝固过程中空位捕获的微观机理研究明显不足. 目前相关分子动力学(molecular dynamics, MD)研究已是主流, 但在空位乃至缺陷捕获方面的研究相对较少, 对纯金属的研究则少之又少. Zheng 等[6]和Kramer 等[7]报道的空位捕获现象都是针对合金. Zhang 等[8]通过固液共存法研究了面心立方(face-centered cubic, FCC)金属空位捕获浓度随过冷度的变化, 是少有的针对纯金属空位捕获MD 研究的报道. 该研究发现空位浓度与凝固速度几乎呈线性增加, 这与Hillert 等[4]的模型描述有所不同. 显然, 凝固速度实际对应于过冷度, 但目前关于空位捕获浓度与过冷度之间的确切关系还尚未明确.
造成目前纯金属空位捕获微观机理研究不足的原因有二: 一是依靠单一技术实现由浅至深过冷度很难, 目前的物理实验还无法实现纯金属的最大深过冷度, 而传统MD 模拟技术只能实现深过冷度而无法触及中至浅过冷度[9]; 二是空位难以定位, 尤其是纯金属的空位, 这严重阻碍了空位的相关研究. 对于物理测量, 比如正电子湮灭或膨胀法[10-11], 因样品可能存在晶界, 很难精确获得材料中真实的空位浓度. 对于计算机实验, 空位因其原子尺度, 在材料中就像一个无形的“小鬼”, 在热振影响下很难被精确识别和定位, 也就无法获得凝固样品的空位描述[12-13].
为此, Wu 等创建了一种时间平均原子体积谱(time-averaged atomic volume spectrum,TAVS)方法(研究成果尚未公布), 用于精确标定空位, 尤其是体积最小的单空位. 该方法的基本逻辑如下: 虽然空位是不定型不定位的微小空间, 但原子是确切定位的实体, 如果能够精准定位包裹着空位的“原子笼”(atomic cage), 空位也就被精准定位. 通过该方法, 无论什么尺寸什么形状的空位, 都能够精准标定和定位. 而已有的HA 索引法[14-16]和最流行的Wigner-Seitz 法[12,16-26], 却只能分析瞬态构型而无法对抗热振噪音, 无法标定较小的空位,尤其是尺寸最小但数量占绝对优势的单空位.
基于TAVS 方法的技术支撑, 本工作研究了不同过冷度的密排六方(hexagonal closepacked, HCP)金属Mg 凝固过程中的空位捕获. 首先, 通过3 种不同的MD 技术, 分别实现了浅、中、深3 种过冷度. 然后, 通过TAVS 方法对3 种过冷度实验及退火后的样品进行了缺陷标定和分析. 最后, 获得了3 种过冷度条件下的空位浓度和分布, 同时也通过退火进一步观察了被捕获空位的消失.
1 实 验
本工作采用LAMMPS 软件对Mg 进行了不同过冷度凝固的MD 模拟, 结果如图1 所示.筛选了Sun 等[27]开发的嵌入原子势来描述原子间的相互作用. 所有的模拟都设置三维周期性边界条件, 方程积分采用蛙跳法[28]. 采用Noose-Hoover 恒温器和Andersen 恒压器[29]控制温度和压力, 压力设置为100 kPa, 所有的模拟积分步长设定为2 fs. 对原子的标定, 采用键取向序(bond orientation order, BOO)[30]和Voronoi 多面体指数(Voronoi polyhedron index,VPI)[31]相结合的方法, 用以区分各类不同原子. Li 等[32]已证实了该方法的有效性, 其中至关重要的是用到了Voronoi 空间分割原理, 因此本工作所涉及的原子体积均为Voronoi 体积.

图1 不同过冷度凝固下, 体系单位原子势能随时间的变化Fig.1 Potential energy of each atom varies with time under different undercooling degrees
采用国际上最经典的自然形核法(spontaneous nucleation)[33]来实现深过冷度的凝固. 首先,构建一个初始单晶(尺寸为33×19×40,共计100 320 个原子),在等温等压(normal pressure and temperature, NPT)系综下进行模拟. 然后, 将其直接升温至1 300 K(势函数对应的理论熔点为922 K[27])完全熔化, 再以5×1010K/s 的速度降温, 体系在大约630 K 发生结晶(见图1(a), 势能曲线在630 K 发生突变), 此时对应的过冷度为∆T=922—630=292 K, 相对过冷度约1/3, 属于最大深过冷度. 由于深过冷度的随机形核, 本工作进行了多次模拟, 并发现其随机性表现为空位浓度在某一个平衡值波动. 因此, 本工作选取了一个最具代表性的样本作为深过冷度样本.
采用诱导凝固法(embedded-seed induced crystallization)[34]来实现中过冷度的凝固, 即在液相中手动嵌入一个固相纳米球(见图1(b))以诱导体系凝固, 该模拟在NPT 系综下进行.首先, 构建一个初始单晶(尺寸为32×20×39, 共计99 840 个原子), 嵌入固相纳米球(2 nm 半径, 4 000 个固相原子). 然后, 直接模拟从已有晶核开始结晶的过程, 省略了冗长的形核过程.纳米球尺寸决定了能够发生凝固的临界温度(830∼840 K). 在该温度以下(本工作选择820 K),纳米球都可以诱导体系凝固, 对应的过冷度为∆T=922—820=102 K, 属于中过冷度.
采用固液共存法(solid-liquid coexisting method)[35]来实现浅过冷度的凝固, 这是目前唯一的方法. 首先, 通过NPT 和等压等焓(normal pressure and enthalpy, NPH)系综完成固液共存体系的构建(见图1(c), 体系的初始尺寸为20×15×82, 共计98 400 个原子, 通过调节总能量让体系固液比达到1∶4.5)[36]. 然后, 将体系放入NPT 系综进行弛豫, 弛豫温度为900 K(压力为101.325 kPa). 固液界面向液相移动发生凝固, 大约在3.2 ns 凝固结束. 对应的凝固速度为∼5.47 m/s, 过冷度为∆T=922—900=22 K, 属于浅过冷度.
3 种过冷度的凝固样本最终均降温到300 K 进行空位分析. 之后, 对3 个样本进行一致的退火处理, 即升温到900 K 保温4 ns, 再以5×1010K/s 的速度降温至300 K, 再次进行空位分析. 最后对3 个过冷度下的凝固样本及其退火样本进行了分析.
2 标准谱的建立
在进行空位捕获实验之前,需要建立HCP理想单晶典型空位的标准原子体积谱,以供后续参照. 本工作建立了一个拥有完美轴的HCP晶体, 原子总数为480.与FCC 晶体不同, HCP 晶体的密排面只有一个(0001)面, 这使得多空位具有多样性.
本工作构建了1 种单空位(monovacancy)、2 种双空位(divacancy)和3 种三空位(trivacancy). 2 种双空位的区别在于2 个相邻的空位位(vacancy site)是否在同一密排面.3 种三空位中有2 种的3 个空位位在同一密排面, 且两种情况由上下两层的堆垛方式决定: 一种是ABAB 型; 另一种是ACAC 型; 第3 种是有一个空位位不在同一密排面. 这些空位都是通过手动删除对应位置的原子形成的.
产生人工空位后, 本工作对构型进行了Voronoi 分析, 给每个原子赋予Voronoi 体积. 于是部分原子因为空位的相邻而发生变化, 形成了除正常原子(normal atom, NA)以外的多种空位原子(vacancy atom, VA). 这些VA 因为毗邻于空位位而获得了多余的体积(redundant volume), 使得它们的体积大于NA. 基于此, 本工作定义了原子归一化体积, 即
本工作所构建的6 个典型空位如图2 所示, 其中最大的透明灰色球表示空位位, 白色球表示NA, 绿色球表示VAI, 蓝色球表示6 种VAII, 红色球表示2 种VAIII. 在标准体积谱中, 各种原子分别对应各自的特征峰. 与FCC 晶格中空位的标准结构相似, 图2 所示的HCP 单空位是被12 个VA 包裹形成的一个VA 笼, 双空位是被18 个VA 包裹形成的一个VA 笼; 但与FCC 的标准三空位不同, HCP的3 种三空位分别被21、23、24 个VA 包裹.

图2 6 个典型空位(单空位、双空位、三空位)和其在HCP 晶格中的VA, 以及它们的标准体积谱Fig.2 Six typical vacancies (monovacancy, divacancy, trivacancy) with VAs in the HCP lattice, and their standard volume spectra
图2 所示的体积谱显示了4 类峰, 分别对应4 种原子, 即NA、VAI、VAII和VAIII, 其中VAI、VAII、VAIII是分别毗邻1、2、3 个空位位的VA, 都具有不同的标准体积. NA的体积为1, VAI的体积为1.083 5, VAII有1.194 4、1.208 6、1.222 4、1.229 2、1.236 1、1.243 共6 种体积: VAIII有1.417、1.423 6 共2 种体积. 与FCC 晶体不同, HCP 的VAII和VAIII存在不同的精细分类, 主要是因为HCP 只有一个密排面.
3 结果分析
3.1 不同过冷度凝固过程的空位捕获
图3 为深过冷度凝固及退火样本的体积谱及最终构型. 相比图2 的标准体积谱图, 图3 的谱图具有很大的展宽且连续. 如图3(a)中的插图(局部放大图) 所示, 第一主峰NA 峰出现分峰. 这是因为极快的凝固速率形成了两个晶粒(见图3(d)中的浅蓝和深蓝两块区域). 由于深过冷度体积谱图的空位峰是连续的, 无法对VA 进行精细分类, 因此统一用红色表示所有VA.首先, 空位结构图中的所有VA 都是以完整的VA 笼结构出现(后续中过冷度和浅过冷度的空位构型亦如此). 这些VA 笼存在固定的VA 数, 例如12 个VA 笼对应单空位, 18 个VA 笼对应双空位, 依此类推, 与图2 的标准结构图完全吻合. 与此同时, 还存在一些超出标准结构图的大VA 数的VA 笼. 这些VA 笼对应大尺寸空位, 其中一个最大尺寸空位是38 倍空位, 对应的VA 笼有88 个VA. 此时, 甚至可以称其为空腔(cavity). 在相同的凝固速度下, 相对于FCCAl, HCP-Mg 凝固过程捕获的空位更大, 使得体积谱中的最大VA 达到3.627 7, 而FCC-Al 中的最大VA 则小于2.7.

图3 深过冷度凝固样本和其退火样本的8 ps 平均体积谱, 以及最终的空位结构图和晶体构型图Fig.3 8 ps-averaging volume spectra of deep undercooling solidified sample and its annealed sample, as well as the final vacancy configurations and crystalline configurations
基于此, 本工作分析统计了所有捕获空位的尺寸和数量, 如表1 所示. 对于图3(b) 中退火样本的体积谱(插图为局部放大图), NA 峰依旧存在分峰, 意味着两颗晶粒未融合. 这与FCC-Al 经过相同退火经历完全融合成一个单晶粒的现象不同. 此外, HCP-Mg 退火后的空位大幅减少, 而FCC-Al 退火后的空位浓度变化不大. 与FCC-Al 相同的是, HCP-Mg 经过退火,所有的大空位全部消失, 剩下的少量空位均为单空位.

表1 3 种过冷度凝固及其退火样本中不同尺寸空位对应的数量Table 1 Numbers of different kinds of vacancies in solidified and annealed samples under 3 types of undercooling degrees
图4 所示为中过冷度凝固样本和其退火样本的体积谱及空位结构图. 因为中过冷度样本依附唯一晶核长大, 所以体系结晶成单一晶体(后续浅过冷度亦如此). 对应地,图4 中的NA 峰没有分峰, 但VA 峰开始出现明显分峰, 可据此对其进行精细划分, 即VAI峰(∼1.094 2)、VAII峰(1.21∼1.33)、VAIII峰(1.42∼1.63)以及唯一一个VAIV峰(∼1.75).

图4 中过冷度凝固样本和其退火样本的8 ps 平均体积谱, 以及最终的空位结构图Fig.4 8 ps-averaging volume spectra of medium undercooling solidified sample and its annealed sample, as well as the final vacancy configurations
单空位峰在1.094 2 附近, 大于图2 中的标准峰(1.083 5), 这又一次与FCC 情况相反. FCC 的VAI峰在1.07 附近, 即VA 存在内缩移动(inward displacement), 但HCP 的VA原子却是外扩移动(outward displacement). 不仅如此, 相对于图2 中的标准谱图, 图4 中的VAII和VAIII峰都存在明显蓝移, 意味着与VAI峰同步的外扩移动.
与图3(c)相比, 中过冷度的空位数量显著降低, 且空位尺寸也显著减小, 基本以单空位到三空位为主, 没有超大的空腔型空位. 退火样本的两个VA 峰分别为VAI峰和VAII峰, 此时VAIII峰和VAIV峰消失, 多倍空位也全部消失, 整个体系只存在单空位与双空位, 但数量相较于退火前不降反升. 这说明退火不仅使多倍空位分解为更小的空位, 同时也使一部分空位消失. 与深过冷度相比, 中过冷度退火造成的空位消失明显减少, 甚至中过冷度退火样本的空位浓度数倍于深过冷度.
图5 所示为浅过冷度凝固样本和其退火样本的体积谱及空位结构图. 与图3 和4 相比, 浅过冷度样本中的VA 峰只存在一个简单的VAI峰, 并且该峰与NA 峰已经严格分离. 这意味着浅过冷度捕获的所有空位都是单空位. 不仅如此, 这些单空位都是分散存在, 没有出现相邻形式, 原因是没有出现链接VAI(adjacent VAI), 而这也是与FCC-Al 的不同之处.

图5 浅过冷度样本和其退火样本的8 ps 平均体积谱, 以及最终的空位结构图Fig.5 8 ps-averaging volume spectra of shallow undercooling solidified sample and its annealed sample, as well as the final vacancy configurations
本工作采用的浅过冷度温度(900 K)几乎接近于熔点(922 K), 使得体系的凝固速度已接近于Hillert 模型[4]预报的无捕获效应的极限速度, 因而最终捕获的空位浓度也接近于该温度的平衡浓度. 研究发现, 退火后整个体系的空位几乎完全消失, 只剩下1 个单空位, 显著低于退火温度对应的平衡浓度. 该现象更甚于FCC-Cu 在辐射后空位的退火消失程度.
以上3 种过冷度获得的空位尺寸及其数量如表1 所示. 对比表1 的数值, 图3∼5 中的空位结构图给出的定性结论更加清晰明确. 仅从凝固样本空位位的数量来看, 空位捕获的数量存在“深过冷度>中过冷度>浅过冷度”的规律. 不仅如此, 随着过冷度由深至浅, 所捕获空位的尺寸也越来越小. 与FCC 的规律一致, 无论什么过冷度, 单空位数量永远占绝对优势. 在经过退火处理后, 深过冷度的空位消失率远高于中过冷度和浅过冷度, 即空位消失率也存在“深过冷度>中过冷度>浅过冷度”的定性规律. 退火后, 深过冷度的空位浓度已接近900 K 的平衡浓度,中过冷度却仍远高于平衡浓度, 而浅过冷度则接近于全部空位消失.
3.2 冗余体积与空位浓度
根据FCC 金属以及从头算空位形成体积(formation volume)[22]的普遍规律, VA 笼的冗余体积均小于1, 即空位周围的VA 在热振条件下的平衡位置向空位中心移动, 这就是所谓的“内缩移动”. 按照定义, 理想单空位VA 笼的冗余体积应为1(见图2(a)所示的标准单空位,其VA 笼冗余体积为0.083 5×12≈1). 然而, 根据图3∼5 的体积谱可知: 所有VA 均存在外扩移动, VAI峰都在1.093∼1.094 之间, 对应的冗余体积均大于1. 这与FCC 的内缩移动[22]规律完全相反.
为进一步确认此现象, 本工作分析了3 种过冷度凝固样本的单空位VA 笼的冗余体积∆Vcage. 同时分析了VA 笼及其第一近邻NA 壳层(NA shell)的总冗余体∆Vcage+shell, 结果如图6 所示, 其中横坐标为单空位的序列号. 由图6 可知, 中过冷度和浅过冷度的∆Vcage和∆Vcage+shell波动非常小, 而深过冷度的波动比较剧烈. 这是因为中过冷度和浅过冷度最终形成单一晶粒, 而深过冷度则存在两个晶粒, 且这两个晶粒的NA 体积存在明显区别(见图3 中NA 峰的分峰), 因而对应不同的标准体积实际上, 归一化过程采用的是两个标准体积的平均值, 因而造成了深过冷度冗余体积的剧烈波动, 但即便如此, 其值也始终围绕某个平均值波动(中过冷度和浅过冷度亦如此).

图6 单空位VA 笼和VA 笼+第一近邻NA 壳层的冗余体积分布Fig.6 Redundant volume distributions of all monovacancies VA cages, and all monovacancies VA cage + NA shell
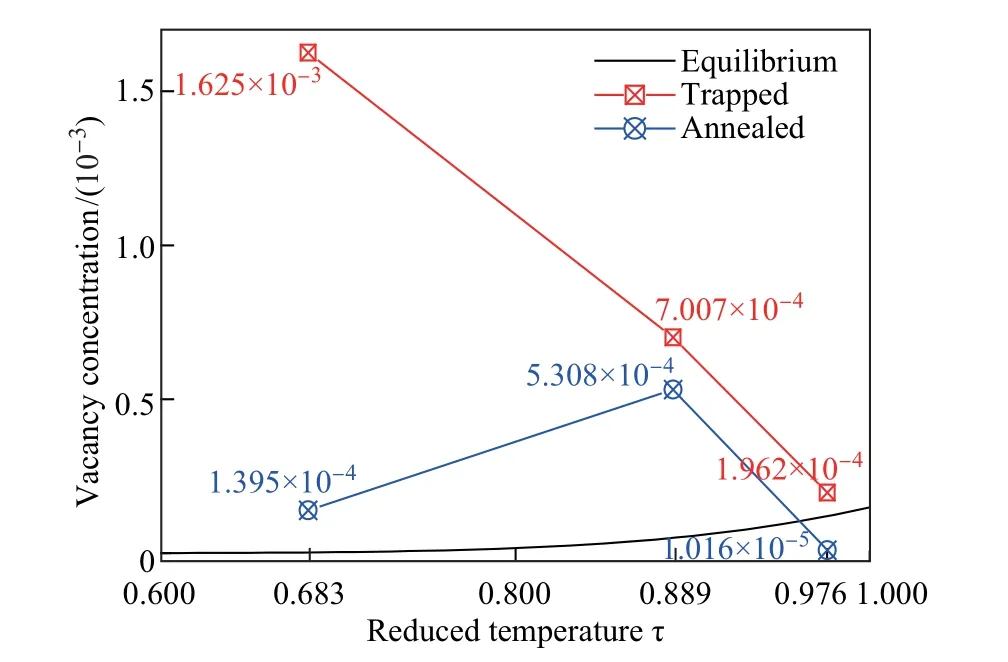
表2 所示为所求得的3 种过冷度的单空位平均冗余体积. 可见: ∆Vcage基本维持在1.11∼1.12 之间, 即超出标准体积1 约0.11 左右, 说明外扩移动是普适现象;cage+shell基本维持在1 附近.cage+shell 表2 单空位VA 笼和VA 笼+第一近邻NA 壳层的平均冗余体积Table 2 Averaged redundant volumes of all monovacancies VA cages, and all monova- cancies VA cage + NA shell 本工作按照空位位数量统计了凝固过程空位捕获浓度及其退火样本的空位浓度, 即 式中: nsite为空位位数量; Natom为原子数. 根据HCP-Mg 的空位形成焓和形成熵实验数据[37], 计算热力学平衡空位浓度曲线, 即 式中: τ = T/Tm为约化温度, 取值范围为0∼1, 其中τ = 0 对应0 K, τ = 1 对应熔点;为形成焓项;为形成熵项;Tm=922K;∆ef=0.7eV;∆sf=0 kB. 图7 所示为通过不同过冷度凝固捕获的空位浓度与热力学平衡空位浓度的比较.平衡空位浓度在热力学上是温度的函数(见图7 中的黑色曲线), 随温度的上升而增加, 且最高平衡空位浓度(对应于熔点, 即τ = 1)约为1.492×10−4. 凝固过程中捕获的空位浓度与平衡空位浓度正好相反, 随着温度的降低而显著增加, 且远高于平衡空位浓度. 这就是所谓的捕获效应(trapping effect). 这种规律与Hillert 等[4]的模型描述相符, 与Zhang 等[8]采用固液共存法获得的FCC 金属的情况也基本相符. 深过冷度凝固捕获的空位浓度甚至高达10−3数量级, 高出对应的平衡空位浓度3 个数量级. 浅过冷度凝固捕获的空位浓度非常接近平衡浓度, 即浅过冷度凝固的捕获效应接近0. 由此可见, 捕获效应规律非常明显: 随过冷度增大, 捕获效应显著增加; 反之, 随过冷度降低, 捕获效应也相应降低. 但是否存在当过冷度降为0, 捕获效应也降低为0 的同趋规律, 本工作的研究结果显示该规律基本成立, 后续仍需更系统深入的实验验证和理论解释来确定其普适性. 图7 平衡空位浓度与不同过冷度凝固捕获的空位浓度及其退火空位浓度Fig.7 Comparisons of equilibrium vacancy concentration with trapped concentrations of different solidification and concentrations after annealing 此外, 退火后的空位浓度也揭示了另外一些规律. 对表1 中的具体数值进行分析后发现:深过冷度捕获浓度最高, 但其退火后的空位浓度显著降低; 中过冷度的空位浓度在退火后减少不多. 分析原因认为: 深过冷度产生的其他大缺陷(如晶界、位错等)在退火过程中显著中和了空位缺陷, 这种现象在FCC-Al 中也同样存在; 中过冷度体系是单一晶粒, 除空位外应该只有自间隙原子(self-interstitial atom)的点缺陷存在(这些点缺陷在图3∼5 中NA 峰左边的长尾巴就有所表明). 正因如此, 中过冷度体系能够提供的间隙原子比较有限, 因而最终能够中和的空位也有限. 与中过冷度类似, 浅过冷度最终形成的也是单一晶粒, 因而除空位以外也只存在自间隙原子. 但特别的是, 浅过冷度的空位基本完全消失, 最终只剩1 个单空位, 远低于其平衡空位数(∼12). 仔细观察图5(c)可以发现, NA 峰的左边仍然存在体积较小的原子, 这些都是自间隙原子的体现. 由此判断, 无论是何种过冷度, HCP-Mg 凝固过程都会形成一定量的自间隙原子, 而它们是造成退火后空位消失的主要原因. 这一点与FCC 金属显著不同. FCC-Al 的凝固过程未发现任何自间隙原子, 只在FCC-Cu 高能辐射这种局部超快熔化凝固过程中才会出现少量自间隙原子. 本工作通过3 种MD 技术实现了HCP-Mg 的深、中、浅3 种过冷度凝固的空位捕获模拟实验. 据此, 采用TAVS 方法对空位进行标定, 研究了3 种过冷度下的空位捕获及其退火后的空位消失情况, 得到如下4 条结论. (1) HCP-Mg 凝固过程中的空位捕获效应非常明显: 随过冷度的增加, 捕获空位的浓度显著上升, 且远高于对应的平衡空位浓度. (2) HCP-Mg 凝固过程中也存在大量的自间隙原子捕获. 正因如此, 在中过冷度和浅过冷度退火后, 存在空位消失现象. 这应该是自间隙原子与空位的中和效果, 而这种中和效果甚至使浅过冷度退火后的空位几乎完全消失. (3) 相对于对称性更好的FCC-Al, HCP-Mg 更容易捕获超大空位, 比如空腔型空位. (4) 与FCC-Al 空位显著不同, HCP-Mg 的空位VA 笼存在外扩位移, 而不是普遍公认的内缩位移. 此外, 根据“随过冷度的减小, 捕获效应也减小”的捕获效应规律, 是否存在当过冷度降低为0, 捕获效应也降低为0 的同趋规律, 尚需后续进行更为系统深入的实验验证和理论解释.
4 结束语
