基于图论的并行计算技术教学内容模块化优化研究

吴建平　汪祥　杨锦辉　银福康　彭军

摘  要：并行计算技术课程是在大气海洋环境数值模拟对大规模科学与工程计算的需求越来越大的背景下开设的，但自开设以来，还存在教学内容过多、各知识点之间逻辑关系不十分清晰与讲授顺序不太合理等问题。该文基于对教学内容先按知识点进行划分，再基于教学目标牵引，利用图论技术进行知识点间依赖关系分析的方法，对教学内容进行精简与模块重新组织，以改进教学内容的针对性与知识点间的顺畅性，提升教学质量与学生学习效果。

关键词：并行计算；教学内容；模块化；依赖关系；图论

中图分类号：G642        文献标志码：A          文章编号：2096-000X（2023）17-0095-04

Abstract： The course of Parallel Computing Technology is set up under the background of the increasing demand for large-scale scientific and engineering calculation by numerical simulation of atmospheric and marine environment. However， since its establishment， there are still many problems， such as too many teaching contents， unclear logical relationship between knowledge points and unreasonable teaching sequence. Based on the division of teaching contents according to knowledge points， and then based on the direction of teaching objectives， the graph theory technology is used to analyze the dependence between knowledge points. The teaching content is simplified and reorganized to improve the focalization of teaching content and the rationality of the order of knowledge points， and to improve the teaching quality and students' learning effect.

Keywords： Parallel Computing; course content; modularization; dependency; Graph theory

大气海洋环境数值模拟是采用偏微分方程组对大气海洋状态演变规律进行数学建模，并采用数值方法进行求解，从初始状态进行未来状态预测的一种客观与定量预测方法，已越来越成为天气预报与海洋环境预报的主流方法。该方法不仅涉及到状态在时间维度上的演变，而且涉及到方程组在三维空间中的离散，形成离散网格，并在众多网格点或网格中心上进行计算，导致计算量巨大问题，而业务数值预报又对实时性要求很高，因此，采用高性能计算机进行并行数值模拟成为必然选择。欧洲中期天气预报中心、美国国家环境预报中心、英国气象局、法国气象局、德国气象局、日本气象厅与加拿大环境部等在内的众多先进数值预报中心，都采用了非常先进的高性能计算机与高计算效率的数值预报系统，来进行业务数值预报。

作为我国专门从事大气海洋环境数值预报技术研究与系统研制的单位之一，国防科技大学从20世纪80年代起即开始进行数值预报系统研发，并深刻认识到并行计算技术在数值预报实时性问题中的重要地位并进行了长期的技术积累。但自2017年学校进行重新组建并重组气象海洋学院以来，一方面是随着模式分辨率的不断提升与模式本身复杂性的不断提高，并行计算技术在数值预报中的重要性有增无减。另一方面，既没有专门针对数值预报并行计算的本科生课程，也尚未在学校层面开设并行计算技术方面的公共课程。正是在该背景之下，在进行大气科学专业课程体系重新设计时，规划了并行计算技术课程，制订了相应的教学计划，并自2018级本科生起开始实施，旨在使学员掌握基本的并行計算技术，为利用数值预报进行气象海洋环境保障提供理论基础和技术支撑。

在进行课程内容设计时，一个很自然的想法是对相关课程进行模块化设计。模块化教学思想首先由德国与美国高校提出，但主要用于课程体系按模块来进行构建[1]，旨在将理论教学与生产实践有机融合，针对不同培养目的开展教学活动，以培养能够具备社会实际需要的应用复合型人才[2]。国内在采用模块化对课程教学内容进行设计方面也进行了不少研究。余国江[3]针对高校转型的需要，分析了其核心问题即课程转型的紧迫性、模块化课程的特点及其在转型中的作用，并从宏观、中观、微观三个层次进行了模块构建途径研究。屈婉玲等[4]对离散数学课程教学内容按知识单元进行模块化设置，以根据培养目标进行教学内容的灵活组织。魏英[5]在深入分析大学计算机基础课程教学所存在问题的基础上，根据各部分内容相对独立的特点，对分层模块化教学模式进行了研究。兰长林等[6]采取课程内容模块化和教师讲授、专题报告研究型教学模块化相结合的方式，开展了模块化教学方法研究。这些对模块化教学的研究，主要侧重于对课程内容的模块化组织，而对模块间所涉知识点的相互关系考虑较少。

对知识点或模块间关系的研究上，王燕等[7]针对网络课程，提出了利用概念图进行教学内容的建构与组织的方法，以避免教学内容出现概念孤立化与知识碎片化的问题，其围绕不同主题按树形结构进行知识组织，并通过相关主题、节点的展开与链接，论述了扩充学习、加深学习与补救学习的概念。陈雅[8]以认知弹性理论为指导，采用知识结构图与超文本技术相结合编排教学内容的序列与链接，探讨了网络课程教学内容的组织与呈现，其分析了将课程名称作为根节点的知识点间有向无环树形结构组织形式，以及基于知识点间从属与先决关系的排序结构。唐明[9]将教学内容具体化为知识点集合，并对知识点采用串行递推关系与并行递推关系进行层次关系建模分析。这些研究涉及到了知识点间的相关关系，并部分提到采用树形与网络等方式进行知识组织的思想，但很少涉及如何进行具体组织的问题。

本文针对并行计算技术课程教学内容，在目前已有知识点按模块进行组织的基础上，针对教学内容过多、各知识点间讲授先后顺序不太合理等问题，在对教学内容按知识点进行划分的基础上，利用图论技术进行知识点间依赖关系分析，再基于教学目标牵引对教学内容进行精简，并对各教学模块内容进行重组，以改进对课程教学内容的设置。

一  教学内容基于图论的模块化优化設计

目前，并行计算技术课程的教学内容组织为两大部分共6个模块，其中第一部分主要侧重于理论知识，包括并行计算基本概念、并行计算所涉软硬件基础、并行计算基本原理与方法3个模块；第二部分侧重于实践，包括并行计算环境基础、OpenMP并行编程基础、MPI并行编程基础3个模块。

第一部分的知识中，并行计算基本概念模块包括并行计算的意义、并行计算思维、并行处理的三要素、问题规模、并行度、任务分解、数据相关性、机器规模、任务调度、负载平衡、并行执行时间、并行开销、加速比、并行效率、同步、死锁、Amdahl定律和Gustafson定律等知识点；并行计算所涉软硬件基础模块包括并行计算存储结构、并行计算互连结构、并行计算模型和并行计算软件基础等知识点；并行计算基本原理与方法模块包括数据并行设计模式、任务分解概述、输出数据划分技术、输入数据划分技术、任务调度概述、块分布调度方法、循环块分布调度方法、分布存储并行计算原理、SPMD与MPMD、问题规模的影响、并行度的影响、通信次数的影响、计算通信重叠的影响、共享存储并行计算原理、指导语句数的影响和访存冲突的影响等知识点。

第二部分的知识中，并行计算环境基础包括Redhat Linux基础环境、gcc编译器及其安装、OpenMP并行计算环境验证、MPI并行计算环境配置和MPI并行计算环境验证等知识点；OpenMP并行编程基础包括OpenMP简介、动态域与静态域、OpenMP编译指导语句格式、OpenMP中的条件编译、OpenMP中的parallel语句、OpenMP中的for指导语句、OpenMP中的同步指导语句、OpenMP中的函数和OpenMP中的环境变量等知识点；MPI并行编程基础包括MPI简介、MPI程序的一般结构、MPI中的6个基本函数、MPI中的点对点通信、MPI中的数据类型、MPI中聚合通信操作、Jacobi迭代的并行计算和WRF模式的并行计算等知识点。

现在对并行计算技术课程所有知识点之间的依赖关系进行建模，当知识点A的讲授需要以先讲授知识点B为前提时，称知识点A依赖于知识点B。例如，“并行开销”依赖于“并行计算思维”“并行执行时间”“机器规模”“负载平衡”与“同步”。这样，每个知识点可能依赖于其他的知识点。由于进行上述知识点的划分时，知识点已经足够细到彼此之间不会出现相互依赖，即如果知识点A依赖于知识点B，则知识点B不可能反过来再依赖于知识点A，因此，如果知识点A依赖于知识点B，就引一条从知识点A到知识点B的边，则所有知识点之间的依赖关系给出的是一个有向无回路图[10]。

在按上述方式进行建模时，所得到的有向无回路图G中可能由于依赖关系较复杂，导致边数很多，而使得有向无回路图显得相当杂乱，不便进行后续分析。另一方面，我们在进行知识点讲授时，只需要知道知识点之间有依赖路径即可，而并无必要考虑每个知识点依赖的所有其他知识点。换句话说，如果图中存在从知识点A到知识点B的一条有向路径，则意味着已经得知知识点A需要在知识点B讲授完之后才能进行讲授，因此，此时知识点A到知识点B之间的有向边完全没有必要给出。假设知识点个数为n，如果将图G对应到一个逻辑矩阵M，并对知识点进行标号，第k个知识点对应于图G中的结点k，第i个知识点依赖于第j个知识点则m_ij取值为真，否则取值为假，则可以通过依次计算M¹、M²直到Mⁿ并检查每2个知识点间是否出现路径，并在出现路径时直接删除其间可能存在的有向边。

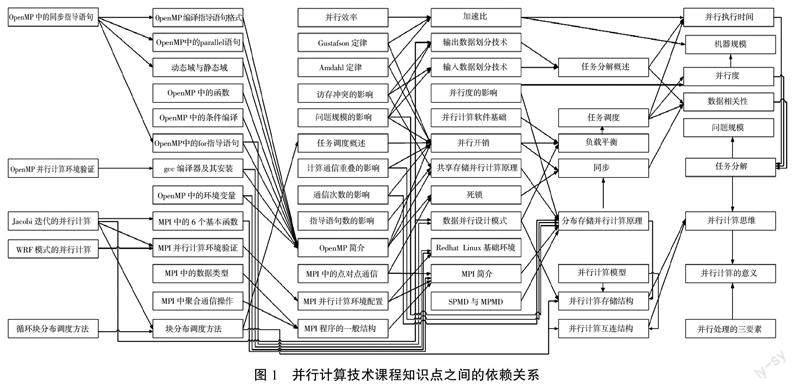
在如上处理后，并行计算技术课程各知识点之间的依赖关系进行了大幅简化，具体如图1所示。从图1清晰可见，知识点讲授时应严格遵循的先后顺序。例如，在讲授“同步”之前，先要讲授“数据相关性”，而在此之前，又要先讲授“任务分解”，而在讲授“任务分解”之前，又必须先讲授“问题规模”与“并行计算思维”。此外，如果课时有限，从图1中可以清晰地发现哪些知识点不会被其他知识点所依赖，在这些知识点对教学目标的实现不太重要时，即完全可以直接删除以进行内容的精简。对并行计算技术课程，教学目标主要是使学员掌握基本的并行计算技术，为利用数值预报进行气象海洋环境保障提供理论基础和技术支撑，而具体编程实践实际上是永无止境的，只要引学生入门即可。鉴于总课时数只有24学时，且从前几年的实际经验看，目前课程内容过多，确需压减课堂内容，为此，结合图1，显然易见，可以压减其中“Amdahl定律”“Gustafson定律”“并行计算模型”“动态域与静态域”“OpenMP编译指导语句格式”“OpenMP中的条件编译”“OpenMP中的同步指导语句”“OpenMP中的函数”“MPI中的数据类型”和“MPI中聚合通信操作”等知识点。

此外，通过图1所示的有向无回路图，还可以检查目前各模块中知识点设置的合理性，即可以检查在进行课程内容教学实施时，知识点之间的依赖关系是否能够得到满足。显然，目前大部分知识点在模块中的归属是合理的，但“OpenMP简介”原来安排在“MPI并行编程基础”模块进行介绍，实际上在“并行计算环境基础”模块的“OpenMP并行计算环境验证”知识点之前应该讲授，否则，将造成模块之间的相互依赖关系，引起教学实施上的不顺畅。“MPI简介”也具有类似问题。因此，“OpenMP简介”与“MPI简介”这2个知识点应分别从“OpenMP并行编程基础”“MPI并行编程基础”移到“并行计算环境基础”模块中，使得“并行计算环境基础”模块的知识点依次包括“Redhat Linux基础环境”“OpenMP简介”“gcc编译器及其安装”“OpenMP并行计算环境验证”“MPI简介”“MPI并行计算环境配置”和“MPI并行计算环境验证”。此外，在每个模块内，知识点之间也应遵循图1所给出的严格顺序关系，例如，对“并行计算基本概念”模块中知识点进行讲授时，部分需要进行先后顺序的重新安排。在综合考虑内容精简与知识点的重新组织后，优化前后各模块中知识点的教学实施顺序见表1，其中，无论对两模块还是两知识点，列于前者应该先行进行教学实施。

二  结束语

并行计算技术课程虽然在开设时，已经按模块化方式进行了教学计划的详细设计，但在教学实施过程中发现还存在教学内容过多、各知识点之间逻辑关系不十分清晰、讲授顺序不太合理等问题，本文通过对知识点依赖关系采用有向无回路图进行建模，采用从图中去除对教学目标影响小且不被依赖的知识点来缩减教学内容、基于图中知识点间依赖关系对模块间与模块内知识点进行重组的方法，对教学内容的精简与重组进行了优化设计。

参考文献：

[1] 米洁，黄民.基于模块化知识体系的创新实践能力培养教学改革[J].中国大学教学，2014（9）：37-40.

[2] 于婷婷.“互联网+”视域下高校模块化教学探究[J].中国成人教育，2018（4）：89-91.

[3] 余国江.课程模块化：地方本科院校课程转型的路径探索[J].中国高教研究，2014（11）：99-102.

[4] 屈婉玲，王元元，傅彦，等.“离散数学”课程教学实施方案[J].中国大学教学，2011（1）：39-41.

[5] 魏英.大学计算机基础分层模块化教学改革研究与实践[J].西北工业大学学报（社会科学版），2012，32（3）：105-106.

[6] 兰长林，赵江涛，崔莹，等.“模块化”教学法在《原子核物理学》课程中的探索与应用[J].教育教学论坛，2019（18）：215-216.

[7] 王燕，周艳洁.基于概念图的网络课程教学内容的组织探究[J].软件导刊（教育技术），2014，13（12）：5-7.

[8] 陈雅.基于认知弹性理论的网络课程教学内容的组织[J].中国成人教育，2014（13）：141-143.

[9] 唐明.面向复杂工程问题的高校课堂教学内容组织方法浅论[J].教育现代化，2019，6（80）：227-228.

[10] 吴建平，王正华，李晓梅.稀疏线性方程组的高效求解与并行计算[M].长沙：湖南科学技术出版社，2004.