基于财务信息和非财务信息的债券违约预警模型研究
2023-06-11郑煜吴世农
郑煜 吴世农


【摘要】自2014年我国债券市场发生首例债券违约以来, 债券违约事件日益增多。尤其近几年来, 无论是发生债券违约的企业、 债券违约的只数还是违约总金额, 都呈现爆发式增长和蔓延态势。在此背景下, 本文使用2014 ~ 2020年债券市场全样本数据, 基于财务信息构建债券违约预警模型, 在Fisher模型与Logistic模型判别效果对比后选择了Logistic模型, 并在此基础上加入部分非财务信息指标, 以进一步提升模型的预测能力。最终得到基于财务和非财务信息的Logistic模型。研究结论如下: 第一, Logistic模型整体判别效果优于Fisher模型。第二, 构建的基于财务和非财务信息的Logistic模型具有较好的预测能力, 经济含义清晰, 具备实际使用价值。第三, 财务指标如净资产收益率、 资本累积率、 刚性负债率、 筹资NCF/平均总资产等是债券违约预警模型中的显著指标, 这些指标对于预警债券违约具有重要作用。第四, 部分非财务指标对于提升模型预警能力有明显效果, 非财务信息诸如发债企业所在省份风险情况、 行业风险情况、 企业所有制形式等为预警债券违约提供了显著的增量信息, 也反映了我国债券违约具有所有制、 地域和行业的群聚特征。
【关键词】债券违约;预警模型;财务信息;非财务信息
【中图分类号】F275 【文献标识码】A 【文章编号】1004-0994(2023)12-0022-8
一、 引言
自2014年我国债券市场发生首例违约以来, 债券违约事件频发。据Wind数据库统计, 2018年我国信用债券违约总额已達1209.1亿元, 大于2014 ~ 2017年四年之和。2019年债券违约总额为1444.08亿元, 相较2018年进一步增加。从历史上来看, 欧债危机、 美国次贷危机等都源于债券市场大面积违约, 一度使得全球经济陷入危机。
企业破产、 财务困境和债券违约的预警研究源于20世纪60年代(Beaver,1966;Altman,1968), 我国在这方面的研究也已有30多年的历史(吴世农和黄世忠,1987), 后续研究(陈静,1999;张玲,2000;吴世农和卢贤义,2001)主要在2000年前后。近年来, 对这一课题的新研究并不多。最近的研究发现, 随着我国债券市场的发展, 发债企业、 债券种类和债券发行量越来越多, 但债券违约事件频发, 不仅债券违约数量大幅增加, 种类多元, 而且违约债券的信用级别呈现上升趋势, 涉及的企业类型、 所属行业和地区也越来越多(吴世农等,2021)。因此, 如何识别、 预警、 防范债券违约风险, 构建具有信息含量的高效的债券预警模型, 成为债券违约预警研究的热点问题。
本文以我国2014 ~ 2020年所有发生债券违约的发债企业和所有未发生债券违约的发债企业为样本, 收集相关财务信息和非财务信息, 应用Fisher判定模型和Logistic判定模型构建我国债券违约的预警模型。研究结果表明, 本文所构建的债券违约预警模型具有较强的解释能力和较高的预测精度, 为现有债券违约风险管理提供了新的依据和工具。
本文的主要边际贡献在于: 一是探讨财务预警指标及其滞后年限与债券违约预警模型准确率之间的关系, 为如何选择财务指标用于债券违约的预警模型提供新的思路。二是指出哪些指标对于债券违约预警具有重要意义。三是在根据财务信息构建债券违约预警模型的基础上, 探讨引入非财务信息(包括企业所有制、 企业所在省份与所在行业风险情况和宏观经济情况等), 是否可以有效地提高债券违约预警模型的准确度。
二、 文献综述
债券违约的原因比较复杂, 往往是内外因、 财务与非财务因素等相互作用影响下最终导致债券违约。从债券违约的影响因素来看, 已有研究发现主要是财务、 经营、 公司治理和行业及宏观经济因素等。因此, 早期的债券违约预警模型主要基于财务和经营因素, 此后陆续发现债券违约具有行业特征、 公司治理特征, 同时与经济周期具有显著的关系。从债券违约的研究方法来看, 先后应用简约模型、 结构模型、 统计线性判别分析、 非线性判别分析等传统的统计模型, 以及近年来使用基于机器学习方法的人工神经网络(ANN)、 支持向量机模型(SVM)和集成学习模型(ELM)等。相比传统统计方法构建的债券违约预警模型, 目前基于机器学习方法的债券预警模型在准确度方面有明显的优势(吴世农等,2021), 但较难以解释债券违约的成因, 也因此难以提出相应的对策。
我国首例债券违约发生的时间较晚, 且债券市场集中爆发违约也只是近几年的现象, 因此债券违约预警模型的相关研究近几年才引起广泛的关注。目前, 债券违约预警模型的研究需要解决三个主要问题: 一是财务预警指标的选择; 二是非财务预警指标的选择; 三是预警模型的选择。
(一)预警指标的选择
1. 财务预警指标。Beaver(1966)、 Altman(1968)、 Ohlson(1980)、 吴世农和黄世忠(1987)、 王春峰等(1998)、 陈静(1999)、 张玲(2000)、 吴世农和卢贤义(2001)、 方洪全等(2004)、 郭斌等(2006)、 Chen和Hsiao(2008)、 Xiao等(2012)在财务危机或企业信用风险预警时较多选取的财务指标包括: 资产负债率、 ROE、 流动比率、 营运资本/总资产、 总资产周转率、 应收账款周转率、 EBIT/总资产、 留存收益/总资产等。Altman和Brenner(1981)、 Clark和Weinstein(1983)发现并证实了除传统财务指标外, 企业股票的收益率等也能对企业财务危机起到预警作用。另外, Aziz等(1988)、 张友棠(2004)、 蔡基栋和晏静(2004)的研究从不同方面证明了现金流量相关指标对提高预警模型准确度和稳定性具有显著作用。现有文献侧重于使用自由现金流或经营活动净现金流等指标, 而近年来我国出现的许多债券发行主体违约都涉及企业激进投资扩张或再融资困难等因素, 因此, 基于我国国情, 除现金流量相关指标以外, 还需深入探讨企业过度投资、 融资模式、 融资约束和融资净现金流对债券违约的影响。
2. 非财务预警指标。一般情况下, 非财务指标可以分为三类: 一是宏观经济指标; 二是行业和区域状况指标; 三是企业的非财务指标。
Alves(1978)率先提出, 需要将宏观经济指标纳入企业财务危机预警模型。Nam(2008)在对风险模型的拓展中创造了宏观依赖模型, 加入GDP增速指标, 大大增强预警模型的解释力。姚红宇和施展(2018)使用我国企业的样本数据证明了部分宏观经济指标和地方经济指标对于提高预警模型的精度有显著作用。尽管不少学者已经考虑到宏观经济指标对于企业财务危机或债务违约具有重要影响, 但近年来一些企业因宏观融资环境的骤然变化导致资金链断裂从而发生债券实质性违约的情形, 已有研究中所纳入的宏观经济指标并不能准确地进行解释和预测。Perry(1981)指出, 企业所处不同的行业将呈现截然不同的行业特征, 因此他将行业信息指标纳入预警模型作为重要变量。企业的非财务指标包括一系列定性和定量信息。郭斌等(2006)将消除行业影响后的行业相对财务指标以及加入银行的授信额度、 企业的贷款方式、 公司规模、 M2增长率、 CPI增长率等非财务指标引入模型, 发现模型的表现有所提升。姚红宇和施展(2018)在模型中引入了企业所有制形式和地方经济指标, 发现预测结果好于Altman模型。Liang等(2016)、 Wang等(2014)、 Brown(2012)、 杨海军和太雷(2009)发现加入一些公司治理变量可优化机器学习算法的分类能力, 或改进模型对不平衡样本的处理能力。
综上所述, 值得纳入考量的非财务预警指标包括: 从宏观角度看, 经济周期、 宏观经济政策的变化等; 从地区角度看, 当地经济发展状况、 社会资本等; 从行业角度看, 行业周期变化、 资产轻重、 其他行业信息指标等; 从微观角度看, 公司治理特征、 股权结构、 企业所有制形式、 法律纠纷等。
(二)预警模型的选择
此前学者主要使用传统的统计分析方法构建模型进行财务危机、 企业违约的预警或信用风险分析, 包括结构模型、 简约模型和判别模型。随着计算机科学和人工智能技术的发展, 现代人工智能方法也逐渐被用于构建预警模型。
在结构模型方面, Black和Scholes(1973)、 Merton(1974)提出使用期权定价理论构建结构化模型来评估企业的信用风险, 把公司价值作为影响债券是否违约的重要因素。但由于我国债券市场违约历史并不长, 违约历史数据不充足, 且我国债券市场很多信用债券成交并不活跃, 价格发现机制很难充分发挥作用。其余结构模型如Black和Cox(1976)提出的首達违约模型(First Passage Model), 其前提假设条件是利率始终不变, 这与实际情况明显不符; 美国KMV公司建立的KMV模型, 其存在无法度量非上市公司的局限性。因此, 上述结构模型均较难实际运用于我国信用债券违约预警。
在简约模型方面, 此模型最早由Jarrow和Turnbull(1995)提出。他们认为债券违约是外生的, 违约只与公司的外部因素(如经济因素和统计价值)有关, 基于这个基本认识来计算违约率。此后, 学者主要从两方面研究违约强度: 一是分析违约强度的影响因素。Duffie与Lando(2001)、 Kay(2003)指出影响违约强度的因素可以分为宏观经济因素和企业自身因素, 一般后者对违约强度起主要作用。二是分析违约强度遵循的随机过程。研究发现, 简约模型在预测能力上并无显著优势。
在判别模型方面, 最早由Beaver(1966)提出了单指标判定模型, 而后Altman(1968)提出多指标判定模型(Z-score模型), Altman(1977)又基于Z-score模型提出了包含七个变量的ZETA模型。从统计学的角度, 上述模型均要求变量服从正态分布且相互独立, 两个不同主体有各自的均值但有相同的方差—协方差矩阵等条件, 这与现实情况往往不完全一致。而后, Ohlson(1980)提出的Logistic模型、 Zmijewski(1984)引入的与Logistic模型相似的Probit模型, 使得上述假设条件得以放宽, 模型预测准确度也被证明有所提高。此后许多研究亦证明Logistic模型具有较好的预警效果(吴世农和卢贤义,2001)。
在基于机器学习的预警模型方面, Odom和Sharda(1990)、 Coat和Fant(1993)、 Altman等(1994)、 杨淑娥和黄礼(2005)等学者的研究均表明神经网络分析法有较好的预测效果。Varetto(1998)使用遗传算法来进行企业财务危机预警, 但发现预警准确度较低。Dimitras等(1999)使用粗糙集理论进行企业财务危机预警, 但在实践中粗糙集方法抗干扰能力较差, 因而其更多是与其他基于机器学习的方法如神经网络分析等结合使用。Corinna Cortes和Vapnik(1995)提出支持向量机理论, 而后Fan和Palaniswami(2000)率先运用该理论方法进行企业财务危机预警, 取得了良好的预警效果。Barboza等(2017)以 1985 ~ 2013 年美国上市公司为样本, 比较了传统的统计模型和机器学习模型对公司破产的预测精度。吴世农等(2021)以2014 ~ 2020年发债企业为样本, 比较两种基于统计判定方法的预警模型和三类基于机器学习的七种预警模型的准确度。近年来, 国内许多学者尝试优化神经网络或支持向量机并进行预警研究, 如杨旸和林辉(2016)、 阎娟娟等(2006)。但此前被证明有较好预警效果的神经网络方法和支持向量机等方法, 是一种“数据驱动”模型, 实际上对数据量有很高的要求, 若借鉴运用于我国信用债券预警则需要有较多的历史违约数据积累。此外, 基于机器学习所构建的预警模型一个明显的缺陷是其运算过程缺乏透明度, 目前除了基于随机森林算法的决策树模型能够度量出变量的“重要性”, 其他基于机器学习算法的预警模型均难以解释债券违约的成因并提出对策。
(三)文献评述
首先, 债券违约的研究不等于企业破产或企业ST的研究。国内外诸多学者对企业信用风险度量、 企业违约、 企业财务困境等展开了较为丰富的研究, 使用的研究方法全面而深入, 但主要选取的是ST与非ST企业, 或破产企业和正常企业作为实证研究的样本。在我国, 企业ST或企业破产, 不能完全等同于债券违约。很多发债企业并未上市, 也有部分上市ST企业从未在债券市场发行过债券, 因此以ST公司为样本构建的预警模型, 不能简单等同于债券违约预警模型。同样地, 企业很可能在面临破产清算之前, 在债券市场发行的债券就已经发生了实质性违约; 还有的企业尽管发生了债券违约, 但其后在各方协调或者第三方注资情况下, 很快恢复了正常生产经营, 那么企业最终也不会破产。总之, 基于ST企业或破产企业构建的企业违约预警模型与债券违约预警模型, 研究方法相似, 但在影响因素和指标选择方面却不完全相同。
其次, 当前一部分发债企业主要依靠融资还债, 即“借新还旧”。也有部分发生债券违约的企业在违约前几年扩张过快, 投资活动净现金流大幅流出, 导致企业没有足够的货币现金用于债券的付息还本, 从而形成债券违约。此外, 近年来国有企业与民营企业所发行债券违约率的分化日益明显, 行业间、 地区间的债券违约情况也有所不同。但是, 传统的信用风险评价模型、 违约模型或是财务困境预警模型选用的财务指标多关注企业盈利能力、 资产流动性、 资产使用效率、 负债比例、 偿债能力、 经营活动现金流等, 却可能忽视了现实经济生活中企业还债的另一直接来源——筹资活动净现金流, 也可能忽略了快速扩张企业的投资活动净现金流的持续大幅度流出。此外, 在非财务因素方面, 现有文献也很少考虑具有中国特色的企业所有制形式等因素。因此, 在以往文献普遍关注的资产负债率、 ROE、 流动比率、 营运资本/总资产、 总资产周转率、 应收账款周转率、 EBIT/总资产、 留存收益/总资产、 经营活动净现金流/总资产等指标的基础上, 应加强对于企业筹资活动净现金流、 投资活动净现金流, 以及发债企业的所有制形式、 所处行业和地区等非财务信息的研究。
最后, 在预警模型选择方面, 尽管过往文献先后使用简约模型、 结构模型或现代人工智能方法, 但也发现简约模型在预测上并无显著优势。结构模型较难实际运用于我国的债券违约预警。基于机器学习方法的预警模型对数据量的要求较高, 且往往難以解释债券违约的成因或指标变量的重要性和意义。因此, 在债券违约的预警模型中, 统计判别模型仍是目前已被证明预测效果良好、 解释能力较强的预警模型, 也是目前探讨基于大数据构建的机器学习方法的预警模型的比较基准。
三、 研究设计: 研究样本、 预警指标和研究方法
(一)研究样本的选取
本文数据来源于Wind数据库。以我国债券市场上发行信用债的企业为实证研究对象, 信用债指依据Wind分类的一般公司债、 私募债、 一般企业债、 定向工具、 短期融资券、 超短期融资券、 中期票据等七类债券。本文所指的债券违约严格定义为企业主体公告其发行的债券实质违约。若有某个企业主体多次债券违约, 则以其首次债券违约为准。
鉴于我国首笔信用债违约发生在2014年, 本文选取的考察时间区间为2014年1月 ~ 2020年12月。使用该区间的全样本数据构建模型, 提取样本区间每年当年债券市场上全部符合要求的、 有存量债券的、 信用评级在BBB级以上尚未发生债券违约的全部发债企业作为“正常企业”, 以及当年发生首笔债券违约的“债券违约企业”进行研究。随机抽取“正常企业”与“债券违约企业”各80%作为“训练样本”构建模型, 剩余20%的“正常企业”与“债券违约企业”作为测试样本。
此外, 考虑到城投企业和金融企业财务报表的特殊性, 选取样本时剔除这两类企业; 还将删除重复样本、 部分财务与非财务信息缺失的样本。
记企业发生首次债券违约的年份为t年、 违约发生前1年为t-1年、 违约发生前2年为t-2年。酌情删除信息缺失的发行主体后, t-1年选取正常企业样本共1748个, 债券违约企业样本共83个作为“训练样本”; t-2年选取正常企业样本共1580个, 债券违约企业样本共68个作为“训练样本”。
(二)预警指标的选取
发债企业最终发生债券违约, 可能是由于多方面因素造成的, 但首先表现出来的是其财务状况逐步恶化。因此, 本文首先选取财务指标构建模型, 在后续的模型改进中再引入非财务指标。本文选取的财务指标包括反映企业的盈利能力、 现金创造能力、 负债比例、 偿债能力、 资产流动性、 资产周转速度、 成长能力、 投融资情况共八大方面43个财务指标。上述经典文献及近年文献中所提到的财务指标基本都包含在这八大方面43个财务指标中。之后的研究中, 就以这43个财务指标作为待选变量进行筛选后引入预警模型。43个指标分别用x1、 x2、 x3、 …、 x48表示。八大类共43个指标列示如下。
1. 盈利能力相关指标。包括总资产收益率ROA(x1)、 净资产收益率ROE(x2)、 财务费用率(x3)、 总资产净利润率(x4)、 营业毛利率(x5)、 销售净利率(x6)、 流动资产净利率(x7)、 固定资产净利率(x8)、 营业利润率(x9)。
2. 现金创造能力指标。包括销售创现率(x10)、 资产创现率(x11)、 权益创现率(x12)、 利润的现金含量(x13)、 现金及其等价物增加额/总资产(x14)、 现金资产/总资产(x15)。
3. 负债比例指标。包括资产负债率(x16)、 刚性负债率(x17)、 流动负债比率(x18)。
4. 偿债能力指标。包括本息保障倍数(x19)、 EBIT本息保障倍数(x20)、 EBITDA本息保障倍数(x21)、 利息保障倍数(x22)、 EBIT利息保障倍数(x23)、 EBITDA利息保障倍数(x24)。
5. 资产流动性指标。包括流动比率(x25)、 速动比率(x26)、 超速动比率(x27)、 现金比率(x28)、 营运资本比率(x29)、 营运资本/总资产(x30)、 产权比率(x31)、 固定资产比率(x32)、 流动资产比率(x33)。
6. 周转速度指标。包括总资产周转率(x34)、 流动资产周转率(x35)、 营运资本周转率(x36)、 固定资产周转率(x37)、 应收账款周转率(x38)、 存货周转率(x39)、 應付账款周转率(x40)。
7. 成长能力指标。仅包括资本累积率(x41)。
8. 投融资情况指标。包括筹资NCF/平均总资产(x42)、 投资NCF/平均总资产(x43)。
(三)研究程序和研究方法
本文首先引入上述指标, 使用向前逐步回归法分别构建t-1年、 t-2年债券违约预警模型。使用统计判定分析方法为Fisher模型和Logistic模型, 并比较两个模型的预测效果。而后在Logistic预警模型的基础上加入非财务指标, 构建基于财务和非财务信息的新Logistic模型, 并使用测试样本对该模型预测能力进行检验, 得到适用于实际预测的最终模型。
四、 债券违约预警模型的实证研究及其比较分析
(一)Fisher模型的构建与检验
1. t-1年Fisher模型的构建与检验。采用向前逐步回归法, 当F统计量显著性水平小于0.05时引入模型, 当其显著性水平大于0.10时从模型中剔除, 根据SPSS 21.0输出结果, 得到7个指标变量及其系数。这7个指标变量分别是营业利润率(x9)、 净资产收益率ROE(x2)、 资本累积率(x41)、 资产创现率(x11)、 筹资NCF/平均总资产(x42)、 刚性负债率(x17)、 现金及其等价物增加额/总资产(x14)。7个指标分别代表企业的盈利能力、 成长能力、 现金创造能力、 投融资情况、 负债比例。整理可得非标准化典型判别式函数:
式(1-1)就是t-1年的Fisher判别模型。对模型进行组均值均等性检验、 方差—协方差矩阵相等性检验、 多重共线性检验和模型整体显著性检验。组均值均等性检验结果显示, 模型中7个指标变量除资本累积率外, 其余6个指标的组均值均等性检验显著性均小于0.01, 说明类内均值具有显著性差异, 可用于判别分析; 资本累积率也有较低的显著性, 基本可用于判别分析。使用Box's M进行方差—协方差矩阵相等性检验, 其显著性水平为0.000, 拒绝了总体协方差矩阵相等的原假设, 因此使用合并的方差—协方差矩阵进行判别分析。多重共线性检验显示, 所有留在模型中的指标变量容差都较大, 而方差膨胀因子VIF都远小于10, 可见指标之间不存在严重的多重共线性。模型整体的显著性检验表明, 模型的Wilks的Lambda值为0.862, 相伴概率为0.000, 模型达到了显著性水平。
2. t-2年Fisher模型构建与检验。采用向前逐步回归法, 当F统计量显著性水平小于0.01时引入模型, 当F统计量显著性水平大于0.10时从模型中剔除。根据SPSS 21.0输出结果, 得到8个指标变量及其系数。这8个指标变量分别是: 净资产收益率ROE(x2)、 总资产净利润率(x4)、 固定资产比率(x32)、 利润的现金含量(x13)、 筹资NCF/平均总资产(x42)、 投资NCF/平均总资产(x43)、 刚性负债率(x17)、 现金及其等价物增加额/总资产(x14)。8个指标分别代表了企业的盈利能力、 资产流动性、 现金创造能力、 投融资情况、 负债比例。整理可得如下非标准化典型判别式函数:
式(1-2)就是t-2年的Fisher判别模型。对模型进行组均值均等性检验、 方差—协方差矩阵相等性检验、 多重共线性检验和模型整体显著性检验。模型中4个指标变量的组均值均等性检验显著性均小于0.1, 说明类内均值具有显著性差异, 可用于判别分析。使用Box's M进行方差—协方差矩阵相等性检验, 其显著性水平为0.000, 拒绝了总体协方差矩阵相等的原假设, 因此使用合并的方差—协方差矩阵进行判别分析。多重共线性检验显示, 所有留在模型中的指标变量容差都较大, 而方差膨胀因子VIF都远小于10, 可见指标之间不存在严重的多重共线性。模型整体的显著性检验表明, 模型的Wilks的Lambda值为0.832, 相伴概率为0.000, 模型达到了显著性水平。
3. Fisher模型判别能力检验。将正常企业定义为组合0, 将发生债券违约的企业定义为组合1, 查找SPSS结果, 可以得到各年模型的判定结果。各年模型判定结果和准确率如表1所示。
总体来看, 违约发生前两年的Fisher模型对于正常企业的判断效果良好, 但对于债券违约企业判别正确率较低, 整体判别正确率一般。
(二)Logistic模型的构建与检验
1. t-1年Logistic模型构建与检验。采用向前逐步回归方式构建Logistic回归模型, 筛选指标变量的标准为: 当F统计量显著性水平小于0.01时引入模型, 当F统计量显著性水平大于0.10时从模型中剔除。最终得到净资产收益率ROE(x2)、 现金资产/总资产(x15)、 销售净利率(x6)、 固定资产比率(x32)、 筹资NCF/平均总资产(x42)、 刚性负债率(x17)、 现金及其等价物增加额/总资产(x14)共7个指标变量进入模型, 7个指标分别代表企业的盈利能力、 资产流动性、 投融资情况、 负债比例、 现金创造能力。最后得到的7个指标都在0.01的水平上显著。
再结合常数项-4.861, 可以得到以下t-1年的Logistic回归方程:
式(1-4)即为t-1年的违约概率方程。对模型进行多重共线性检验和整体显著性检验。多重共线性检验显示, 所有留在模型中的指标变量容差都较大, 而方差膨胀因子VIF都远小于10, 可见指标之间不存在严重的多重共线性。使用卡方检验对Logistic回归方程式(1-4)进行检验。根据SPSS 21.0的结果, 得到模型卡方值为195.879, 模型显著性水平为0.000, 拒绝了各个系数为0的原假设, 表明模型是显著的。
2. t-2年Logistic模型构建与检验。采用向前逐步回归方式构建Logistic回归模型, 筛选指标变量的标准为: 当F统计量显著性水平小于0.01时引入模型, 当F统计量显著性水平大于0.10时从模型中剔除。最终得到财务费用率(x3)、 应付账款周转率(x40)、 流动资产比率(x33)、 筹资NCF/平均总资产(x42)、 刚性负债率(x17)共5个指标变量进入模型, 5个指标分别代表了企业的盈利能力、 资产周转速度、 流动性、 投融资情况、 负债率。最后得到的5个指标除流动资产比率(x33)外都在0.01的水平上显著, 而流动资产比率(x33)则在0.05的水平上显著。
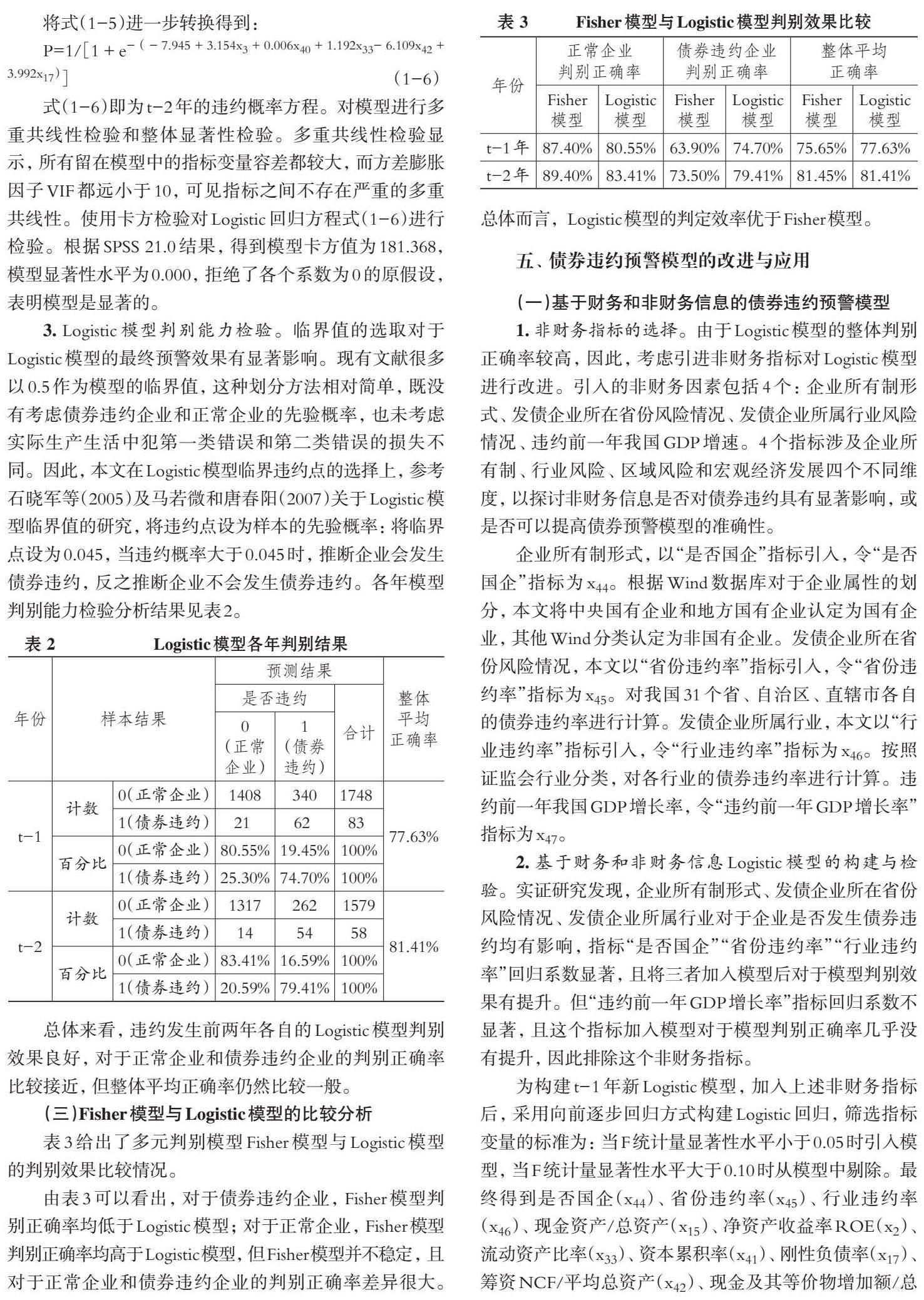
式(1-6)即为t-2年的违约概率方程。对模型进行多重共线性检验和整体显著性检验。多重共线性检验显示, 所有留在模型中的指标变量容差都较大, 而方差膨胀因子VIF都远小于10, 可见指标之间不存在严重的多重共线性。使用卡方检验对Logistic回归方程式(1-6)进行检验。根据SPSS 21.0结果, 得到模型卡方值为181.368, 模型显著性水平为0.000, 拒绝了各个系数为0的原假设, 表明模型是显著的。
3. Logistic模型判别能力检验。临界值的选取对于Logistic模型的最终预警效果有显著影响。现有文献很多以0.5作为模型的临界值, 这种划分方法相对简单, 既没有考虑债券违约企业和正常企业的先验概率, 也未考虑实际生产生活中犯第一类错误和第二类错误的损失不同。因此, 本文在Logistic模型临界违约点的选择上, 参考石晓军等(2005)及马若微和唐春阳(2007)关于Logistic模型临界值的研究, 将违约点设为样本的先验概率: 将临界点设为0.045, 当违约概率大于0.045时, 推断企业会发生债券违约, 反之推断企业不会发生债券违约。各年模型判别能力检验分析结果见表2。
总体来看, 违约发生前两年各自的Logistic模型判别效果良好, 对于正常企业和债券违约企业的判别正确率比较接近, 但整体平均正确率仍然比较一般。
(三)Fisher模型与Logistic模型的比较分析
表3给出了多元判别模型Fisher模型与Logistic模型的判别效果比较情况。
由表3可以看出, 对于债券违约企业, Fisher模型判别正确率均低于Logistic模型; 对于正常企业, Fisher模型判别正确率均高于Logistic模型, 但Fisher模型并不稳定, 且对于正常企业和债券违约企业的判别正确率差异很大。总体而言, Logistic模型的判定效率优于Fisher模型。
五、 债券违约预警模型的改进与应用
(一)基于财务和非财务信息的债券违约预警模型
1. 非财务指标的选择。由于Logistic模型的整体判别正确率较高, 因此, 考虑引进非财务指标对Logistic模型进行改进。引入的非财务因素包括4个: 企业所有制形式、 发债企业所在省份风险情况、 发债企业所属行业风险情况、 违约前一年我国GDP增速。4个指标涉及企业所有制、 行业风险、 区域风险和宏观经济发展四个不同维度, 以探讨非财务信息是否对债券违约具有显著影响, 或是否可以提高债券预警模型的准确性。
企业所有制形式, 以“是否国企”指标引入, 令“是否国企”指标为x44。根据Wind数据库对于企业属性的划分, 本文将中央国有企业和地方国有企业认定为国有企业, 其他Wind分类认定为非国有企业。发债企业所在省份风险情况, 本文以“省份违约率”指标引入, 令“省份违约率”指标为x45。对我国31个省、 自治区、 直辖市各自的债券违约率进行计算。发债企业所属行业, 本文以“行业违约率”指标引入, 令“行业违约率”指标为x46。按照证监会行业分类, 对各行业的债券违约率进行计算。违约前一年我国GDP增长率, 令“违约前一年GDP增长率”指标为x47。
2. 基于财务和非财务信息Logistic模型的构建与检验。实证研究发现, 企业所有制形式、 发债企业所在省份风险情况、 发债企业所属行业对于企业是否发生债券违约均有影响, 指标“是否国企”“省份违约率”“行业违约率”回归系数显著, 且将三者加入模型后对于模型判别效果有提升。但“违约前一年GDP增长率”指标回归系数不显著, 且这个指标加入模型对于模型判别正确率几乎没有提升, 因此排除这个非财务指标。
为构建t-1年新Logistic模型, 加入上述非财務指标后, 采用向前逐步回归方式构建Logistic回归, 筛选指标变量的标准为: 当F统计量显著性水平小于0.05时引入模型, 当F统计量显著性水平大于0.10时从模型中剔除。最终得到是否国企(x44)、 省份违约率(x45)、 行业违约率(x46)、 现金资产/总资产(x15)、 净资产收益率ROE(x2)、 流动资产比率(x33)、 资本累积率(x41)、 刚性负债率(x17)、 筹资NCF/平均总资产(x42)、 现金及其等价物增加额/总资产(x14)共10个指标变量进入t-1年的模型。
式(1-7)即为t-1年考虑财务和非财务信息的新Logistic模型, 式(1-8)即为t-1年的违约概率方程。对模型进行多重共线性检验和整体显著性检验。多重共线性检验结果表明, 所有留在模型中的指标变量容差都较大, 而方差膨胀因子VIF都远小于10, 可见指标之间不存在严重的多重共线性。使用卡方检验对Logistic回归方程式(1-8)进行检验。根据SPSS 21.0检验结果, 得到模型卡方值为263.305, 模型显著性水平为0.000, 拒绝了各个系数为0的原假设, 表明模型是显著的。
为构建t-2年新Logistic模型, 采用向前逐步回归方式构建Logistic回归模型, 筛选指标变量的标准为: 当F统计量显著性水平小于0.05时引入模型, 当F统计量显著性水平大于0.10时从模型中剔除。最终得到省份违约率(x45)、 是否国企(x44)、 净资产收益率ROE(x2)、 固定资产比率(x32)、 资本累积率(x41)、 筹资NCF/平均总资产(x42)、 刚性负债率(x17)共7个指标变量进入模型。最后得到的7个指标均在0.01的水平上显著。
式(1-9)即為t-2年考虑财务和非财务信息的新Logistic模型, 式(1-10)即为t-2年的违约概率方程。对模型进行多重共线性检验和整体显著性检验。多重共线性检验显示, 所有留在模型中的指标变量容差都较大, 而方差膨胀因子VIF都远小于10, 可见指标之间不存在严重的多重共线性。使用卡方检验对Logistic回归方程式(1-10)进行检验。根据SPSS 21.0结果, 得到模型卡方值为243.381, 模型显著性水平为0.000, 拒绝了各个系数为0的原假设, 表明模型是显著的。
考虑非财务信息的新Logistic模型的判别能力检验结果见表4。由表4可以看到, 该模型判别正确率较高。
表5进一步列出了考虑非财务信息的新Logistic模型(表中为“新L模型”)与原Logistic模型(表中为“原L模型”)的判别效果比较结果。可以看出, 新Logistic模型判别准确率相比于原Logistic模型在各个年份均有显著提升, 特别是发债违约企业最后判定为债券违约企业的准确性大幅上升且更加稳定。可见, 非财务信息包括企业所有制、 地域债券违约风险和行业债券违约风险等具有预测企业债券是否违约的增量信息, 也揭示了我国债券违约具有所有制、 地域和行业的群聚特征。
(三)债券违约预警模型的应用
为检验改进后的考虑非财务信息的新Logistic模型的实际应用效果, 本文使用测试样本对模型进行实际应用能力测试。
本文使用2014年1月 ~ 2020年12月的全样本数据构建模型, 提取该期间内每年当年债券市场上全部符合要求的、 有存量债券的、 信用评级在BBB级以上尚未发生债券违约的全部发债企业作为“正常企业”, 以及当年发生首笔债券违约的“债券违约企业”进行研究。同时剔除城投企业、 金融企业、 数据缺漏企业。随机抽取“正常企业”与“债券违约企业”各80%作为“训练样本”构建模型, 剩余20%的“正常企业”与“债券违约企业”作为测试样本。最终得到t-1年测试样本437家正常企业和20家债券违约企业, 得到t-2年测试样本397家正常企业和17家债券违约企业。预测结果见表6。由表6可以看出, 基于财务和非财务信息的新Logistic模型, 对于测试样本仍然保持了良好的预测能力。
六、 结论与启示
本文使用我国2014 ~ 2020年债券市场全样本数据, 以企业常用财务指标作为预警变量, 在采用向前逐步回归法筛选变量后, 分别构建了t-1年、 t-2年的Logistic模型和Fisher模型, 对两模型的判别效果进行了比较, 发现Logistic模型判别效果更优。在此基础上, 将企业所有制、 发债企业所在省份风险情况、 行业风险情况三个非财务指标纳入Logistic预警模型, 从而显著地提高了预测正确率。最后, 使用随机抽取的测试样本进行判定和预警, 再次验证了基于财务信息与非财务信息构建的新Logistic模型的预测效果更好, 更具备实用价值。本文提出的基于财务和非财务信息的新Logistic模型具有较好的预测能力, 经济含义清晰, 因此该模型具有实际使用价值。
此外, 还有以下几点启示。
第一, 本文提出的债券违约预警模型可以为债券投资机构风控部门的内部评级和投资部门的投资决策提供参考。模型可以预测各发债企业的违约概率, 为当前投资机构风控部门的内部评级提供参考。投资部门在进行投资决策时, 亦可根据模型给出的违约概率, 结合市场债券价差情况进行投资操作。
第二, 为相关政府部门决策提供依据。部门或区域内的企业如果集中出现债券违约, 将有可能引发部门或区域性风险。模型事先预测这些企业的债券违约概率, 将有利于相关政府部门提前做出部署, 以防范化解风险。同时, 如果部门或区域内企业大面积债券违约概率上升, 政府部门亦可及时查明原因, 调整政策。
第三, 向企业管理层发出债券是否发生违约的预警, 为预警查找原因。本文的预警模型能够及时向企业管理层发出预警, 使得企业尽早发现风险点, 及时采取对策, 改善经营和财务状况, 避免企业债券发生违约。
第四, 从各年预警模型可以看出, 净资产收益率、 资本累积率、 刚性负债率、 筹资NCF/平均总资产等财务指标是债券违约预警模型中的显著指标, 这些指标对于预警债券违约具有重要作用。
第五, 非财务指标对于提升模型预警能力有明显效果。非财务信息诸如发债企业所在省份风险情况、 行业风险情况、 企业所有制形式等在预警债券违约中提供了重要的增量信息, 这也反映了我国债券违约具有地域、 行业和所有制的群聚特征。
【 主 要 参 考 文 献 】
陈静.上市公司财务恶化预测的实证分析[ J].会计研究,1999(4):31 ~ 38.
郭斌,戴小敏,曾勇,方洪全.我国企业危机预警模型研究 —— 以财务与非财务因素构建[ J].金融研究,2006(2):78 ~ 87.
马若微,唐春阳.考虑误判损失的Logistic违约预测模型构建[ J].系统工程理论与实践,2007(8):33 ~ 38+98.
王春峰,万海晖,张维.商业银行信用风险评估及其实证研究[ J].管理科学学报,1998(1):68 ~ 72.
吴世农,陈智榆,吴育辉.机器学习预警模型能更有效预测债券违约风险吗?[Z].厦门大学管理学院工作论文,2021.
吴世农,黄世忠.企业破产的分析指标和预测模型[ J].中国经济问题,1987(6):8 ~ 15.
吴世农,卢贤义.我国上市公司财务困境的预测模型研究[ J].经济研究,2001(6):46 ~ 55+96.
张玲.财务危机预警分析判别模型[ J].数量经济技术经济研究,2000(3):49 ~ 51.
张友棠.财务预警系统管理研究[ J].财会通讯,2004(1):63 ~ 67.
Altman E. I., Brenner M.. Information Effects and Stock Market Response to Signs of Firm Deterioration[ J].Journal of Financial and Quantitative Analysis,1981(1):35 ~ 51.
Altman E. I.. Financial Ratio, Discriminant Analysis and the Prediction of Corporate Bankruptcy[ J].Journal of Finance,1968(9):589 ~ 609.
Beaver W.. Financial Ratios as Predictors of Failure[ J].Journal of Accounting Research,1966(4):71 ~ 111.
Duffie D., Lando D.. Term Structure of Credit Spreads with Incomplete Accounting Information[ J].Econometrica,2001(3):633 ~ 664.
Ohlson J. A.. Financial Ratios and Probabilistic Prediction of Bankruptcy[ J].Journal of Accounting Research,1980(18):109 ~ 131.
